墨水直写打印网格膜的润湿性研究*

田 伟，李木军

(中国科学技术大学 精密机械与精密仪器系，安徽 合肥 230026)

墨水直写技术是一种常见的材料挤出式3D打印方法，其制造的硅树脂网格膜具有超疏水性[1-2]。传统的超疏水结构制造方法通常都需要复杂的工艺步骤或者昂贵的模具，即便这样，其制造有序、复杂的微结构的能力仍然有限[3-4]。与这些传统方法不同的是，墨水直写技术方法简便，通用性强，不需要使用任何模具，并且只需一步就可以制造出有序多孔的超疏水网格膜，制造优势非常明显。3D打印的超疏水网格膜结合结构上的多孔性和硅树脂材料本身的亲油性可以应用到油水分离、防水透气等多个领域。通常情况下，超疏水网格膜是通过在金属网上覆盖超疏水涂层获得的。这样制备的超疏水网格膜主要存在2个问题：1)网孔不均匀；2)界面结合力差。网孔不均导致油水分离性能不稳定，而在金属网变形(弯曲、拉伸)的情况下，涂层非常容易脱落，从而丧失了超疏水性。与之相比，墨水直写制备的网格膜不存在这样的问题。由于3D打印技术控制性好，所以其制备的网格膜的网孔大小均一；并且由于是一步制造完成，无界面结合问题，变形后能自动恢复原状，仍保持超疏水性、机械稳定性和良好的耐用性。

墨水直写打印的超疏水网格膜上存在着亚毫米级和微纳米级的结构。亚毫米结构是指打印纤维及其形成的凹槽结构，其对网格膜的润湿性有重要影响，但是相关研究比较缺乏。本文通过调整亚毫米结构来改变网格膜的润湿性，从润湿理论的角度来分析亚毫米结构对网格膜润湿性的影响，对制备不同润湿性的网格膜具有一定的指导意义。

1 DIW制备网格膜

DIW打印技术的关键是设计粘弹性的墨水，其对墨水的流变性有2个基本要求：1)剪切变稀；2)自支撑[5-6]。剪切变稀是为了在挤压时使打印墨水粘度下降从喷嘴里顺利挤出；自支撑是为了让打印纤维从喷嘴挤出后有足够的剪切屈服应力保持形状而不坍塌。为了保证DIW打印网格膜的质量，首先需要配置合格的墨水。

1.1 打印墨水的配制

在试验中，硅树脂基础材料选用DragonSkin ® 10 Slow(Smooth-On公司)，它是一种双组份硅树脂，part A和part B按照质量比1∶1配制使用；液态增稠剂选用THI-VEX，适量添加能增加纯硅树脂墨水的粘度，改善打印性能；纳米颗粒选用疏水性纳米二氧化硅H260(阿拉丁公司)，粒径在7～40 nm范围内。

配置墨水时，首先将硅树脂的part A、part B和THI-VEX按照质量比100∶100∶0.5混合在一起，充分搅拌、脱泡，配制成基础墨水，然后在基础墨水里添加适量的纳米SiO2，充分搅拌、脱泡后就配制成含12wt%纳米SiO2的打印墨水。打印墨水配制好后，需要转移到30 mL的注射针筒内，再次脱泡后备用。

配制过程中所用的主要设备是电子分析天平(YT1003，乐祺公司)和行星式搅拌机(ARE-310，Thinky公司)。

1.2 网格膜的制备

网格膜的打印原理如图1所示，相邻两层纤维打印方向互相垂直，同层纤维互相平行，纤维间距指的是每层相邻两条纤维轴线之间的距离。

图1 网格膜的打印原理图

本文主要研究亚毫米结构对网格膜润湿性的影响。网格膜横截面示意图如图2所示，亚毫米结构主要有3个参数：纤维宽度、凹槽的宽度和深度。网格膜的纤维宽度约等于纤维直径，在试验中保持不变；通过改变纤维间距可以调整凹槽的宽度；通过叠加纤维能够增加凹槽的深度。为称呼方便，把未叠加纤维的网格膜称为S型网格膜，叠加纤维的网格膜称为D型网格膜。

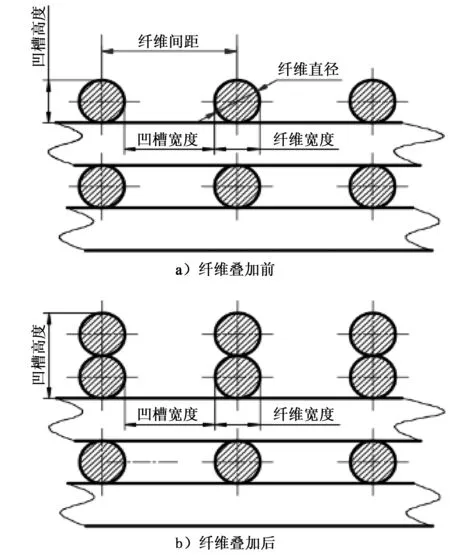
图2 网格膜横截面示意图

网格膜的打印参数确定如下：纤维直径均保持在(260±10) μm范围内，通过调整挤出压力来实现；纤维间距(filament space，FS)依次为0.6、0.7、0.8和0.9 mm；打印速度是600 mm/min；层厚是0.25 mm。网格膜相邻两层纤维方向互相垂直，S型网格膜打印4层；D型网格膜打印5层，后2层叠加。打印效果如图3所示。

图3 网格膜打印效果图

2 润湿性表征

对于疏水性表面而言，要考虑静态接触角和滚动角2个方面才能比较全面地描绘其润湿性[7]。网格膜的凹槽结构使其润湿性呈现各向异性；为了区分，作了如下规定：接触角测量时，当接触角的基线垂直于顶层纤维，此时测量的接触角称为垂直接触角；当接触角的基线平行于顶层纤维，此时测量的接触角称为平行接触角。滚动角测量时，当水滴沿着顶层纤维滚动，此时测量的滚动角称为平行滚动角；而当水滴垂直于顶层纤维滚动，此时测量的滚动角称为垂直滚动角。研究凹槽结构的垂直接触角和平行滚动角对其在润湿性方面的相关应用更有意义，因此本文主要研究墨水直写打印的亚毫米结构对垂直接触角和平行滚动角的影响，下文分别简称为接触角和滚动角。

润湿性表征所用的设备是水滴角测量仪(CA100C，上海盈诺精密仪器公司)。测量时，所用水滴体积是5 μL，需要在网格膜的不同位置测量5次，取其平均值作为有效值。需要注意的是：滚动角测量时，需要缓慢调节平台的角度，避免产生振动和惯性使水滴滚动。

2.1 静态接触角表征结果

S型和D型网格膜的接触角测量结果如图4所示。从图4中可以看出，2种网格膜的接触角变化规律相同：随着纤维间距增加，网格膜的接触角先增加后减小。在纤维间距是0.7和0.8 mm时，网格膜的接触角超过150°，此时的网格膜具有超疏水性。通过对比还发现，在纤维间距相同的情况下，2种网格膜的接触角几乎相同，凹槽深度对接触角几乎没有影响。

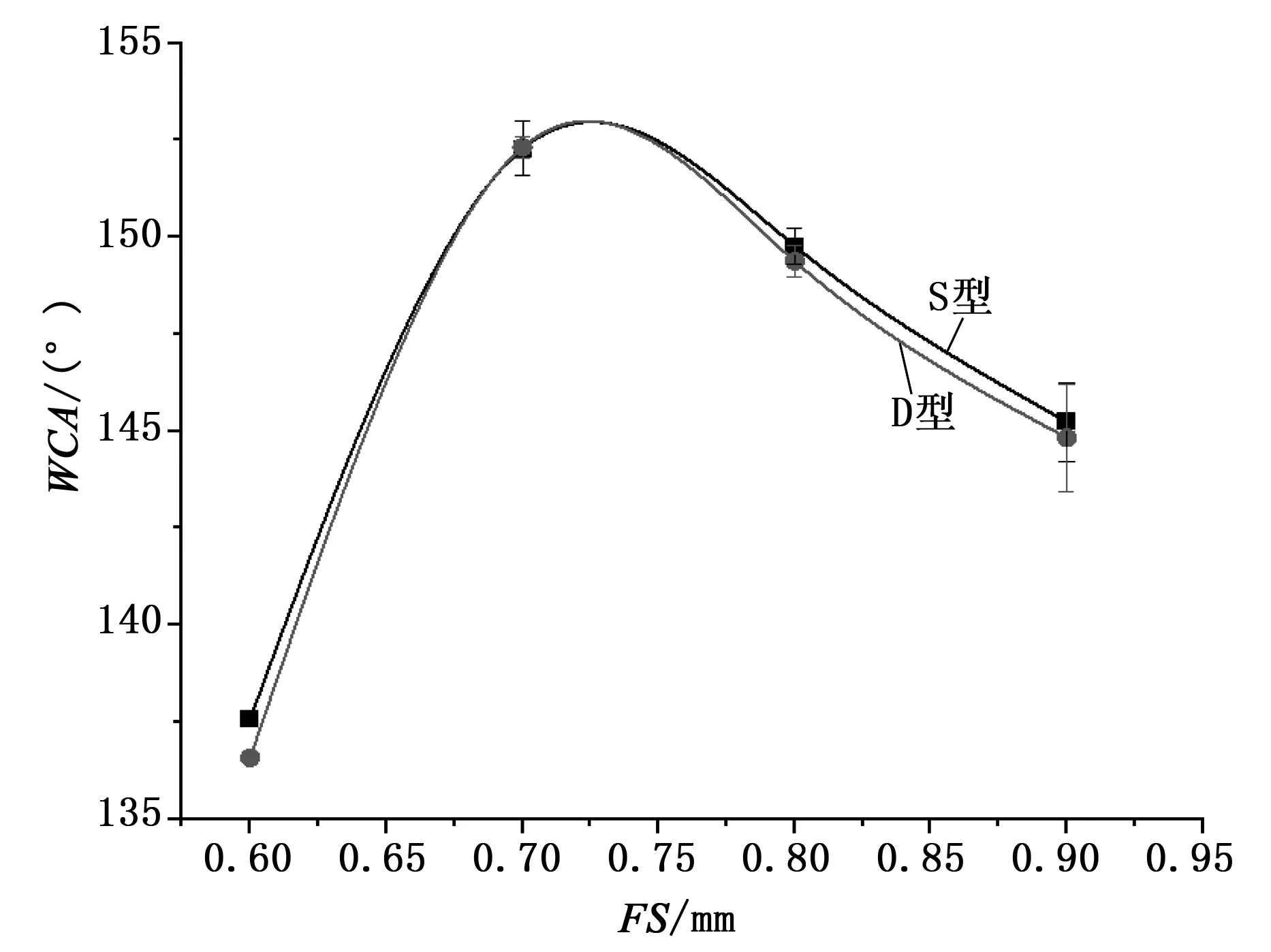
图4 网格膜的接触角与纤维间距关系

2.2 滚动角表征结果

测量S型网格膜的滚动角时，现象比较复杂。在纤维间距0.6 mm时，网格膜的滚动角约为48°。当纤维间距为0.7 mm时，水滴有时候能顺利滚完全程，有时候滚到一半停止滚动，有时候根本不滚动。当纤维间距为0.8和0.9 mm时，水滴基本不滚动。

D型网格膜的滚动角测量结果如图5所示。从图5中可以看到，随着纤维间距增加，滚动角先减小后增加。可见疏水性纳米SiO2的添加使滚动角增大。相比S型网格膜，D型网格膜的滚动特性稳定且有规律，位于其上的水滴不存在无法滚动的情况。

图5 D型网格膜的滚动角与纤维间距关系

3 亚毫米结构对润湿性的影响

3.1 亚毫米结构对接触角的影响

在纤维间距相同时，S型和D型网格膜的接触角几乎相同，但是二者的接触角测量图有着明显的差别(见图6)。当纤维间距为0.6和0.7 mm时，水滴的润湿状态相似；当纤维间距为0.8和0.9 mm时，水滴的润湿状态明显不同：在S型网格膜上，水滴充满整个凹槽，而在D型网格膜上，水滴与凹槽底部有明显缝隙。

图6 接触角测量图

Cassie在分析服装的润湿性时，将其简化为“圆柱纤维”进行分析[8](见图7)。

图7 水滴在“圆柱纤维”上

水滴在D型网格膜上的状态与水滴在服装上的状态相似，但是由于纤维直径尺寸和纤维间距差异大，水滴在D型网格膜上仅坐落在2～3根纤维上。为验证水滴在D型网格膜上处于Cassie状态，应用SolidWorks软件建模，模拟水滴在D型网格膜上的状态(见图8)。

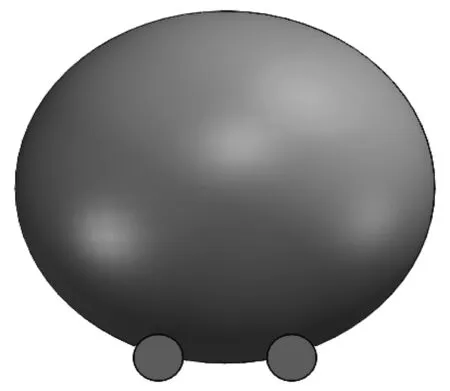
图8 模拟水滴状态(纤维间距0.7 mm)

根据Cassie润湿理论，Cassie-Baxter方程如下所示：

cosθr=f1cosθ1-f2

(1)

式中，θr是表观接触角；θ1是本征接触角；f1是平行于粗糙表面的单元几何表面上总的固液界面的面积；f2平行于粗糙表面的单元几何表面上总的气液界面的面积。用打印墨水制成平面，然后测量其接触角，在不同的位置测量5次，取平均值，得到θ1=122°。在SolidWorks软件里测量出固液界面面积、气液界面面积和几何平面面积，求出，然后利用Cassie方程计算接触角的理论值，并与试验测量值进行对比，结果见表1。

表1 D型网格膜接触角的计算值和测量值

从表1可以看出，接触角的计算值与测量值相差在1°～4°范围内且变化规律一致。这有力地说明了水滴在D型网格膜上处于Cassie润湿状态。

水滴在S型网格膜上的润湿状态则不确定。当纤维间距为0.6 mm时，水滴在S型网格膜上也处于Cassie状态。当纤维间距为0.7 mm时，水滴在S型网格膜上的润湿状态不稳定：在水滴润湿过程中，针头的扰动可能会使从Cassie状态变为Wenzel状态[9]。另外，水滴在滚动时会发生比较严重的变形，与凹槽底部接触，润湿状态由Cassie变为Wenzel。当纤维间距为0.8和0.9 mm时，水滴充满整个凹槽，明显处于Wenzel润湿状态。

当纤维间距为0.7、0.8和0.9 mm时，水滴在S型和D型网格膜上的润湿状态不同，但接触角近似相同。这极可能与水滴的润湿过程相关。水滴在网格膜上的润湿过程(见图9)与在平面上的润湿过程相反。在润湿平面时，水滴底部先与平面接触，然后三相接触线(three-phase contact line，TCL)慢慢向四周扩展，直至稳定；在润湿网格膜时，水滴最先与纤维接触，此时水滴的底部仍处于悬空状态，润湿快结束时，水滴底部才开始与凹槽底部接触，接着充满凹槽。也就是说水滴的大部分润湿过程发生在顶层纤维上，大部分固液界面位于顶层纤维上，面积很小。水滴底部与凹槽的接触面积相对较小，对f1、f2影响很小，所以接触角变化不大或几乎不变。

图9 水滴润湿S型网格膜

在纤维直径一定的情况下，网格膜的接触角随槽宽增加先变大后变小，槽深变化对接触角几乎没有影响。经过分析得出如下结论：在打印纤维直径一定的情况下，亚毫米结构的槽宽和槽深会影响水滴在网格膜上的润湿状态。当槽深足够深时，水滴处于Cassie状态，此时可以通过调整槽宽来改变接触角的大小。随着槽深减小，水滴会从槽宽大的网格膜开始，由Cassie状态逐渐过渡到Wenzel状态，但是由于槽深的影响，接触角几乎保持不变。

3.2 亚毫米结构对滚动角的影响

Masashi Miwa等证明：在使水滴处于Cassie状态的高度疏水表面上，接触角越大滚动角越小，二者变化规律相反[10]。在3.1小节里，笔者利用Cassie方程证明了亚豪米结构使水滴在D型网格膜上处于Cassie状态。而从图5可以发现，D型网格膜的平行滚动角随纤维间距增加先减小后增大，与接触角的变化规律正好相反。这与Masashi Miwa等的研究结论一致。

S型网格膜的平行滚动角与水滴的润湿状态密切相关。纤维间距相同时，S型网格膜的垂直接触角与D型网格膜的几乎相同，但是由于亚毫米结构的槽深不够，水滴的润湿状态不完全一致，这导致了平行滚动角的差异。下述根据润湿状态分析S型网格膜的滚动特性。

1)Cassie状态。

图6中，当纤维间距为0.6 mm时，水滴在S型网格膜上润湿状态与在D型网格膜上的一样，均处于Cassie状态，所以平行滚动角与D型网格膜的几乎相等。

2)Wenzel状态。

图6a中，当纤维间距为0.8和0.9 mm时，水滴在S型网格膜上处于Wenzel润湿状态，水滴不滚动，即平行滚动角α=90°，比D型网格膜的平行滚动角大50°～60°。修正的Furmidge方程可用于计算平行沟槽结构的平行滚动角[11]，如下所示：

(2)

式中，α是滚动角；m是水滴质量；g是重力加速度；W是固液界面的实际宽度；YLG是液气表面张力；θR是后退接触角；θA是前进接触角。对同样体积的水滴而言，滚动角主要由固液界面的实际宽度和接触角滞后决定。

水滴的三相接触线如图10所示。

水滴在网格膜上的润湿状态会影响固液界面的实际宽度，对Cassie水滴而言：

w=2w1

(3)

对Wenzel水滴而言：

w=2w1+w2+2h

(4)

式中，h为凹槽的深度。

可见，Wenzel水滴的w显著增加。当要使水滴滚动距离时，Wenzel水滴的润湿面积变化量比Cassie水滴的要多2(w2+2h)dl，甚至比Cassie水滴的润湿面积变化量2w1dl还大。因为水滴滚动时消耗的能量与润湿面积变化量成正比，因此Wenzel水滴比Cassie水滴的滚动难度增加数倍。除此之外，由于状态不同，Cassie水滴在滚动方向上没有润湿能量势垒，而Wenzel水滴在滚动方向有润湿能量势垒，这就使得Wenzel水滴的接触角滞后会明显大于Cassie水滴[12]。由于Wenzel水滴固液界面实际宽度和接触角滞后都明显大于Cassie水滴，所以其平行滚动角会明显大于Cassie水滴。

图10 水滴的三相接触线

3)不稳定状态。

当纤维间距为0.7 mm时，水滴在S型网格膜上的润湿状态不稳定，这造成了滚动特性的不稳定。接触角和滚动角测量时，外界的扰动都可能使水滴从Cassie状态转变为Wenzel状态，使水滴的滚动特性发生改变。

在纤维直径一定的情况下，通过调整亚毫米结构的槽宽和槽深能改变水滴的润湿状态：当水滴处于Wenzel状态时，水滴不滚动，这是由于水滴的接触角滞后和固液界面实际宽度增加导致粘附力增加；当水滴处于Cassie状态时，由于水滴的接触角滞后和固液界面实际宽度都减小导致粘附力减小，水滴可以滚动，此时调节亚毫米结构的槽宽可以有效改变滚动角的大小。

4 结语

在纤维直径一定的情况下，通过调整亚毫米结构的槽宽和槽深来改变DIW打印的网格膜的润湿性，根据润湿性理论和表征结果，深度解析亚毫米结构对网格膜润湿性的影响。在研究中发现，亚毫米结构决定水滴的润湿状态：在槽深足够的前提下，水滴处于Cassie状态，这时通过调整纤维间距来改变槽宽，进而调整网格膜的接触角。随着槽深降低，从槽宽大的网格膜开始，水滴会从Cassie状态慢慢过渡到Wenzel状态。通过调整亚毫米结构能够改变水滴的润湿状态，控制水滴是否能够滚动：Wenzel水滴无法滚动，Cassie水滴能够滚动。对于Cassie水滴，通过调整亚毫米结构的槽宽，能够改变滚动角的大小。