基于超弹性本构模型的双脉冲发动机径向软隔层承载数值研究

王 鼎，吴 昊，白玉冰，迟 雪，3，朱 力，3

(1.海军装备部驻西安地区军事代表局，陕西 西安 710000；2.中国航天科工集团六院四十一所，内蒙古 呼和浩特 010010；3.国防科技大学 空天科学学院，湖南 长沙 410000)

脉冲发动机利用隔离装置将固体火箭发动机的燃烧室分成若干部分，可进行多次的关机和启动，合理分配推力及各脉冲间隔时间，实现导弹飞行弹道的最优控制和发动机能量的最优管理[1]。采用脉冲发动机的导弹具有高速、远射程、高命中率和较轻的系统结构质量等特点[2]，在实际应用中，双脉冲固体火箭发动机不仅能明显提升性能，又不会过度提升设计复杂性和大幅降低系统可靠性[3]。

双脉冲发动机燃烧室内2个药柱由隔离装置间隔开。在一脉冲工作时，隔离装置起到隔离高温燃气的作用，避免二脉冲药柱受热燃烧，此外隔离装置还要承受燃烧室内高压燃气作用，保持自身结构完整性。对于软隔层结构的双脉冲发动机，一脉冲工作时，软隔层受到高温高压燃气作用，会产生较大的变形，与二脉冲药柱接触贴合，若隔层结构设计不合理会导致结构破坏，隔离失效，造成二脉冲药柱提前燃烧工作，燃烧室内压强快速升高，最终导致发动机壳体超压破坏，工作失利。

本文主要研究对象为双脉冲发动机软隔层，根据双脉冲发动机工作过程中径向软隔层大变形、高弹性、小应变的特点，以实测的橡胶材料、推进剂性能数据为基础，采用超弹性本构模型对隔层三元乙丙橡胶材料以及推进剂材料性能进行表征；对一脉冲工作时二脉冲药柱、隔层间隙工况下的软隔层受力情况，应用Abaqus软件进行数值模拟，获得隔层的实际应变情况，结合实际发动机研制基础，为后续双脉冲发动机软隔层设计及优化指出方向。

1 材料参数确定

1.1 橡胶本构及参数确定

本文中双脉冲发动机所用隔离装置为橡胶软隔层，在加载过程中具有大变形、高弹性的性质[4]。对于橡胶材料，常用的本构模型有Mooney-Rivlin模型和Odgen模型。

Mooney-Rivlin模型能很好地体现橡胶材料在中等应变情况下方位应变能，由于结构简单，在超弹性本构计算中被广泛应用[5]，其应变能函数如下：

(1)

式中，C、d为材料常数，由材料试验确定；I1、I2为变形张量；J为体积率，橡胶是不可压缩的，故取J=1。

通过应变能函数对主伸长比λ求导，并根据不可压缩材料单轴拉伸条件可得

(2)

式中，t为单轴拉伸应力；λ为主伸长比。

D=C10+C01E

(3)

Odgen模型由Odgen于1972年提出，是将主伸长比λi作为应变能函数自变量的新的应变能函数。Odgen应变能函数定义为

(4)

式中，μn和αn为材料常数；K为初始体积模量。

通过应变能函数对主伸长比求导，并根据不可压缩材料单轴拉伸条件可得

(5)

进一步可得基于Odgen模型的单轴拉伸应力表达式为

(6)

分别采用M-R模型和Odgen模型对橡胶标准试件500 mm/min拉伸速率单项拉伸试验数据进行拟合，超弹性本构模型力与位移曲线如图1所示，本构特性参数见表1和表2。

图1 本构拟合曲线

表1 M-R模型参数

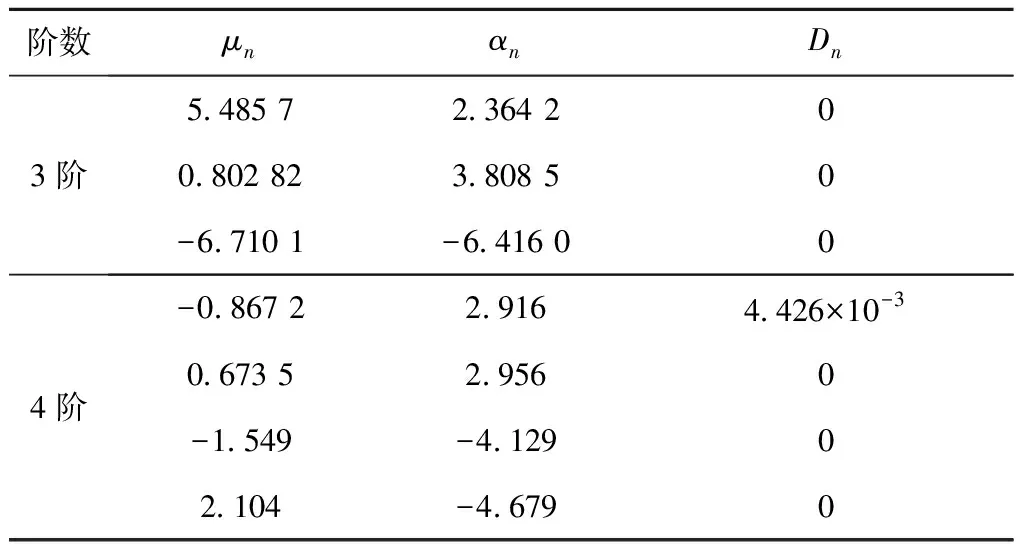
表2 Odgen模型参数

由图1可看出，相比Mooney-Rivilin模型，Odgen模型与材料拉伸曲线贴合度更好，能更准确地反应隔层弹性材料性能，且随着参数数量的提升，4阶Odgen模型比3阶模型具有更高的精度，因此本文中采用4阶Odgen模型进行隔层结构受力分析。

1.2 推进剂参数确定

材料变形的应变能(或变形能)是在外载荷的作用下发生变形，研究表明，储存在材料中的能量，应变能函数能较好表征物体的变形特征，在超弹性材料中，常用的应变能模型有描述橡胶变形行为的Mooney-Rivlin模型、Odgen模型等及描述生物薄膜变形行为的Fung模型、GPR模型等。

固体推进剂是典型的粘超弹性材料，在许多实际应用中，其力学行为表现出明显的非线性。为了准确表征推进剂在有限变形条件下的力学性能，对推进剂的本构模型进行研究。由于推进剂在单向拉伸条件下应力应变曲线与橡胶类材料拉伸响应曲线形状相近，本文考虑以橡胶类材料的应变能表达式作为函数模型来描述推进剂的拉伸变形。固体推进剂单向拉伸应力应变曲线如图2所示，拟合推进剂本构特性参数见表3。

图2 固体推进剂应力应变曲线

表3 推进剂本构模型参数

2 计算实例

2.1 有限元分析前处理

为了简化计算，提高计算速度与精度，本次计算采用二维轴对称模型，仅对二脉冲侧结构进行分析，整个模型由燃烧室壳体、二脉冲药柱、绝热层、隔层和顶盖组成，重点研究隔层在一脉冲工作过程中承载变形的应力应变。为减轻沙漏效应，隔层与药柱采用轴对称杂交缩减积分网格CAX4RH，其余结构采用轴对称缩减积分网格CAX4R[6]。发动机直径R，二脉冲药柱长度3.5R，隔层厚度取0.06R，对隔层与药柱取2、4和6 mm的不同径向间隙进行分析，发动机轴对称模型如图3所示。

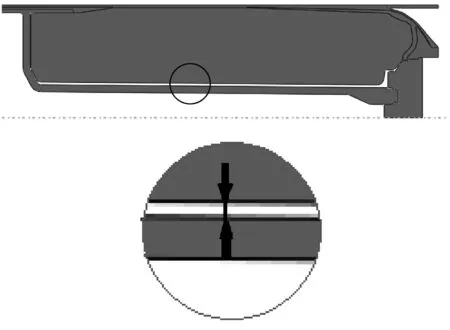
图3 有限元分析建模

在双脉冲发动机一脉冲工作时，隔层承受一脉冲工作高压燃气作用，会产生较大变形，与二脉冲药柱贴合[7]。由于隔层头部与顶盖连接、大端与壳体粘接，变形受到约束，理论分析隔层承载会在筒段产生较大的环向和径向应变，轴向应变相对较小，因此分析主要针对隔层的筒段部位[8]。

隔层变形后与药柱接触，存在一定的摩擦因数，本次计算中对隔层与药柱接触摩擦因数取0.15[9]。发动机前裙施加固定约束，对隔层与壳体粘接处采用绑定约束[10]。在分析过程中对隔层施加法向的压力，载荷采用3个分析步进行施加，以利于隔层和药柱建立平稳接触，加载曲线如图4所示。

图4 加载曲线

2.2 有限元分析结果

2.2.1 2 mm径向间隙计算结果

图5所示为内压载荷下隔层整体径向应变，由图5可知，隔层大端承受拉应力，应变最大值为2.02%，位于锥段与筒段转折位置；隔层筒段整体承受压应力，应变最大值为15.44%，位于隔层头部，筒段中部位置应变值为12.62%。

图5 隔层整体径向应变

图6所示为内压载荷下隔层整体轴向应变，由图6可知，隔层整体应变水平较低，在隔层锥段与筒段转折位置应变水平较大，既存在拉应力也存在压应力，拉应力最大应变为10.61%，压应力最大应变为7.64%，筒段中部位置应变值为0.63%。

图6 隔层整体轴向应变

图7所示为内压载荷下隔层整体环向应变，由图7可知，隔层筒段承受拉应力，应变最大值为13.48%，位于筒段靠近头部位置，筒段中部位置应变值为10.87%。

图7 隔层整体环向应变

2.2.2 4 mm径向间隙计算结果

图8所示为内压载荷下隔层整体径向应变，由图8可知，隔层大端承受拉应力，应变最大值为5.07%，位于锥段与筒段转折位置；隔层筒段整体承受压应力，应变最大值为23.39%，位于隔层头部，筒段中部位置应变值为17.21%。

图8 隔层整体径向应变

图9所示为内压载荷下隔层整体轴向应变，由图9可知，隔层整体应变水平较低，在隔层锥段与筒段转折位置应变水平较大，既存在拉应力也存在压应力，拉应力最大应变为17.16%，压应力最大应变为13.5%，筒段中部位置应变值为1.12%。

图9 隔层整体轴向应变

图10所示为内压载荷下隔层整体环向应变，由图10可知，隔层筒段承受拉应力，应变最大值为19.16%，位于筒段靠近头部位置，筒段中部位置应变值为16.94%。

图10 隔层整体环向应变

2.2.3 6 mm径向间隙计算结果

图11所示为内压载荷下隔层整体径向应变，由图11可知，隔层大端承受拉应力，应变最大值为8.24%，位于锥段与筒段转折位置；隔层筒段整体承受压应力，应变最大值为32.0%，位于隔层头部，筒段中部位置应变值为22.4%。

图12所示为内压载荷下隔层整体轴向应变，由

图11 隔层整体径向应变

图12可知，隔层整体应变水平较低，在隔层锥段与筒段转折位置应变水平较大，既存在拉应力也存在压应力，拉应力最大应变为20.81%，压应力最大应变为18.60%，筒段中部位置应变值为1.85%。

图12 隔层整体轴向应变

图13所示为内压载荷下隔层整体环向应变，由图13可知，隔层筒段承受拉应力，应变最大值为24.72%，位于筒段靠近头部位置，筒段中部位置应变值为21.88%。

图13 隔层整体环向应变

2.3 结果对比分析

将隔层与药柱径向3种间隙距离获得应变结果进行对比分析，3个方向应变值见表4。通过对隔层承载应力应变进行数值模拟并进行结果对比，可以得出如下结论。

1)隔层锥段与筒段转折处、隔层筒段头部应变水平较高，对于径向软隔层双脉冲发动机，该位置是发动机设计关键位置，需要优化结构以降低整体应变水平。

2)径向软隔层轴向整体应变水平较低；径向方向上隔层与药柱相互挤压，主要承受压应力，对应为压缩应变。

3)隔层整体受力水平与隔层、药柱间隙呈正相关，间隙越小，隔层受力水平越小。

4)隔层在一脉冲工作时承载应变水平远小于材料的极限延伸率(≥300%)，与实际试验中隔层破坏现象存在矛盾，说明隔层在达到强度极限前已经失效。

表4 加载后隔层三向应变值

3 结语

通过上述研究可以得出如下结论。

1)通过对一脉冲工作时隔层受力情况进行有限元分析，认为隔层筒段头部以及锥段与筒段转折处是结构的薄弱点，需要进行优化设计以降低隔层应变水平。

2)通过有限元分析，并结合实际试验中出现问题，说明隔层在应变远小于材料的极限时已经失效，表明现有的以最大延伸率作为材料承载极限的安全判据不适用。

3)分析不同二脉冲药柱、隔层间隙下隔层的应变变化情况，发现隔层受力水平与间隙呈正相关，减小药柱与隔层间隙可降低隔层应变水平。