基于UG的工业机器人圆弧插补后处理算法研究

王嘉翀，郭恩澍，李宏伟

(北京航星机器制造有限公司，北京 100010)

随着数控加工技术的不断发展，UG等CAD软件在数字化制造中起着越来越重要的作用[1]。当前通用CAD/CAM软件主要应用于数控机床的加工制造中，而对于工业机器人，一方面由于形成刀位轨迹逻辑的差异，另一方面由于缺乏对应的后置处理算法支持，使得其在工业机器人应用极为有限。通过分析二者的差异，发现除了语言指令的差别，在插补算法中特别是圆弧插补算法也存在较大的差异，工业机器人常用三点法圆弧插补指令，故研究一种将数控圆弧插补指令转换为工业机器人可利用的空间圆弧插补指令的算法，具有重要的应用意义。

空间圆弧曲线插补可以使数控系统可以直接加工各种圆弧[2]。陈汉军等[3]提出了一种根据给定精度利用圆弧逼近平面任意曲线的方法，为解决空间任意曲线插补提供了解决办法，但其利用点的离散化和曲率半径的算法并不适用于UG轨迹所提供的参数信息。裴世聪[4]对基于坐标系变换的空间任意圆弧插补算法进行了分析，但其主要是针对圆弧点的增量进行求解，而未对具体点值进行深入研究。赵燕伟、郭吉昌等[5-6]提出了基于UG加工信息进行工业机器人的轨迹规划，但未对运动的插补算法进行具体的研究。此外，还有其他学者[7-9]针对工业机器人的运动插补算法进行分析及优化，并实现了运动轨迹仿真，但只是针对路径规划角度的优化，并未对后置处理算法程序开展进一步的研究。

本文以UG后置处理中可获得的变量参数为基础，基于齐次变换矩阵方法研究了工业机器人的三点圆弧插补算法，并基于UG后置处理器进行了适用于工业机器人语言规则的程序开发及验证。

1 工业机器人的三点圆弧插补算法

工业机器人的空间圆弧指令是通过给定起点、中点、终点，从而确定一段圆弧曲线。而数控机床代码则是利用R或IJK模式实现。针对这个编码差异，笔者利用UG中圆弧指令可提供的参数，包括起点、终点、旋转角度以及圆轴矢量等，进行从二维平面到三维空间的递进圆弧插补算法转换和研究。

1.1 二维平面三点圆弧插补算法

在二维平面中，设O点坐标为(x0,y0)，A点坐标为(x1,y1)，中点C点坐标为(x,y)，旋转角度为θ，半径为r。由于圆轴矢量为固定值，因此求C点的坐标有如下2种方式。

1)复数域法。根据复数的定义公式求得：

x=a+(x0-a)cosα-(y0-b)sinα

y=b+(x0-a)sinα+(y0-b)cosα

2)向量法。

OA向量为：

OC向量为：

OC与OA向量的模均为：

|OC|=|OA|=r

(1)

OC与OA的夹角为θ，则有：

(2)

由式1和式2可求得坐标值X、Y。

对比验证见表1。

表1 2种算法对比结论

1.2 三维空间三点圆弧插补算法

在分析了二维平面的相关算法后，由于空间圆轴矢量的变化，使得矢量法求解极为复杂，但如果先基于二维平面的中点算法求出相对坐标系下的中点值，再结合三维空间的齐次坐标变换思路，解出基坐标系下的中点坐标，就为空间圆弧中点的求解提供了方法。空间圆弧中点图如图1所示。

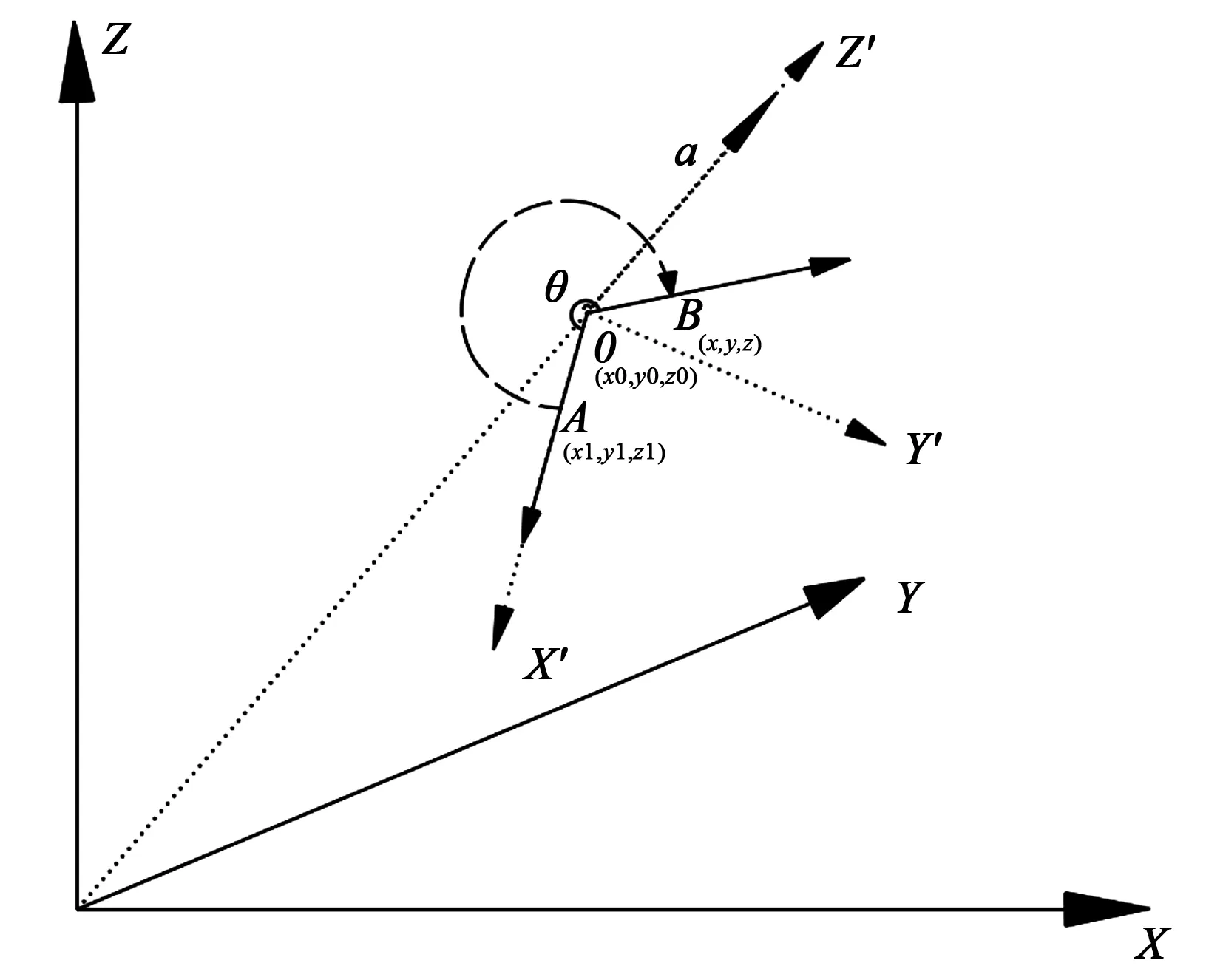
图1 空间圆弧中点图

图1中，假定已知圆轴矢量为a(ax,ay,az)，起点为A(x1,y1,z1)，终点为B(x,y,z)，圆心O为(x0,y0,z0)，旋转弧度为θ，XYZ为基坐标系，X′Y′Z′为圆弧平面坐标系，已知圆半径r，算法如下。

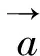
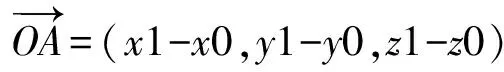
根据右手螺旋法则，Y′轴方向为：

(3)

相对坐标系X′Y′Z′与基坐标系XYZ的旋转变换矩阵为(需单位向量)：

(4)

在X′Y′Z′坐标系中，圆弧面在平面X′O′Y′上，则中点B坐标可描述为：

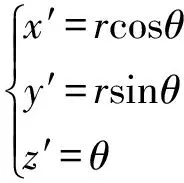
(5)

下一步需要将B点坐标转换至基坐标系XYZ下，利用坐标齐次变换，有：

(6)

将式3～式5代入式6并展开，则有

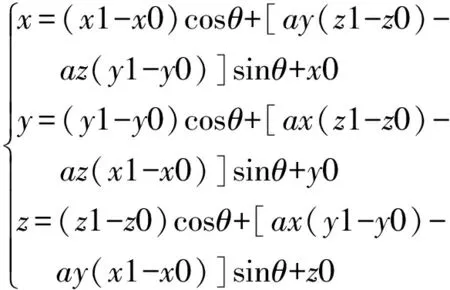
至此，已经可以求得空间圆弧中点一般算法公式，但在验证过程中发现一个问题，就是未将建立新建坐标系中X轴方向和所在圆弧的圆心位置圆轴矢量的垂直关系进行约束，可能导致圆弧面不垂直圆轴矢量的情况。故需要引入约束条件，直接建立圆轴矢量与X、Y方向的平面方程，引入X轴同Z轴垂直的约束条件，设(xp,yp,zp)为圆轴矢量恒通过的一点：

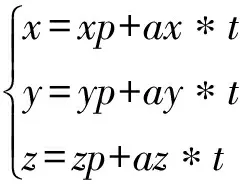
(7)

圆弧所在平面的法向量平面方程为：

ax*(x-x1)+ay*(y-y1)+
az*(z-z1)=0

(8)

那么联立式7和式8可确定圆心所在点的坐标参数t0：

t0=ax*(x1-xp)+ay*(y1-yp)+
az*(z1-zp)

(9)

将t0代入式10可得约束后圆心坐标为：

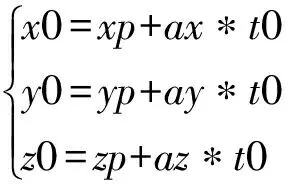
(10)

将式10代入式6，同时默认矢量恒通过已知圆心点，即可得到空间圆弧三点插补算法的求值函数：

式中，C=ax*x0+ay*y0+az*z0；K=1-cosθ。

2 基于UG的后置处理算法程序开发

在得到空间三点法圆弧取值算法后，需要在UG后置处理程序中进行相关程序的开发[10]，开发过程如下。

1)确定可获取变量信息，将UG/post中可获取的mom变量进行获取

global mom_arc_angle圆弧度数

set angle mom_arc_angle

……

2)算法程序编程，对旋转方向进行判定并引入算法函数(见图2a)。

判断旋转方向确定角度符号

if {[string match dir "clw"]} {set theta [expr angle/2*(-1)]

……

} else {set theta [expr angle/2*(-1)] }

参数值引入

set theta [expr theta*DEG2RAD]

……

set x_n [expr (a…)]

……

上述x_n,y_n,z_n即为求取的数值。

3)对后置处理变量信息进行替换输出变量(见图2b)。

首先在UG后置处理圆弧运动事件中，移取机床自带的G代码形式，重新定义三点的变量名称，再以ABB机器人圆弧插补指令格式进行格式转换和变量替换并输出。

工业机器人圆弧插补基本格式：

MoveL point{X,Y,Z}

MoveC Cirpoint{X,Y,Z},Topoint{X,Y,Z},speed[v]…

操作过程：在UG/post Builder中新建圆弧中点变量，在circle move事件中，先插入上述算法定制命令，再按照工业机器人基本指令格式引入变量参数并输出。

3 仿真验证

3.1 运动仿真验证

1)应用MATLAB软件对算法程序生成点位的算法进行验证，分别确认引入约束条件前和引入约束后旋转点位准确性。同时通过余弦公式对生成点位的转角进行反求验证。

a) 定制命令编程

b) 圆弧插补指令格式

约束前后点位图如图3所示，以(1,1,2)为圆轴矢量，点(1,1,2)为圆心，点(2,2,1)为起点，以10°为转角旋转1周，图4所示为以约束后算法旋转3/4周并生成10个点位。

图3 约束前后点位图

图4 算法点位图

验证结果：a.根据图3可知，约束前旋转平面与旋转矢量发生倾斜，通过计算旋转点与圆心连线的矢量与圆轴矢量的夹角，约束前旋转平面同圆轴矢量存在倾斜，约束后旋转平面与圆轴矢量为垂直关系，算法正确；b.图4中，输出各点坐标，通过空间余弦公式，计算得到相邻点转角为27°，验证正确。

2)应用MATLAB软件建立工业机器人模型，并对算法程序进行函数编程用于生成点位信息，进行仿真运动用于对圆弧轨迹进行确认。

a.对算法进行编程，建立ThreePoint2Circle.m算法函数，对起点、终点坐标点位进行换算，并固定圆轴矢量为(0,1,0)，圆心为点(0,0,0)。

b.建立工业机器人模型，并确定50个采样点进行仿真运动(见图5)。

图5 MATLAB算法建模及编程

验证结果：工业机器人模型根据该算法得到的点位信息可正确输出圆弧插补曲线(见图6)。

图6 工业机器人圆弧插补模拟

3.2 UG后置处理程序结果验证

该算法最终结论要应用于基于UG的后置处理程序中，需进行相关程序的加工编程并输出后置处理程序验证。

1)确定加工零件并对工件进行圆弧段加工编程(见图7)。

2)利用上述修改后后置处理器输出程序，并确认结果。

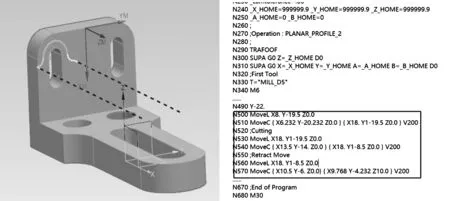
图7 UG后置处理程序结果示意图

图7中，UG加工模拟中存在进退刀和切削两部分圆弧运动，对比后置处理程序，存在进退刀和切削两部分圆弧插补指令，并符合工业机器人编码规则，同时提取点位信息进行验算，结果表明，生成三点信息满足对应圆弧段起点、中点、终点相关坐标，该算法可正确应用于UG后置处理程序。

4 结语

通过上述研究可以得出如下结论。

1)通过对圆弧插补指令的差异及原理进行分析，基于齐次变换矩阵的思路，研究了空间圆弧三点插补算法，对算法进行了约束优化，并经MATLAB仿真验证算法无误。

2)基于UG/post builder，将推导得到的空间算法进行编程嵌入，成功开发了由UG CAM得到的圆弧轨迹输出符合工业机器人的圆弧插补算法指令的后置处理程序，为进一步开发基于UG的工业机器人后置处理器提供算法基础。