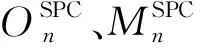若干类芳香族化合物的改良Sombor指数
黄宇飞, 刘合超
(1. 广州民航职业技术学院人文社科学院数学教学部, 广州 510403; 2. 华南师范大学数学科学学院, 广州 510631)
化学图论是一门将化学与图论相结合的交叉学科. 拓扑指数作为图的不变量,可用来预测有机化合物的物理化学性质,在化学和医药科学中具有重要的作用[1]. 众所周知,自化学图论发展至今已诞生了很多有价值的拓扑指数. 最近,GUTMAN和KULL提出了Sombor指数族的若干概念 (普通Sombor指数[2]、约化Sombor指数[2]和改良Sombor指数[3]等),经检验,它们在模拟烷烃的熵和蒸发焓方面显示出良好的预测和判别能力[4],这些描述可以成功地应用于化合物热力学性质的模拟,具有重要的化学应用价值.

1 预备知识


命题1设G是一个n阶连通简单图,则
根据命题1,易得如下2个推论:
推论1设G是连通简单图且其仅有(2,2)-型、(2,3)-型和(3,3)-型边,则
推论2设G是连通简单图且其仅有(2,2)-型、(2,4)-型和(4,4)-型边,则
2 4类芳香族化合物的改良Sombor指数的极值与极图
2.1 随机苯链


图1 苯链的3种局域排布
随机苯链(族)HXG(n;p1,p2)是指通过逐步添加末端苯环并最终形成由n(≥2)个苯环构成的苯链,其中第t(t=3,4,…,n)步添加末端苯环时有以下3种随机情形:
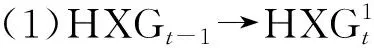
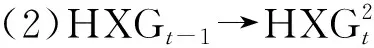




下面将刻画随机苯链HXG(n;p1,p2)的改良Sombor指数的数学期望.

证明根据随机苯链的结构,易见其是连通简单图且其仅有(2,2)-型、(2,3)-型和(3,3)-型边. 由推论1可得:
当n≥3时,注意到末端的苯环有3种连接方式(图1),故可考虑分析以下3种情形.

m22(G1)=m22(G)+1,
m23(G1)=m23(G)+2,
m33(G1)=m33(G)+2,
所以,结合推论1可得:

m22(G2)=m22(G)+0,
m23(G2)=m23(G)+4,
m33(G2)=m33(G)+1,
所以,结合推论1可得:

m22(G3)=m22(G)+1,
m23(G3)=m23(G)+2,
m33(G3)=m33(G)+2,
所以,结合推论1可得:
综上可得:
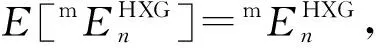
即得所需结论. 证毕.
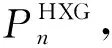
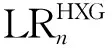
下面将给出随机苯链的改良Sombor指数的极值与极图刻画.

证明根据定理1可知:

由于

所有由n个苯环构成的随机苯链的改良Sombor指数的均值可表示为:
由于HXGn中每个元具有相同的发生概率,故有p1=p2=1-p1-p2=1/3,从而由定理1可得如下结论:



2.2 随机聚苯链

随机聚苯链(族)PPC(n;p1,p2)是指通过逐步添加末端割边及苯环并最终形成由n(≥2)个苯环及n-1条割边构成的聚苯链,其中第t(t=3,4,…,n)步添加末端苯环有以下3种随机情形:
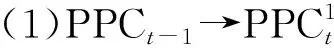





下面将刻画随机聚苯链PPC(n;p1,p2)的改良Sombor指数的数学期望.
定理4随机聚苯链PPC(n;p1,p2)的改良Sombor指数的数学期望为:
证明根据随机聚苯链的结构,易见其是连通简单图且其仅有(2,2)-型、(2,3)-型和(3,3)-型边. 由推论1可得:
当n≥3时,注意到末端的割边及苯环有3种连接方式(图2),故可考虑分析以下3种情形.

图2 聚苯链的3种局域排布

m22(G1)=m22(G)+2,
m23(G1)=m23(G)+4,
m33(G1)=m33(G)+1,
所以,结合推论1可得:

m22(G2)=m22(G)+3,
m23(G2)=m23(G)+2,
m33(G2)=m33(G)+2,
所以,结合推论1可得:

m22(G3)=m22(G)+2,
m23(G3)=m23(G)+4,
m33(G3)=m33(G)+1,
所以,结合推论1可得:
综上可得:

即得所需结论. 证毕.

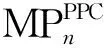
下面将给出随机聚苯链的改良Sombor指数的极值与极图刻画.

证明根据定理4可知:

由于
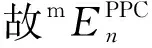
所有由n个苯环和n-1条割边构成的随机聚苯链的改良Sombor指数的均值可记为:
由于PPCn中每个元具有相同的发生概率,故有p1=p2=1-p1-p2=1/3,从而由定理4可得如下结论:
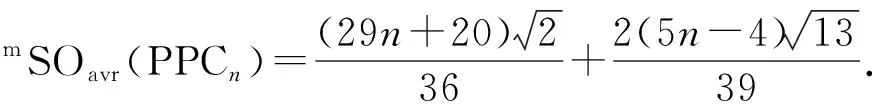


2.3 随机亚苯基链


图3 亚苯基链的3种局域排布
随机亚苯基链(族)RPH(n;p1,p2)是指通过逐步添加末端环丁烷及苯环并最终形成由n(≥2)个苯环和n-1个环丁烷构成的亚苯基链,其中第t(t=3,4,…,n)步添加末端苯环有以下3种随机情形:





下面将刻画随机亚苯基链RPH(n;p1,p2)的改良Sombor指数的数学期望.
定理7随机亚苯基链RPH(n;p1,p2)的改良Sombor指数的数学期望为
证明根据随机亚苯基链的结构,其是连通简单图且其仅有(2,2)-型、(2,3)-型和(3,3)-型边. 由推论1可得:
当n≥3时,注意到末端的环丁烷及苯环有3种连接方式(图3),故可考虑分析以下3种情形.

m22(G1)=m22(G)+1,
m23(G1)=m23(G)+2,
m33(G1)=m33(G)+5,
所以,结合推论1可得:

m22(G2)=m22(G)+0,
m23(G2)=m23(G)+4,
m33(G2)=m33(G)+4,
所以,结合推论1可得:

m22(G3)=m22(G)+1,
m23(G3)=m23(G)+2,
m33(G3)=m33(G)+5,
所以,结合推论1可得:
综上可得:
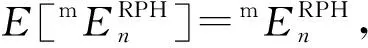
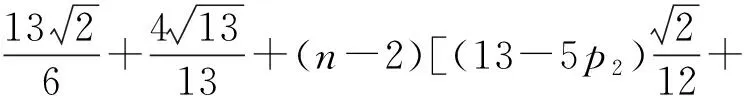
即得所需结论. 证毕.


下面将给出随机亚苯基链的改良Sombor指数的极值与极图刻画.

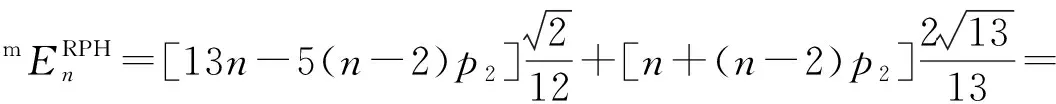
由于

所有n个苯环构成的随机亚苯基链的改良Sombor指数的均值可表示为:
由于RPHn中每个元具有相同的发生概率,故有p1=p2=1-p1-p2=1/3,从而由定理7可得如下结论:
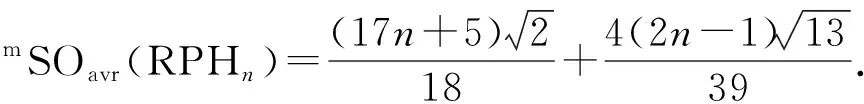


2.4 随机斯皮罗链

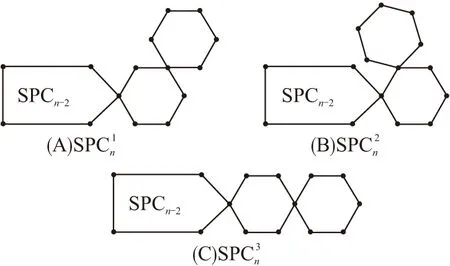
图4 斯皮罗链的3种局域排布
随机斯皮罗链(族)SPC(n;p1,p2)是指通过逐步添加末端苯环并最终形成由n(≥2)个苯环构成的斯皮罗链,其中第t(t=3,4,…,n)步添加末端苯环有以下3种随机情形:






下面将刻画随机斯皮罗链SPC(n;p1,p2)的改良Sombor指数的数学期望.
定理10随机斯皮罗链SPC(n;p1,p2)的改良Sombor指数的数学期望为:
证明由随机斯皮罗链的结构可知其是连通简单图且仅有(2,2)-型、(2,4)-型和(4,4)-型边. 由推论2可得:
当n≥3时,注意到末端苯环有3种连接方式(图4),故可考虑分析以下3种情形.

m22(G1)=m22(G)+2,
m24(G1)=m24(G)+4,
m44(G1)=m44(G)+0,
所以,结合推论2可得:

m22(G2)=m22(G)+3,
m24(G2)=m24(G)+2,
m44(G2)=m44(G)+1,
所以,结合推论2可得:

m22(G3)=m22(G)+2,
m24(G3)=m24(G)+4,
m44(G3)=m44(G)+0,
所以,结合推论2可得:
综上可得:

即得所需结论. 证毕.

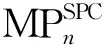
下面将给出随机斯皮罗链的改良Sombor指数的极值与极图刻画.

证明由定理10可知:
由于

所有由n个苯环构成的随机斯皮罗链的改良Sombor指数的均值可记为:
由于SPCn中每个元具有相同的发生概率,故有p1=p2=1-p1-p2=1/3,从而由定理10可得如下结论:
定理12SPCn中所有元的改良Sombor指数的均值为: