复合材料机身帽型长桁加筋壁板压缩屈曲及失效特性研究

李真，程立平

（1.上海飞机设计研究院飞机结构强度工程技术所，上海201210）

（2.中国飞机强度研究所复合材料结构强度研究室，西安710065）

0 引 言

先进碳纤维复合材料结构具有密度低、模量高、强度高、疲劳性能好等优点，近年来大量应用于民用飞机机身壁板设计。机身壁板重量占比超过机身总重量的40%，在压缩载荷下，壁板会出现蒙皮屈曲、长桁压损、壁板柱失稳等多种失效模式。为了提高壁板结构的承载效率，需要研究壁板在压缩载荷下的失效载荷、失效模式。

在欧洲Cocomat项目中，R.Degenhardt等采用有限元和试验方法研究了复合材料加筋壁板的失效特性；C.Bisagni等采用非线性有限元分析和试验方法研究了含分层的复合材料壁板在压缩载荷作用下的后屈曲特性；张国凡等采用非线性有限元模型和试验研究了端头斜削的复合材料帽型加筋壁板的后屈曲承载能力，以及包覆层对承载能力的影响；孔斌等采用ABAQUS软件研究了复合材料工型长桁加筋板在压缩载荷下的后屈曲传载机制；王彬文等提出了一种考虑参数不确定性的复合材料壁板后屈曲验证方法，并通过壁板的力学试验数据验证了模型的准确性；李真等采用分析和大型带曲率壁板试验的方法研究了机身壁板在充压载荷和机械载荷作用下的疲劳、损伤容限性能；高伟等采用工程方法研究了复合材料加筋壁板的蒙皮压缩稳定性分析问题，研究表明工型加筋壁板的局部失稳载荷高于T型加筋壁板，考虑长桁有效刚度折减系数的分析值与试验值接近；吕毅等研究了T 800碳纤维复合材料工型加筋壁板在压缩载荷下的失稳和失效破坏机理，针对薄蒙皮和厚蒙皮壁板失稳分析采用了不同蒙皮宽度的稳定性工程分析方法；闫亚斌等采用有限元和试验方法研究了铝合金整体加筋壁板的压缩承载能力，给出了蒙皮和筋条分离面设计的最优位置。

上述研究工作中，工程方法主要用于复合材料壁板的压缩失稳分析，未分析复合材料壁板的压缩失效问题。壁板的压缩失效主要基于非线性有限元方法，计算时需要进行大量的迭代，花费时间长。为了提高计算效率，需要开展工程分析方法研究，以便于大范围应用于飞机设计和迭代优化。本文采用工程方法和有限元方法研究压缩载荷下壁板的屈曲特性和失效特性，通过先进的机身壁板多轴载荷试验系统验证和修正工程分析方法，同时使用该试验系统研究充压载荷对壁板屈曲载荷的影响。

1 壁板在压缩载荷下的分析方法

机身壁板为薄壁加筋结构，在压缩载荷作用时，首先蒙皮发生屈曲，新增的载荷由未发生失稳的长桁及周围蒙皮共同承担，直到壁板发生整体失稳导致失效。考虑壁板的结构形式和尺寸，失效模式包括材料强度失效、蒙皮及长桁稳定性失效等。

1.1 材料失效

材料失效的破坏机理较为复杂，常见的失效准则包括最大应变准则、蔡—希尔准则等。

1.2 蒙皮屈曲分析

对于长宽比大于4的对称均衡铺层长平板，四边简支边界条件的轴压屈曲载荷为

式中：

N

为单位长度的载荷；

D

、

D

、

D

、

D

为蒙皮铺层的弯曲刚度；

b

为蒙皮的宽度。

四边固支边界条件的轴压屈曲载荷为

帽型长桁将蒙皮分切为帽型长桁下蒙皮、长桁之间蒙皮。长桁间蒙皮宽度大，容易出现失稳。稳定性分析时，带曲率的蒙皮简化为平板计算蒙皮失稳。蒙皮的长度选取框间距，蒙皮的宽度选取帽型长桁

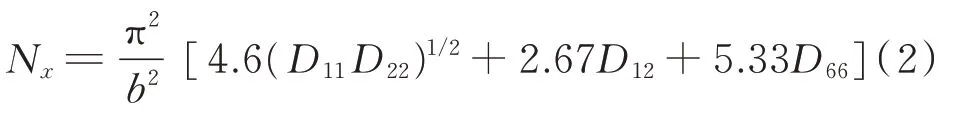
R

区之间的距离，如图1所示，蒙皮的宽度取

b

值。

图1 屈曲计算时蒙皮宽度选取Fig.1 Skin width in buckling calculation

帽型长桁和蒙皮组成一个扭转刚度大的封闭剖面，其对蒙皮支持条件强于简支，需要通过壁板级试验结果修正分析结果。

1.3 长桁压损

长桁压损是指长桁的组成单元受压时发生压溃破坏，代表长桁剖面的压缩强度性能。采用板元法计算长桁压损许用应力，帽型长桁分解为6个板元，如图2所示。

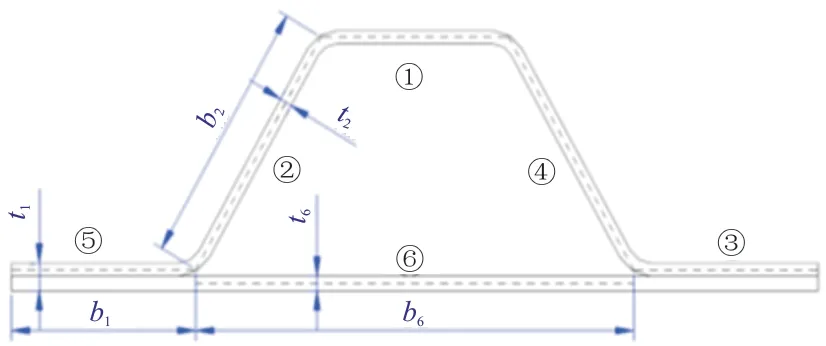
图2 帽型长桁分解示意图Fig.2 Decomposition diagram of cap-stiffened panel

计算方法如下：

最后求其加权平均值：

1.4 壁板单元在轴压下的承载能力

将复合材料壁板分解为一系列长桁与两侧蒙皮组成的柱，在压缩载荷下的失效模式为强度与失稳的混合失效模式，根据柱的长细比将柱分为短柱、中长柱、长柱。短柱的许用值为长桁的压缩强度，长柱的许用值为欧拉失稳值，中长柱采用Johnson方程计算许用应力。采用Von Karman法迭代计算蒙皮有效宽度，分析步骤如下：

（1）根据1.2节计算蒙皮屈曲应变

ε

，

ε

=

N

/

E

t

。（2）计算有效蒙皮宽度

W

，示意图如图3所示。

图3 有效蒙皮宽度示意Fig.3 Diagram of effective skin width

式中：

b

=

b

-

D

；

b

为长桁间距；

D

为帽型长桁下蒙皮间距；

ε

为工作应变。（3）计算剖面回转半径

ρ

：

式中：

A

为剖面面积；

E

为剖面轴向刚度；

I

为剖面最小弯曲惯性。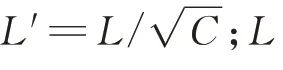

（5）根据1.3节，计算整个剖面的压损应力

σ

，计算中长柱临界应力：

（6）计算临界压缩屈曲应变：

（7）比较

ε

和

ε

，如果不相等，采用

ε

代替

ε

，重复步骤（2）~步骤（6）；如果

ε

和

ε

相等，则

ε

为中长柱临界压缩失稳应变，对应的

σ

为长柱临界压缩失稳应力。

1.5 有限元分析

采用有限元建模软件建立壁板的细化有限元模型，根据试验设备加载和约束边界，试验件一端固定，另外一端建立刚性连接单元RBE2（Rigid Body Element，Form 2）来施加载荷，保证有限元分析时端部变形与试验实际加载一致。采用大型有限元分析软件MSC.Nastran的SOL 101求解器进行静力分析，得到压缩载荷下壁板试验件的位移分布、应变分布。采用SOL 105求解器进行模态分析，得到壁板在压缩载荷下的屈曲载荷以及对应的屈曲模式。

2 试验装置及试验介绍

2.1 试验加载装置

壁板试验采用机身壁板多轴载荷试验装置，试验时加载压缩载荷及充压载荷。试验装置如图4所示，试验装置尺寸约为4 m×6 m×5 m，试验装置的载荷加载均匀性已经得到验证。

图4 试验装置照片Fig.4 Photo of test system

通过2个轴向液压作动筒同步施加压缩载荷，如图5（a）所示。为避免出现偏心加载，试验件设计时尽量将试验件压心与加载作动筒轴线保持一致。试验件与试验夹具组成封闭空间，通过充气口充气实现充压载荷的加载，如图5（b）所示。

图5 试验压缩和充压载荷加载系统Fig.5 Test loading system of compression and pressure load

2.2 试验件设计

根据壁板的结构形式和试验设备，确定试验件为5框8长桁的带曲率壁板结构。试验件中间2个框距3个长桁距的壁板是考核区，周围1个框距2个长桁距的壁板是边界过渡区。与单框距试验件比较，大尺寸的试验件可以提供更真实的支持条件，能够同时施加压缩和充压载荷。试验件长度为3 100 mm，曲线宽度为2 150 mm，曲率半径为2 960 mm，框距为620 mm，长桁距为210 mm，试验件示意图如图6所示。长桁为封闭帽型剖面，壁板为蒙皮和长桁整体成型的结构，框为Z型剖面，框、剪切角片、蒙皮之间通过高锁螺栓连接。试验件四周布置碳纤维加强片以提高连接区强度。

图6 试验件数模示意图Fig.6 Schematic diagram of digifax for test-piece

试验件采用中模高强碳纤维自动铺丝/铺带预浸料制造，预浸料单层厚度

t

=0.187 mm，材料的基本强度性能如下：

E

=154 GPa，

E

=8.5 GPa，

G

=4.2 GPa，

μ

=0.35。蒙皮铺层为［45/-45/-45/90/45/0］；长桁铺层为［45/0/0/-45/90/-45/0/0/45］；框和剪切角片铺层为［45/-45/0/90/45/-45/0］。

2.3 试验过程及结果

在试验件上布置应变片测量试验件考核区的应变大小和方向。试验件考核区蒙皮及长桁应变片布置如图7所示。蒙皮上下表面分别布置应变花，测量0°、90°方向应变和剪应变。长桁内外表面布置单片，测量长桁轴向应变。通过载荷—应变曲线的变化确定蒙皮的屈曲载荷。

图7 考核区应变片贴片图Fig.7 Strain gauge layout in focus area

首先进行试验预试，对试验件安装及试验装置进行调试，通过预试数据确认试验件在压缩载荷下应变分布均匀性，考核剖面的预试应变数据如图8所示，同一剖面的应变分布均匀。

图8 典型剖面长桁应变分布Fig.8 Strain distribution of typical section stringer

根据预估屈曲载荷逐级加载压缩载荷，加载过程中对蒙皮、长桁应变进行实时监控，应变曲线显示蒙皮出现明显屈曲后逐级卸载。载荷卸载后首先进行目视检测，然后采用A扫设备进行超声检测，均未出现新增损伤。

施加充压载荷至1倍Δ

P

并保持气压，开始逐级施加压缩载荷，研究充压载荷对蒙皮屈曲的影响。

最后进行破坏载荷试验，对试验件进行逐级加载，直至试验件破坏，破坏模式为中长柱失稳引起的壁板横向断裂，试验件破坏示意图如图9所示。

图9 试验件破坏位置示意图及照片Fig.9 Failure diagram and photo of test article

试验件典型应变曲线如图10所示，可以看出：蒙皮上下表面应变片出现拐点，蒙皮发生屈曲，之后新增载荷由长桁承载，长桁上下的应变片稍微晚些出现拐点，最后长桁应变片斜率出现急剧变化，壁板迅速破坏，发生横向断裂。根据试验结果，蒙皮屈曲对应的载荷为1 359 k N，对应的线力为201.1 N/mm，应变为1 964με；破坏载荷为2 166 k N，对应的线力为320.6 N/mm，对应的线性应变为3 130με。

图10 典型应变片的蒙皮、长桁应变曲线Fig.10 Strain curves of typical skin and stringer location

3 强度分析与试验结果对比

3.1 试验件屈曲载荷分析

（1）屈曲载荷工程分析

分析时曲板简化为平板，蒙皮长度为620.0 mm，长桁

R

角之间蒙皮宽度为145.9 mm。蒙皮屈曲载荷在简支、固支边界条件下的计算结果如表1所示，可以看出：简支边界条件的分析比试验结果偏小35.2%，固支边界条件的分析比试验值大6.2%。

表1 工程分析、有限元分析与壁板试验结果对比Table 1 Comparison of engineering analysis，finite element analysis and panel test results

由于帽型长桁为封闭剖面，扭转刚度比较强，长桁对蒙皮的支持强于简支。工程分析时，将图1中相邻长桁

R

角之间宽度为

b

的壁板结构等效为平板蒙皮，没有考虑帽型长桁底边对蒙皮弯曲刚度的贡献，工程计算时蒙皮的弯曲刚度略小于实际结构的弯曲刚度。

通过细化有限元方法研究曲率对板压缩失稳载荷的影响，分别建立平板和带曲率板的模型，铺层为蒙皮铺层，板的尺寸为620 mm×145 mm，带曲率板的曲率半径为2 960 mm，边界条件设为简支。通过MSC.Nastran软件进行线性屈曲分析，平板的1阶屈曲模式为5×1模态，带曲率板的屈曲模态为4×1模态，如图11所示。带曲率板的压缩屈曲载荷为133.8 N/mm，平板的压缩屈曲载荷为131.1 N/mm，带曲率板的屈曲载荷比平板屈曲载荷大2.0%，由于板曲率半径较大，曲率对屈曲载荷影响较小。

图11 平板与带曲率板压缩载荷模态对比Fig.11 Comparison of compression load modes between plate and plate with curvature

综上所述，采用简支、固支平均的结果比试验值偏保守14.5%，分析比试验结果略保守，可以用于工程的快速评估。

（2）屈曲载荷有限元分析

采用MSC.Patran对试验件进行建模，单元采用shell元，单元尺寸约10 mm，根据材料性能和铺层确定单元属性。分析模型的边界条件根据试验夹具与试验件连接形式确定，有限元模型示意图如图12所示，约束和加载根据试验设备加载情况施加。

图12 有限元模型示意图Fig.12 Finite element model

采用MSC.Nastran进行线性屈曲分析，屈曲模态如图13所示，屈曲载荷如表1所示，分析值比试验值大21.4%，分析结果不保守。分析值比试验值偏大的原因包括结构受载时的非线性响应和试验件的制造偏差，常见的制造偏差包括蒙皮表面的不平整、层板厚度偏差、纤维的局部弯曲等，上述偏差在较小的范围内是可以接受的。由于上述原因，结合工程经验，有限元线性屈曲的分析结果需要考虑0.8的折减系数。

图13 试验件屈曲模态图Fig.13 Buckling mode of test article

3.2 充压对稳定性的影响

在飞行过程中，机身客舱有1倍Δ

P

的充压载荷，壁板同时承受压缩载荷和充压载荷，充压载荷对蒙皮屈曲有较大的影响。

试验时首先施加充压载荷至100%，然后气压保持，开始逐级施加压缩载荷，加载至纯压缩屈曲载荷的1.3倍，蒙皮未出现屈曲。通过有限元法进一步研究，施加充压和压缩载荷时，压缩载荷为压缩工况屈曲载荷的1.48倍，充压能大幅提高蒙皮的屈曲载荷。

3.3 壁板承载能力分析

根据层板许用值试验结果，选取开孔压缩许用值-5 528με作为压缩许用值输入。根据1.3节方法，得到长桁的压损许用应力为259.7 MPa。

按照1.4节所述，采用迭代法计算壁板承载能力，壁板的长细比

L′

/

ρ

=39.2，以

ε

=3 000με作为迭代初始应变，计算有效宽度

W

、横截面积

A、

剖面惯性矩

I

等值，主要迭代过程计算如表2所示，最后计算得到的失效应力为227.9 MPa，对应的失效应变为

ε

=2 770με。试验件破坏对应的应变为

ε

=3 130με，

ε

/

ε

-1=-11.5%，分析值比试验值小11.5%。

表2 壁板承载能力计算迭代过程Table 2 Calculation iterative process of panel loading capacity

4 结 论

（1）采用简支、固支平均的分析结果比试验结果略保守，可以用于工程的快速评估；有限元线性屈曲分析得到的蒙皮屈曲值大于试验值，需要考虑修正系数。

（2）充压能大幅提高蒙皮的压缩屈曲载荷，施加充压和压缩载荷时，压缩载荷为压缩工况屈曲载荷的1.48倍。

（3）采用有效宽度法修正的中长柱失稳方法计算壁板压缩承载能力，分析结果比试验略保守。