一种适用于进近尾流间隔缩减的机型聚类方法

张竞予，桑保华，田勇

（南京航空航天大学民航学院，南京211100）

0 引 言

机场的通行效率在很大程度上依赖于空管的运行控制能力和航空器之间的安全间隔，而我国各大机场仍然采用较为保守的尾流间隔标准，没有最大化地释放跑道容量。例如，国内近距平行跑道机场尚未推广使用配对进近或配对离场，而是以隔离运行模式为主，一条跑道仅用于连续进近，另一条跑道用于起飞离场，其安全间隔参照单跑道的间隔标准实施航空器管制，保留了较大的安全裕度。在保证安全的前提下改进现行的尾流安全间隔，有利于解决民航运输的供需矛盾，因此，国内外对尾流间隔的合理性展开了深入研究，主要成果有：NASA提出航空器尾流间隔系统（Aircraft Vortex Spacing System，简称AVOSS），可以预测出动态变化的尾流间隔，实际使用情况表明，该系统能够将拉斯沃思机场跑道容量提升6%左右；L.M.B.C.Campos等于2016年提出了关于前机的尾流湍流对后机滚转稳定性影响理论，从而得出安全间隔距离的公式，可用于直接计算纵向间隔，是一种较为精准的研究手段，但是对所需气象数据要求较高；魏志强等用统计分析的方法建立了基于风速的动态尾流间隔计算模型，该模型对安全间隔的缩减效果和风速成正比，可以将跑道容量提升5%左右；潘卫军等基于尾流间隔数值计算模型对B738跟随A 359的尾流间隔进行了仿真计算，结果表明，现行间隔标准仍有很大的改进空间；何昕等构建了CSPRs起飞尾流间隔模型，并以B737跟随B747为例进行验证，仿真结果显示优化后的尾流间隔满足安全运行需求。可以看出，在上述研究中，航空器尾流演化模型有待进一步完善，且尾流间隔缩减系统多为研究一组或几组配对机型的尾流安全间隔，而不是研究尾流间隔标准的缩减效果。如果研究成果是一个巨大的尾流安全间隔矩阵，会严重增加管制员的工作负荷。针对上述问题，可以采用机型聚类的方法对航空器分类，根据新的航空器分类结果构建缩减后的尾流间隔标准，分析其缩减效果。

在航空器机型聚类的研究中，王小明等使用模糊聚类方法对不同机型进行归类，但聚类的数据中缺少翼展、机翼面积等航空器性能参数，研究成果主要应用于运营管理及保障工作；张朋等使用模糊聚类算法对航空器燃油消耗的相关数据进行了聚类分析，实验结果表明，聚类的有效性指数较好，能够有效地提取出燃油消耗指标相似的机型，但不能直接用于航空器的尾流等级分类。

因此，本文通过研究隔离运行模式下连续进近着陆的航空器尾流安全间隔缩减方法，针对不同的配对机型计算出新的尾流安全间隔；对航空器性能数据展开聚类分析，根据机型聚类结果构建新的尾流安全间隔标准，同现行尾流安全间隔标准进行分析比较，用于验证尾流间隔缩减方法的实用性。

1 进近航空器尾流安全间隔缩减设计

当前后连续进近着陆的航空器沿同一航线飞行时，其航迹基本保持一致，如果受到较大侧风影响，后机有可能受到前机尾流的影响，如图1所示。

图1 进近航空器尾流遭遇示意图Fig.1 Schematic diagram of approach aircraft wake encounter

式中：

V

为侧风大小；

Γ

为涡流环量。另外，本文基于尾流的两阶段衰减模型，将进近尾流的消散过程分为初始消散阶段和快速消散阶段分别展开描述。在进近尾流的初始消散阶段，设定尾涡初始消散时间为

t

，从尾流开始生成到

t

时刻这段时间内，尾流的强度变化会受到大气湍流的影响，并与初始涡间距

b

、参考时间

t

等参数有关。根据文献［10］中的相关数据，得到进近尾流初始消散强度变化规律满足如下关系式：

式中：

W

为升力；

ρ

为空气密度；

V

为空速；

s

为机翼载荷因数；

b

为翼展；

Γ

为初始环量。尾涡初始消散时间

t

与参考时间

t

之间的关系，可以用Sarpkaya提出的无因次尾涡开始消散的时间

t

与无因次紊流度

ε

之间的关系来计算，具体过程在此不作赘述。

由于航空器在进近着陆阶段的飞行高度较低，尾流的消散过程会受地效影响，当进近尾流进入快速消散阶段后，尾涡强度变化规律可描述为

式中：

t

为尾涡进入快速消散阶段的时间；

y

与

z

分别为尾涡的侧向坐标位置与高度坐标位置；

N

为浮力频率，又叫B-V频率，用于表征大气稳定度。

由于跑道参数确定后，航空器运行程序一般不发生较大变化，本文从尾流间隔动态化的角度探讨最后进近阶段的尾流间隔缩减问题，即采用基于滚转力矩系数的尾流分析模型直接计算尾流的临界消散时间，具体如下：

首先，考虑连续进近着陆过程中后机进入前机尾涡中心的情形，通过计算滚转力矩和滚转力矩系数（Rolling Moment Coefficient，简称RMC），判断后机遭遇尾流时的严重程度，同时获取相应临界尾流强度以及该时刻下最优的尾流间隔，公式为

参考文献［12］，假设后机机翼满足椭圆翼弦分布，前机产生的尾涡满足B-H环量分布且作用在后机机翼上，则

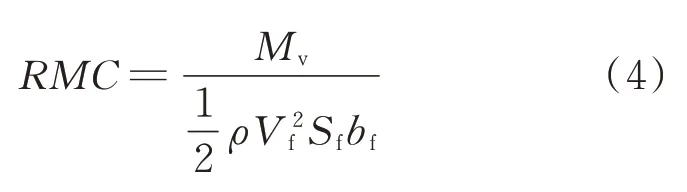
RMC

可被表达为包含翼展跨度比

b

/

b

的函数，如下：

式中：

AR

为机翼纵横比；

V

为后机速度；

ε

为关于跨度比

b

/

b

的函数；

b

和

b

分别为前机翼展和后机翼展。其次，考虑航空器运行到最后进近阶段后的情形，此时航空器产生尾流的高度通常在60 m以下，尾流运动会受到地面效应的影响，进近前后航空器之间所需保持的最小时间间隔

t

和纵向间隔

L

为

上述尾流间隔缩减方法计算了在进近着陆过程中前后两架航空器的临界尾流安全间隔，即计算了指定机型下的尾流安全间隔，尚未考虑不同机型类别下的尾流间隔标准。因此，本文将航空器机型聚类方法和临界尾流安全间隔相结合，构建缩减后的进近航空器尾流间隔标准。

2 基于层次聚类的航空器机型分类

2.1 层次聚类算法的计算流程

航空器机型聚类是通过聚类算法对航空器进行分类的过程，聚类算法以

K

均值、层次聚类算法为代表。其中，层次聚类算法不仅可以划分多个层次的数据，还能够通过树状结构图表现出不同数据的相关性，因此，研究采用自底而上的层次聚类算法（Aggregative）对民用航空器进行分类，获取部分空客航空器的机型聚类结果如图2所示。

图2 部分机型的层次聚类结果Fig.2 Hierarchical clustering results of some aircraft types

层次聚类算法的计算流程如下：

（1）初始化：将每个对象看成一个簇

C

=［

x

］，

i

=1，2，…，

N

；（2）迭代：设定终止条件为聚类簇的数量

K

，计算聚类簇之间的距离，找出距离最近的两个簇，将这些簇根据某种规则一步步合并，不断合并直到达到预设的簇类个数。聚类簇合并的依据是点间距离最小，计算点间距离的方法主要有三种，分别为Single Linkage、Complete Linkage和Average Linkage。其中，Average Linkage的计算方法是计算两个点集中每个数据点与其他所有数据点之间的距离，以所有距离的平均值作为两点集之间的距离。虽然计算量较大，但它能更好地避免极值的影响，故本文选用这种方法来计算点间的距离。

2.2 航空器性能参数的聚类指标选取

聚类指标是聚类分析的基本输入条件，它们代表着不同类别的属性特征。在航空器分类标准中，国内尾流间隔标准简单地以航空器重量为分类依据，将航空器划分为3类；欧美RECAT以航空器重量和翼展为分类依据，将航空器划分为6类；RECAT-CN（广州白云国际机场、深圳宝安国际机场试行）是在国内现行尾流间隔的基础上，效仿欧美RECAT的航空器分类技术，根据翼展和重量两个性能参数，仅仅将重型机做了具体的分类（B类和C类）。

因此，本文参照进近尾流安全间隔模型，从前机产生的尾流强度和后机可接受的临界滚转力矩系数两方面出发，在BADA航空器性能数据库中选取机型聚类指标，展开更为精细的航空器聚类分析。所选取的与前机尾流强度有关的指标有：

C

—翼展（m）、

C

—进近阶段平均质量（t）、

C

—起飞速度（m/s）、

C

—进近速度（m/s）。所选取的与后机能接受临界强度有关的指标有：

C

—起飞阶段发动机推力（N）、

C

—进近阶段发动机推力（N）、

C

—机翼诱导阻力系数和

C

—寄生阻力系数。

部分机型指标参数如表1所示。

表1 部分机型指标参数Table 1 Specifications of some models

2.3 基于主成分分析法的聚类指标降维

随着数据集维度的增加，算法学习需要的样本数量呈指数级增加，在高维数据提取与处理的过程中，一般会采取降维的手段对高维特征向量进行处理，如线性判别式分析法和主成分分析法等。鉴于航空器性能数据维度较高，且某些数据具有一定的相关性，本文选取主成分分析法PCA（Principal Component Analysis，简称PCA）对机型指标参数进行降维。PCA常用于提取数据的主要特征分量，该方法是一种无监督学习方法，且计算简单，适用于区分同一样本类，其求解步骤为：（1）设定原始数据为

m

条

n

维数据，所需求的维度为

k

，将原始数据按列组成

n

行

m

列矩阵

X

；（2）将

X

的每一行（代表一个属性字段）进行零均值化；（3）求出协方差矩阵；（4）求出协方差矩阵的特征值及对应的特征向量；（5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前

k

行组成矩阵

P

，该矩阵即为降维到

k

维后的数据。使用PCA降到3维（

P

、

P

、

P

）的部分数据结果如表2所示，其中（

P

、

P

、

P

）代表一组数据中被提取的主成分信息，无实际意义。

表2 基于PCA方法的降维数据Table 2 Dimensionality reduction data based on PCA method

3 机型聚类下的航空器进近尾流安全间隔效果

3.1 航空器进近尾流安全间隔仿真验证

3.1.1 仿真参数设置

通过MATLAB软件的SIMULINK模块，搭建进近航空器尾流间隔缩减系统，并以长沙黄花国际机场东跑道的进场航班数据为仿真对象。考虑到2020年5月的航班逐渐恢复正常且较稳定，单日进场航班数量在160架次左右，且航空器类型的占比与正常时段差异较小，本文选取2020年5月14日的航班计划数据以及长沙黄花国际机场的气象数据进行仿真。数据表明，该机场的常用机型以中型机为主，占比在97%以上，轻型机和重型机分别占比1.2%左右。另外，统计当日的气象数据，根据不同速度的侧风在24小时内所占的比例及该日环境温度的变化情况，仿真过程中设置

ε

为0.01，

N

为0.3，侧风的大小为-1~3 m/s之间，

RMC

值参考欧控测得的临界滚转力矩系数数据。

3.1.2 仿真结果及分析

由航班计划数据可知，该日航班中型机A 320与B738所占比例最大，重型机以B744、A 333和A 330为主。本文选取以下三种机型配对仿真，第一组：B738跟随A 330；第二组：A 320跟随B744；第三组：A 320跟随B738。三组机型配对条件下最后进近阶段的仿真结果如表3所示。

表3 三组机型配对条件下最后进近阶段的仿真结果Table 3 Simulation results of the final approach stage under condition of three groups of aircraft pairing

从表3可以看出：根据第一组仿真结果，当B738中型机跟随A 330重型机时，临界耗散时间为85.29 s，纵向间隔为6.3 km，侧风对尾流侧向飘移影响较大；根据第二组仿真结果，当A 320中型机跟随B744重型机时，耗散时间在75 s以内，尾流临界消散的时间明显加快；根据第三组仿真结果，中型机之间尾流间隔也有较好的缩减效果。

3.2 机型聚类效果

通过改变聚类的簇数，分别将航空器聚成三、五、六类，并与现行尾流间隔标准（轻型机、中型机、重型机）、广州和深圳机场试行的RECAT-CN（J、B、C、M、L）、欧美RECAT标准（A、B、C、D、E、F）对应，用于设定相应航空器分类等级（如表4所示），从而获取本文所提出的航空器尾流间隔缩减系统的使用效果。

表4 基于PCA方法降维的航空器聚类Table 4 Aircraft clustering based on PCA method dimensionality reduction

3.3 进近尾流间隔效果对比分析

根据航空器类型聚类结果可以看出，仿真过程中第一组和第二组配对航空器的机型分类一致。因此本文分别以第一组和第三组配对机型的情况为例，设定相应的尾流间隔标准，获取相应的安全间隔缩减效果，如表5~表6所示。

表5 第一组机型尾流间隔缩减效果对比Table 5 Comparison of the reduction effect of the wake interval of the first group of models

表6 第三组机型尾流间隔缩减效果对比Table 6 Comparison of the reduction effect of the wake interval of the third group of models

从表5~表6可以看出：采用本文的尾流缩减方法后，主流配对机型的临界尾流安全间隔均可以控制在7 km以内，与现行的尾流安全间隔标准及广州试行的RECAT-CN相比，可以缩减0.4 km以上；与欧美RECAT尾流间隔具有较好的一致性。

4 结 论

本文所提出的航空器分类方法与国内外所使用的分类方法具有较好的一致性，且计算出的进近航空器临界尾流间隔可以比国内现行尾流间隔标准缩减0.8 km以上，而且相比于欧美RECAT尾流间隔标准也具有一定的缩减效果。