三平移并联机器人的结构优化设计与运动学多目标分析

郑 丰，陈 彬，李世恒，曹 鹏

（中国南方电网有限责任公司超高压输电公司天生桥局，兴义 562400）

0 引言

三平移并联机器人因其内部的自由度并联结构，而推广运用到机械处理过程中。随着并联机械结构不断地发展，研究人员将多个相互独立的传动部件并行连接，控制机架在直线运动部件之间形成闭环系统，组装形成结构稳定的机器结构[1]。并联机器人在动力的支持下，能够在行驶的平面内产生不同大小的转角，来支持并联机器人的正常工作，但针对机器人结构进行运动学分析时，机器人内的并联结构存在弹性变形，并联机器人在正常工作的过程中，极易产生柔性耦合。也就导致构建运动学多目标分析方法时，目标精度较小。不符合机器人的使用运行要求，为合理解决柔性耦合产生的不适配，优化并联机器人结构成为了当下的研究热点。

国外研究并联机器人起步较早，自二十世纪三十年代起，研究人员研制出了球面并联机构，研制出了六自由度的并联机构，增强了机器人的运动灵敏性[2]，引用了位置正解计算方法构建了运动学多目标分析方法。国内研究并联机器人起步较晚，研究人员运用空间复杂坐标构建了机器人变化模型，并根据机器人并联结构设计了结构分解技术，优化处理了多种机器人结构，在分析运动学多目标时，应用了空间矢量变换方法模拟并联机器人运行过程，分析机器人运动学多目标分析方法。文献[3]内构建的运动学多目标分析方法，以并联机器人工作空间和全局灵巧度作为优化指标，采用差分进化算法建立了运动学目标数值关系。文献[4]中的运动学多目标分析方法，优化处理机器人的结构为运动解耦的非对称三平移输出的并联结构，并运用了方位特征方程构建了运动学多目标分析方法。经阶段性的应用验证可知，现有的运动学多目标分析方法指标精度较小，由此可知，优化设计三平移并联机器人结构，并构建运动学多目标分析方法具有发展性意义。

1 三平移并联机器人的结构优化设计与运动学多目标分析

1.1 重构三平移并联机器人传动支路

三平移并联机器人内的并联结构内部集成了抗干扰的滤波器，所以在重构三平移并联机器人传动支路时，调整并联机器人运动轴的运行状态，并在运动轴内配置直线光栅尺，在运动轴与机器人传感器之间形成一个尺度反馈。在传感器与机器人运动轴之间放置第二编码器，控制滤波器对传感器产生的振荡，影响传感器数据传输过程。使用传感器反馈得到的三平移并联机器人的精度参数，在并联机器人中形成一个数值反馈，精度参数的数值关系可表示为：

其中，R表示计算得到的精度参数，p（s）表示传感器反馈得到的周期精度函数，R（s）表示并联机器人的处理半径。当并联机器人实现三平移后，将该精度数值补偿处理到并联机器人的命令控制当中。根据上述计算得到的精度参数可知，调整传感器的安装位置后，并联机器人结构应满足并联支架的支撑，运用Von Mises屈服准则，计算支持并联支架的应力数值，计算公式可表示为：

其中，σ表示计算得到的应力数值，M表示结构倒角。在该应力数值控制下，调整传感器位置点形成全闭环结构，如图1所示。

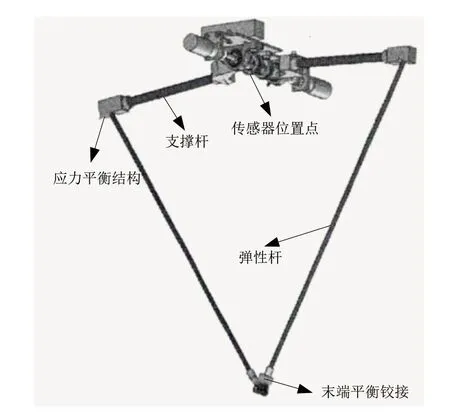
图1 形成的全闭环结构

在图1所示的全闭环结构内，调整传感器安置位置点在支撑杆结构的并联中心，此时，并联机器人就形成了以传感器位置点作为并联中心的结构。重构三平移并联机器人传动支路，建立机器人刚度数值模型。

1.2 建立机器人结构动力学方程

以上述优化后的全闭环位置作为处理基础，在建立结构动力学方程时，采用整体刚度方法建立刚度矩阵，数值关系可表示为：

其中，P表示刚度矩阵，ki表示上端机器人分块刚度，di表示机器人支撑结构的分块矩阵。由上述构建的刚度矩阵可知，上端机器人结构单元刚度参数与整体刚度呈对角原则，将结构处理为整体化的力学平衡方程，设定机器人驱动力形成的位姿状态，定义该状态产生的力学平衡，数值关系可表示为：

其中，PF表示力学平衡数值，Pi表示上端机器人结构的外部作用力，D表示上端机器人结构产生的位姿态变化。支撑杆尺寸的不同，机器人形成了外力不平衡力，为控制该不平衡力为数值0，利用切线刚度矩阵迭代处理力学平衡数值，形成切线刚度矩阵，数值关系可表示为：

其中，φ表示端点内力矩阵，d表示切线数值解，dn表示渐进参数。平衡机器人结构内存在的不平衡力数值，将上述数值处理过程作为迭代参照，应用一级泰勒展开处理逼近序列方程，确定切线刚度的应力项，联立上述数值关系3）、5），将机器人位姿矢量维持在矢量同步变化的状态，控制支撑结构发生刚度作用形成的柔性位移[5]，构建形成机器人的数值模型，在该数值关系控制下，将上述整理得到的运动指标作为运动学多目标，构建多目标分析算法。

1.3 构建运动学多目标分析算法

将上述指标处理为运动能量的形式，并构建机器人运动学方程，数值关系可表示为：

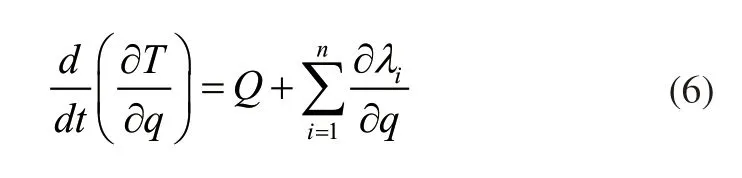
其中，T表示机器人的能量数值，q表示广义坐标矩阵，Q表示广义条件下的力矩阵，λi表示约束力的反作用力。将上述数值关系处理为一般形式，将其处理为多分量的形式，数值关系如下：

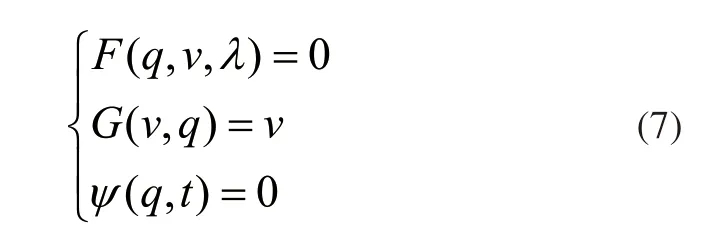
其中，v表示机器人的运动速度，F表示机器人的动力微分方程，G表示设定的非完整约束，ψ表示约束条件下的参数，其余参数含义不变。将上述处理的分量作为展开约束[6]，在确定机器人的行驶速度参数后，应用约束反力求解速度与约束反力之间的数值关系，数值关系可表示为：

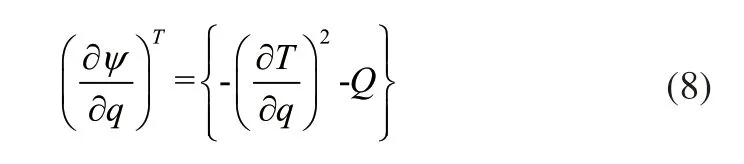
上述数值关系中，各项参数含义不变。在三平移并联机器人的结构当中，单个并联结构内的连杆之间会在内部形成一个驱动力，影响机器人产生的运动过程，定义机器人内部驱动力向外产生的运动驱动，并处理为惯量参数，数值关系可表示为：

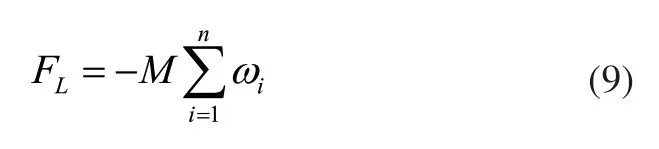
其中，FL表示处理形成的惯量数值，wi表示机器人内部连杆的角速度，n表示连杆之间形成的夹角。将上述处理的惯性参数处理为分析算法中的固定数值，调整该数值的矢量状态后，最终形成运动学多目标分析算法。

2 测试分析

2.1 实验准备

准备搭建平移机器人的零部件材料，标定机器人结构的材料属性，组成机器人零部件材料及运动学参数如表1所示。

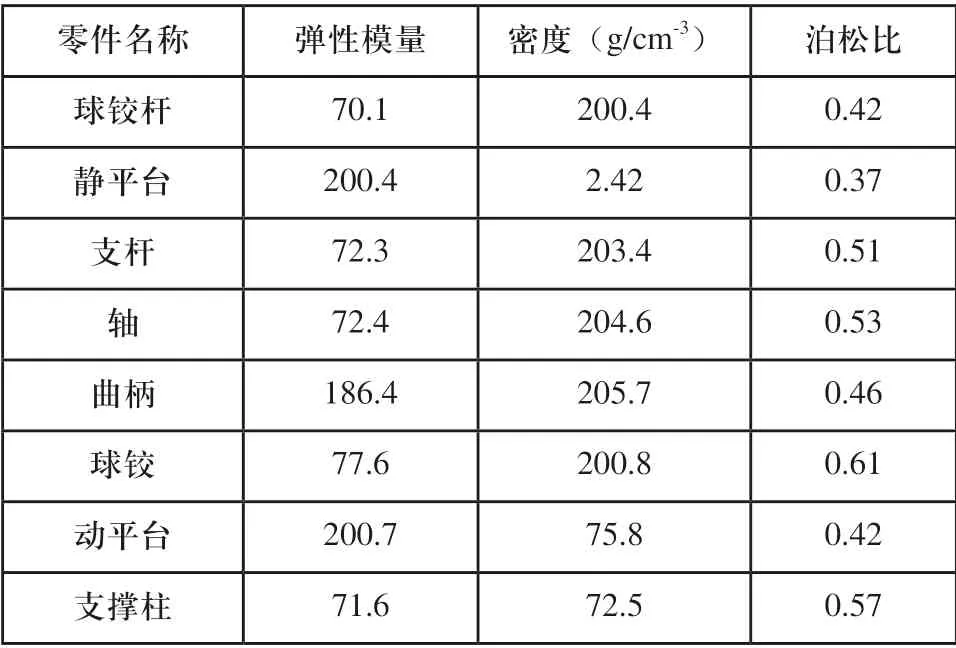
表1 并联机器人零部件名称及运动学参数

使用表1参数所示的零部件，组装并联机器人零件后，在机器人内部设置三个运动副、五个球面副以及两个转动副，调节运动副与球面副后，控制静平台固定在气浮环境内，设置气浮环境内的测量值为5kHz，控制外部环境对并联机器人的影响，组装形成的并联机器人结构如图2所示。

图2 组装形成的并联机器人结构

使用上图所示的并联机器人结构，采用曲线运动的形式规划并联机器人的行驶路线，将机器人的的行驶路线使用SOLIDWORKS模型导入至ADAMS软件当中，构建形成一个动平台下的三维机器人运行过程。实验平台搭建完毕后，应用基于时空差异的运动学多目标分析方法、基于柔性动力学的多目标分析方法与所设计的多目标分析方法进行实验，对比分析三种多目标分析方法的性能。

2.2 结果及分析

基于上述实验准备，采用自适应阻抗力控制装置放置在组装形成的机器人结构当中，在自适应控制与平台之间放置一个六维传感器，实时反馈机器人运动过程产生的位置响应，选定三种多目标分析方法中机器人优化处理过程，设定机器人程序内的并联机器人的位移数值，并以该位移数字作为标准对比参数，设置机器人的位移时间为60s，在该时间区间内，统计并整理三种多目标分析方法的位置响应结果，如图3所示。

图3 三种多目标分析方法的位置响应曲线

由图3所示的位置响应曲线可知，在模拟标定的行驶路线内，整理时间区间内产生的位移，图中的B曲线为设定的标准位移数值，可知在设定的时间范围内设定的机器人位移数值变化为1400mm，机器人移动过程平稳。在第0s～20s时，三种运动学多目标分析方法均产生了位移激增，第20s以后，代表基于时空差异的运动学多目标分析方法的A曲线，机器人产生的位移数值反复在1600mm～1800mm之间变化，并联机器人形成了一个反复滑动的过程，影响了并联机器人的使用。代表基于柔性动力学的多目标分析方法的D曲线产生了数值波动，机器人形成的位移数值在1000mm～1200mm之间，与机器人设定的位移数值相比，该种分析方法控制机器人行驶的位移数值较小，且机器人运行出现滑动不稳的现象。代表所设计多目标分析方法的C曲线在第30s时，形成的位移数值出现了波动，但最终趋向于平稳，结构优化处理的机器人位移数值变化在1400mm左右，与设定的位移数值相差不大，且优化后的机器人结构运行平稳。

在上述实验环境下，整理并联机器人运动过程中多目标分析指标，定义指标数值关系，可表示为：

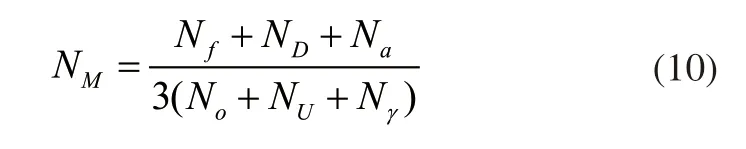
其中，NM构建的弹性模量参数，Nf表示并联机器人组成材料数值，ND表示机器人横摆参数，Na表示机器人转角参数，No表示机器人泊松比参数，NU表示机器人运行倾角，Nγ表示机器人侧向加速度。对应整理三种运动学多目标分析方法各项指标参数数值，定义运动目标指标的数值区间为0～100，当目标处理数值越大，则表示该种多目标分析方法整理的运动学指标越精确，对应整理不同指标形成的参数结果，数值结果如图4所示。

图4 三种运动学多目标分析方法指标数值结果

对应上述计算得到的目标指数，将其整理为数值网状图，根据数值结果可知，代表基于时空差异的运动学多目标分析方法的A曲线，运动学多目标处理指标数值在60左右，实际多目标处理时的指标精度较差。代表基于柔性动力学的多目标分析方法的D曲线，运动学多目标处理过程平均指标参数在20左右，实际分析处理的指标精度最差。而代表所设计分析方法的D曲线，得到的平均指标数值在80左右，与选定的两种多目标分析方法相比，所设计的多目标分析方法选定的运动学指标精度最高。

保持上述实验环境不变，设定并联机器人的行驶重力角为10°、20°、30°、40°、50°以及60°，调用三种多目标分析方法中机器人运动轨迹跟踪过程，设定机器人的运行周期为30s，对应实验给出的机器人参数，整理机器人在空间结构内的姿态，数值关系可表示为：

其中，q1、q2、q3表示设定的并联机器人行驶重力角，t表示机器人行驶时间周期。对应整理机器人产生的姿态，以机器人时间周期数值作为自变量，计算三种运动学多目标分析方法形成的外倾角，数值关系可表示为：

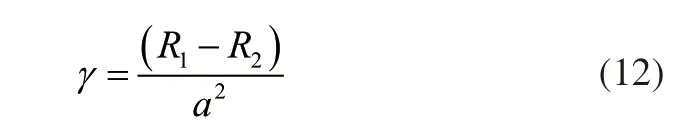
其中，R1、R2表示并联机器人的行驶半径，a表示转动参数，γ表示外倾角。对应计算得到的外倾角数值，整理三种多目标分析方法形成的姿态外倾角，数值结果如图5所示。

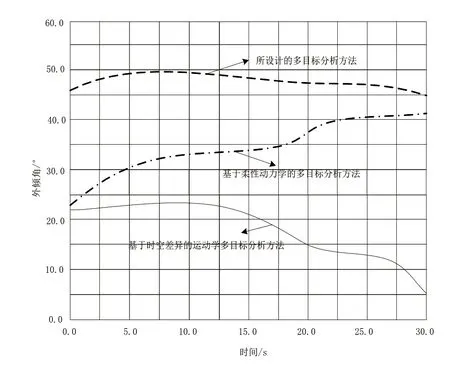
图5 三种多目标分析方法得到的外倾角结果

对应上述构建的外倾角数值关系，整理在不同处理时长条件下，多目标分析方法得到的外倾角，由上图所示的实验结果可知，当并联机器人运行处理30s后，基于时空差异的运动学多目标分析方法得到的外倾角为5°，机器人行驶过程中并联结构产生的倾角最小，三平移并联机器不能形成稳定的结构，不符合机器人的行驶实际。在相同的时间节点处，基于柔性动力学的多目标分析方法产生的外倾角数值为40°，并联机器人之间形成的夹角较大，机器人在行驶过程中平衡性较差。而所设计的多目标分析方法在相同的时间阶段处，产生的

3 结语