基于海量GIS数据的自动化故障融合监测技术

杨文佳，苗 璐，樊 玮，夏 伟

（1.广东电网有限责任公司电力调度控制中心，广州 510600；2.南方电网数字电网研究院有限公司，广州 510600）

0 引言

GIS信息由地理信息系统产生，该信息包含了地理信息以及遥感信息，能够为计算机数据处理技术提供分析对象。随着大数据技术的应用普及，海量数据处理成为了数据处理的基本处理过程，融合后的数据能够挖掘得到其内部隐含的特征信息，在自动化故障监测过程中，以该特征信息作为监测对象，能够构建形成科学地监测过程。由此可知，设计自动化故障融合监测技术具有一定的发展意义。

国外研究监测技术起步较早，研究人员最初将监测技术用于机械故障诊断与维护上，并根据机械运行参数设计了数值关系式的监测条件。国内自上个世纪八十年代展开监测技术的研究，研究人员应用了数值解析的模型整理故障融合中的数值条件，并结合数值统计学的分析方法将故障融合数据处理线性或是时序相关性，设计形成了多种监测算法。整理当下的研究成果可知，董怀普、王位杰等人设定了自动化设备运行规则，并采用深度优先搜索算法建立了故障数据之间的连接关系，并推算得到了监测数值条件。陈泗贞、梁竞雷等人采用相关性分析过程处理了故障数据，采用信息整合的方式将同等类型的故障数据处理为相同的数据事件，利用蛮力BF算法构建数值监测过程，构建形成故障融合监测技术。经阶段性的应用研究发现，现有的故障融合监测技术对融合后的故障数据不敏感，实际监测过程中会产生误监或是漏监的情况。为此，设计基于海量GIS数据的自动化故障融合监测技术。

1 基于海量GIS数据的自动化故障融合监测技术

1.1 利用GIS时空数据模型多尺度表达故障数据

利用GIS时空数据模型中的时空性，将故障数据处理为空间形式的数据，空间化后的故障数据可表示为：

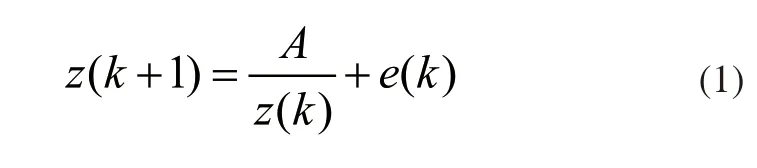
其中，z（k+1）表示空间化处理后的故障数据数值关系，A表示故障数据中的层次参数，z（k）表示故障数据的阶态向量，e（k）表示期望为0的故障数据序列。采用预处理的方式简化空间化处理的故障数据为拓扑结构，计算数值空间范围内存在的编码参数，数值关系可表示为：

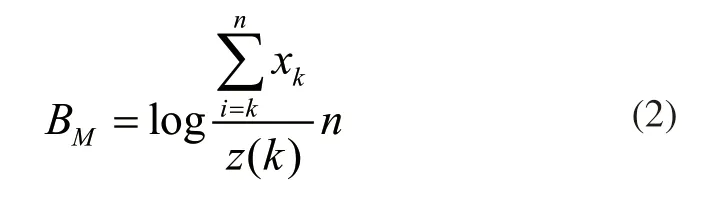
其中，BM表示计算得到的编码参数，xk表示拓扑结构中的故障数据集，n表示参与处理的故障数据数量，其余参数含义不变。为了消除编码参数计算误差所带来的尺度误差，采用DP算法调整拓扑结构中产生的数值差，调整过程可表示为：

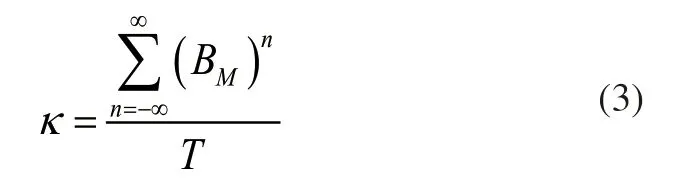
其中，κ表示设定的调整参数，其余参数含义保持原有含义不变。调整含有数值差的故障数据后，自定义拓扑结构中的故障数据，并利用故障数据建立不同尺度条件的数值约束关系，整理同尺度关系下的数据后，选定故障数据的极值数值验证对象，确定尺度条件下实际产生的包矩数值，当该数值大于0时，则表示该尺度下的故障数据符合逻辑。使用上述多尺度表达后的故障数据，设定海量数据融合规范变量。

1.2 设定海量数据融合规范变量

使用上述多尺度表达后的故障数据，根据故障数据的时间序列，在对应的时间节点处，构造故障数据的变量数值关系，数值关系可表示为：

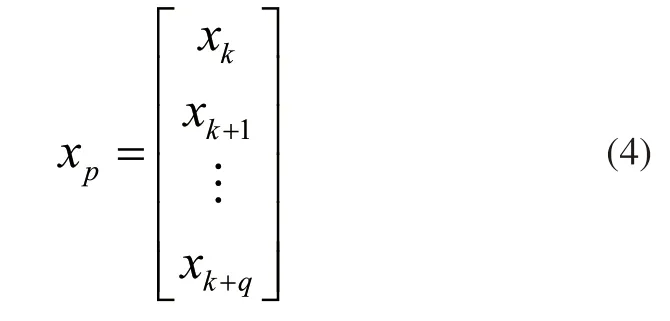
其中，xp表示不同时间序列下的故障数据变量，xk表示去均值处理后的多尺度故障数据。可知在上述变量数值关系内，数据融合时的特征值呈降序分布，故将上述计算得到的变量参数处理为协方差，参数之间的相互关系，构建变量间的转换矩阵，矩阵可表示为：

其中，J表示构建得到的转换矩阵，Vd表示特征数值中包含的参数相互关系，其余参数含义不变。选定状态空间变化指标作为度量参数，设定规范的数值关系，数值关系可表示为：

上述数值关系当中，T表示规范数值关系中的控制限参数，其余参数含义不变。当故障数据规模增大时，控制限影响下的度量参数也发生变化，将控制限参数处理为正态分布的形式，根据参与融合数据量，不断迭代处理设定的控制限数值，采用二值逼近的方式确定规范处理过程中各项参数产生的阶跃扰动，消除其他参数对规范变量产生的干扰。设定海量数据融合规范变量后，构建自动化故障融合监测方法。

1.3 设计自动化故障融合监测方法

以上述得到的规范变量作为监测过程中的约束关系，将多尺度化的故障融合数据处理为含有奇异值的形式，数值关系可表示为：

其中，σi表示含有奇异值的故障融合数据关系，λi表示故障融合数据的特征值，其余参数含义不变。将含有奇异值的故障融合数据处理为不同主元阈值的变量，并根据该变量建立监测时的子块，此时，形成的子元监测块可表示为：

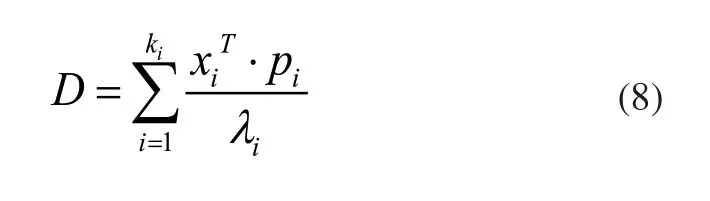
其中，D表示设定的子元监测块，ki表示融合数据的敏感主元，pi表示序号处理后的故障数据，其余参数含义不变。依次计算每个监测子块中的统计量，并将该统计量与主元阈值融合处理，构建形成特征值矩阵，并整理统计量对应的控制限参数，采用贝叶斯方法计算得到的BIC统计量，并以该统计量作为实际的监测条件，当故障融合数据超过该统计量数值时，即成功监测一次。综合上述研究设计过程，最终完成对基于海量GIS数据的自动化故障融合监测技术的设计。

2 故障融合监测测试

2.1 GIS索引标记海量自动化故障数据

调用GIS处理系统中的海量时空数据读写架构，将自动化故障数据处理为索引表与源数据表两种组成部分。调用适配器Adapter将处理得到的数据索引处理为索引元数据，调用DBZ索引结构构建一个区域聚类数据维度，将自动化数据处理为多维空间下的数据点，并采用位交错法将故障数据处理为索引编码数值，在海量数据集中设定一个数据点索引筛选结构，设定的规模筛选结构如图1所示。

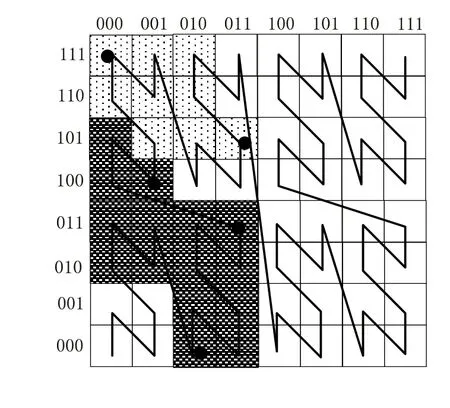
图1 设定的数据点索引筛选结构

整理筛选结构产生的自动化数据点，采用曲线编码的方式将筛选得到的数据节点数据，在节点数据范围内，定义主元敏感系数，将主元作为数值变量，整理上述筛选的数据点，构建一个GIS数值仿真过程，仿真数值结构为：

其中，xi（i=1，2，…，4）表示筛选得到的的自动化数据点，eij（i=1，2，3，j=1，2，3）表示定义的不同维度的源变量，zi（i=1，2，3）表示设定数值仿真变量。整理上述形成的数值仿真，可知在仿真过程中产生了100组数值训练样本，在筛选得到的数据样本内，设定两种类型的故障。故障1在x1维度内的数据上一个幅值为0.2的阶跃故障，故障2则是在x2属性内的数据增加0.001×（i-400）的斜坡故障。故障数据设定完毕后，为了控制设定故障数据对其他变量产生影响，引用故障重构的方式消除故障数据集中存在的观测量变化。

2.2 故障数据重构

整理上述设定故障后的数据，将其定义为原始数据集后，通过MEWMA模型滤波，将故障融合后的数据重构，重构过程可表示为：

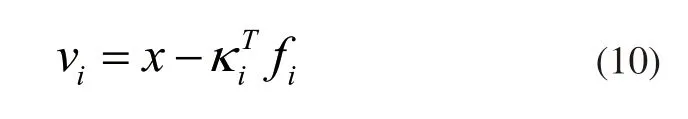
上述数值关系下，vi表示重构后的故障融合数据，κi表示模型滤波处理函数，fi表示设定的故障数据集，T表示重构周期，其余参数含义不变。使用上述重构后的故障数据，统一设定不同维度故障数据的控制限，此时设定的故障数据的控制限统计量可表示为：

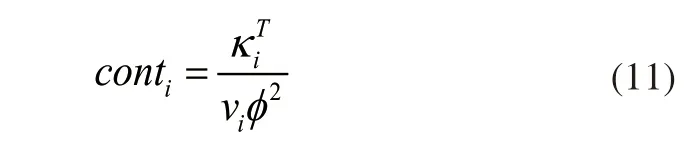
其中，conti表示设定的控制限统计量，φ表示控制限中的统计量，其余参数含义不变。针对设定的故障数据控制限统计量数值，整理故障数据在控制限数值内的统计量分布，故障数据的统计量分布如图2所示。

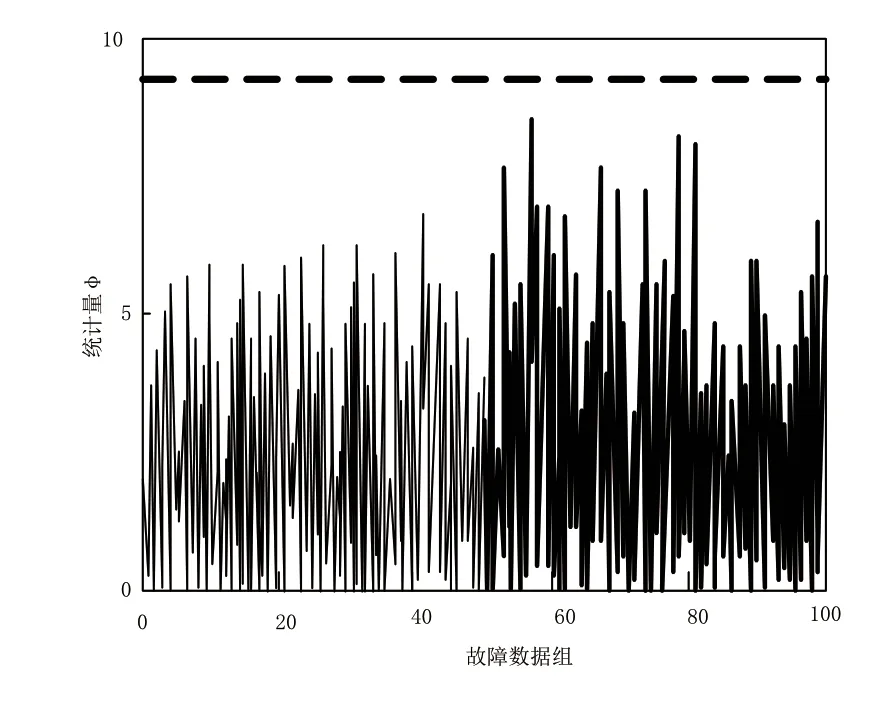
图2 故障数据的统计量分布

根据图2所示的故障数据统计量分布可知，前50组故障数据的统计量呈周期均匀变化，设定故障变量后的数据统计量出现了数值突变。以上述处理得到的统计量分布作为监测标准，应用基于深度检索的融合监测技术、基于偏最小二乘的融合监测技术以及所设计的融合监测技术进行测试。选定相同的性能指标，对比三种故障融合监测技术的性能。

2.3 监测结果及分析

基于上述数据处理，定义故障数据中的故障敏感主元，以上述设定的控制限数值作为数值限制，利用协方差矩阵分解故障数据的特征数值，分解过程可表示为：

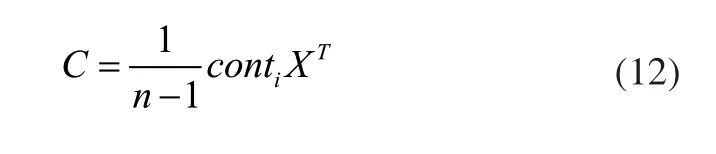
其中，C表示构建的分解矩阵，n表示参与分解的数据样本个数，X表示参与分解的故障融合数据，其余参数含义不变。以构建分解矩阵中的数值作为三种监测技术的监测点，定义三种数据融合监测技术在监测数据的监测主元系数，系数的数值关系可表示为：

其中，εi表示计算得到的主元系数，pi表示统计量的贡献率，σi表示监测奇异值。以上述计算得到的主元系数作为监测数据的触发阈值，并在平面空间范围内构建一个封闭的数值限制，根据上述设定的控制限作为监测数据的控制限，在第一主元以及第二主元的方向上，整理三种故障融合数据的监测敏感性，结果如图3所示。

图3 三种故障融合监测技术敏感性结果

定义图3中的椭圆区域范围为选定监测故障融合数据的控制限，可知三种故障融合监测技术的控制限范围相同。在两个主元方向内绘制的黑色直线则表示不同故障融合监测技术在四个主元方向上的控制限，定义当黑色直线无限趋近于数据点时，则表示该种监测技术对监测故障融合数据点敏感。由图3所示的实验结果可知，基于深度检索的融合监测技术在不同的主元条件下，四种主元所代表的黑色直线偏离数据点较远，该种监测技术对故障数据点的敏感性较弱。基于偏最小二乘的融合监测技术得到的黑色直线偏离数据点较近，该种融合监测技术对故障数据的敏感性较强。而所设计的融合监测技术得到的黑色直线无限趋近于所准备的数据点，该种故障融合监测技术对故障融合数据的敏感性最强。

根据上述整理得到的敏感度结果，整理在不同主元的方向上的主元参数，设定三种故障融合监测技术处理故障融合数据的遗忘因子为0.3，整理数值参数并处理为故障融合监测的联合指标，数值关系可表示为：

其中，Fj表示计算得到的联合指标，Hj表示对应融合监测技术内的主元参数，ω表示设定的遗忘因子，Nj表示参与监测的主元数量。以上述计算得到的联合指标数值关系作为设定自动化故障的阶跃评价指标，在固定的数据组数量内，当联合指标数值稳定变化时，则表示该种融合监测技术完成一次监测过程，已知设定的故障融合监测过程产生的联合指标参数相等，对应整理三种故障融合监测技术得到的故障采样点结果，如图4所示。

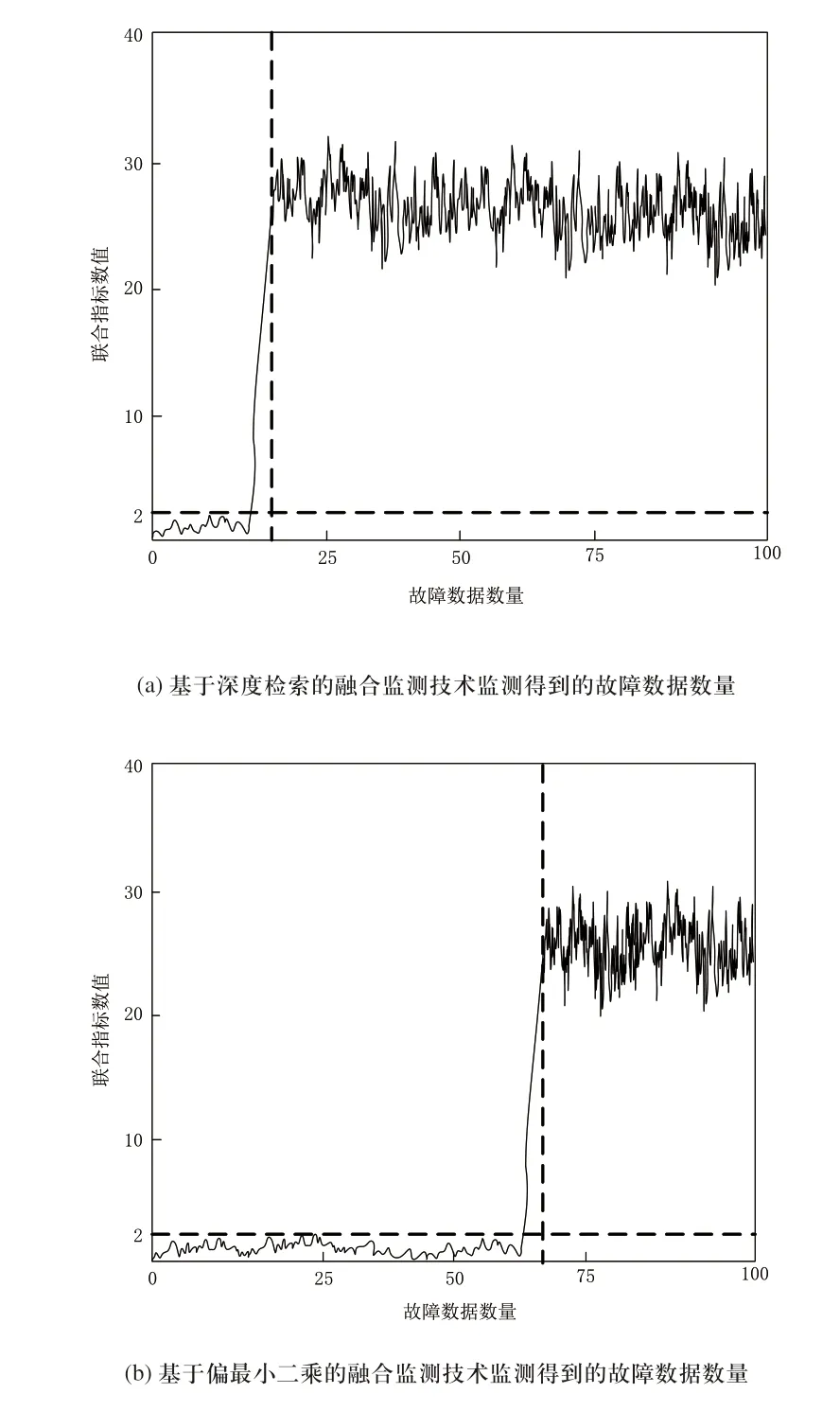
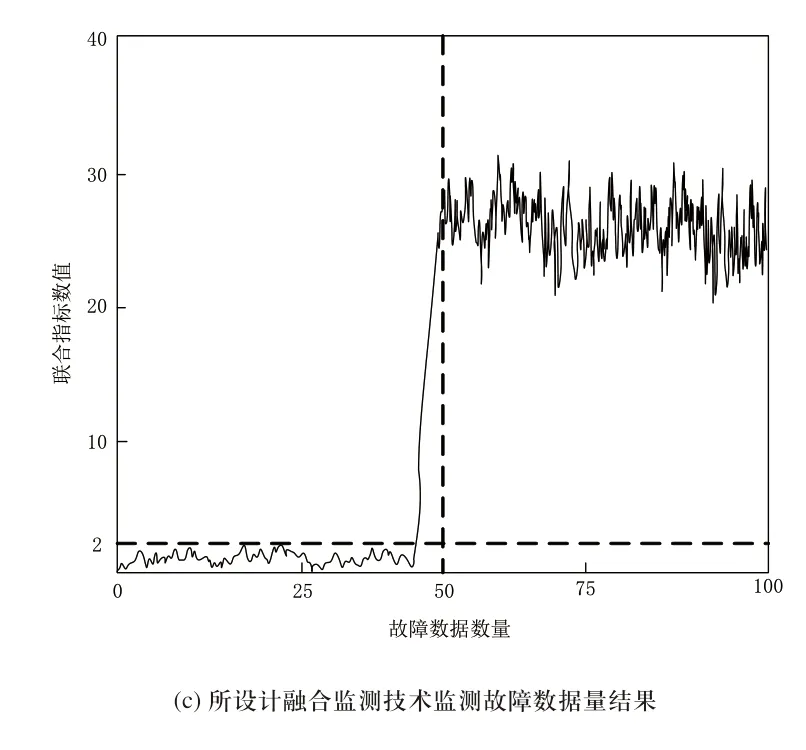
图4 三种融合监测技术监测故障融合数据量结果

根据计算得到的联合指标系数可知，三种自动化故障融合监控技术在监测故障数据时产生数值突变，可知未能监测故障时，监测技术得到的联合指标数值小于2，以该数值作为判断点，联合指标参数在20～30之间均匀变化时，表示监测技术监测得到自动化故障融合数据点。由实验设定的故障点可知，基于深度检索的融合监测技术在第16组左右的故障数据组产生联合参数突变，可知该种监测技术监测得到的故障融合数据数量为84组，对应上述设定的故障数据组数量可知，该种监测技术误将正常自动化数据监测为故障数据，该种监测技术产生了较多的误报。基于偏最小二乘的融合监测技术发生联合指标突变时对应监测得到的故障数据数量为70，可知该种监测技术监测故障数据时产生的故障漏报。而所设计的故障融合监测技术在第50组数据产生联合参数突变，根据设定的自动化故障融合数据可知，该种监测技术并未产生监测误报以及漏报，实际的监测结果最准确。

3 结语

依照海量GIS数据的处理特性，构建自动化故障融合监测技术。选定现有的两种监测技术与设计的监测技术进行性能对比，根据设定的监测测试结果反馈可知，所设计的故障监测技术能够改善监测时产生的误监与漏监问题。在未来故障融合监测过程当中，希望所构建的监测技术能够研究工作提供理论支持。