WE43稀土镁合金跨尺度蠕变时效本构关系研究

郑兴伟，袁 杰，庄 欣，赵 宗

（上海海洋大学 工程学院，上海 201306）

0 引言

蠕变时效是给一定的温度和应力的作用下材料发生缓慢变形的过程，其中伴有弹性变形、应力松弛、和时效强化的综合作用[1]。在工业技术高速发展的今天，传统材料已经不能满足航空航天的发展，在Mg合金中添加稀土元素（Y、Gd、Nd等）提高其合金的抗高温蠕变性能已成为一种发展趋势，稀土元素与合金中Mg、Zn、Zr等形成强度高的金属间化合物以实现固溶强化，析出强化，从而提高抗蠕变性能[2,3]。WE43稀土镁合金具有较好的比强度和比刚度，质量轻，同时具有良好的抗腐蚀性、抗蠕变性，抗蠕变温度可高达523K[4]。蠕变本构方程能够很好的描述材料的蠕变机理，同时也能够准确的预测在不同温度和应力下的蠕变速率和微观组织的变化规律，因此研究蠕变本构方程具有重要的意义。目前有关稀土镁合金微观组织变化的蠕变本构方程很少有文献报导。Weichen[5]研究的Mg-Al-Zn合金本构方程只考虑了一定应力和温度条件下的稳态蠕变速率的变化，而未考虑蠕变时效析出相的尺寸和体积分数对固溶强化和析出强化的影响。Manuel Carsi[6]研究的WE54稀土镁合金蠕变本构方程同样没有考虑在蠕变应力和温度下析出相的尺寸和体积分数的变化情况。但有关铝合金微观性能变化的本构方程研究相对较成熟，吕凤工[7]研究了7050铝合金蠕变时效微观组织的变化规律并构建了本构方程，李超[8]构建了7B04铝合金宏观和微观组织变化的本构方程，吕凤工和李超所构建的本构方程可以较好的描述铝合金在蠕变时效过程中析出相的尺寸和体积分数的变化规律。由于稀土镁合金的耐热性相对铝合金较差，析出相对温度的敏感性会比铝合金明显，因此在镁合金蠕变本构方程中考虑不同温度下析出相的变化情况具有一定的研究意义。本文借签铝合金蠕变时效成形本构方程的研究成果，并基于统一理论，长大动力学及析出相强化理论，构建了WE43稀土镁合金微观组织性能变化的本构方程，研究结果对稀土镁合金板材的成型及开发起到指导性作用。

1 试验方法与步

1.1 试验材料的选择

本文所采用的原材料是厚度为2mm的WE43-T5的稀土镁合金板材，主要成分和室温力学性能如表1、表2所示。本文研究的WE43稀土镁合金蠕变时效本构模型是为后续开发一种新型纤维-稀土镁合金超混杂层板的仿真研究做铺垫，考虑到超混杂层板的预浸料的固化温度区间（413K～473K）和稀土镁合金的蠕变时效成形温度区间（433K～523K）互有重叠的特性，因此本文主要关注蠕变温度为433K～473K下的蠕变性能。根据单轴拉伸试验计算出在此温度范围内最高的屈服强度为154MPa，为了既能兼顾有更好的蠕变效率又能保证试样在蠕变过程中均未被拉断，因此本文的蠕变应力选定为130MPa。

表1 WE43稀土镁合金化学成分（质量分数%）

表2 WE43稀土镁合金力学性能

1.2 蠕变试验

试验是在万能蠕变试验机上进行，蠕变试样沿WE43-T5板料轧制方向制取，按照GB/T 2039-2012标准加工的12个标准蠕变试样如图1所示，在应力为130 MPa，温度为433K、453K、473K条件下进行2.5h、5h、7.5h、10h的蠕变试验。试样加热过程中采用分段控温、分段加热，保证试样在加载过程中温度偏差在±1℃以内。试验机对试样施加恒定载荷至130MPa，在试验允许的载荷范围内手动加载，观察两侧变形值的增加速度是否一致，如果不一致反复调整引伸计，直到增速一致为止，再用引伸计测量夹具的位置，即可得到标距段伸长量，用计算机记录下数据。到规定时间点取出试样，再将试样用240#、480#、800#、1200#、2000#、3000#、5000#、7000#的砂纸进行研磨，将研磨后的试样进行抛光，抛光至光亮无划痕用酒精擦拭吹干后放在光学显微镜下观察。

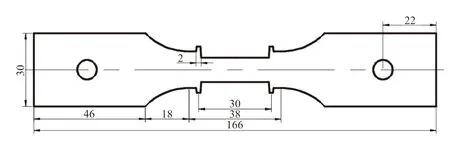
图1 WE43-T5合金蠕变试样

2 试验结果与分析

2.1 WE43稀土镁合金蠕变行为

在130MPa，433K、453K、473K温度下的蠕变曲线如图2所示，从图中可以看出温度为473K的蠕变应变量明显高于温度为433K、和453K条件下的蠕变应变量。且随着蠕变温度的升高，蠕变应变量明显增大，在蠕变开始阶段蠕变应变量迅速增大，随着时间的增加蠕变应变量趋于稳定，并达到了蠕变第二阶段，但未进入第三阶段。AZ91-Ca镁合金在温度为473K，应力为100MPa下蠕变20小时后的蠕变变形量为12.76%[9]。AZ31镁合金在温度为473K，应力为70MPa下蠕变10小时后的蠕变变形量为10%[10]。而WE43稀土镁合金在温度为473K，应力为130MPa下蠕变10小时后的蠕变变形量仅为0.04%，由此可见WE43稀土镁合金具有很好的蠕变性能。

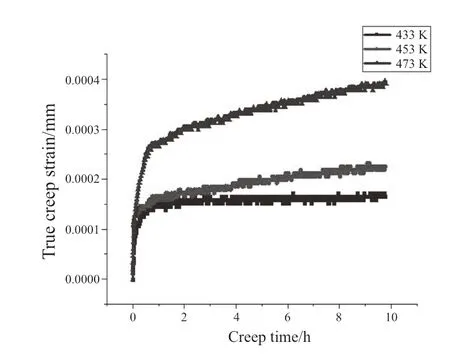
图2 130MPa 433K、453K、473K下的蠕变曲线

2.2 显微组织分析

应力为130MPa，温度为433K，453K和473K下蠕变时效7.5h后的WE43稀土镁合金试样进行XRD分析结果如图3所示，研究表明WE43稀土镁合金在该温度区间内蠕变时效过程中会析出均匀分布的Mg24Y5相和β’（Mg12NdY）相，把析出的Mg24Y5相和β’相之和作为一个整体来表示蠕变过程中析出相的变化情况。这两相之和是建立蠕变本构方程的重要变量。如图4所示析出相的大小并不是标准的球状，有些是椭圆形，为了使测量数据更加准确，规定选取最大直径方向进行测量。将得到的光学显微照片在Image-ProPlus6.0金相分析软件上完成定量分析，得到不同视野中析出相的平均尺寸和体积分数（f），为了更好的显示出析出相的尺寸和体积分数的变化规律，在构建本构方程之前需要将其进行数值化，为构建本构方程提供数据指导。

如图4所示，试样在应力为130MPa温度为453K下蠕变2.5h时析出相相对较少，随着时间增加，析出相不断变多，尺寸不断变大，当时间达到7.5h时，析出相达到最多，随后时间继续增加析出相相对减少，但析出相的尺寸是不断变大的，总体积分数基本不变。选取7.5h时的析出相体积分数为峰值体积分数（fpeak），相对体积分数（fr）定义为[11]：

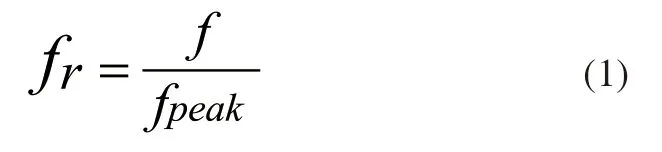
图4 蠕变应力为130 MPa，蠕变温度为453K下不同蠕变时间析出相显微形貌

图5为不同温度下，不同时间段析出相尺寸的统计结果，由图可以看出，随着蠕变时间的增加，析出相尺寸显著增加，且随着温度上升尺寸也相应的增加。这是因为随着蠕变时间的增加析出相通过自身长大及扩散来降低其界面能使之趋于稳定，且蠕变时间的增加生成的β’（Mg12NdY）相越多，温度升高β’（Mg12NdY）相生成速度越快[12]，所以析出相尺寸不断变大。由于蠕变温度接近及观察时存在一定误差，不同温度下析出相尺寸差别并不大。

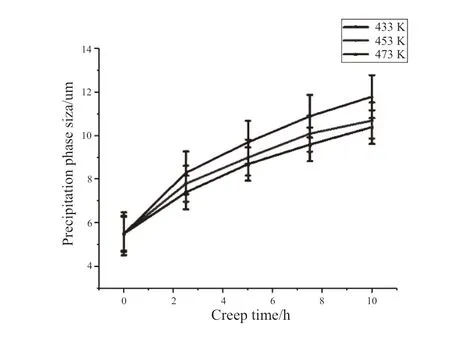
图5 130MPa 433K、453K、473K下蠕变不同时间的析出相尺寸

图6为不同温度下，不同时间段析出相体积分数的统计结果，由图可以看出析出相体积分数先增加随后相对减少。且开始阶段的增加速度明显高于后期，这是由于蠕变开始阶段生成的β’相不断增多，但随着蠕变时间的增加，少量Mg24Y5相溶解在Mg基体中[13]。

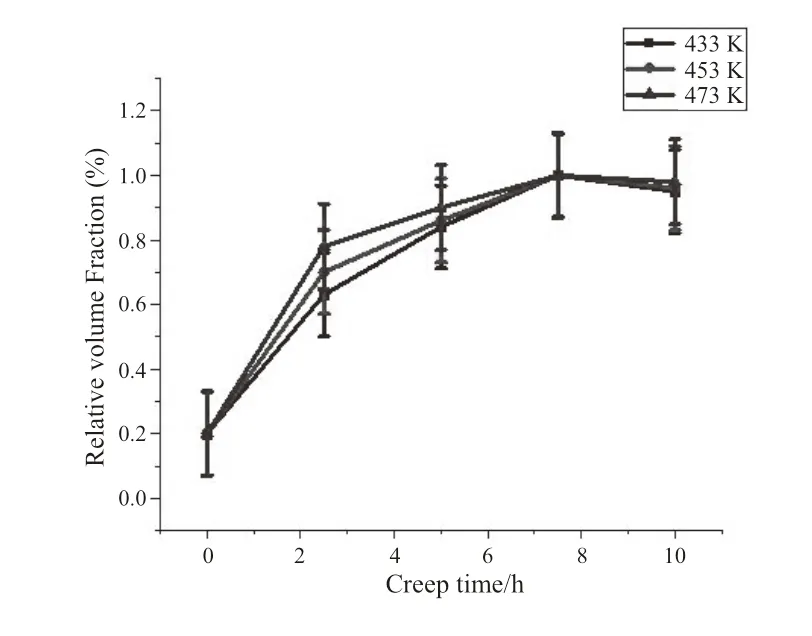
图6 130MPa 433K、453K、473K下蠕变不同时间的析出相相对体积分数

3 本构模型的研究现状及构建

3.1 本构模型的研究现状

目前国内外广泛应用的镁合金蠕变本构模型有指数函数模型（power-law方程），双曲正弦模型，分别以下表示：

1）指数函数模型

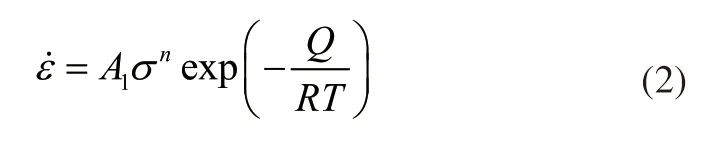
式中，σ为应力，n为应力指数，A1为材料常数，Q为热激活能，R为气体常数，T为绝对温度

合金的稳态蠕变速率满足power-law方程[14]，此本构模型能描述镁合金的蠕变机理和稳态阶段温度和应力对蠕变速率的影响，但没有考虑第一阶段温度和应力对蠕变速率的影响，同时也没有考虑材料在高温下的析出相变化对蠕变速率的影响。

2）双曲正弦模型

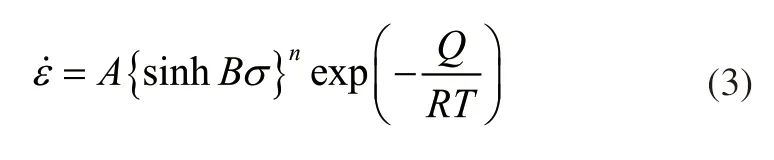
式中，A、B为材料常数，σ为应力，n为应力指数，Q为热激活能，R为气体常数，T为绝对温度。

双曲正弦模型考虑了蠕变第一阶段和稳态阶段应力和温度对蠕变速率的影响，但同样没有考虑蠕变时效过程中析出相的尺寸和体积分数对蠕变速率的影响。

Stefano Spigarelli[15]基于双曲正弦模型并引入了阀值应力和弹性剪切模量建立了如式(4)所示的本构方程，该本构方程能很好的描述镁合金蠕变微观组织的变化规律。

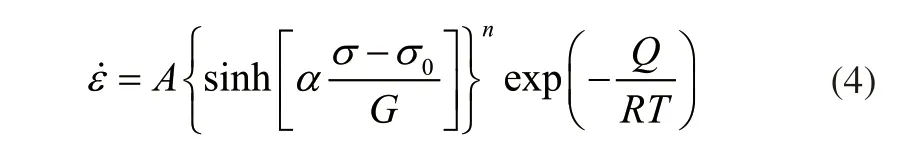
式中，A、α为材料常数，G为弹性剪切模量，σ为应力，σ0为粒子位错产生的阀值应力，n为应力指数，Q为热激活能，R为气体常数，T为绝对温度。

3.2 本构模型的构建

由于WE43稀土镁合金在应力为130MPa温度为433K、453K、473K下会析出Mg24Y5相和β’（Mg14Nd2Y）相，这两相钉扎作用在晶界上阻碍位错的滑移，为了便于研究做了以下几点假设[16]：1）析出相的形核、长大及相变是相互独立的；2）析出相的形貌和位错在各个过程中是保持不变的；3）蠕变内应力和温度是原子运动改变系统能量的主要原因。

如图2蠕变曲线所示，在应力为130MPa，温度为433K、453K、473K下蠕变10h材料没有进入第三阶段，所以只需考虑蠕变第一、第二阶段特性。由于稀土镁合金与铝合金析出相的机理、位错与析出相的相互作用是相似的，所以描述铝合金微观组织性能的本构方程同样也适用于WE43稀土镁合金中。Z.L.Kowalewski等[17]引入蠕变状态变量提出单轴受力条件下的蠕变本构方程，经必要的修正后得出[18]：

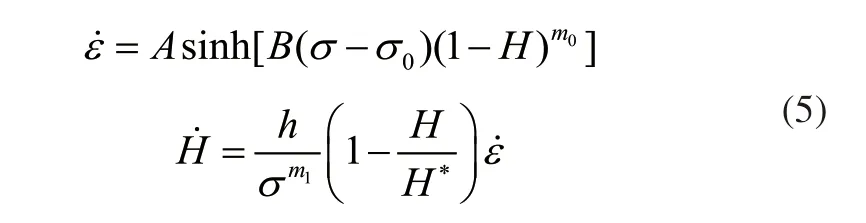
方程(5)构建的蠕变本构方程能够很好的描述温度一定的条件下，不同应力对材料蠕变应变率的影响，而式(4)构建的蠕变本构方程充分考虑了温度的影响，结合式(4)和式(5)经必要的修正得到能够描述应力一定条件下不同温度对材料蠕变应变率影响的本构方程即：

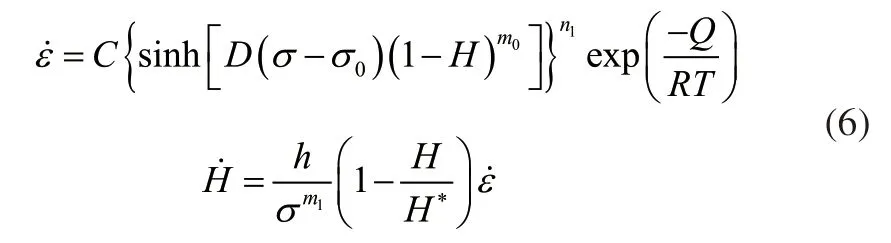
式中，C、D为材料常数，σ为应力，n1为应力指数，Q为热激活能，R为气体常数，T为绝对温度。

人工时效强化合金的综合强化来自固溶强化，析出强化和合金的固有强度，WE43稀土镁合金的固溶强化可以表示为[19]：

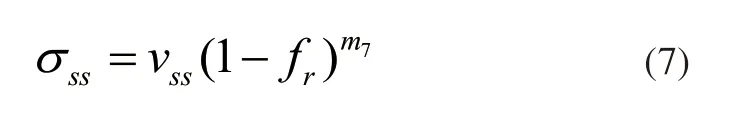
式中，vss和m7为材料常数。

在蠕变时效过程中析出相对位错的钉扎使得屈服强度发生变化，从位错与第二相粒子的交互作用确定材料的临界剪切应力，可以得到析出强化的表达式即[20]：

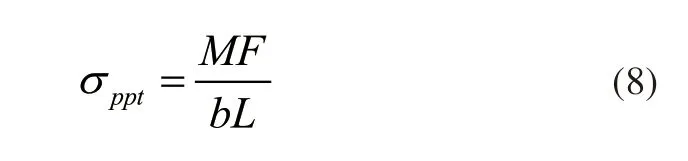
式中，F为平均障碍强度；L为沿位错线的平均析出物颗粒间距；M为泰勒常数；b为柏氏模量.析出相对位错的阻碍强度与析出相半径呈指数关系[20]即：

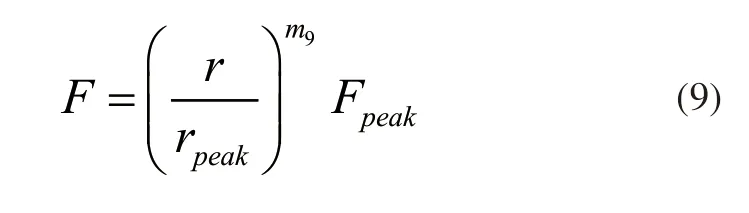
式中，m9为材料常数，rpeak为峰时蠕变条件下析出相的平均半径，Fpeak为峰时蠕变条件下析出相与位错的平均交互作用力。

因为WE43稀土镁合金的析出相近似为球状，根据J.F.Nie等[21]研究结果得到平均析出物颗粒间距的方程即：

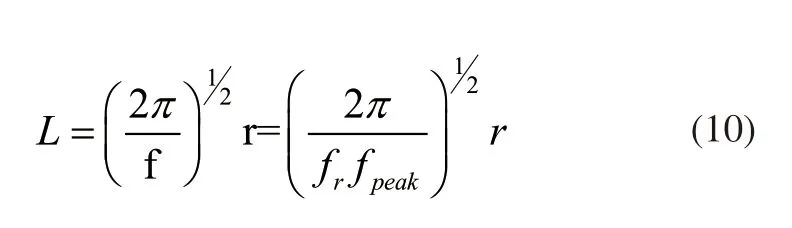
将式(9)、式(10)代入到式(8)中可得析出强化与析出相尺寸和体积分数的关系即：

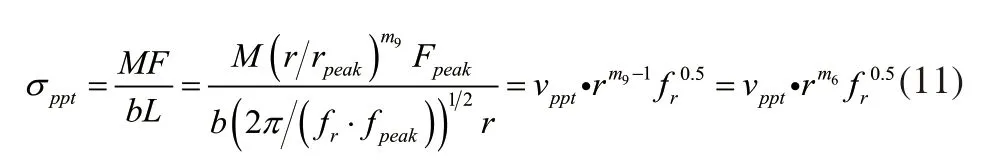
由于固溶强化和析出强化对蠕变速率也有很大的影响，为了保证蠕变本构方程的准确性，对式(6)进一步修正后得：

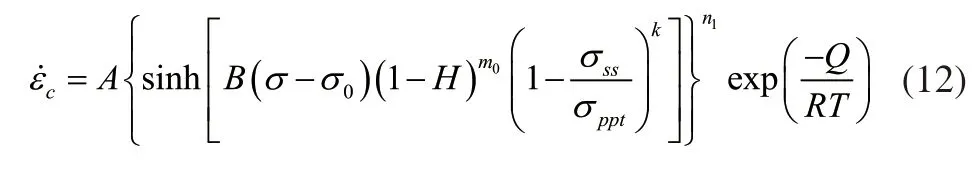
将式(6)、式(7)、式(11)、式(12)联立即可得到能够描述WE43稀土镁合金跨尺度蠕变时效本构方程即：

式中，A、B、m0、k、h、m1、Vr、m2、J、m3、Vf、m4、m5、Vppt、m6、Vss、m7为材料常数，σ为应力，σ0为粒子位错产生的阀值应力，n1为应力指数，H为状态变量，H*为H的饱和值，Q为热激活能，R为气体常数，T为绝对温度。

WE43稀土镁合金在蠕变时效过程中发生固溶强化、析出强化，析出的第二相钉扎在晶界上对蠕变速率有很大的影响，本文构建的本构方程充分考虑到了蠕变时效过程中析出相的固溶强化和析出强化对蠕变速率的影响，同时也能够描述析出相的尺寸和体积分数的变化规律。

4 本构方程参数拟合优化

本构方程中含有22个材料参数，传统的最小二乘法拟合已经难以实现，因此采用遗传算法求解优化目标函数的最小值[22]，从而确定本构方程中各个材料常数的取值。在跨尺度本构模型中，由于物理量之间的单位不同，相互之间不具有可比性，因此本文将相关物理量无量纲化[23]即省去各物理量之间的单位，采用计算曲线与试验曲线达到相同数据点的时间差作为标准来构造目标函数，建立目标函数[22,24]即：

遗传算法的拟合在MATLAB工具箱中进行，先给定一组数值，对式(13)进行4阶RK算法求积分，再把达到相同数据点计算值与试验值的时间差作比较，时间差最小即为一组最优解，最优的材料参数如表3所示：

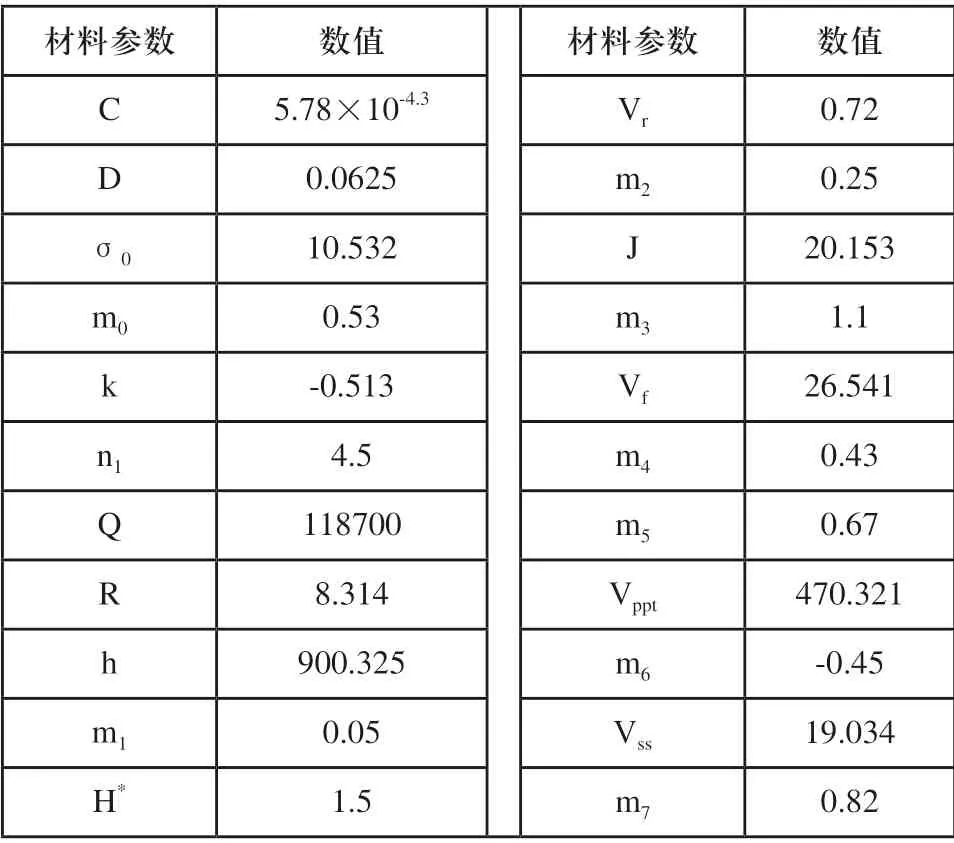
表3 WE43稀土镁合金本构方程材料参数

将遗传算法拟合的参数代入到方程(13)，得到本文所构建的具体本构方程如下：

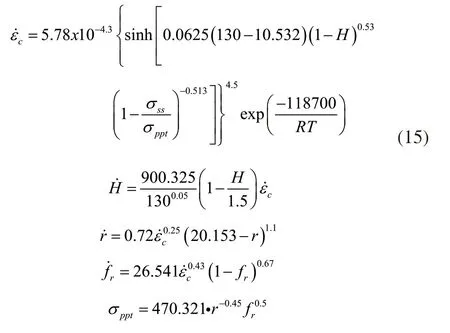
图7为蠕变应变量的拟合结果。从图中可以看出蠕变应变量的计算值和试验值拟合存在一定误差，误差来源可能因为所取温度的区间相对较小，且统计数量有限。但蠕变速率计算值与试验值的变化规律是一致的。

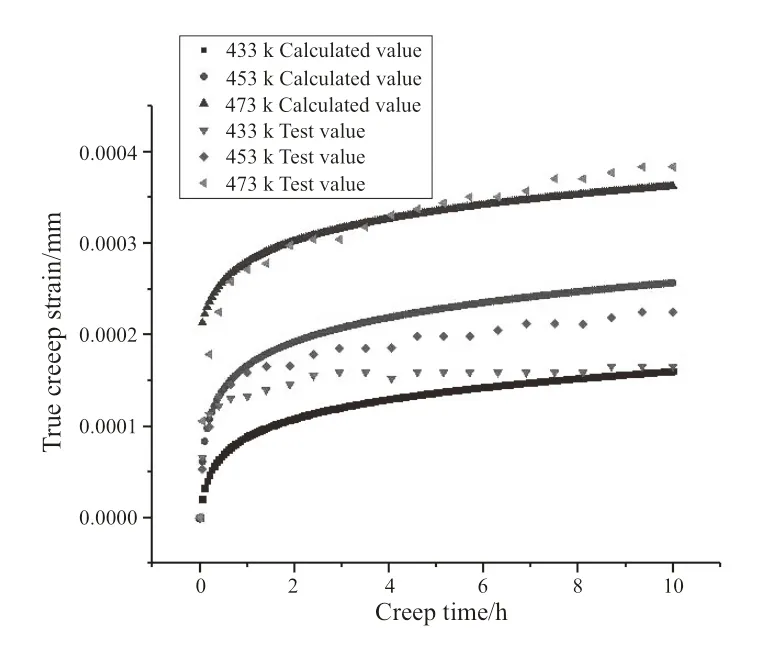
图7 130MPa 433K、453K、473K下的蠕变应变量计算值与试验值

图8和图9所示的是析出相尺寸、相对体积分数的计算值和试验值的拟合图。可以看出析出相尺寸和体积分数的计算值与试验值有很好的拟合度，这说明可以通过本文所构建的本构方程去预测不同蠕变工艺条件下析出相的变化情况，但拟合曲线也存在一定的误差，误差来源可能因为本文构建的本构方程是对实际情况一定简化的前提下进行，或者是用Image-ProPlus6.0软件观察并测量析出相尺寸和体积分数时存在一定误差。

图8 130MPa 433K、453K、473K下的析出相尺寸计算值与试验值

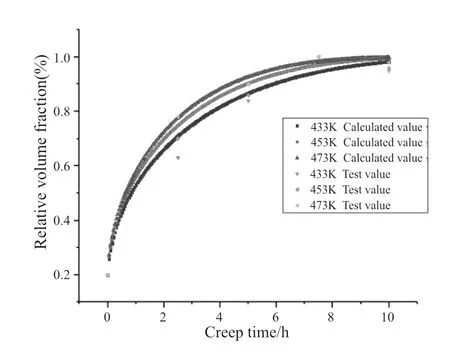
图9 130MPa 433K、453K、473K下的析出相体积分数计算值与试验值

5 本构方程的验算

本构方程中的蠕变应变、析出相尺寸和体积分数的计算值与试验值误差百分比可以用式(16)表示，平均误差可以用式(17)表示。

根据式(16)和式(17)，本文构建的本构方程，在温度为433K、453K、473K下，蠕变应变量的误差分别为14.8%、8.4%、4.35%，平均误差为9.18%；析出相尺寸的误差分别为4.24%、4.52%、5.55%，平均误差为4.77%；析出相体积分数的误差分别为5.97%、4.07%、1.6%，平均误差为3.88%。

6 结语

本文主要做了WE43稀土镁合金在不同时间段的蠕变试验，通过光学显微镜观察其蠕变时效后析出相的尺寸和体积分数的变化规律，并借签于铝合金比较成熟的析出相本构模型得出了以下结论：

1）WE43稀土镁合金在应力为130MPa温度为433 K、453K和473K下，随着蠕变时间的增加析出相尺寸相应的增加，体积分数出现先增加后相对减少，但随着蠕变温度的提升，析出相尺寸和体积分数都出现明显的增加。

2）构建了WE43稀土镁合金跨尺度蠕变时效本构方程，该本构方程考虑了析出强化、固溶强化对蠕变应变率的影响，同时能够预测析出相的尺寸和体积分数的变化规律。