基于线驱动原理的3T1R并联机器人运动参数分析

焦迎雪，聂秀珍

（山西铁道职业技术学院，太原 030013）

0 引言

科学技术的发展，给生产活动带来的新的发展动力，传统生产活动的进行主要通过人力来完成，当面对大型生产活动时，人力生产不仅效率低，质量也相对较低，无法达到高精度的程度，更重要的是危险的生产活动会给人们的生命安全带来威胁。在此背景下，科学技术的发展使得生产活动逐渐向着智能化、自动化和机械化方向发展，其中机器人是出现和使用就是自动化生产的典型代表。3T1R并联机器人是现代化生产中最常用的一种。3T1R并联机器人，即三平移一转动机器人，具有刚度强、速度快、承载能力强等优点，在分拣、搬运、上下料、定位装配等领域发挥了重要的作用[1]。通过应用领域可知，该类机器人对运动参数的控制要求较高。

关于并联机器人运动参数的分析方法有很多，如基于模糊理论的方法，该方法通过模糊推理将控制量转化为控制输出，为机器人提供运动参数。这种方法不需要建立精确的控制模型，且鲁棒性较强，但是面对精细化程度较高物体，得出的控制参数精准度不够。基于PID的方法。这种方法的控制精度较高，但是适用性不强，其得出的控制参数只适用其对应的物体操作控制，而且其参数需要整定。

结合前人研究经验，针对以往控制方法存在的缺点，提出一种基于线驱动原理的3T1R并联机器人运动参数分析方法。该方法以线驱动原理为基础，通过明确线性驱动器输出量与3T1R并联机器人运动参数之间的线性关系来获取运动数值。最后将该分析方法应用到一个3T1R并联机器人运动控制当中，检验运动参数与预期参数之间的误差，以此分析得出分析方法的精度。通过本研究以期提高3T1R并联机器人工作质量[2]。

1 3T1R并联机器人运动参数分析方法

3T1R并联机器人是一种自由度较高的智能机器人，主要用于分拣、包装、上下料、搬运等工作当中。3T1R并联机器人由动平台、静平台、无约束支链、混合支链、控制器以及驱动器组成。在3T1R并联机器人整个工作过程中，通过控制器推算得出3T1R并联机器人的运动参数，然后以此控制线性驱动器驱动机械手/臂完成抓取、移动、投放等动作。由此可知，3T1R并联机器人运动参数的推算工作至关重要，推算的越准确，3T1R并联机器人的动作精度越高。基于此，提出一种基于线驱动原理的3T1R并联机器人运动参数分析法。

1.1 线性驱动器运行参量采集

3T1R并联机器是在线性驱动器的驱动下执行相关动作的，因此线性驱动器与3T1R并联机器之间存在很明显的线性关系，即一方发生改变，另一方也随之发生改变的现象。线性驱动器，也被称为交流伺服驱动器，主要负责3T1R并联机器人三个参数的控制，即运动速度、运动位置以及运动力矩[3]。这三个控制量的采集就是后续3T1R并联机器人运动参数得出的关键。基于此，参数的获取首先要对线性驱动器的三个参量进行采集。

目前，基于现有的技术，传感器采集是最常用的手段。根据需要采集的参量的不同，选择的传感器类型为位移传感器、速度传感器以及电流互感器。这些参量采集到之后，转换为数字信号，这些数字信号受到采集环境以及传感器本身影响，其信号中会存在大量的噪声，影响了后期运动参数推算结果的准确性。为此，需要对这些噪声进行去除。在这里采用一种混合的去噪方法进行去噪，该方法中包括了三种方法，即独立分量分析法、经验模态分解法以及小波阈值去噪方法。该方法具体过程如下：

步骤1：将包含噪声数字信号a划分为m个频段；

步骤2：对m段信号进行平移拼接；

步骤3：将平移拼接处理后的m维信号作为独立分量分析的输入通道信号；

步骤4：利用独立分量分析法对信号进行盲源分离，得到初步去噪信号。

步骤5：将初步去噪信号进行经验模态分解，分解公式如下：

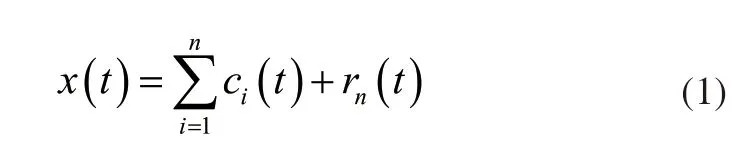
得到n个IMF分量和1个残差rn（t）。其中，c（t）被称为IMF分量。

步骤6：源信号主要集中在第1个和第2个IMF分量当中，因此只保留这两个IMF分量。

步骤7：利用小波阈值法对第1个和第2个IMF分量进行去噪。具体过程如下：

step1：利用小波变换将IMF分量变换到小波域，得到小波分解系数；

step2：利用选择的阈值函数对小波分解系数进行处理，得到小波估计系数。阈值函数形式如下：

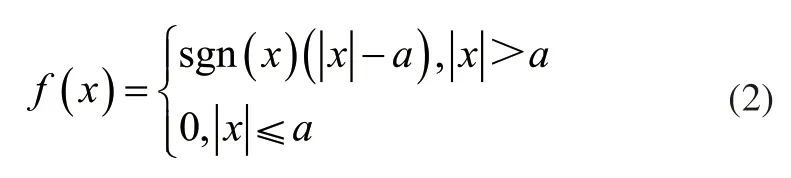
式中，sgn（）代表符号函数；a代表阈值；x代表信号。

step3：选择小波分解系数与小波估计系数相减绝对值的最小值；

step4：进行小波重构，得到去噪后信号。

1.2 3T1R并联机器人数学建模

本章节为方便后续分析与计算，本章节建立关于3T1R并联机器人数学模型。该模型建立的主要通过Matlab软件当中的Simulink工具来进行，建模过程如下：

步骤1：登录Matlab软件，选择Simulink工具模块；

步骤2：启动Simulink工具；

步骤3：画出3T1R并联机器人的各个组成模块；

步骤4：在组成模块上添加3T1R并联机器相关参数；

步骤5：根据各个模块之间的连接关系，画出所有模块之间的连接线；

步骤6：指定输入、输出端子。

基于建立好的3T1R并联机器人数学模型，即可投入使用。开始时，模型设定初始状态和输出，接下来的每一个时间步中，Simulink计算并联机器人的输入、状态和输出，并更新模型来反映计算出的值。结束时，模型得出相应的输入、状态和输出[4]。

1.3 3T1R并联机器人运动参数计算

基于上述两个步骤的研究，接下来进入最后关键的一步，计算3T1R并联机器人运动参数。在这里需要利用改进后的PID算法来进行。

PID算法的计算能力是实现线性驱动器与3T1R并联机器人线性连接的关键，主要通过PID的比例、积分、微分计算，推算出3T1R并联机器人运动参数。PID工作原理是通过线性驱动器实际输出和预期输出之间误差，在比例、积分、微分的运算下，得出3T1R并联机器人运动参数。

线性驱动器实际输出和预期输出之间误差计算公式如下：

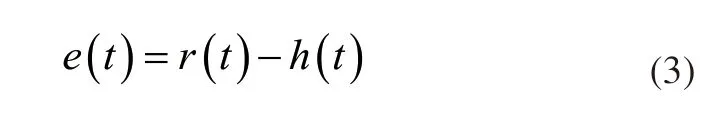
式中，e（t）代表误差；r（t）代表线性驱动器预期输出；h（t）代表线性驱动器实际输出。

根据e（t）进行比例、积分、微分计算，得出3T1R并联机器人运动控制参数。计算公式如下：

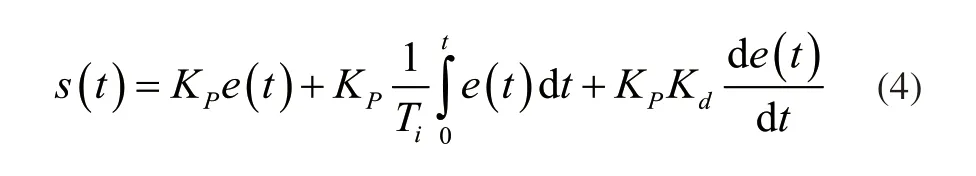
式中，s（t）代表PID输出的并联机器人运动控制参数；KP、Kd分别代表比例、积分以及微分系数；Ti、Td代表积分时间常数和微分时间常数。

将上述公式(4)进行离散化处理，得到：

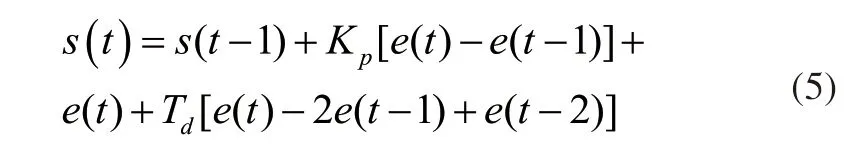
3T1R并联机器人运动的准确性与PID计算结果有着直接关系，而影响PID计算结果的关键在于比例、积分、微分三个参数整定[5]。一个3T1R并联机器人完成一次作业任务，需要其机械手/臂的运动参数不断进行改变，才能使其具有灵活性。但是传统PID推算结果只适用于一种动作的控制，要想计算其他动作，就需要重新进行推算，效率较慢，且精度也不能保证，因此需要对PID的三个参数进行整定，调高其灵活性和适用性。

PID整定方法有很多，如蚁群算法、模拟退火算法、遗传算法等。这些方法各有优缺点，如表1所示。

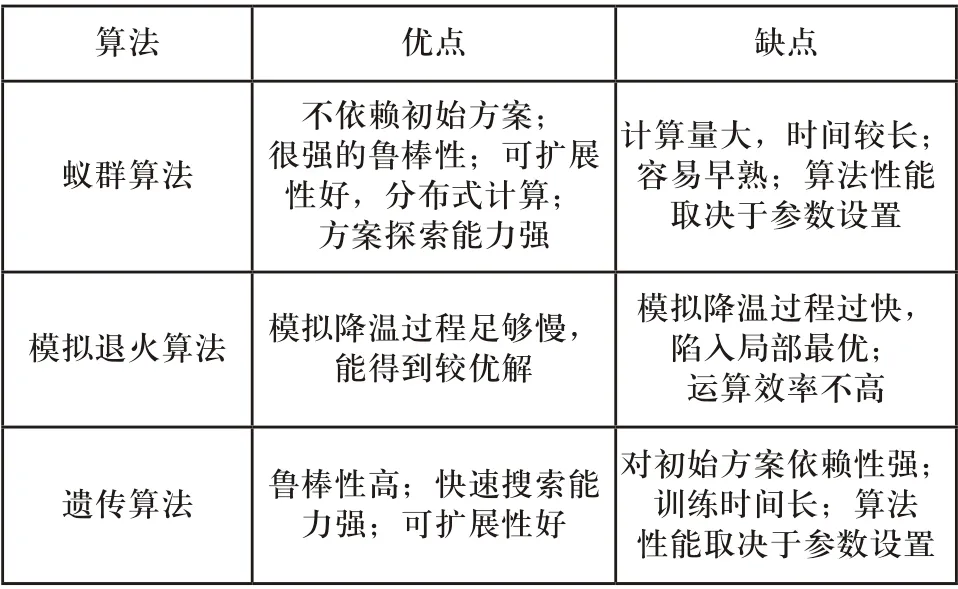
表1 PID参数整定方法优缺点

以上述遗传算法为基础，利用细菌共轭算子进行优化，然后利用优化后的算法对PID三个参数进行整定，具体过程如图1所示。

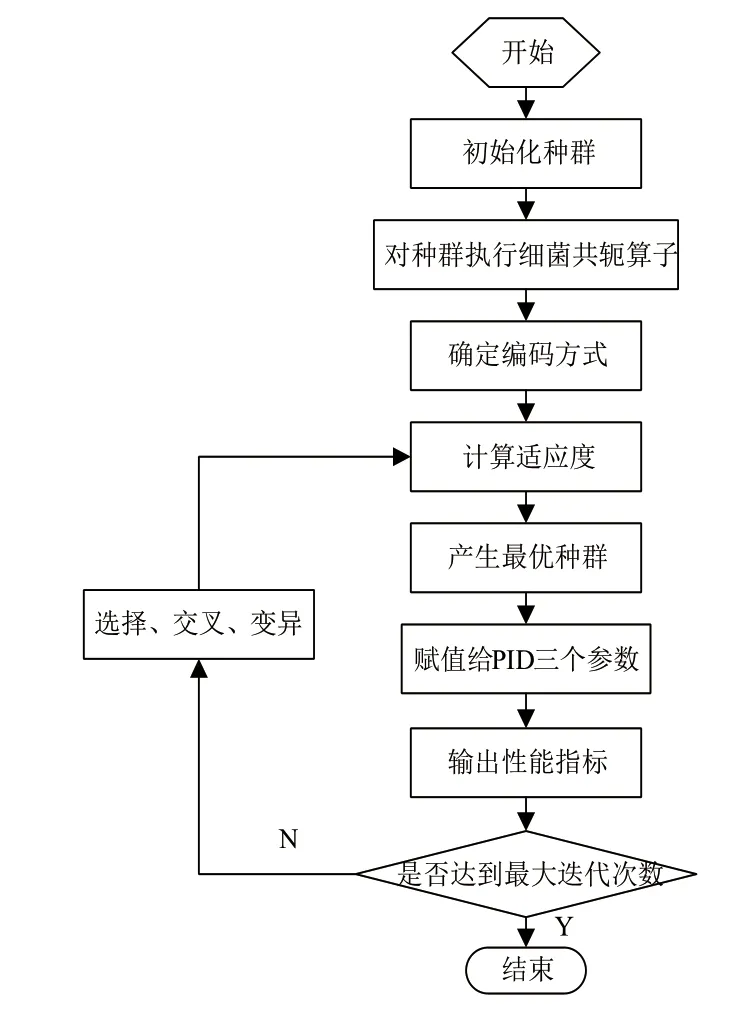
图1 PID参数整定流程

2 测试与分析

为测试所研究分析方法在3T1R并联机器人运动参数计算中的应用效果，以MATLAB软件为平台，进行测试。

2.1 设备选择

本测试中，将所选择的3T1R并联机器人用于分拣作业当中。通过分拣作业的完成效果来检验其运动参数分析质量。所选择的3T1R并联机器人本身工作参数如下：

1）机械臂自由度：3自由度+夹持器；

2）有效负载：200g（伸直可夹重量）；

3）负载：500g（夹持搬运重量）；

4）臂展：350mm；

5）有效抓取范围：半径≤30cm；以中心轴为半圆的区域；

6）抓取物体直径：1cm～6cm；

与之相连的为线性驱动器，本测试中所选择的线性驱动器的关键参数如下：

1）丝杠导程mm：5；

2）电机功率w：400；

3）电机额定转速rpm：3000；

4）减速比额定出力kN：1；

5）额定速度mm/s：250；

6）额定行程mm：300。

2.2 传感器采集线性驱动器运行参量

利用位移传感器、速度传感器以及电流互感器采集所选择线性驱动器运行参量，采集过程如图2所示。

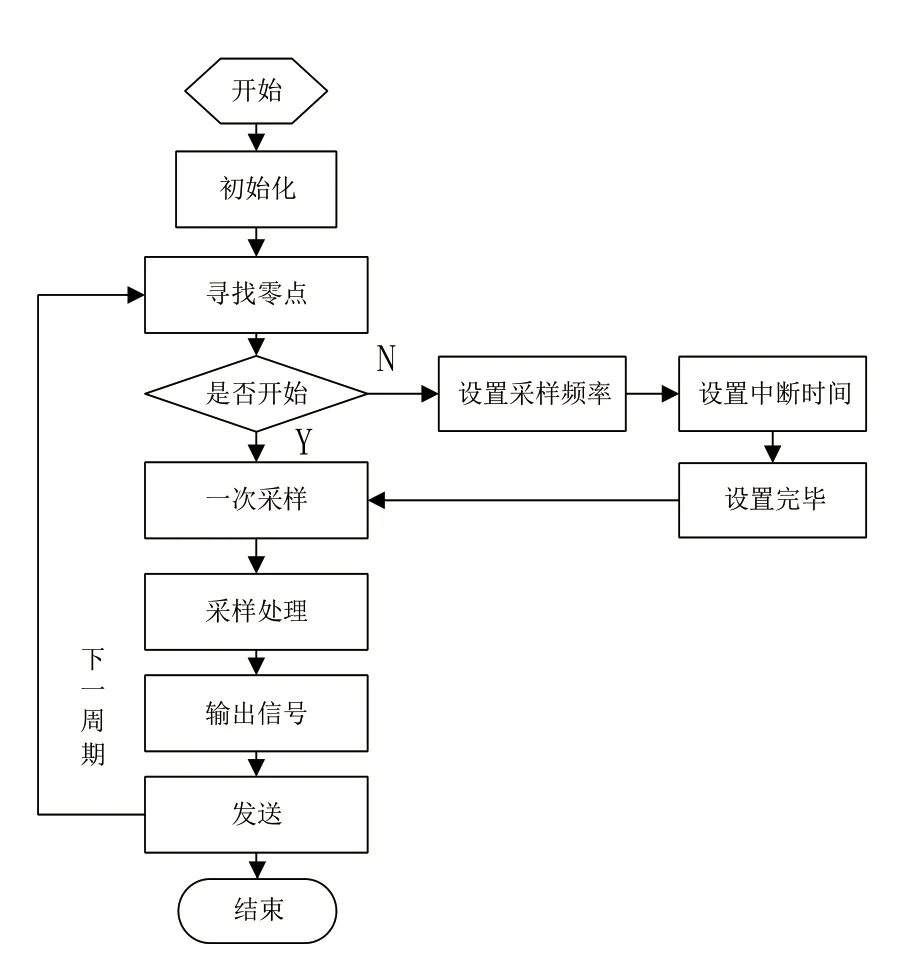
图2 感器采集线性驱动器运行参量程序

2.3 3T1R并联机器人运行模型

利用MATLAB中的Simulink，按照章节1.2，建立3T1R并联机器人运行，如图3所示。

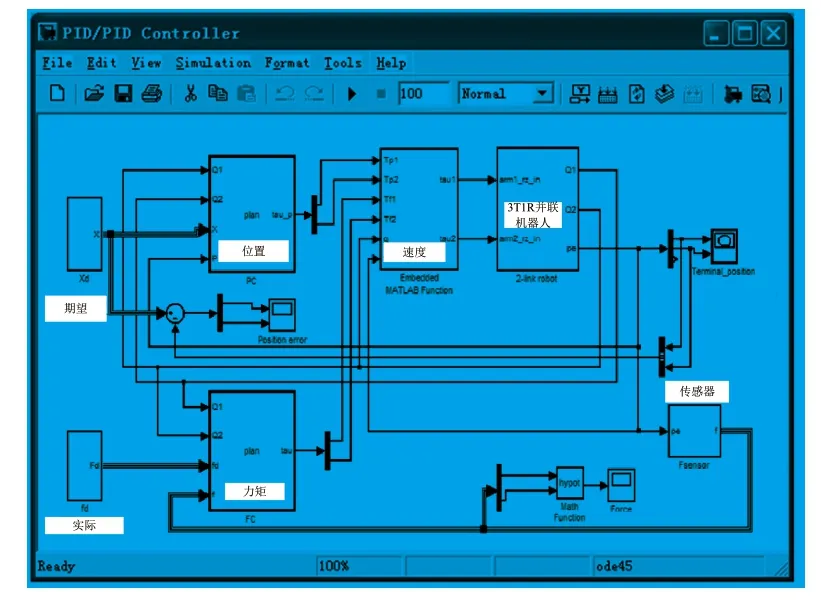
图3 3T1R并联机器人运行模型

2.4 作业现场搭建

以直径为4mm的小型药片为分拣对象，结合3T1R并联机器人搭建作业现场，如图4所示[6]。

图4 3T1R并联机器人作业现场

2.5 运动轨迹设定

利用3T1R并联机器人将小型药片分拣到不同类别的储存罐当中，分拣理想运动轨迹如图5所示。

在图5中理想运动轨迹每个阶段选择一个时间点，其对应当中3T1R并联机器人的理想运动参数如下：

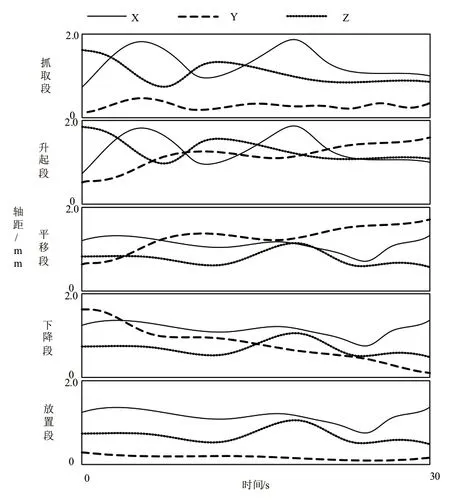
图5 3T1R并联机器人分拣理想运动轨迹

抓取段：位置（0.52，1.32，0.44）；速度：1.25cm/s；力：4.68N：

升起段：位置（1.72，1.21，1.34）；速度：1.22cm/s；力：5.63N：

平移段：位置（1.57，1.02，1.41）；速度：2.14cm/s；力：6.32N：

下降段：位置（0.51，0.32，0.32）；速度：1.15cm/s；力：3.32N：

放置段：位置（0.56，0.03，0.25）；速度：1.00cm/s；力：0.02N：

2.6 算法参数设置

遗传算法整定PID参数时，算法运行初始参数如下：

1）群体大小：30；

2）遗传算法的终止进化代数：200；

3）选择概率：0.25；

4）交叉概率：0.50；

5）变异概率：0.0025；

6）PID控制三个参数的寻优范围：[0，100]。

2.7 效果分析统计与分析

相同测试条件下，应用基于模糊理论的分析方法和基于PID的分析方法，以此进行分拣作业，然后同样一个时间点，统计3T1R并联机器人运动参数，得出实际运动参数，并与理想运动参数进行对比[7]。结果如表2所示。

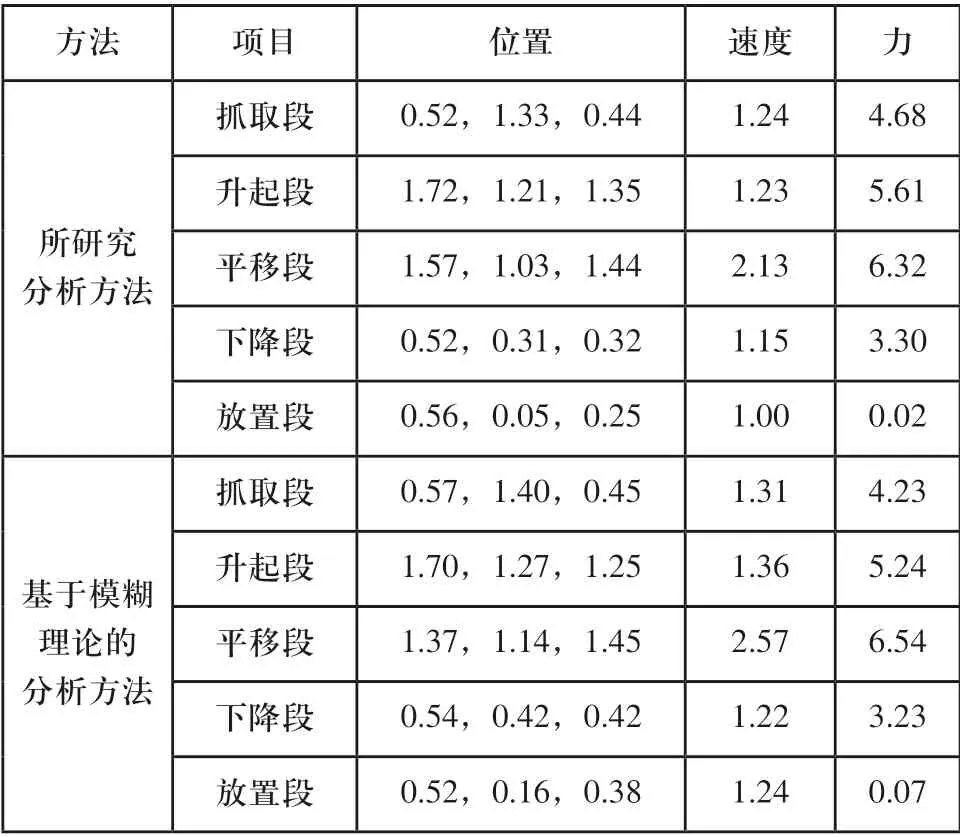
表2 3T1R并联机器人实际运动参数

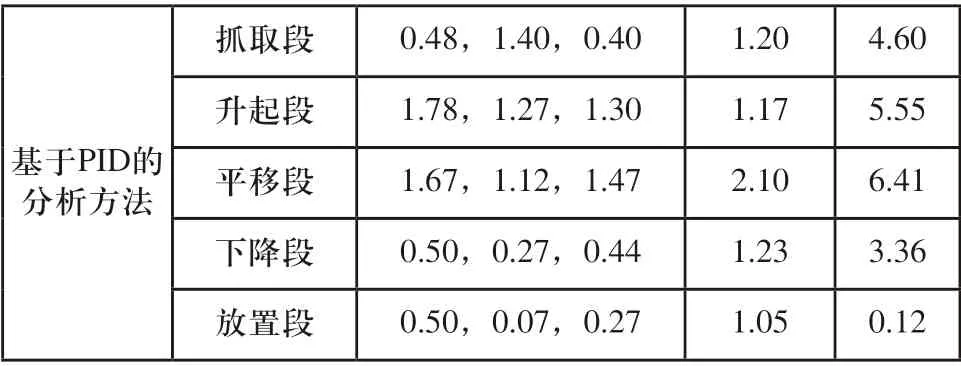
表2 （续）

将表2中的实际运动参数与2.5章节中3T1R并联机器人的理想运动参数进行对比，从中可以看出：以其他两种方法相比，所研究方法应用下，理想运动参数与实际运动参数更为相近，说明所研究方法分析质量更高，得出的运动参数精度更高[8]。

3 结语

综上所述，为提高生产效率和质量，降低其生产过程中的风险，并联机器人常被应用到现代化生产当中。然而，随着作业对象的更精细化，对其运动参数精度要求更高。为此，进行基于线驱动原理的3T1R并联机器人运动参数分析。最后通过实际应用，测试分析方法的精确度，得出理想运动参数与实际运动参数更为相近，证明了方法的有效性。然而，本研究，仅在理想的环境中进行测试，与实际应用情况存在一定的差别，因此有待进一步分析和探讨。