排放控制区下集装箱班轮航线路径规划与航速调度集成决策

楚金华，李俊鹤，王春娟，陈超

(山东交通学院，a.国际商学院；b.航运学院，山东威海264200)

0 引言

集装箱班轮运输，是开展海上清洁运输的重要领域。在排放控制区和“限硫令”实施背景下，班轮公司采用燃料转换策略，依据燃油价格差异，合理确定船舶在排放控制区内外航行距离、设定相应航速，安排挂港次序，不仅有利于控制尾气排放，降低环境污染，同时还有助于降低运营成本，优化航线路径，探索路径规划与航速调度集成决策的问题特点和建模方法。

集装箱班轮航线，具有船舶挂港数量多、定期往返频繁、在航效率高的特点，受沿海排放控制区和“限硫令”实施的影响尤为明显。对于大多数集装箱船来说，在尚未安装脱硫塔装置和天然气设备时，采用燃料转换策略，即区内使用轻质柴油(硫含量低于0.1%)、区外使用低硫燃油(硫含量低于0.5%)，已成为当下航线适应排放控制区和“限硫令”要求的必然选择。在这一策略下，为了控制船舶尾气排放污染，港口间航行区域将被划分为离港控制区、非控制区和进港控制区，船舶航迹有可能从以往的“直线”，改为“折线”。显然，这种船舶“折线”航迹的长度，将随控制区内外油价差异变化而变化。油价差异越大，航迹则应越长；油价差异越小，航迹则应越短。船舶航迹长度的如此变化，必然会对耗油和耗时产生影响。当控制区内油价相对越高，航迹应相对越短，对应航速应越低，油耗虽会减少，但时耗会增加；而控制区外油价相对越低，航迹应相对越长，对应航速应越高，油耗虽会增加，但时耗会减少。这种不同油价差异下的不同“折线”构成，对相应航速提出不同要求，在对港口间运营费用产生作用的同时，也对港口间OD对组合产生影响，导致航线挂港次序变化。由此可见，在这种情况下，根据油价差异变化，合理确定船舶在港口间的“折线”构成，优化“折线”航速，安排挂港次序，优化航线路径，无疑已经成为当下集装箱班轮公司进行航线规划运营调度决策面临亟待解决的棘手问题。

目前，有关排放控制区下集装箱班轮航线的研究较少。Fagerholt[1]等提出船舶进出排放控制区轨迹的折射点概念，运用勾股定理构建确定折射点的优化模型，并利用敏感度分析阐述了排放控制区内外燃油价格差异对船舶在区内外航行轨迹及相应航速的影响。Yewen Gu[2]等研究了两种降硫技术(脱硫系统与燃料转换)的评价与选择，考虑了船舶航速与路径选择的影响，构建了寿命周期成本的数学规划模型。Li L.Y.[3]等构建了混合整数非线性规划模型，获得了包含ECA进出点、内外航速和航行轨迹的最优航行方式，并研究了航行方式优化对污染排放和燃油成本的影响；Zhen L.[4]等研究了在燃料转换策略下，对各港口间诸多可行路径，构建航迹组合选择模型，设计禁忌算法，并通过美国东南沿海邮轮航线，验证了模型的有效性。王春娟[5]等研究了不同加油港油价差异下，加油补给选择问题，构建了燃油补给选择与航段航速优化集成调度模型；Wang S.A.[6]等研究了排放控制区燃油价格差异下，班轮运营计划问题，分别从航速与路径规划、船队部署以及班期设定等方面建立模型，并设计相应优化算法。

与上述相关研究不同，本文基于Fagerholt提出的折射点概念和建模方法，引入船舶进出港射角的概念，即由港口至距其控制区外沿最近点形成直线与港口至船舶进出控制区外沿任意点形成直线的夹角，并运用斜边非限定变异三角函数几何方法，构建射角与港口间控制区内外航距组合关系模型。在此基础上，考虑轻质柴油与低硫燃油价格比值变化与控制区内外航距组合之间的效用关系，船舶航速对耗油费用和耗时费用产生的悖反关系，耗油费用与耗时费用对航线挂港次序的决定关系，以及这些关系相互影响、相互作用、相互耦合，共同对航线运营成本产生的影响，提出排放控制区下集装箱班轮航线路径规划与航速调度集成决策问题。并将该问题视为一类变异的TSP问题，构建一个以进出港射角、控制区内外航速、航线挂港次序为决策变量，以航线运营总成本最小为目标的两阶段集装箱班轮航线路径规划与航速调度集成决策模型，设计相应启发式算法，并通过案例应用与数据分析，验证该模型构建和算法设计的有效性和实用性。

1 问题描述

排放控制区下集装箱班轮航线运营，与常规班轮航线不同。它要求船舶在港口间航行，首先从某一个挂靠港口出发，经过沿岸排放控制区航行后，再进入非排放控制区航行，完成非控制区航行后，再进入另一端沿岸排放控制区航行，最后抵达下一挂靠港口。在这个过程中，船舶航行轨迹由3段构成，即出港控制区段、非控制区段、入港控制区段。由此3段构成的船舶航行轨迹，将使两港间以往的“直线”航段，变成“折线”航段。图1(a)～(d)为不同港口区位下“折线”航迹。“折线”组合长度与组合比例，可用船舶进港射入角和离港射出角表示，如图2中θi、θj。受船舶在排放控制区内外消耗燃油价格差异影响，轻质柴油与低硫燃油的价格差异越大，射入角和射出角就越小，即航行轨迹的“折线”越明显；反之，轻质柴油与低硫燃油的价格差异越小，射入角和射出角越大，即航行轨迹的“折线”越不明显，当轻质柴油与低硫燃油价格相同时，即航行轨迹的“折线”变成了“直线”。如图1所示，虚线表示最大射角的“折线”，实线表示最小射角的“折线”，α1、α2为进出港射角的范围。显然，船舶实际航行轨迹通常处于实线与虚线之间。

图1 港口和控制区的位置及进出港射角取值范围Fig.1 Position of different ports and ECAs and angle range of port-entry and port-exit

根据排放控制区下集装箱班轮航线运营特点，为降低船舶耗油费用，减少航次运营时间，保证班轮航线班期要求，提高航次运营效益和效率，航线规划与航速调度集成决策需要面对诸多影响因素。一方面，根据控制区内外燃油价格的差异，选择船舶进出港射角，确定船舶在控制区内外的航行距离，控制好港口间船舶航行的总距离。协调好船舶在控制区内外航距的悖反关系，并通过构建在不同射入角和射出角下控制区内外航距比例关系函数，进行平衡约束。另一方面，结合航速与燃油消耗和航行时间的关系，合理设定控制区内外的航速。协调好航次耗时费用与耗油费用之间的悖反效应，并通过构建航速与耗油和耗时的反向增减函数，对它们进行平衡制约[5]。再一方面，考虑到港口位置和距离受控制区覆盖程度的影响，合理组合港口间航段，安排航线挂港次序，确定航次航行路径，可有效降低航次的运营成本，提高航次的运营效率。因此，综合考虑以上各方决策内容之间存在的相互影响、相互作用、相互耦合，以及相关因素存在的效应悖反和相互平衡关系，选取船舶进出港射角、区内区外航段航速、航线挂港次序为决策变量，以航线挂靠港口确定下和满足航线货运需求的航次运营总成本最小为目标函数，构建一个排放控制区下集装箱班轮航线路径规划与航速调度的两阶段集成决策模型。

2 模型构建

2.1 条件假设

(1)模型中港口间距离实际为船舶海上最短航行距离；

(2)航线航次营运收益不受船舶挂港次序影响；

(3)船舶耗油量受燃油品质影响可忽略不计。

2.2 模型参数

对于一组给定挂靠港口，P表示港口集合，其中，K为航线挂港数量；G表示船舶在i,j港间航行过程的集合，E、A、N分别表示船舶驶离排放控制区、驶入排放控制区和控制区外的航行过程；C表示航次船舶运营成本；fo 表示燃油，chr 表示租金，表示船舶在i,j港间燃油费用，表示船舶租金费用。o、v用来区分不同位置，分别表示港口和港口距控制区外沿最近点，分别表示第i,j港坐标，表示i,j港坐标连线的斜率；、分别表示第i,j港距控制区外沿最近点坐标，分别表示i,j港坐标与距其控制区外沿最近点坐标连线的斜率；hi,hj分别表示第i,j港垂直于排放控制区外沿的距离；分别表示在i,j港间，船舶驶离i港控制区、驶入j港控制区以及控制区外的航行距离；q(E)、q(A)、q(N)分别表示船舶驶离控制区、驶入控制区和控制区外不同航速对应的日燃油消耗量；L表示港口间实际航行总距离；T表示航次时间；fMGO、fLSFO分别表示船舶在排放控制区内、外消耗的轻质柴油价格和低硫燃油价格；vmax、vmin分别表示船舶最大和最小航速；σ表示港口P集合的子集，σ∈P；f表示船舶发班频率；z表示发班间隔时间的余数；ki、kj、di、dj分别表示i,j港排放控制区边界外沿函数的系数和常数；αi、αj分别表示船舶出i港、进j港射角的最大值；βi、βj分别表示i,j港至船舶进出控制区外沿任意点形成直线与两港间“直线”航迹的夹角。

2.3 决策变量

图2 相关参数示意图Fig.2 Illustration of relevant parameters

2.4 模型构建

排放控制区下集装箱班轮航线路径规划与航速调度两阶段集成决策模型可构建如下：

阶段1 确定航线挂港次序

目标函数式(1)表示航次运营成本最小下的船舶最优挂港次序；式(2)表示船舶在i,j港间的燃油费用；式(3)表示i,j港间航行时间；式(4)～式(7)表示船舶驶离和驶入排放控制区外沿上的点坐标；式(8)和式(9)表示船舶在离港和入港控制区航行距离；式(10)表示船舶在排放控制区外航行距离；式(11)表示港口至船舶进出控制区外沿任意点形成直线与两港间“直线”航迹的夹角约束；式(12)和式(13)表示需要确定的船舶进出港射角的变化范围；式(14)表示船舶在i,j港间燃油费用约束；式(15)表示船舶在i,j港的航行时间约束；式(16)表示船舶在i,j港间航速的约束；式(17)表示船舶进离港航迹与排放控制区外沿的交点约束；式(18)和式(19)表示最优挂港次序约束；式(20)和式(21)表示0-1整数约束。

阶段2 确定发班间隔时间

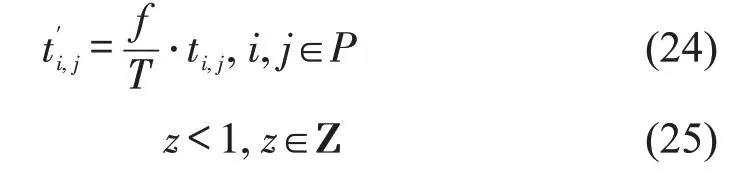
式(22)为目标函数，表示航次发班间隔时间优化值；式(23)表示航次总时间；式(24)表示船舶在i,j港间的优化航行时间，并返回阶段1 模型；式(25)表示发班间隔时间约束条件。

2.5 优化过程

模型优化过程如图3所示，具体步骤如下：

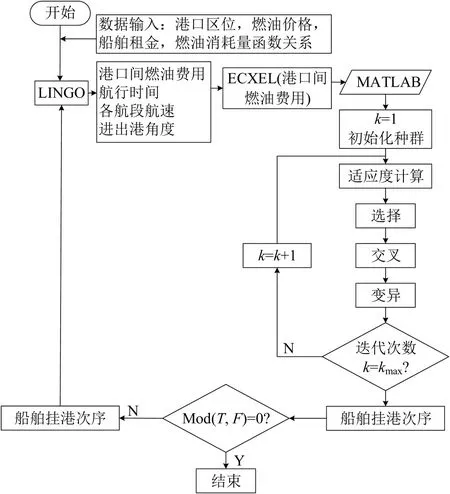
图3 优化过程Fig.3 Process of optimization

Step 1 将已知数据，挂靠港口位置坐标、港口距其控制区外沿最近点坐标、港口间距、船舶租金、燃油价格、燃油消耗量函数关系输入LINGO软件，应用阶段1模型，计算港口间燃油费用与对应航行时间。

Step 2 基于Step 1，将港口间燃油费用输入EXCEL，并导入MATLAB，利用遗传算法，经过适应度计算、选择、交叉、变异、达到迭代次数后终止，计算出阶段1 的航线挂港次序。其中，遗传算法采用港口编号对染色体编码，每个染色体表示一个港口挂靠顺序安排，染色体长度等于船舶挂靠港口数量。

Step 3 基于Step 2 获得的航线挂港次序，以及对应的航次运营时间，对航次运营时间与发班间隔时间进行取余，若余数符合条件，则导入Step 4，保留航线挂港次序；否则，通过LINGO 软件进行航次运营时间的整数化处理，获得阶段2中的船舶航次运营时间及各航段航行时间，并重复Step 1～Step 3。

Step 4 获得最优航线挂港次序。

3 案例分析

3.1 航线设定

现有某一集装箱班轮航线，挂靠港口为①、②、③、④、⑤、⑥港，其中①-④港已实施排放控制区，各港口和排放控制区分布如图4所示。航线配置船型为2000 TEU，租金10000 美元·d-1，最大航速为28 kn，最小航速为6 kn。船舶在①、②、③、④港作业时间分别为1 d，在⑤和⑥港各为0.5 d。

图4 各港口和排放控制区分布情况Fig.4 Distribution of ports and ECAs

对上述航线进行案例分析。首先，设计案例1 为船舶“直线”航行方式，即经济航速下航次成本最小化，获得航线港口挂靠次序与运营成本。然后，设计案例2 为船舶“折线”航行方式，即运用本文构建模型，获得航线挂靠港口次序与运营成本。在此基础上，对案例1 与案例2 结果进行对比分析，解析轻质柴油与低硫燃油价格变化情况，对决策变量船舶进出港射角、航段航速及挂港顺序的影响效果。

3.2 基础数据

有关该航线挂靠港口和该港口距其控制区外沿最近点的坐标，以及港口间实际最短航行距离分别如表1和表2所示。

表1 挂靠港口与港口距排放控制区外沿最近点坐标Table 1 Coordinates of calling ports and closest points from those to outer edge of ECAs

表2 挂靠港口间实际最短航行距离分布Table 2 Actual shortest voyage distances between calling ports(n mile)

针对该航线配置船型的船舶规范，采集该船不同航速下的燃油消耗量，利用回归分析法，获得航速与燃油消耗量的拟合函数关系为

选择排放控制区内外燃油价格为：轻质柴油700美元·t-1，低硫燃油320美元·t-1。

3.3 结果分析

根据优化过程步骤设计，运用EXCEL、LINGO与MATLAB 编程软件，使用本文构建的两阶段模型，优化案例1和案例2，结果如表3和表4所示，搜索过程如图5和图6所示。轻质柴油与低硫燃油的比值变化对船舶进出港射角、航段航速、挂港次序的影响分析，如图7、图8和表5所示。

表3 不同案例下航线挂港次序和相关费用Table 3 Port sequences and related costs under different cases

(1)不同案例下航线优化结果对比分析

表3 中案例1 的计算结果为：船舶在常规恒定经济航速下，即式(26)最小极值航速(13.5 kn)，在两港间采用“直线”航行，通过控制区消耗轻质柴油、非控制区消耗低硫燃油计算费用，获得航线最短距离挂港顺序为1→2→3→4→5→6，航次耗油费用为57.6×103美元。案例2 的计算结果为：应用本文提出的两阶段集成决策模型，船舶在两港间采用“折线”航行，通过控制区内外航速优化，获得航线最低费用挂港次序为1→3→2→4→5→6，航次耗油费用为51.6×103美元。对比案例1 与案例2 控制区内、外航行距离可知，案例2 之所以改变航线挂港次序，主要是由于案例2 控制区内航行距离比案例1减少了304.7 n mile，即使航行总距离比案例1增加了80.3 n mile，但是航次运营总费用减少了6000美元。图5 和图6 分别给出了案例1 和案例2 的优化求解搜索过程，由于航线挂靠港口数量规模较小，在迭代次数约5～6次便趋于最优，平均解也同步保持趋于稳定。

图5 案例1Fig.5 Case 1

图6 案例2Fig.6 Case 2

针对表3航次运营时间的非整数结果，运用本文构建的第2 阶段决策模型，对案例2 进行班期优化。采用表4 中缩时取整(10 d)，结果显示，控制区内航距略有增加，控制区外航距则相应减少，航次总航行距离整体减少；同时耗时费用略有降低，耗油费用稍有增加，航次总费用整体有所增加，挂港次序保持不变。反之，采用班期延时取整(11 d)，结果显示，控制区内航距略有减少，控制区外航距稍有增加，航次总航行距离整体增加；同时耗时费用略有增加，耗油费用稍有减少，航次总费用有所增加，挂港次序依旧不变。就本航线给出的案例而言，缩时优化结果优于延时优化结果。至于采用延时还是缩时进行班期优化，还需具体考虑船舶的市场租金和燃油价格影响。

表4 班期优化下的航线挂港次序和相关费用Table 4 Port sequences and related costs under optimization of sailing frequency

(2)燃油价格对进出港射角的影响分析

船舶进出排放控制区的射角，除了受挂靠港口区位和控制区域范围影响外，主要受轻质柴油与低硫燃油价格比值影响。如图7所示，轻质柴油与低硫燃油价格相差越小，船舶进出港射角越大，即控制区内航迹与控制区外航迹形成“折线”越不明显，当轻质柴油与低硫燃油价格相等时，射角最大，即两港间的所谓“直线”航行；轻质柴油与低硫燃油价格相差越大，船舶进出港射角越小，即控制区内航迹与控制区外航迹形成“折线”越明显，当轻质柴油与低硫燃油价格比值大到一定时，射角趋于0°，即船舶行驶需经过两港控制区外沿最近点，进行“折线”航行。

图7 燃油价格对船舶进出港角度的影响Fig.7 Influences on angle of port-entry and port-exit of fuel prices

(3)燃油价格对控制区内外航速的影响分析

控制区内外航速受航行距离、燃油价格、租金费用共同影响。图8表明：轻质柴油与低硫燃油价格相差越小，船舶在控制区内外航速差距越小，当轻质柴油与低硫燃油价格相等时，控制区内外航速相等；轻质柴油与低硫燃油价格相差越大，船舶在控制区内的航速相对越低，耗油费用相对越少，控制区外航速则相对越快，耗时费用相对越少，以此平衡船舶在港口间航行的整体费用。

图8 燃油价格对航速的影响Fig.8 Influences on navigation speeds of different fuel prices

(4)燃油价格对航线挂港次序的影响分析

排放控制区下航线挂港次序，不仅受航行距离影响，还受轻质柴油与低硫燃油价格比值影响。表5结果显示：当轻质柴油与低硫燃油价格差异较小时，控制区内耗油费用对挂港次序影响并不突出，航线挂港顺序为1→2→3→4→5→6，当轻质柴油与低硫燃油价格相等时，船舶在各港间“直线”航行，与航次最短距离的挂港顺序一致；当轻质柴油与低硫燃油价格差异逐渐增大，控制区内耗油费用的影响开始突出，当价格比达到在600/320时，航线挂港顺序发生改变，为1→3→2→4→5→6。

表5 燃油价格比对决策变量影响分析Table 5 Influence analysis on decision variables of different fuel price rates

4 结论

针对轻质柴油与低硫燃油的价格差异，对排放控制区下集装箱班轮航线运营成本带来的影响，本文构建了排放控制区下的集成决策模型。通过案例应用，对比结果表明，考虑船舶进出港射角、航段航速及挂港顺序优化的“折线”航行，要优于传统最短距离优化的“直线”航行。趋势分析表明，控制区内外燃油价格不同，船舶进出港射角则不同，控制区内外航行距离比例则不同，基于上述耦合关系，优化航段航速，平衡航次耗时费用与耗油费用，调整挂港次序，可有效降低航次运营成本，提高航线运营质量。可见，本文提出的排放控制区下集装箱班轮航线路径规划与航速调度集成决策问题具有一定理论研究价值，构建的两阶段决策模型能为集装箱班轮航线的设计提供决策参考。鉴于航次燃油补给在不同挂靠港的价格变化，未来可以研究排放控制区下燃油补给与航速优化协调调度问题。