城市轨道交通新建线路对沿线住宅价格增值的时空效应

张书婧，许奇，贾顺平，廖婧仪

(北京交通大学，a.综合交通运输大数据应用技术交通运输行业重点实验室；b.交通运输学院，北京100044)

0 引言

城市轨道交通在城镇化快速发展的中国内地具有极大的刚性需求，但同时也面临着建设资金短缺和运营入不敷出等难题。作为典型的公共产品，城市轨道交通具有正外部性突出的特点，集中体现在对沿线土地价值的增值(Land Value Uplift,LVU)效应，又称土地溢价。定量评估城市轨道交通的外部效益及时空差异，将有助于设置合理的土地溢价捕获模式反哺轨道交通建设和运营。

既有研究多采用特征价格模型(Hedonic Price Model,HPM)评估轨道交通的土地价值增值效应。基于最小二乘法回归(Ordinary Least Squares,OLS)的HPM 由于忽略变量之间的空间依赖性和异质性，对空间数据的解释能力较弱。随着空间分析技术成熟，部分学者引入全局常参数的空间计量模型[1]和局部变参数的地理加权回归模型(Geographically Weighted Regression,GWR)[2]进行研究。由于地理对象的时空模式是依尺度存在并由局部特征叠加的[3]，全局模型用于分析空间大尺度相关特征[4]，而局部模型关注小尺度下的细节特征，两者均不能独立刻画研究对象的全貌，因此需要综合考虑两种模型的特点对研究对象进行分析。

城市轨道交通对沿线土地价值的影响可分为空间效应和时间效应。在空间效应方面，多数研究围绕轨道交通邻近度与房地产价格的关系进行剖析，提出邻近轨道交通车站可以产生明显的LVU[5]。也有研究认为城市轨道交通对住宅价格具有负效应[6]或无明显影响[7]。近年来，越来越多的学者注意到城市轨道交通对房地产价格影响的空间异质性[8-9]，不同空间位置下轨道交通对房地产价格的影响差异成为空间效应研究的热点。在时间效应方面，大部分学者主要关注单条线路或单一站点在不同时段对周边土地价值的影响[10-11]，而对整个城市轨道交通线网的网络化效应及其LVU 的考虑不够充分。

关于轨道交通对土地价值影响的实证研究最初主要集中在北美地区[12]，其轨道交通制式与城市发展模式与国内大不相同。国内由于城市轨道交通发展与住房商品化起步较晚，对该问题关注相对较少，既有研究大多围绕北京、上海、武汉、杭州等城市的单一线路或小型轨道交通网络[13-14]。北京房地产市场发展成熟，其轨道交通线网规模为研究网络化效应对住宅价格的影响提供了必要条件。本文以北京市城市轨道交通整体线网为研究对象，综合利用HPM框架下的全局模型和局部模型分析新建轨道交通线路对土地价格增值的时空效应，可为今后的研究提供借鉴思路。

1 研究方法

1.1 特征价格模型

既有研究普遍采用HPM作为评估房地产价格的工具，其基本原理是将房地产作为异质性商品，差异来源于房地产本身所具有的可以满足消费者需求的某种特征的集合。该方法能够综合考虑各种影响房地产价格的特征，解释房地产商品的异质性。据此，本文采用HPM作为研究框架，房地产价格与各特征因素的关系可以表示为

式中：P为住宅价格；S、L、N、T分别为建筑特征变量、区位特征变量、邻里特征变量及交通特征变量的特征向量。

1.2 模型说明

多元线性回归(Multi-var iable Linear Regression,MLR)模型是HPM最基本的表达形式，通常用OLS进行参数估计，属于全局模型，公式为

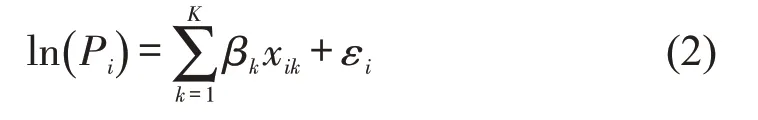
式中：Pi为第i份样本的平均单价，i=1,2,…N；xik为第i份样本的第k个特征变量，k=1,2,…K；βk为待估参数；εi为误差项。HPM通常有线性、对数和半对数等形式，本文采用HPM 的半对数形式进行分析，能有效处理异方差性问题。

由于MLR 模型假设各因素空间平稳，故对空间数据的解释能力有限，无法体现样本价格之间极强的空间自相关性。鉴于此，部分学者引入全局常参数的空间计量经济模型，包括空间滞后模型(Spatial Lag Model,SLM)、空间误差模型(Spatial Error Model,SEM)、空间杜宾模型(Spatial Durbin Model,SDM)等，其HPM形式分别为

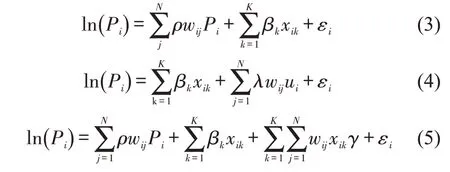
式中：wij为空间权重矩阵，由样本i和j的经纬度坐标确定，i,j=1,2,…N；ρ、λ分别为空间滞后项wijPi和空间误差项wijui的系数；γ为待估参数。

全局常参数的空间计量经济模型虽能较好地弥补MLR 模型的缺陷，但仍未能充分考虑空间异质性对房地产价格的影响，且不易在地图上可视化呈现。鉴于此，Du等[15]将GWR引入到交通领域的研究中。作为局部变参数回归模型，GWR 利用基于空间距离加权的局部样本估计每份样本的参数，能够较充分地考虑到房地产价格的空间异质性，在分析细粒度的空间关系时比全局模型更具优势。其HPM形式为

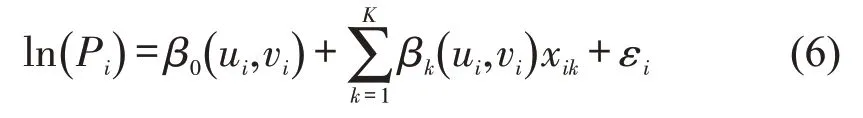
1.3 模型估计效果的评估

本文选取R2、Adjust-R2、对数似然值(Loglikelihood)、赤池信息量准则(Akaike Information Criterion,AIC)以及残差的莫兰指数(MoransI)，对MLR、SLM、SEM、SDM和GWR模型的拟合优度及对空间特征的考虑程度进行对比。R2、Adjust-R2、Log-likelihood越大，AIC越小，模型拟合效果越好。空间自相关程度用MoransI来衡量，其值在[-1,1]。MoransI大于0 表示空间正相关，反之表示空间负相关；越趋近于-1或1表明空间相关性越明显，反之表明不存在空间相关性。

2 研究案例与变量说明

2.1 研究范围及数据说明

本文以北京市轨道交通整体线网为研究对象，从链家网(lianjia.com)获取北京市二手房交易价格及相关属性信息。经数据预处理，共得到2011年1月—2016年3月期间6153个小区的361053个二手房交易样本。如图1所示，2011—2016年北京市城市轨道交通网络化发展较快，运营里程由336 km增加至554 km，中心城区线网逐渐加密并向郊区延伸。从二手房交易数据可知，住宅价格同样大幅上涨，2016年全市二手房平均交易价格相比2011年增长93%。2011—2016年北京市房地产调控政策总体变化平稳，为研究政策外的其他因素对住宅价格的影响提供了有利条件。

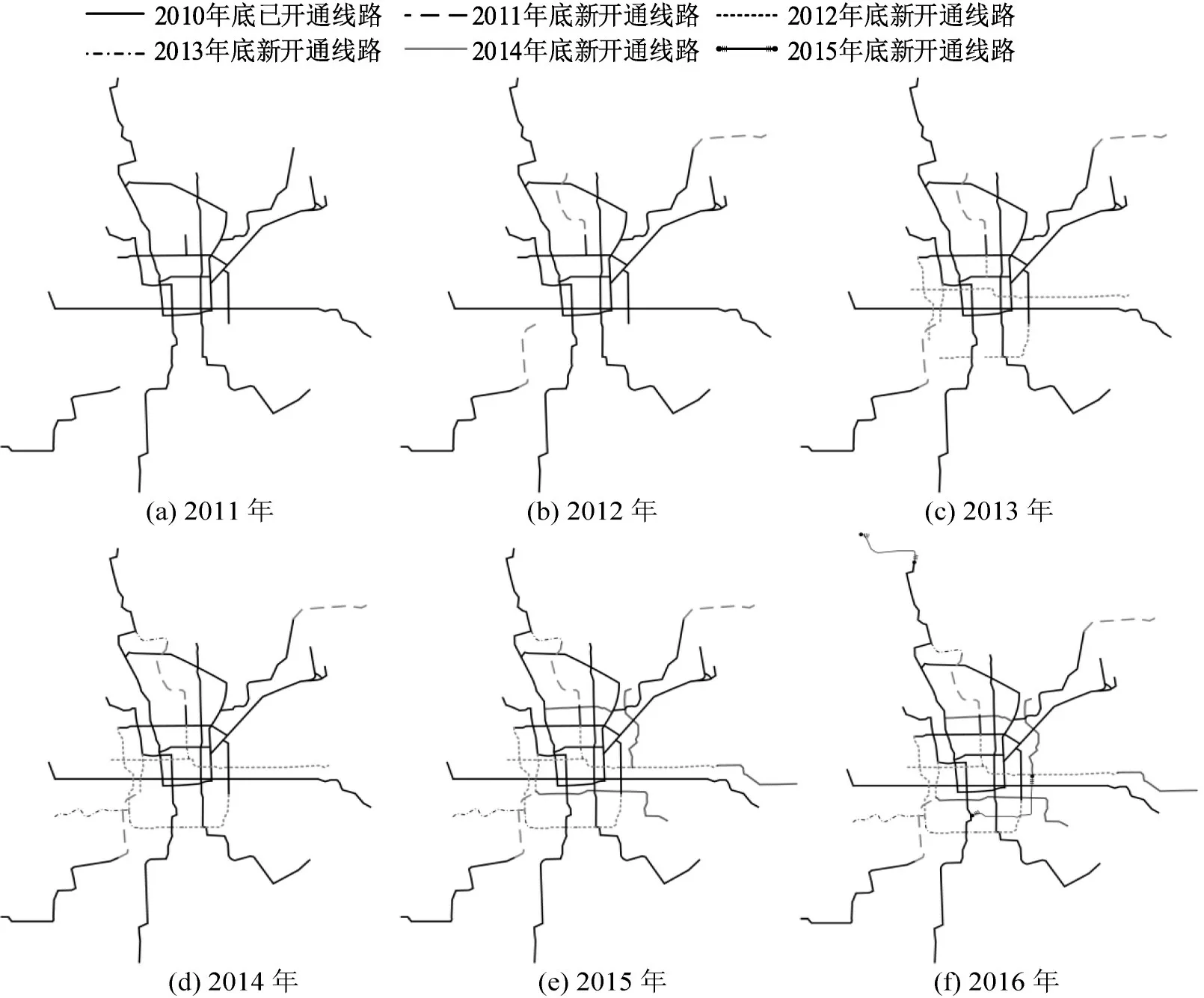
图1 2011—2016年北京市城市轨道交通线网图Fig.1 Development of urban rail transit network in Beijing from 2011 to 2016

2.2 模型变量选取

由于轨道交通对土地价值影响的粒度最小只能细化至住宅小区，而小区内每一个住宅的价格区别则取决于建筑特征属性；另外，样本量较大而数据处理能力有限，计算成本过高是在确定变量过程中不得不考虑的因素。因此本文对所得样本数据进行集计处理，将研究空间粒度确定为住宅小区。表1为模型变量的描述性统计，因变量为二手房交易价格，自变量为影响住宅价格的13 种属性特征。既有研究通常利用虚拟时间变量来考虑政策环境、市场变化等宏观因素的影响，本文主要分析新线开通前后对住宅价格的影响，使用2011—2016年截面数据，故未将虚拟时间变量纳入模型中。

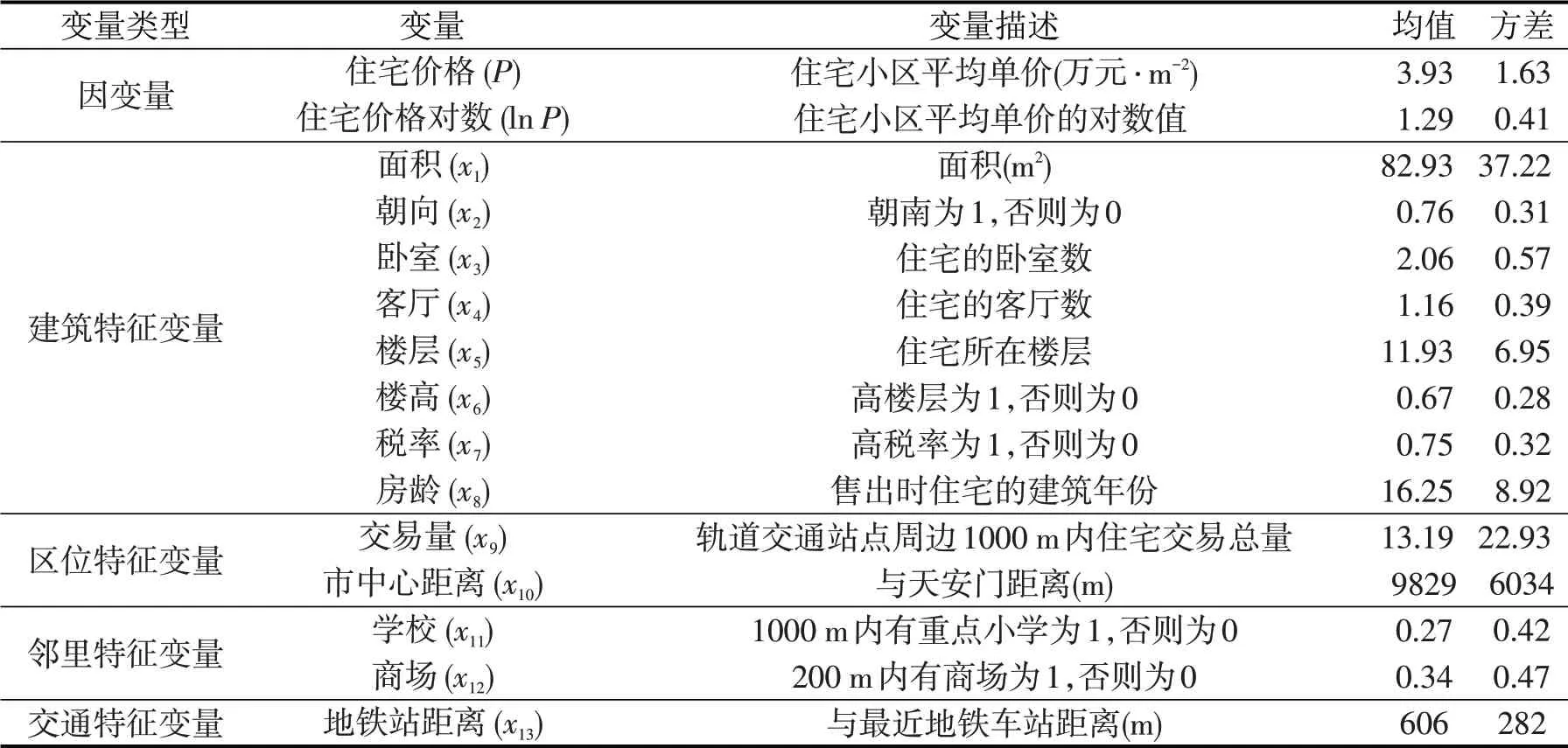
表1 模型变量的描述性统计Table 1 Descriptive statistics of variables in model

3 结果分析

3.1 参数估计结果

利用MATLAB空间计量工具箱对2011—2016年的截面数据进行拟合，表2为MLR与GWR模型的参数估计值及显著性水平。回归模型均采用半对数形式，估计系数β表示当住宅的第i个特征变量变化1个单位时的价格变化(100×βk)%。

表2 回归模型参数估计结果Table 2 Estimation results of regression models

从全局角度来看，地铁站距离(x13)在2011—2016年的显著性水平均处于10%以上，对住宅价格的影响较显著。然而，MLR 模型仅能得到各变量唯一的估计系数β，未能考虑不同地理位置住宅的属性特征对价格影响的差异，而GWR 模型则可以清晰地刻画空间异质性。在GWR 模型估计结果中，超过80%的样本在1%、5%或10%水平上显著，

β均值为负，说明对于多数样本，距地铁站越近，住宅价格会明显提升。x13的平均估计系数为-0.000063，意味着地铁站距离每增加1 km，住宅价格平均降低6.3%。同理，2012—2016年地铁站距离每增加1 km，住宅价格分别平均降低6.4%、5.8%、5.5%、6.7%、6.4%。此外，学校(x11)和商场(x12)、市中心距离(x10)与住宅价格在全局模型和局部模型中均显著相关，说明对于北京市二手房交易市场，区位和邻里特征很大程度上决定交易价格，郊区住宅价格总体小于市中心，学区房或周边商业设施完善的住宅价格总体更高。

表3 为5 种HPM 模型拟合效果的评价指标。与MLR、SLM、SEM、SDM 相比，GWR 模型所得R2(0.546～0.809)与Adjust-R2(0.543～0.809)更大，AIC值(-5958.95～-5117.48)更小，表明其拟合效果最为理想，对住宅价格具有更好的解释能力。同时，GWR 拟合后所得到的残差MoransI值(0.011～0.086)最小，能够更大程度降低残差的空间自相关。因此，无论在拟合效果还是空间效应处理能力方面GWR模型都明显优于全局模型。

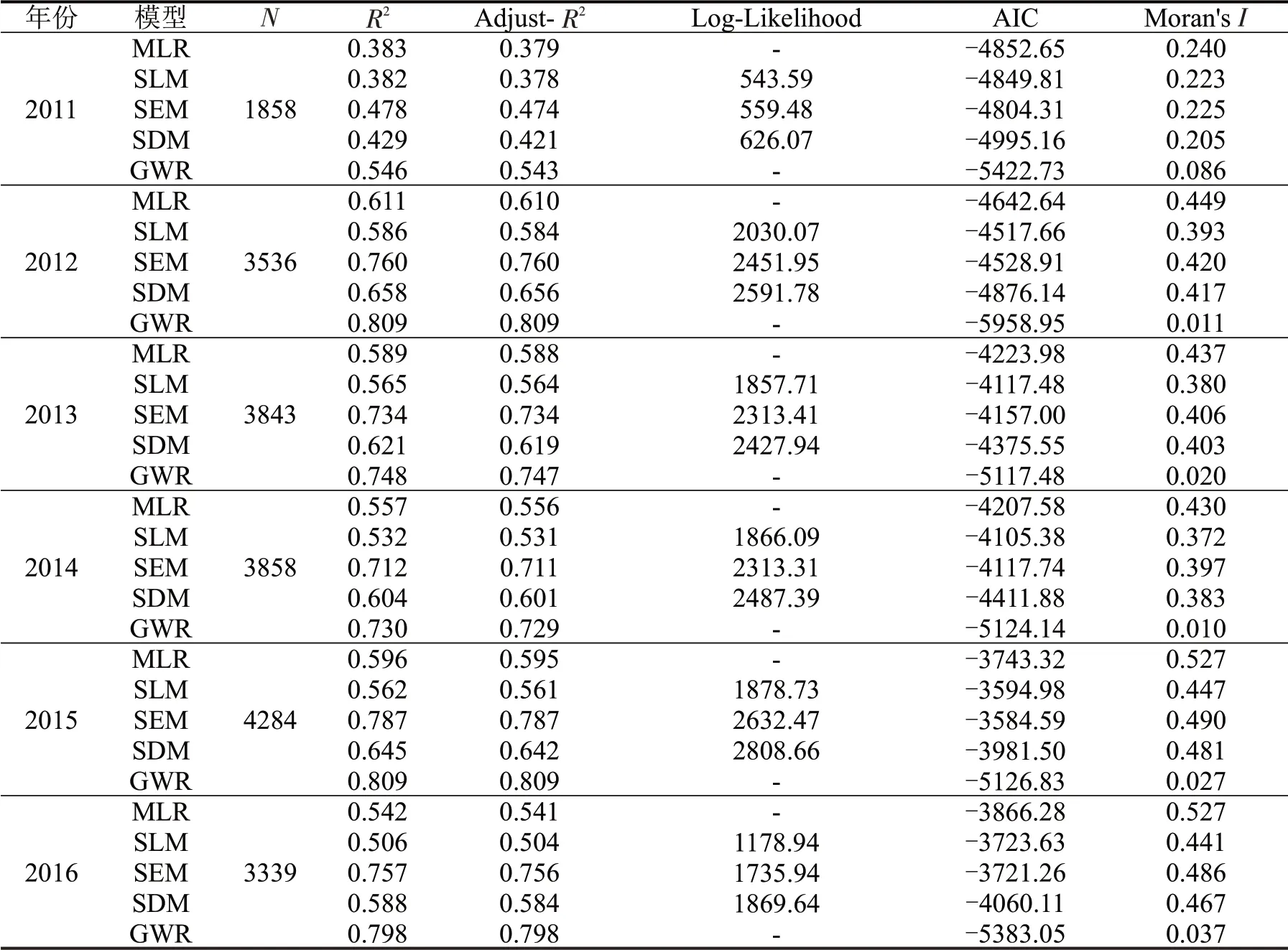
表3 回归模型拟合效果对比Table 3 Aggregate goodness of fit measures of regression models for estimation comparison

3.2 空间效应分析

地铁站距离(x13)的估计系数βt,m的空间分布情况如图2所示，t表示年份，m=1 表示地铁站距离相比前一年未发生变化的样本点，m=2 表示地铁站距离减小或新增的交易小区。βt,m的绝对值越大，样本点颜色越深；显著性越强，样本点半径越大。

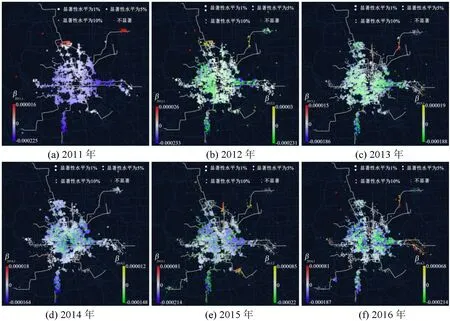
图2 2011—2016年地铁站距离(x13)估计系数的空间分布Fig.2 Spatial distribution of station distance(x13)estimated coefficient from 2011 to 2016

从市域范围来看，绝大多数二手房样本分布在北京五环内，五环外的样本主要集中在轨道交通沿线。城市轨道交通对住宅价格的影响在空间上不均衡，具有明显的区域差异。与既有研究不同的是，地铁站距离对住宅价格的影响程度并非完全随市中心距离递远递减，在五环内表现出显著且稳定的正效应，尤其在中关村、金融街、CBD、望京等大型科技园区或商务区，正效应更加显著。β值大于零且显著性较低的样本点大多集中于郊区线沿线和其与环线的换乘站周边，以及部分直径线或放射线在郊区临近终点站的位置。其中，大部分负效应产生的区域都在高架线、地面线附近，可能与此类线路造成的噪音污染及居住环境恶化有关。与既有研究差异的主要原因在于，北京呈多中心发展格局，随着首都功能的重新构建，众多产业功能向外疏解，核心区外分布有多个功能分区，轨道交通对住宅价格的影响在空间上的表现是各区位因素综合作用的结果。而既有研究中城市结构大多为老城区就业集中、交通发达，新城或卫星城相对落后，且轨道交通是连接郊区和市中心主要的交通方式，郊区住宅邻近轨道交通站点往往意味着更高的通勤效率，因此地铁站距离对郊区房价的增值作用更大。另外，既有研究大多只针对单条轨道交通线路进行讨论，对网络化效应的忽视也是造成该差异的原因之一。

城市轨道交通对住宅价格的影响具有明显的网络化效应。受新建线路直接影响的样本不仅β绝对值变化，其正负性也发生改变。如2011年15号线一期工程东段(后沙峪站至俸伯站)处于施工阶段时周边住宅β为正，2012年开通运营后变为负；昌八联络线施工期间周边房价受轨道交通负面影响，2013年新线开启空载试运行后变为正效应。新线开通也会改变整体线网对周边住宅价格的影响。随着线网加密，郊区与市中心的可达性不断提高，郊区线周边的新增交易小区逐年增加，轨道交通对郊区发展具有一定的拉动作用。相比市中心，郊区住宅价格受城市轨道交通新线开通影响的波动性更强。

这一发现为地方政府解决城市轨道交通建设的财政问题提供新思路，单一的税收制度并不适用于北京这样的特大型城市；相反，可以建立区域性的税收制度，或采用以香港“地铁+物业”为代表的联合发展模式，充分利用与沿线房地产项目的价值互动关系实现城市轨道交通的外部效益内部化。

3.3 时间效应分析

市场环境、政策、供需关系对房价变动具有至关重要的作用，但难以量化评估，其变化主要体现在时间因素中。图3 为地铁站1 km 范围内住宅在不同年份的价格增值(LVU)比率，1 km外住宅价格的变化几乎可以忽略。虽然地铁站距离和住宅价格总体呈现负相关，但也存在少量样本会受城市轨道交通的负面影响。2011年距地铁站1 km范围内的住宅价格受城市轨道交通影响平均产生2.79%的LVU，明显小于Ma[16]利用传统HPM计算得到的4.8%(800 m)。这与Kim[17]的观点吻合：若不修正空间自相关，HPM 估计得到的LVU 会被放大。2012—2016年，城市轨道交通产生的LVU 基本稳定，分别平均为2.88%、2.64%、2.41%、3.17%、3.05%；距离变化小区的平均正向价格增值比例分别为3.19%、2.82%、2.69%、3.58%、3.84%，略大于总样本的正向增值比例，表明新线开通对其直接影响范围内的小区房价具有相对更大的带动作用，但差异并不明显。

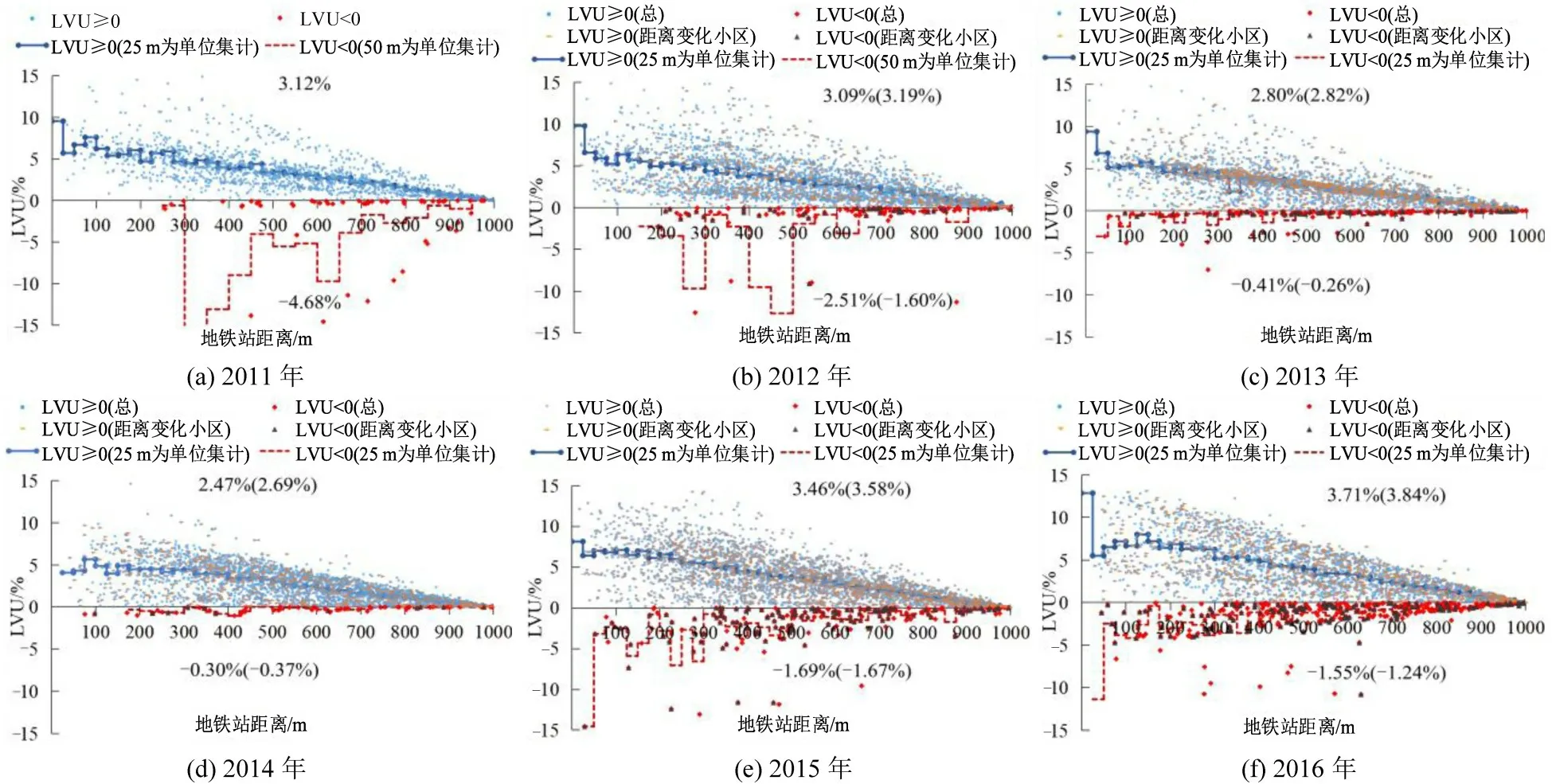
图3 2011—2016年车站1 km范围内住宅价格的增值比率Fig.3 Land value uplift within 1 km distance from metro station among 2011 to 2016

不同建设阶段城市轨道交通对土地价值增值的影响方面，本文分开通前和开通后两个阶段分析新线周边住宅价格增值比率的变化情况。以是否与地铁站距离减小为评判标准，选取分别于2012、2013、2014年开通的新线周边的3 组房地产样本，分析其在相应新线开通前1年和开通后3年内LVU的变化，如表4所示。第1组数据为受2012年新线开通影响与地铁站距离减小，且在之后3年内地铁站距离未发生变化的住宅小区，包括270 个样本；2011年为对应新线开通前的施工阶段，LVU 为3.26%，开通运营第1年LVU 提高至3.39%，运营第2年、第3年降至2.96%、1.97%。第2组数据样本量为43，在施工期间LVU 为2.51%，开通运营第1年LVU为2.76%，第2年为2.64%，2015年的LVU较大可能是由于数据量过小而造成的误差。第3 组数据由305 个住宅小区组成，在轨道交通施工期间LVU为2.25%，开通运营第1年提升至2.73%，运营第2年、第3年分别为2.70%、2.38%。可以发现，LVU在运营第1年比施工阶段产生一定提升，运营2年后会逐渐缓和；说明新线开通运营对房价有正向影响，但影响会随运营年份增加而减弱。

表4 受新线直接影响的住宅价格增值比率变化Table 4 Changes in land value uplift of residential properties directly affected by new line

4 结论

本文根据2011—2016年北京市二手房交易数据，采用HPM 框架下的全局常参数模型和局部变参数模型以及空间分析技术，定量评估北京城市轨道交通对住宅价格增值的时空效应。研究结果表明：

(1)与全局常参数模型的MLR、SLM、SEM 和SDM 相比，局部变参数的GWR 模型拟合所得R2与Adjust-R2最大，AIC值最小，在拟合优度及对变量的解释能力方面更具优势；其基本消除了残差的空间效应，更适用于分析城市轨道交通对土地价值影响的空间异质性。

(2)对于北京市二手房交易市场，市中心距离、学校、商场很大程度上决定住宅价格。全局模型与局部模型均表明地铁站距离对住宅价格具有显著的影响，影响范围约为1 km。

(3)在空间效应方面，LVU 总体随地铁站距递远递减，且表现出明显的空间异质性。轨道交通在五环内对住宅价格具有显著且稳定的正效应，增值效应不随与市中心(天安门)距离的增加而增加。城市轨道交通对住宅价格的影响在空间上具有网络化效应，新建线路不仅会改变周边房价，对城轨网络其他位置的住宅也具有影响。轨道交通线网的不断加密能够在一定程度上带动郊区发展。

(4)在时间效应方面，2011—2016年轨道交通对房价的影响基本稳定。轨道交通对住宅价格的影响在时间上同样具有网络化效应，新建线路对受其直接影响的小区房价具有相对更大的提升作用。新线开通运营对周边住宅价格有正面影响，但影响随运营年份增加而逐渐缓和。