传播动力学视角下集装箱海运网络关键港口节点识别

戈佳威，袁克镖，殷明，王学锋

(上海海事大学，交通运输学院，上海201306)

0 引言

固定航线、固定时间、固定港口是集装箱班轮运输的主要特征，受恶劣天气、运河堵塞、海事意外、罢工等众多不确定性因素影响[1-2]，港口拥堵事件屡见不鲜，“压港”现象造成船期延误，最终导致操作成本升高、准班率降低、船舶周转时间增加等多方面的不良影响。据统计，85%以上的船期延误是由港口因素导致[3]，并且，某一港口的延误会继续传播到下一港口，对整体集装箱海运网络的效率产生影响[4]。

针对延误问题，学术界从船期表设计、船期恢复、集装箱流恢复等多个角度进行研究，提出减少挂靠港、增加航班、提速航行等各种方案[3]，运用路径优化的方法，以成本或时间约束为目标建立数学模型，将延误影响范围控制到最小[5-6]。然而，鲜有研究从港口视角出发，对某一港口延误在整个海运网络中的进一步影响进行论证和阐述。

借助网络科学中的传播动力学理论，可以较好地识别延误在集装箱海运网络中的传播特性，并进一步识别重要的港口节点，进行针对性地维护(如在重点港口建设码头、提高装卸效率等)，避免船期延误扩散，有效地保障集装箱班轮运输的准班率。

1 世界集装箱海运网络SIS模拟

传播动力学理论源于对疾病传播特性的研究，通过SI、SIS、SIR及SIRS等传播模型进行预测和预防，其中，S(Susceptible)表示易染态、I(Infected)表示感染态、R(Recovered)表示恢复态。传播模型的建立一般基于3个假设，即总量不变、可感染性、可恢复性[7]。本文研究的世界集装箱海运网络满足上述假设：一是在本文研究区段内港口数量总体不变；二是由于集装箱班轮运输在挂靠时间和港口的选择上具有固定性，延误会“感染”下一港口，形成延误的“传播”，如疫情导致多国港口的拥堵，苏伊士运河拥堵蔓延至亚洲港口等；三是将港口延误视为“被感染”，经过一定时间，船期可以恢复到“正常状态”。此外，面对恶劣天气等“感染源”，港口对其没有“免疫功能”，会再次受到“感染”。根据传播动力学模型的特点，相比SI、SIR、SIRS 模型，港口延误问题适用于SIS模型求解，考虑到集装箱海运网络结构特征，改进SIS模型为

式中：St+It=1；St为t时刻处于易染态的节点数量(百分比)；ΔSt+1为从t时刻到t+1 时刻增加的易染态节点数量；It为t时刻处于感染态的节点数量(百分比)；ΔIt+1为从t时刻到t+1 时刻增加的感染态节点数量；β为传播速度；γ为感染后恢复速度；θ为度值为k′的某节点与度值为k节点相连的概率，为网络中度值为k′的节点密度；βk′(t)为t时刻度值为k′的节点被感染的概率；N为网络节点数量。

与此同时，世界集装箱海运网络具有无标度和小世界特性，其临界值满足无标度网络的传播阈值，k为港口度值。本文运用德鲁里数据库中2018年度世界主要航运企业的航线统计数据(296个港口，5059条连线)，计算世界集装箱海运网络的结构参数如表1所示，得到传播阈值为0.44。

表1 世界集装箱海运网络结构参数Table 1 Network parameters of world container shipping network

为度量各个港口节点的传播影响力，分别以每个港口作为初始影响(感染)源，在世界集装箱海运网络中模拟SIS 传播过程，通过t时刻感染节点的数量均值来表示港口节点的传播情况，即每个港口节点的影响规模。取传播速度为0.1，恢复速度为0.05，则传播效率ξ为2，满足传播阈值条件[7]。仿真时间为50步长，通过1000次重复试验，可得其传播影响力的数学期望排序，从排名前10的SIS模拟来看，该仿真结果符合业内对重要港口的一般认知[8]。新加坡传播能力为208；釜山、阿尔赫西拉斯、科隆、上海等度值排名前10的港口传播能力在200左右，超过85%的港口节点会被影响。

通过SIS 模拟发现，度值与传播能力相关性较强。度值越大，完成传播并达到最终规模的时间越短。图1为各时间步内感染节点数量的变化率，新加坡为初始感染节点时，受感染港口数增长速率最快，在t=6 时最先达到峰值，而后急剧降低，为排名前十港口中变化速率最快的港口。进一步引入排名第5、15 和20 的巴生、勒阿弗尔和杰贝阿里进行比较，发现随着度值的减少，传播能力出现减弱。另一方面，度值越小的港口，其受感染节点减少速度更为缓慢，以新加坡港和比雷埃夫斯港为例，传播爆发阶段，新加坡的感染速度远高于比雷埃夫斯，达到峰值后，变化率低于比雷埃夫斯港，后逐步趋于稳定。

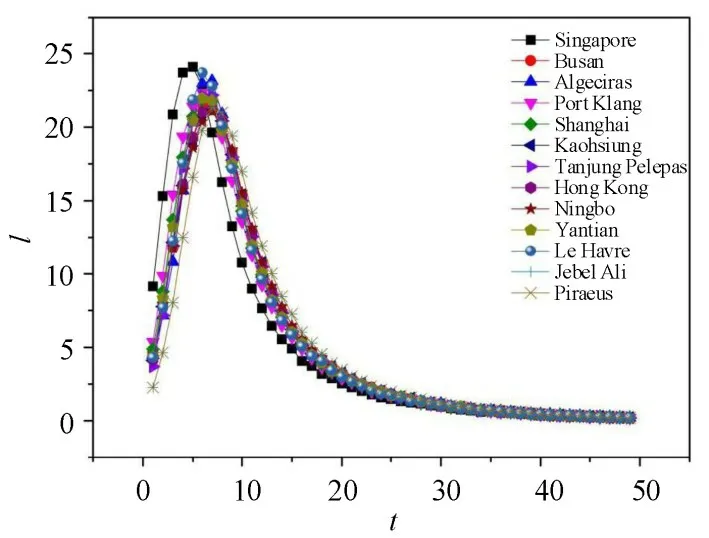
图1 不同港口为初始感染节点情况下被感染节点数量变化率Fig.1 Change rate of infected nodes with different initial infected ports

经函数拟合比较，港口传播能力与度值符合幂为16.84 的幂律分布。如图2所示，拟合优度r2=0.89，少数港口的传播能力大于大部分港口(度值小于16)，总体上传播能力随度值增加，但无明显特征标度。

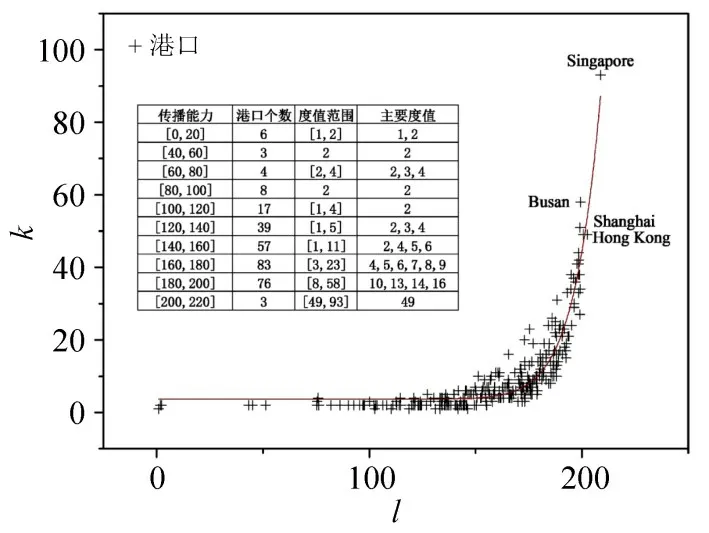
图2 传播能力与港口度值关系Fig.2 Relationship between spreading ability and port degree

根据平均场理论，对度值在16 以下且满足传播阈值假设条件的港口节点传播情况进行敏感性分析发现，随着传播速度的增加，曲线间的间距变小，最终传播范围逐步增大。图3为不同度值及传播速度，当β≤0.35 时呈显著变化，时变化微弱，β≥0.75 时并不明显。因此，不同度值港口为初始节点的传播影响力与传播速度正相关，且在传播速度较小时区分度更高。

图3 不同传播速度下不同度值港口为初始节点的传播情况Fig.3 Time series of infected ports under ports with different degree and infected rate

2 节点传播能力评估模型

近年来，随着人们对网络结构的进一步认识，结合网络结构探讨传播动力学行为的研究更为深入。影响节点传播能力的因素除了度值外，节点在网络中的地位、节点间的距离等同样是重要的影响因素[9]。为进一步刻画节点重要性，得到更为精确的影响力指标排序，通过度值、距离、重力公式等进一步细分，演化出几类改进模型。

(1)θ模型

基于k-壳层次分解法的理念，由于最大k-核对节点重要性和传播效率有一定影响，核数相同的两节点具有不同的连接对象和影响力，仅仅依靠k-壳分解法判断重要节点存在一定缺陷[10]。因此，通过联立最短路径长度、网络最大ks值(位于k-壳的节点度值)和节点所处位置，可以更好地识别重要节点的传播性能。

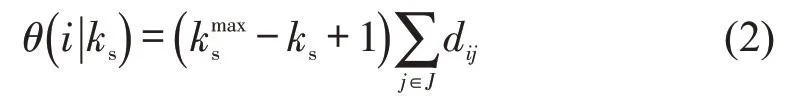
(2)k-壳混合模型(简称ksh)

同时，也可能存在外层节点的重要性比核心层高的情况[11]。通过最短联系距离、度值、两点间的k-壳值建立联合方程，即k-壳混合模型识别重要节点。

受计算复杂度影响，要计算所有节点间的距离十分耗时，为简化计算程序，对dij作出限制，当最短路径长度大于3 时停止，即考虑i节点周边3 个步长的邻居。

(3)引力模型

由于节点间的影响随着距离的变化逐步减弱，可通过引力模型[12]，建立邻居核心性重力公式，比较每一个层级内部的节点重要性。

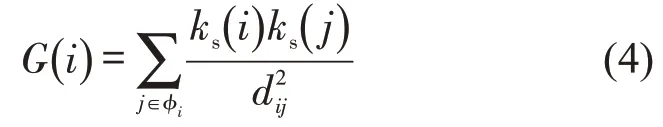
同样，为降低计算复杂度，本文仅考虑i节点周边3层(步长)的邻居。

上述模型各有侧重，尽管其有效性在众多社会网络中得到验证，但鲜有在世界集装箱海运网络上实现验证。

(4)改进的引力模型(简称ksw)

综合上述模型，本文提出改进引力模型进行精确划分，用度值、k-壳及节点间的最短路径长度来表示，主要变化在于：用节点度值与节点所在壳代替单一的节点壳数；利用权重设置综合取值方法，得到节点的综合值，；考虑邻居节点的综合取值。具体公式为

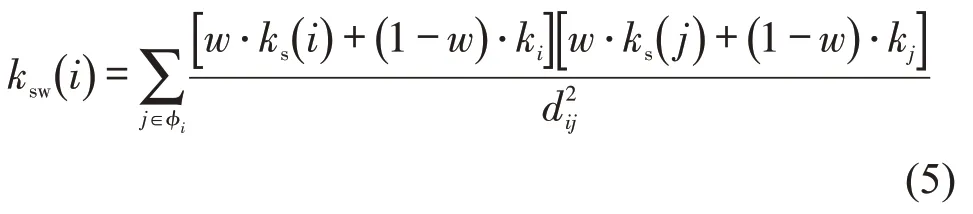
为验证改进的引力模型，并比较各个模型在衡量节点传播能力上的水平，即与SIS模型结果的差异，运用τ系数进行描述，设X为根据SIS 模型得出的节点传播能力排序，Y为其他模型得出的节点影响力排序，由此可得到一串对应的数组，，对于任意的i和j，如果xi ＞xj(或xi＜xj)，且yi ＞yj(或yi＜yj)，那么称这一对数组为一致的，反之则称其为不一致。进而定义

式中：nc为满足一致性的数组数量；nd为不一致的数组数量；n为数组总数。

由式(6)可知：τ越大，两个排序越接近；当τ=1时，说明两列数据完全相同，反映模型对节点的排序更符合网络传播的情况，从而证明该模型在传播动力学方面的精确度较其他模型更高。

3 模型检验及分析

本文选取度中心性、中介中心性、接近度中心性、特征向量中心性、k-壳分解法、θ法、ksh以及引力模型得到的节点传播能力排序，与通过SIS模型仿真运算得到的节点传播能力排序(传播速度为0.01，恢复速度为0.05，传播效率大于世界集装箱海运网络阈值，取1000次平均，时长为50)进行比较。

如表2所示，传统的中心性排序方法中，度中心性和中介中心性的相关度较高，在传播能力排序中依然有效，可见传播能力是基于节点的邻居节点数量和全局可达性，即港口的航线覆盖程度。而与邻接节点(港口)的重要性(由中介中心性和特征向量中心性反映)无关或负相关。

表2 各中心性方法排序与SIS传播模型排序比较Table 2 Comparison of centrality models and SIS ranking

改进的引力模型τ值达到0.222，较其他中心性方法和模型更优，适用性最强，其次为引力模型、θ和ksh法。k-壳分解法的τ值为负，可见其并不适用于评估世界集装箱海运网络的节点传播能力。通过引力模型、θ和ksh法的比较发现，节点间最短路径长度是衡量节点传播能力的一个重要因素。

进一步选取度中心性(DC)、中介中心性(BC)、引力模型(G)、ksh、θ、以及改进的引力模型与SIS传播模型的排序做比较，通过变换传播速度(β值)，可以看出，各个模型排序与SIS 模型排序的差异演化过程，如图4所示。当β=0.35 时，τ达到最高值，即所有模型与SIS排序差异均为最小，其中，ksw 的τ值为0.9755，节点传播能力基本与SIS 模型相同。

图4 不同传播速度下各评估模型τ 值变化Fig.4 τ value of evaluation models under different spreading speed

图5为各个模型排序的箱型图，可以发现，ksw模型τ的数学期望最高，其次为ksh、θ、引力模型、中介中心性和度中心性方法。在节点传播能力评估时，ksw 模型更为有效，进一步验证了其在世界集装箱海运网络节点传播能力评估中的适用性。

为进一步维护人民的生命安全与饮食健康，2009年2月28日，第十一届全国人民代表大会常务委员会第七次会议通过并发布了《中华人民共和国食品安全法》，同年6月1日起施行。直至2013年，实施4年的《中华人民共和国食品安全法》启动修订。随后，最新版的《中华人民共和国食品安全法》由中华人民共和国第十二届全国人民代表大会常务委员会第十四次会议于2015年4月24日修订通过，共十章，共计154条，并于同年10月1日起施行。

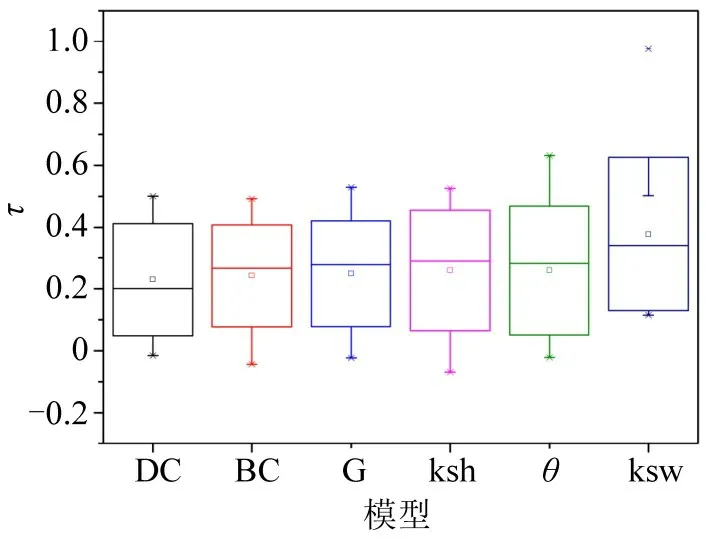
图5 各评估模型τ 检验箱型图Fig.5 Box diagram of evaluation models(τ test)

表3 根据各个模型列举了排名前20 的港口节点，在所有模型中，新加坡港均位列第一，说明其传播影响力最大并十分稳定；上海、釜山、阿尔赫西拉斯等港口紧随其后，始终保持在前十位，应依次保障各港口的正常挂靠。从改进的引力模型看，前十大港口中，亚洲港口占9 个，可见亚洲港口在世界范围内具有高影响力，其次为勒阿弗尔和鹿特丹等欧洲港口。由于各个模型的侧重点不同，某些港口的排名出现较大幅度变化，以阿尔赫西拉斯为例，具有相当高的度值和中介中心性，当考虑其所在壳时(k-壳分解)，其排名下滑至8～18位(ksh、θ和引力模型)，仅仅作为连通性港口，并没有作为始发港、目的港或中转港，并不会显著影响货物的运输，这一点从吞吐量可以得到证实，2018年全年集装箱吞吐量为477 万标箱。此外，从地理位置上看，其位于地中海直布罗陀海峡的咽喉，是亚欧海上运输的必经之地，像这样具有高连通性的港口，其传播影响力并不如度值更小(经过航线少)的上海港和巴生港，在选择放弃挂靠或增加在港作业效率(码头成本增加)时，应优先放弃阿尔赫西拉斯或优先保障上海港和巴生港的作业效率。

表3 各模型港口传播影响力排序(前20)Table 3 Ranking of port spreading ability(Top 20)

4 结论

本文通过传播动力学的视角，研究了延误在世界集装箱海运网络中的传播过程和特性，提出港口重要性排序的新方法。主要结论如下：

度值与传播能力相关性较强。港口节点传播能力与度值满足幂为16.84 的幂律分布，体现出无标度特征，少数港口的传播能力大于大部分港口。度值越大，完成传播并达到最终规模的时间越短。通过SIS 模拟及敏感性分析，高度值港口为初始感染节点的受感染港口数增长速率最快，而不同度值港口为初始节点的传播影响力与传播速度正相关。

提出并验证了改进的引力模型。除度值外，节点间最短路径的引入，对模型的精度提升有促进作用。基于综合取值法，，提出改进的引力模型。各模型的τ值计算表明，改进的引力模型在世界集装箱海运网络中的适用性更强，精确度更高。

模型的实证研究发现：①按照传播影响力对世界港口进行重新排序，以世界排名前二十的港口识别为例，保障正常挂靠和港口作业的顺序为新加坡、釜山、上海、巴生、阿尔赫西拉斯等港口。②高传播影响力港口普遍集中在亚洲区域，其次为欧洲地区；在各模型中，新加坡港、上海、巴生等港口影响力较高并保持稳定；阿尔赫西拉斯、鹿特丹、安特卫普等传统欧洲大港排名浮动较大，相较第一梯队的亚洲港口，影响力不强。③高连通性与高传播影响力无正相关性。上海港和阿尔赫西拉斯港的对比显示，在选择放弃挂靠或增加在港作业效率(码头成本增加)时，应优先放弃阿尔赫西拉斯港或优先保障上海港作业效率。

未来还可在不同情境下进一步论证模型的适用性和有效性，通过特定事件、特定延误时间、特定挂靠港口等参数的设置，完善和丰富传播动力学理论在世界集装箱海运网络中的应用，为具体决策提供理论方案。