基于改进核密度估计的电动出租车快速充电行为研究

田晟，曾莉莉

(华南理工大学，土木与交通学院，广州510640)

0 引言

根据国务院办公厅正式发布的《新能源汽车产业发展规划(2020—2035)》，纯电动出租车等公共用车领域到2035年将全面实现电动化。通过统计学建模方法得到充电行为特征变量的概率分布模型，进而基于蒙特卡罗模拟实现充电负荷预测的研究较为广泛[1]，因此研究电动出租车充电行为规律是解决电动出租车规模化发展过程中面临的充电负荷准确预测、充电设施合理布局等问题的基础。

电动出租车是电动汽车的一种类型，电动汽车充电行为规律的研究数据来源经历了问卷调查数据、居民出行调查数据、传统燃油车辆实测数据到电动汽车实测数据。随着大数据和深度学习技术的发展，目前基于数据驱动的电动汽车充电行为研究已经成为热点[2]，主要有基于非监督学习方法进行电动汽车充电行为特征变量的预测和分析，如Chung 等[3]使用由支持向量机、随机森林和核密度估计组成的集成模型对充电持续时间、充电能量消耗的预测；基于监督学习方法进行电动汽车充电行为的聚类分析，如Shen等[4]使用K均值聚类算法将充电行为分为3类；基于深度学习模型进行充电负荷预测研究，如Zhu等[5]使用RNN模型预测公用充电站的逐时充电负荷。

目前充电行为特征变量的概率建模主要基于传统参数估计模型，然而该方法需要提前假设服从某种分布，然后依据历史样本数据估计该分布的参数，如果假设的概率分布与实际情况不符合，就会导致计算偏差较大。核密度估计(Kernel Density Estimation,KDE)是一种非参数估计方法，无需事先对随机变量的概率分布模型进行参数设定，能够真实体现数据本身的分布特点从而提高准确度[6]。非参数核密度估计模型已经广泛应用于集装箱集疏港时间的概率分布建模、交通荷载参数的统计分析和城市空气质量时空分布特征探究等多个领域，但将非参数核密度估计模型用于电动汽车充电行为特征变量概率建模的研究还较少。Wang 等[7]使用高斯核密度估计器确定充电行为特征变量的参数，但带宽限制了预测精度；Chen 等[8]将高斯核密度估计用于充电行为的分类；Chung 等[9]构建了由高斯核密度估计器和扩散核密度估计器组成的混合核密度估计器预测电动汽车的停留时间和充电需求，并且表明两类核密度估计器具有各自的优点。针对常规核密度估计存在边界误差、局部适应性低、峰谷扁平化等缺陷，缪鹏彬等[9]将具有边界核的自适应核密度估计模型应用到电动公共客车起始SOC 和起始充电时间的概率建模，有效解决了边界偏差和局部适应性低的问题；Nosratabadi等[12]提出的自适应核密度估计算法有效改善了局部适应性低的缺点。

考虑到传统参数估计模型和常规核密度估计模型拟合精度低的缺陷，本文提出一种基于扩散方程的自适应扩散核密度估计模型(Adaptive Diffusion Kernel Density Estimation,ADKDE)，采用渐进积分均方误差(Asymptotic Mean Integrated Squared Error,AMISE)获得最优带宽，最后将该模型应用于上海市电动出租车快速充电行为特征变量的概率分布建模，验证了本模型的可行性和准确性。

1 数据准备与分析

本文数据来源于新能源汽车国家大数据联盟平台，采集了上海市50 辆电动出租车的实际运行数据和充电数据，原始数据集包含3812555 个样本。数据的采集时间为2018年7月1日-7月30日，采集的时间间隔为10 s，数据集包括车辆编号、数据采集时间、充电状态、车辆型号、车速、累计行驶里程、电池荷电状态、总电压、总电流、经度、纬度等11个字段，基本情况如表1所示。

表1 上海电动出租车的实测数据Table 1 Measured data of Shanghai electric taxi

1.1 充电片段划分与结果

原始数据因采集过程中受到干扰而存在噪音数据，因此先使用Python对原始数据集进行数据清洗和数据预处理，然后进行片段划分，区分放电数据(车辆正在行驶时产生的数据)和充电数据(车辆停车充电时产生的数据)。制定充电片段的划分依据如下：

(1)判断车辆充电状态c_stat 是否等于3 并且车辆速度speed 是否等于0，若满足条件则保存，经过该操作得到所有充电数据；

(2)依次按车辆编号vid、数据采集时间Daq_time进行升序排列，再根据车辆编号不同切分所有充电数据，经过该操作得到50 辆电动出租车各自的充电数据；

(3)针对每一辆电动出租车的充电数据，判断电池荷电状态soc是否连续增加，若是连续增加，则将这一个片段截取下来单独保存至csv 文件，重复这一操作，直至所有充电数据被分割完成，即可得到所有的充电片段。

按照上述流程对原始数据集进行操作，共得到558745条充电数据和1290个充电片段。然后在已经划分好的充电片段中删除soc 无变化的片段，最终得到有效充电片段1201个。本文研究对象是电动出租车的快速充电行为，因此还需要制定条件从得到的有效充电片段中筛选出快速充电片段。根据充电时电压在[300,400]V，电流在[100，200]A这一条件，从所有的有效充电片段中筛选出快速充电片段，共得到1074个快速充电片段，电动出租车充电片段分析如表2所示。

从表2可以得出：上海市电动出租车用户更倾向于选择快速充电方式，所有充电片段中，快充比例为89.44%，慢充比例为10.56%；电动出租车用户在工作日期间选择快速充电的比例远远高于慢速充电的比例，双休日期间选择快速充电和慢速充电的比例差别较小。

表2 电动出租车充电片段分析Table 2 Charging segment analysis of electric taxi

1.2 快速充电行为特征变量的相关性分析

电动汽车的充电行为通常发生在用户某一次出行过程当中或者一次出行结束之后，电动汽车的充电行为特征变量包含3 个维度：充电电量，如开始充电SOC、结束充电SOC、已充电量；充电时间，如开始充电时刻、结束充电时刻、充电持续时间；充电方式，如快充、慢充等。根据1.1节得到的快速充电片段，从中提取充电起始SOC(SOC_start)、充电结束SOC(SOC_end)、充电前后SOC 变化量(SOC_increase)、充电起始时刻(charge_start)和充电持续时间(charge_duration)这5 个快速充电行为特征变量，为了揭示这5 个特征变量之间的相关关系，开展相关性分析，得到快速充电行为特征变量相关性热力图，如图1所示，快速充电行为特征变量的散点图如图2所示。

图1 快速充电行为特征变量相关性热力图Fig.1 Correlation thermodynamic diagram of characteristic variables of fast charging behavior

从图1 和图2 可以看出，快速充电行为特征变量之间存在相关性，为深入研究这两对特征变量之间的相关性程度，采用皮尔逊相关系数(Pearson Correlation Coefficient)和肯德尔秩相关系数(Kendall Rank Correlation Coefficient)进行描述，具体表现为充电持续时间和充电前后SOC 变化量存在正相关关系，皮尔逊相关系数达到0.641；充电起始SOC 和充电前后SOC 变化量之间存在显著的负相关关系，因为皮尔逊相关系数的值达到了-0.828，肯德尔秩相关系数的值达到了-0.773。

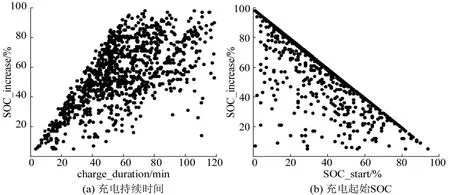
图2 快速充电行为特征变量散点图Fig.2 Scatter diagram of characteristic variables of fast charging behavior

2 基于改进核密度估计的快速充电行为特征变量概率建模

2.1 常规核密度估计模型

假设x1,x2,…,xn为电动出租车快速充电行为某一特征变量的n个样本，该特征变量的真实概率密度函数为f(x)，通过常规核密度估计方法得到的概率密度函数为

式中：x1,x2,…,xn为电动出租车充电行为某个特征变量的实测数据且存在取值范围，例如充电起始时刻的取值范围是[0,23]，xi为特征变量的第i个样本；n为样本总量；h为带宽；K()· 为核函数；Kh为带宽h的核函数。

基于常规核密度估计模型，当带宽固定时采用不同核函数，以及当核函数固定时采用不同带宽对充电起始时刻进行概率分布建模，得到核密度估计结果分别如图3和图4所示。

从图3 和图4 可以看出，快速充电起始时刻的数据样本分布存在多峰、不对称现象。当带宽h固定，分别采用三角核函数(Triangle)、高斯核函数(Gaussian)和依潘涅契科夫核函数(Epanechnikov)对充电起始时刻进行核密度估计时，不同核函数对于估计结果的影响非常小；当核函数固定，分别采用不同带宽对充电起始时刻进行核密度估计时，带宽对于估计结果造成的影响非常显著。因此，在非参数核密度估计中，带宽的选取非常重要。同时发现，高斯核函数在能够反映样本分布特征的同时具有良好的光滑度和可微性，故本文选取高斯核函数进行非参数核密度估计，基于高斯核函数的核密度估计公式为

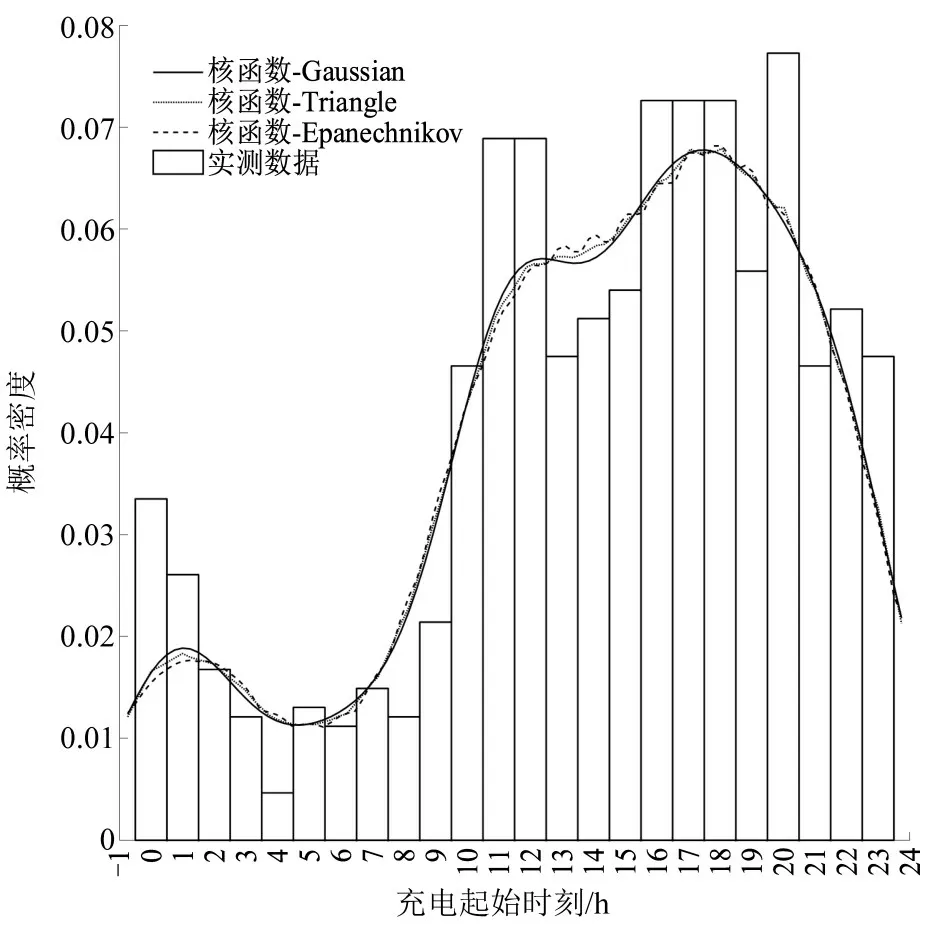
图3 采用不同核函数的核密度估计对比Fig.3 Comparison of kernel density estimation with different kernel functions

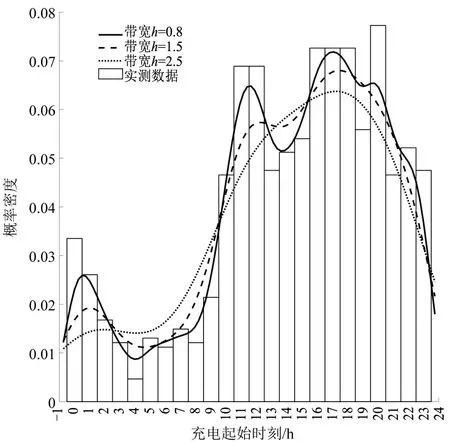
图4 采用不同带宽的核密度估计对比Fig.4 Comparison of kernel density estimation with different bandwidths

此外，通过快速充电起始时刻的样本数据分布情况可以看出，电动出租车充电行为特征变量的样本数据具有不确定性与波动性，表现为整体数据密度不均匀。如果使用常规核密度估计模型，整体最优带宽不能根据充电行为特征变量数据样本密度进行调整，导致其局部适应性较差。为解决这一问题，本文提出一种基于扩散方程的自适应扩散核密度估计模型，通过对传统的高斯核密度估计方法进行改进，提高其局部适应性。

2.2 自适应扩散核密度估计模型

热传导方程不仅仅描述热传导现象，也可以刻画分子、气体的扩散，因此也被称为扩散方程。利用Fourier 热力学定律和能量守恒定律得到一维傅里叶热传导方程为

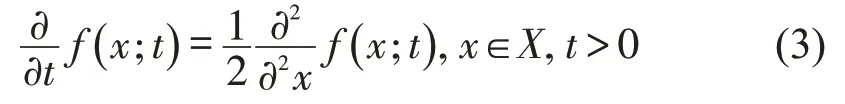
式中：X为特征变量x的样本集合。

Chaudhuri 等[12]在研究尺度空间理论时建立了热扩散过程和常规核密度估计的联系，证明了高斯核密度估计是傅里叶热方程的唯一解，并且t=h2，这意味着热扩散过程中的时间参数和核密度估计中带宽参数的平方具有相同的性能。式(3)的初始条件为

式中：Δx为式(3)的初始条件；为变量x的狄拉克测度。

选取具有自适应平滑性能的线性扩散过程对傅里叶热方程进行拓展，得到扩散核密度估计方程，线性扩散偏微分方程为

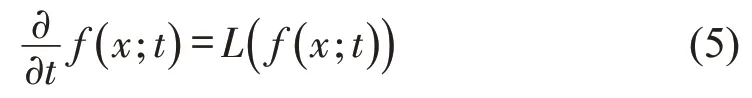
为了保证扩散偏微分方程取得唯一解，给定自适应扩散核密度估计的初始条件如式(4)所示，纽曼边界条件为

基于上述条件，对式(5)求解，得到自适应扩散核密度估计及其核函数表达式为

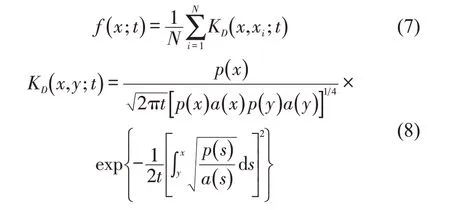
式中：KD()· 为扩散核函数；y为核函数定义域内的随机变量且y＜x；s为区间[ ]y,x之间的随机变量。为使扩散核密度估计取得唯一解，x,y需要满足

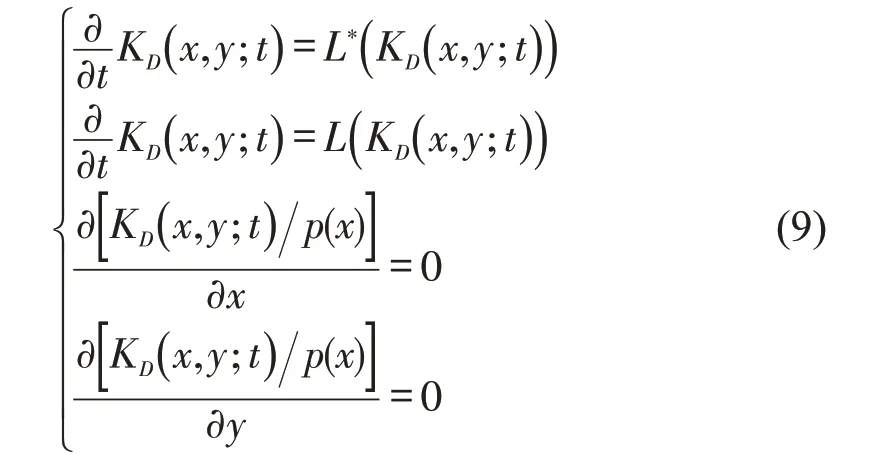
2.3 最优带宽的求解

根据核密度估计理论，通常采用平均积分平方误差(Mean Integrated Squared Error，MISE)衡量核密度估计值的全局准确度，MISE 的计算公式为

对式(10)进行泰勒展开并略去高阶项可以得到渐进积分均方误差。本文采用渐进积分均方误差求解提出的自适应扩散核密度估计模型的最优带宽[14]，求解该方法的渐进积分均方误差AMISE 可以表示为

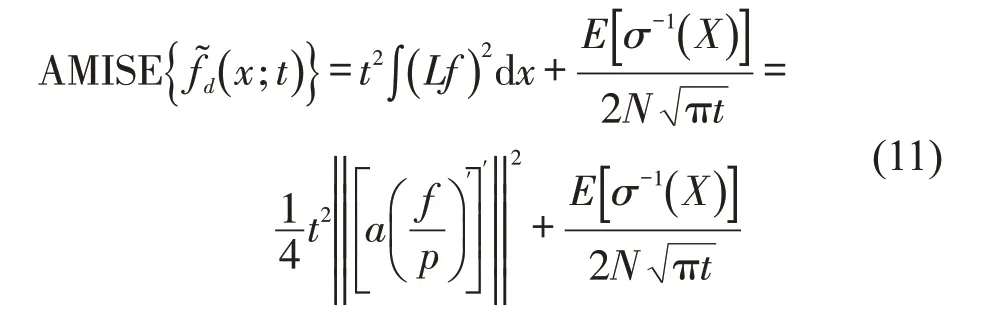
对式(12)求导，可以得到当AMISE取得最小值时所对应的最优带宽hopt为

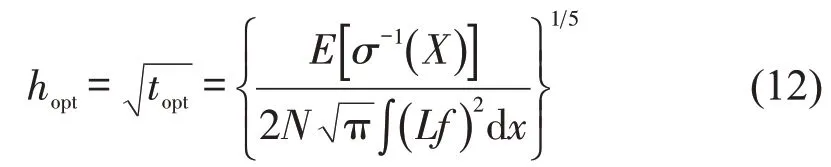
式中：hopt为最优带宽；。

2.4 拟合优度检验

为检验本文提出的自适应扩散核密度估计模型的准确性和有效性，选取卡方检验、K-S 检验以及后验检验3 项检验指标对概率分布拟合结果进行拟合优度检验。假设快速充电行为某一特征变量的假设经验分布函数为，累计分布函数为，3种检验指标的具体计算过程如下。

(1)卡方检验

卡方拟合优度检验方法是对样本的频数分布所来自的总体分布是否服从某种理论分布或某种假设分布所作的假设检验，电动出租车快速充电行为特征变量的总体分布是未知的，故可以采用最常用的卡方拟合检验方法，卡方检验统计量χ2为

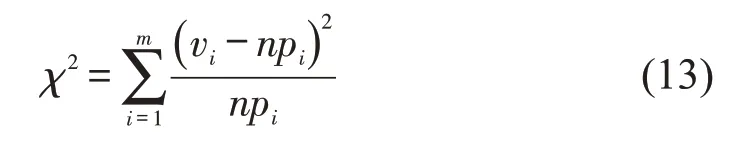
式中：n为特征变量对应的样本个数；m为将样本数据划分的区间个数；vi为第i个区间的观察频数；pi为第i个区间的理论概率值。

(2)K-S检验

Kolmogorov-Smirnov 检验，简称K-S 检验，主要用来检验一组样本数据的实际分布是否与某一指定的理论分布相符合。K-S检验统计量Dn为

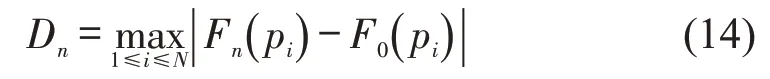
Dn值越小说明拟合优度越高。

(3)后验检验

为了更加直观对比各个概率分布模型的拟合优度，采用均方根误差RMSE估计概率分布模型与数据观测分布之间的差异。均方根误差的计算公式为

3 实例验证

出租车的交通功能定位是为城市内具有短途出行的乘客提供服务，由于乘客选择出租车出行的需求呈现明显的时空波动性，因此电动出租车的快速充电行为在时间维度和空间维度同样也具有明显的随机性。

3.1 不同时间维度的快速充电行为规律

本文主要研究电动出租车快速充电行为在时间维度上的差异性和规律性。首先，将时间维度划分为工作日和休息日，使用描述性统计分析充电起始SOC、充电结束SOC、充电前后SOC 变化量、充电起始时刻、充电持续时间这5个充电行为特征变量在工作日和休息日具有的差异性，得到描述性统计情况如表3所示。

表3 工作日和休息日快速充电行为特征变量的描述性统计Table 3 Descriptive statistics of characteristic variables of fast charging behavior

从表3可知，电动出租车工作日和休息日的快速充电行为存在较为明显的差异性，表现为工作日充电起始SOC比休息日充电起始SOC值要更低一些，工作日充电起始时刻比休息日要更晚一些，但是充电结束SOC、充电前后SOC 变化量等特征变量的区别不是很明显。为了更加直观地展示电动出租车充电行为规律在时间维度的差异性，采用本文提出的基于扩散方程的自适应扩散核密度估计模型对上述5个特征变量进行分布拟合，根据拟合结果可知：

(1)工作日和休息日电动出租车快速充电结束SOC、充电前后SOC变化量以及充电持续时间具有较为相似的规律，表现为95%以上的驾驶员会将电量充至99%，电量增加量大都集中在40%～85%，且充电持续时间集中在50～80 min。

(2)快速充电起始SOC和快速充电起始时刻在工作日和休息日具有显著的差异，其中起始SOC在工作日分布比较集中且均匀，有超过80%的电动出租车选择在车辆SOC 处于10%～50%时进行充电；相比工作日，休息日电动出租车充电起始SOC呈现显著的单峰，有超过55%的驾驶员选择在车辆SOC 处于40%～55%的时候进行充电，具体情况如图5所示；充电起始时刻工作日呈现出明显的波峰现象，但是16:00-23:00 分布较为平缓和均匀，表明这段时间充电数量较为稳定，非工作日呈现显著的“三峰”现象，分别是0:00-2:00、10:00-12:00、16:00-18:00，具体情况如图6所示。

图5 工作日和休息日快速充电起始SOC对比Fig.5 Comparison of SOC at beginning of fast charging between weekday and weekend

图6 工作日和休息日快速充电起始时刻对比Fig.6 Comparison of starting time of fast charging between weekday and weekend

3.2 不同概率建模方法的比较分析

验证本文提出的自适应扩散核密度估计模型应用于电动出租车充电行为特征变量建模的可行性。分别采用正态分布和极值分布这两种传统参数估计方法，采用常规核密度估计、文献[10]提出的基于边界核的自适应核密度估计和本文提出的改进核密度估计这3 种非参数估计方法对工作日快速充电起始时刻的概率密度进行估计。3种非参数核密度估计方法所得带宽、不同参数估计方法和非参数估计方法得到的概率分布模型的拟合优度检验结果如表4所示，快速充电起始时刻的直方图和各种概率分布模型的概率密度曲线如图7所示。

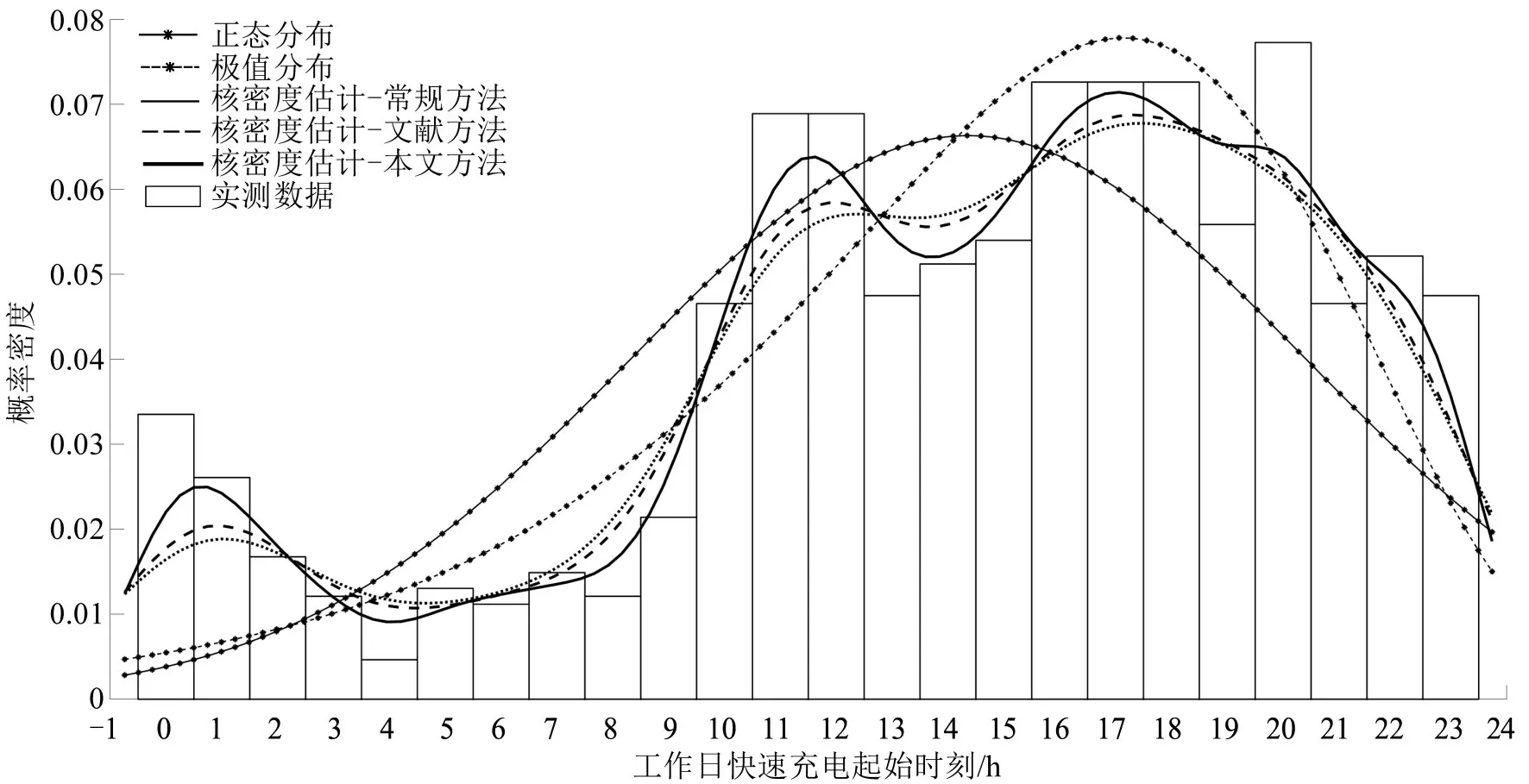
图7 工作日快速充电起始时刻的概率密度曲线Fig.7 Probability density curve of starting time of fast charging

表4 不同估计模型的拟合优度检验结果Table 4 Goodness of fit test results of different estimation models

根据表4 和图7 的直观展示可以得到如下结论：

(1)采用传统非参数估计方法对快速充电起始时刻进行概率分布建模时，得到的概率分布模型都未能通过卡方检验和K-S检验，同时概率密度曲线也未能很好地拟合样本数据的分布特征，特别是当样本数据存在多峰和不对称的情况。

(2)当采用不同核密度估计模型时，虽然常规核密度估计模型较之参数模型能准确反映电动出租车快速充电行为特征变量的分布规律，但在3种核密度估计模型中的拟合效果最差，故对常规核密度估计模型的修正和改进是非常必要的。

(3)本文提出的改进核密度估计方法能够通过各项拟合优度检验且各项检验指标的数值最小，同时该模型的概率密度曲线与实测数据的直方图拟合程度最好。

综上所述，本文提出的自适应扩散核密度估计模型在电动出租车快速充电行为特征变量的概率建模应用中具有很高的准确性和适用性。

4 结论

本文从电动出租车自身的角度出发，基于上海市电动出租车实测数据，使用Python进行原始数据的清洗和数据预处理，然后根据约束条件划分充电片段并从快速充电片段中提取充电起始SOC、充电结束SOC、充电前后SOC 变化量、充电起始时刻、充电持续时间等5 个快速充电行为特征变量。本文得到的主要结论如下：

(1)从不同时间维度对电动出租车充电行为规律进行研究时，工作日和休息日电动出租车快速充电结束SOC、充电前后SOC 变化量以及充电持续时间具有较为相似的规律，但是快速充电起始SOC和快速充电起始时刻在工作日和休息日具有显著的差异。

(2)对比现有研究常用的传统参数估计模型和核密度估计模型，选取卡方检验、K-S 检验和后验检验这3个指标作为拟合优度检验指标，验证了本文提出的基于扩散方程的自适应扩散核密度估计模型对于电动出租车快速充电行为特征变量的概率建模具有更高的拟合精度，表现为卡方检验和K-S 检验统计量远低于临界值，后验检验的RMSE值仅为0.00135。

此外，由于本文模型不依赖参数假设使其具有更高的稳健性和适用性。