基于建成环境和低频浮动车数据的路段行程时间估计

钟绍鹏，何璟，朱康丽，邹延权，隽海民

(1.大连理工大学，交通运输学院，辽宁大连116024；2.北京交通大学，交通运输学院，北京100044；3.重庆市交通规划研究院，重庆400000；4.大连市国土空间规划设计有限公司，辽宁大连116011)

0 引言

近年来，路段行程时间估计已经成为智能交通系统、交通需求预测与管理等方面研究的热点。路段行程时间估计方法起源较早，在各项研究中，有关路段行程时间估计的研究大多是通过复杂模型、数据分析方法以及仿真模型等进行的。

模型构建方面，Hellinga等[1]将总行程时间分解为行程路线上各个路段的行程时间。定义一个似然函数模型求解行程路线上每个路段的最可能行程时间；在此基础上，Jenelius 等[2]对参数进行极大似然估计，其中参数考虑了道路交通条件方面的因素；Dell'Orco等[3]提出一个基于时间的离散交通流模型，同时结合元启发式算法，提出一种全新的网络流量分配模型，提高了预测真实性。对于路段行程时间的估计问题，浮动车数据往往是用途较广、可靠性较高的方法之一。Hofleitner 等[4]结合浮动车数据，用极大似然估计法对各分布参数进行估计，使得估计的参数与历史浮动车数据观测的条件概率乘积成正比。除了建立统计模型以外，Zheng等[5]还利用探测车提取得到的低频浮动车数据以及实际路段行程时间数据，结合神经网络模型，对通过该路段车辆的完整路段行程时间进行了估计。近年来，路段行程时间的估计方法更趋于多样化，Ma 等[6]提出一种从路段行程时间分布中估计出行时间概率分布的广义马尔可夫链方法，并考虑时间和空间的相关性；Rahmani 等[7]结合斯德哥尔摩的出租车数据研究了路段行程时间估计的灵敏度，提出一种同时解决路径推理和行程时间估计问题的定点公式。此外，交通仿真在路段行程时间的估计中也有所应用，Liu等[8]利用明尼苏达大学开发的一个实时数据采集和存档系统，然后利用存档的交通数据，提出一种基于仿真模型的路段行程时间估计算法。

可以看出，现有基于建立模型进行估计的方法，大多结合交通流理论中排队论及延误等概念，在研究过程中考虑道路网中各种交通参数以及引起延误的各种交通因素；基于数据分析的方法一般是在大量数据基础上采用线性回归模型、贝叶斯网络模型、神经网络模型、卡尔曼滤波模型等科学方法进行相应研究[9]。

上述研究虽然能够实现对路段行程时间的估计，但是研究过程中更多考虑的是交通状态、道路参数及历史行程时间数据等，很少有研究者探讨建成环境属性因素对路段行程时间的影响。而建成环境会通过影响出行者的出行目的地、出行频率、出行方式、出行路线等方面，最终影响路段行程时间，这对城市交通规划与管理具有重要意义。因此，迫切需要建立一个考虑城市建成环境的路段行程时间估计模型，对建成环境影响进行定量刻画，从而进一步为路段设施改进提供相关依据。最近，Zhong 等[10]针对城市建成环境，分别应用全局回归模型和GWR模型对影响路段行程时间的主要因素进行深入研究，结合城市土地利用特性，有效解决了建成环境对路段行程时间影响的空间异质性问题。虽然在一定程度上解决了建成环境影响下路段行程时间的估计问题，但并没有针对行程时间在路段上的分布提出估计方法。此外，先前基于浮动车数据估计路段行程时间的研究往往需要收集车辆的速度、方向角等多种信息，而针对缺少上述信息的浮动车数据通常无法得到较好的估计结果。

鉴于此，本文以低频浮动车发送报告的位置数据为基础，建立建成环境因素与行程时间之间的函数关系，将周边包括学校、医院在内的各种设施以及下游交叉口等影响因素作为直接影响路段行程时间的变量，在不需要速度等GPS数据的条件下完成路段行程时间的估计。同时，与传统的基于GPS坐标和时间数据估计行程时间的方法不同，本文方法不需要对研究区域进行车辆路径推测与路径匹配，使用统计学方法建模，简化了计算过程，对于不同交通状况具有普遍适用性。此外，本文将研究路段划分为多个节段，研究路段行程时间的分布情况，用路段上浮动车车辆数分布情况代替距离作为路段行程时间分配系数，提高了路段行程时间估计结果的精度。最后，通过辽宁省丹东市振兴区锦山大街的实例来验证本文提出的方法并分析建成环境对路段行程时间的影响。

1 基于建成环境和低频浮动车的路段行程时间估计方法

浮动车系统是一项重要的区间交通参数检测技术[11]，利用GPS装置实时获取车辆的速度、位置、方向等信息，具有建设周期短、数据精度高、覆盖范围广、实时性强等优点，同时便于与车辆调度、监控系统共享GPS/GIS 基础数据。浮动车系统通过数据处理中心进行数据交互，数据处理中心利用地图匹配、路径推测等相关模型、算法对数据进行处理，建立浮动车位置数据和城市道路的时空关系，利用交通流理论等相关知识，最终得到浮动车所经过路段的行程时间等交通状态信息。本文使用浮动车发送报告的次数估计路段行程时间，故对所得数据包含的信息量要求较低，对于缺少速度、方向角信息的浮动车数据也可以进行估计。

1.1 建立发送报告次数与行程时间的关系

一般来说，在路段越拥堵、行程时间相对较长的路段上，浮动车发送报告的可能性越大，将浮动车在路段上发送报告这一事件作为随机变量，同时将路段划分成若干个节段，从而建立浮动车在各节段发送报告的次数与该节段行程时间之间的关系。

已知，浮动车发送报告的时间间隔是固定的，则每个浮动车在任意时刻发送报告的可能性一致，设浮动车在任意时刻发送报告的频率均为ε，则ε可表示为

式中：T为浮动车两次发送报告之间的时间间隔(s)；ε为浮动车发送报告的频率(s-1)。

将研究路段划分为K个节段，易知在任意一个节段xk内，浮动车在该节段xk汇报其位置的可能性ρx与该浮动车在该节段xk的行程时间t(xk)成正比，即

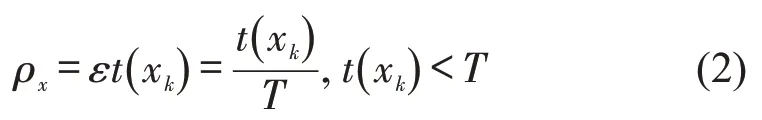
如果浮动车在某个节段处停留时间大于u个发送报告周期，即t(xk)＞uT，其中，u∈Z+,且，则u为最少发送报告的次数，其发送报告次数为u+1次的可能性ρux为

假设在研究的时间段内，路段的交通状态不变，也就意味着车辆在各节段的行程时间均相同。因此，把浮动车经过路段上每个节段都分别作为一个随机事件，假设浮动车在这一交通状态不变的时间段内的运行状态是无差异的，则可以认为多个浮动车经过节段是独立重复试验，服从伯努利分布。当时，在经过各节段的车辆总数m中发送报告的车辆数为nx的概率px为

式中：nx-mu为除去前u个周期内发送报告的次数后，在节段内再次发送报告的车辆数，且0＜nx-mu＜m，即mu＜nx＜m(u+1)，这里假设，在每一个节段，车辆发送报告的次数至多相差1 次，考虑到使用的是低频浮动车数据，这一假设比较合理。

1.2 路段行程时间与交叉口及建成环境的关系

根据路段长度，将路段划分为若干个节段，以往研究中，每一节段的行程时间，主要受节段的相关属性影响。节段属性包括该节段的长度、距离下游交叉口的距离等相关属性。在此基础上，本文特别考虑了建成环境对节段的影响，并使用节段到建成环境设施的距离来表示。

用一个线性结构表示与节段行程时间相关的共J种解释变量(包括路段属性、交叉口、附近的建成环境与土地利用等)对某一节段行程时间的影响，即

式中：Aj为影响节段行程时间的第j种解释变量值(m)，包括节段长度、节段距离下游交叉口或建成环境设施的距离等；αj为第j种解释变量对节段行程时间的影响程度(s·m-1)，为待估计的参数。具体关系如图1所示。

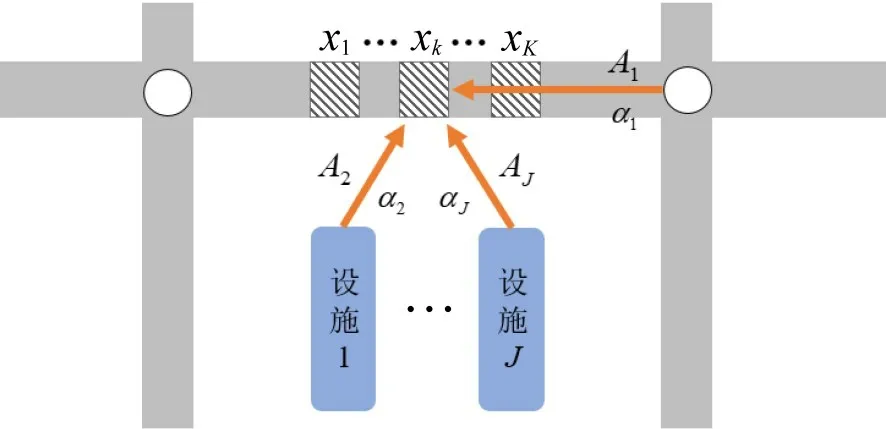
图1 节段行程时间影响变量Fig.1 Segment travel time influence variables

式(6)建立了路段行程时间与交叉口和建成环境之间的线性组合关系。于是估计各个节段的行程时间就转化成一个针对影响程度参数的极大似然估计问题，即

估计得到的结果是各参数的值，因而根据式(6)即可求出包括各类建成环境影响因素的节段行程时间，进一步再根据路段和节段的关系即可求出建成环境影响下的路段行程时间。

1.3 路段行程时间的分布

根据路段与节段的关系，路段上总的行程时间可以看作路段各节段行程时间的积分，即

式中：S为路段总长度(m)，ts为路段总行程时间(s)。因此可知，路段内某一段行程时间是此段内各节段行程时间的积分，即为第i段到路段起点的距离(m)。

可知观测到的在该节段发送报告的车辆数nx是期望的无偏估计，而浮动车在该节段的行程时间与浮动车在路段上各节段发送报告的可能性成正比。所以，可以认为浮动车在该节段的行程时间与浮动车在路段上各节段发送报告的次数成正比，即。进而对一定时间间隔内车辆发送报告的总次数进行统计，则各分路段的行程时间与路段总行程时间的比值等于在这一段车辆发送报告的次数与整条路段上车辆发送报告总次数的比值。

式中：Q1为第1段的行程时间与路段总行程时间的比值；t1为第1 段的行程时间(s)；l1、l2为第1 段和第2段到路段起点的距离(m)；为在节段xk车辆发送报告的次数(次)。

研究不同路段行程时间分布时，仍然沿用上述思路，即认为在相同交通状态下，车辆通过两条或多条路段的任意位置是一独立重复试验。两个路段行程时间的比值根据同时经过这两个路段的车辆在这两个路段上发送报告的总次数之比得到，即

式中：ts1、ts2分别为两路段的行程时间(s)；S1、S2分别为两路段的长度(m)。这样就可以得出所有路段之间行程时间的比值，也就解决了路段间行程时间分布问题。

2 实例分析

使用辽宁省丹东市内603 辆出租车共1868 万条实际浮动车数据，估计不同时段影响路段行程时间的各变量对应参数值，通过似然比检验说明建成环境对路段行程时间影响的显著性，将各分路段行程时间累计得到的完整路径行程时间与百度地图给出值进行对比，证明估计结果的合理性。

2.1 研究区域

研究区域位于丹东市振兴区锦山大街丹东市公共交通总公司一公司到丹东市环境科学研究院沿线附近，如图2所示。丹东市位于辽宁省东南部，是位于东北亚中心地带的沿海、沿江、沿边城市。锦山大街是丹东城市主干道，全长2.7 km，沿线共包括10 个交叉口，多数为环型交叉口和无信号控制交叉口，交通状况复杂，沿线有敬业高中、朝鲜族中学、福春街小学在内的多所学校，妇女儿童医院等医疗场所，以及加油站等便民设施，选择其作为研究建成环境对路段行程时间影响的对象十分具有代表性。

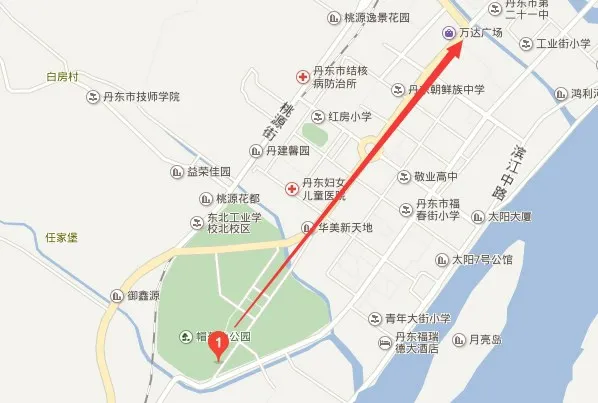
图2 研究区域Fig.2 Study area

2.2 参数选取与参数值估计

将路段划分为16 个节段，同时将各个节段长度设定为一个影响因素。其他影响行程时间的因素包括交叉口及周边建成环境。选取交叉口、学校、医院、诊所、加油站这5 类建成环境设施，并以各个节段到设施的距离作为变量。为体现到建成环境设施的距离越近，车辆通行受影响越大这一特征，把各变量取为距离的减函数。由于节段与设施间的距离远到一定程度时，可以忽略该设施的影响，因此认为距离建成环境设施大于1 km 的节段不再受影响。1 km 范围内各节段的距离变量值取为1-Ds/1000，Ds为设施到研究节段的距离(m)，而1 km 范围外各节段的距离变量取为0。对交叉口的处理是选取节段到下游交叉口的距离，且每一个节段仅有一个下游交叉口，故任意一个节段的交叉口变量个数应小于或等于1。

为便于观察参数值变化，已10 min划分时段间隔，故每10 min 得到1 组估计值，因6:00-6:30 得到的浮动车数据量较少，将这3 个时段合并为1 个时段。各变量值Aj代入式(7)和式(8)得到的参数结果如表1所示。

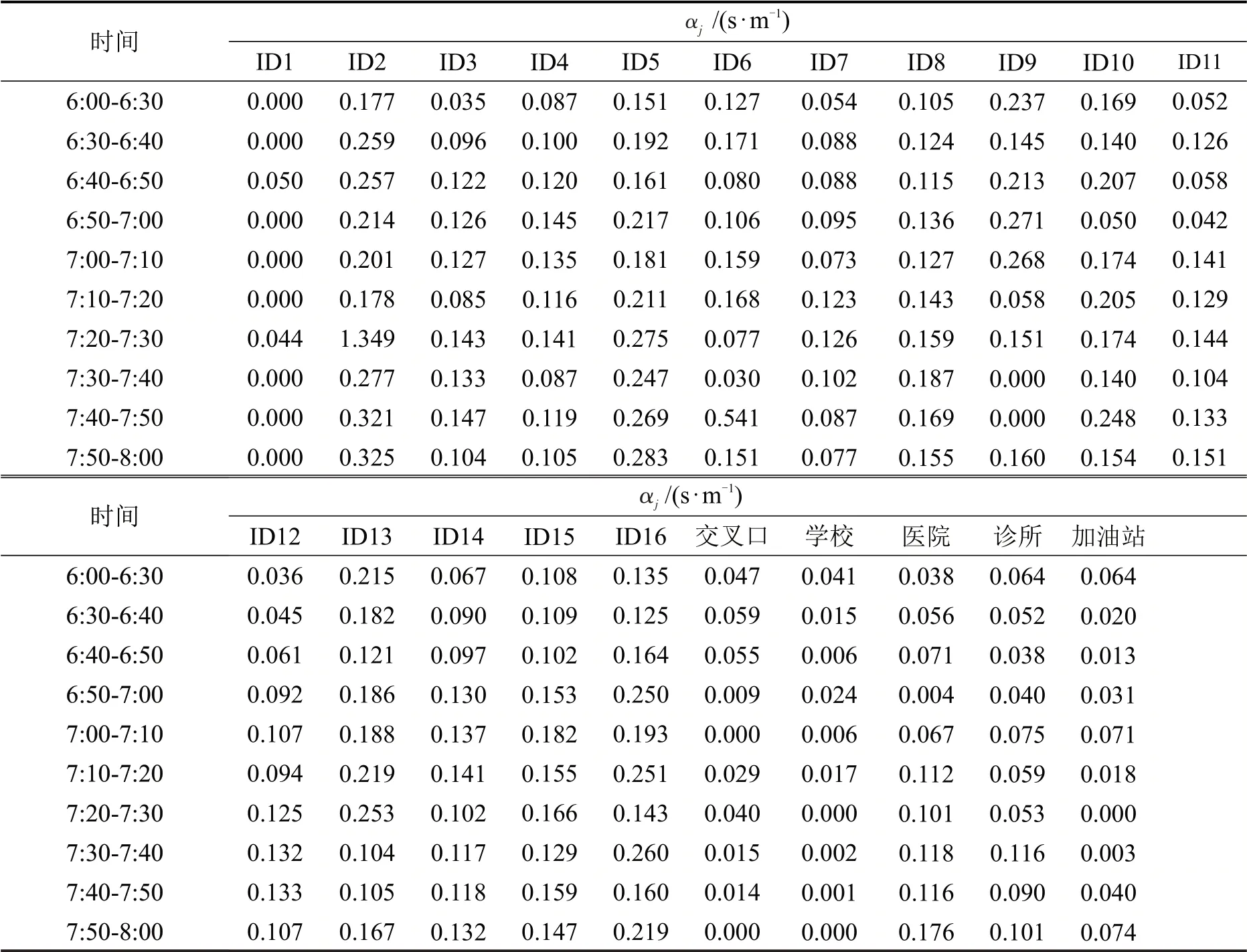
表1 行程时间各参数估计值Table 1 Estimated parameters about travel time

表1 中：ID1～ID16 表示锦山大街路段的16 个节段，考虑路段本身对行程时间的影响，使用这16个节段的长度进行参数估计；交叉口、学校、医院、诊所和加油站变量用来表示到建成环境设施的距离在1 km 以内时，由建成环境导致的影响程度参数平均值。

2.3 结果分析

如表1所示，所有变量的参数值均为正，验证了建成环境变量与路段行程时间是正相关的。随着路段行程时间增加，各建成环境对应的变量值并没有一个增加的趋势，这是因为在路段变得更加拥堵时，车与车之间的相互干扰也增加，使得建成环境的影响表现得相应较小。

此外，从表1 中可以看出，表示到交叉口距离变量所对应的参数值随时间的变动并不大，说明交叉口产生的延误在早高峰期间较为平均。由于研究范围内仅有一个交叉口为信号控制交叉口，故研究中未区分信号控制和无信号控制交叉口，多数交叉口实施无信号控制也说明交叉口交通状况基本良好。此外，表1中6:00-7:20学校所对应的参数值相对其他时段较大，体现了学生上、下学产生的机动车停车以及其周围人流量增加对道路行程时间的影响。

与医院对应的变量中同样也可以看出，其参数估计值在一定时段内有上升趋势，但人们到医院就医时间相对学生上学较晚，其出现上升趋势的时间与学校变量相比较为滞后，尤其是在7:00之后较为明显，因有些医院门诊7:30-8:00 开始上班，这说明就诊人流量的增加引起医院周围路段延误的增加。而医院变量比其他变量的参数估计值大，这可能是因为医院正门朝向一般为城市主干道路，而学校尤其是小学、幼儿园由于教学环境要求，朝向一般为支路；此外，进出医院的人更愿意乘坐私家车、出租车，车辆停车造成的延误更加显著。

2.4 参数值检验

本文采用似然比检验评估建成环境解释变量的合理性。 似然比检验公式为RLR=，其中，RLR为似然比检验值，L1为添加建成环境解释变量的极大似然值，L2为无建成环境变量的极大似然值。得到似然比为

且对于多参数的似然比可知，RLR=-2 ln(λ) 服从χ2分布。

此外，为了检验两个模型似然值的差异是否显著，还需考虑自由度。常用的似然比检验中，自由度等于在复杂模型中增加模型参数的数目，本文为新增的建成环境解释变量数，即自由度为5。

进而根据χ2分布临界值表就可以判断建成环境的影响是否显著。对无建成环境解释变量的极大似然函数值与添加建成环境解释变量的极大似然函数值分别取对数的相反数进行对比，如表2所示。

表2 有无建成环境解释变量的似然比检验Table 2 Likelihood ratio test of built environment explanatory variables

2.5 路段行程时间计算

用所得参数，根据式(6)～式(8)计算沿锦山大街丹东市公共交通总公司一公司至丹东市环境科学研究院的行程时间，结果如表3 和图3所示。整体上看，锦山大街路段行程时间在6:00-8:00之间呈现了一个增加的趋势，与实际早高峰现象相符；在接近7:30 时开始出现回落，此时车辆在路段上的行程速度逐渐增大。

图3 行程时间变化图Fig.3 Changes of travel time

将表3 中估计所得时间与百度地图所测得的“全长约2.8 km，大约需要5 min”的行程时间进行比较，结果基本吻合。从6:00 开始，该路段的行程时间逐渐增加，这也与实际情况相符，进一步验证了考虑建成环境对路段行程时间影响的合理性。

表3 行程时间随时间变化Table 3 Changes of travel time with time goes by

3 结论

本文将建成环境作为路段行程时间的解释变量，以浮动车发送报告的位置数据为基础，使用统计学方法建模，在不需要速度等GPS 数据、不需要对研究区域内浮动车进行路径推测与路径匹配的条件下构建了建成环境因素与行程时间的函数关系，并验证了建成环境因素对路段行程时间的影响。以丹东市振兴区锦山大街为例进行证明。结果说明，建成环境的影响对车辆的路段行程时间具有较为显著的增加作用。其中，学校的影响主要在6:00-7:20这一时间段，医院、诊所则集中在7:00-8:00，而交叉口产生的路段行程时间增量整体较为平均。本文中建成环境对路段行程时间产生的影响，是由于高峰期上学、就医、加油导致的车辆频繁进出和停车造成的，借助本文结论可以对学校、医院等设施的车辆进出与停车实施更加规范的交通管理措施，以保障车辆正常通行。同时，本文还给出一种路段行程时间分布的估计方法，该方法可用于在建立路段行程时间历史数据库后，使用路段上浮动车车辆数的分布情况代替距离作为路段行程时间的分配系数，从而对路段行程时间的分布情况进行估计，提高了路段行程时间估计结果的精度。本文利用信息量较为单一的浮动车数据实现了建成环境影响下的路段行程时间估计，可为该领域研究提供参考。