指向学生自主学习的高中数学探究式教学策略

庄子娟

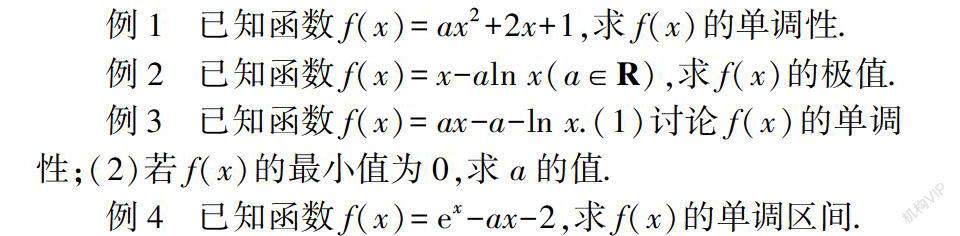
【摘要】高中数学新课程标准凝练了学科核心素养，提出把握数学本质，启发思考，改进教学.本文基于学科核心素养的视角，提倡以弘扬人的主体性、能动性、独立性为宗旨的自主学习，并对高中数学探究式教学模式进行一些反思和实践.

【关键词】学科核心素养;自主学习;学案;翻转课堂;探究式教学

《普通高中数学课程标准（2017年版）》提出，高中数学教学应以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质，提倡独立思考、自主学习、合作交流等多种学习方式.促进学生自主学习需要教师不断探索新的教学模式，下面笔者就针对学生自主学习的探究式教学谈谈自己的一点体会和思考.

一、以学案为载体的探究式教学

数学抽象是新课程的核心素养之一.数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养.下面是笔者尝试以培养学生核心素养为导向，以学案为载体的探究式学科教学.

案例1 高中数学选修1-1“导数及其应用复习”（第一课时）

片段一：【数学思想 追本溯源】

以学案为导向阅读课本，思考在数学学习中最打动人心的问题：概念和原理是如何产生的？将两章整合在一起进行复习.

问题1：导数的概念是如何产生的呢？

（设计意图：用学案引导学生从旧知识习得新的收获，借助思想方法，追本溯源，对导数这两章的知识进行再次梳理.）

问题2：导数的应用体现在哪些方面？

（设计意图：引导学生追本溯源，发现用导数研究函数的单调性是导数在数学上最重要的应用之一.这对深入研究函数的其他性质起着至关重要的作用，渗透着极限思想和数形结合思想.同时，我们运用极限思想、转化思想可以进一步分析导数在实际问题中的相关应用.）

片段二：【导数应用 追本溯源】

问题3：函数的单调性是函数最重要的性质之一，是导数在数学其他方面应用的基础.如何用导数这个“利器”解决函数的单调性问题呢？

（设计意图：引导学生观察利用导数求函数单调区间的步骤，逆向分析函数的单调区间：要求函数的单调区间，要先研究导函数在区间的正负性，为了得到导函数在区间上的正负性，必须先研究导函数的图像.）

问题4：如果导函数含参数的话，怎么才能画出导函数的大致图像呢？（分类讨论思想）

（设计意图：引导学生从平时做过的相关题目中观察、发现并总结归纳，以学案的问题串为导向，引导学生思考得到含参导函数形式的两种类型：一次函数类型、二次函数类型.）

片段三：【典例分析 类型溯源】

问题5：观察例1中求得的导函数，发现参数a在x的系数中，我们借助一次项系数与0的比较确定参数a分类讨论的临界值.参数a如果在导函数的其他位置又如何确定它的临界值呢？是否可以用刚才研究例1的方法来继续研究例2呢？

例1 已知函数f（x）=ax2+2x+1，求f（x）的单调性.

例2 已知函数f（x）=x-aln x（a∈R），求f（x）的极值.

例3 已知函数f（x）=ax-a-ln x.（1）讨论f（x）的单调性;（2）若f（x）的最小值为0，求a的值.

例4 已知函数f（x）=ex-ax-2，求f（x）的单调区间.

（设计意图：通过对导函数含参的一次函数类型的原函数单调性的初步探究，使学生经过例题变式，层层递进地探究出研究问题的方法，找到確定参数分类讨论的临界值的方法，完成学案的“总结引导”，体验从特殊到一般再到特殊的学习规律，激发学生自主探究的学习精神.）

提炼方法：（确定参数分类讨论的临界值）

先看定义域→求导，找出导函数或所需函数→确定参数分类讨论的临界值→分析导函数或所需函数的零点，画出导函数或所需函数的图像→找到原函数的单调区间.

问题6：导函数为含参的二次函数类型是否也可以用同样的方法分析原函数的单调性呢？

求函数f（x）=13x3+x2+ax+1（a∈R）的单调区间.

（设计意图：借助学案的“思考引导”引导学生类比导函数为含参的一次函数类型，继续探究导函数为含参的二次函数类型的情况，为复习课的第二课时做铺垫.）

通过学案中的“学习引导”“思考引导”“总结引导”“拓展引导”对导数及其应用的知识进行梳理，让学生真正在自主学习中完成相关问题的解决，培养学生用归纳整理、极限思想、数形结合和分类讨论等思想理解和解决问题的能力，真正实现学案与教学相结合的数学课堂.

二、基于翻转课堂创新模式的探究式教学

“互联网+”时代的来临，正在逐渐改变课堂教与学的先后顺序，而信息技术的发展为翻转课堂的教学模式研究与实施提供了支撑.翻转课堂是一种以学生为中心的教学模式，强调学生先学教师后教的个性化学习，重点是学生在课下自学，教师由授课转为引导.本研究的创新在于如何充分发挥学校的信息技术优势，将微课与翻转课堂很好地融合在一起，实现学生自主化学习、模块化学习和个性化学习的新探究式教学.

案例2 选修2-1第三章§4.1“曲线与方程”（第一课时）

（一）先学任务单（含先学微课）

1.阅读初尝试

（1）阅读本章中椭圆、抛物线及双曲线的标准方程推导，回顾必修2中直线的点斜式、圆的标准方程的推导.思考：为什么求出方程后，还要给出“以这个方程的解为坐标的点都在曲线上”的证明？

（2）观察下列曲线和方程，思考问题.

点与解一样多

① 方程可不可以作为相应曲线的方程？

② 方程的解和曲线的点存在什么联系？

③ “曲线的方程”“方程的曲线”的定义是什么？