例谈导数求参问题中的渐近线

黄江威

摘 要：通过对两个导数综合题目求參问题的讲解，呈现渐近线在解题中不可忽视的地位与作用，对今后教学如何更好地引导学生严谨作图起到抛砖引玉的作用。就函数图象的渐近线问题，通过几个函数求参问题解析中渐近线的应用，更好地体会数形结合求参问题中渐近线的地位，今后教学中注意适时地做好渗透，提升学生作图解题的严谨性。

关键词：数形结合;渐近线;综合应用

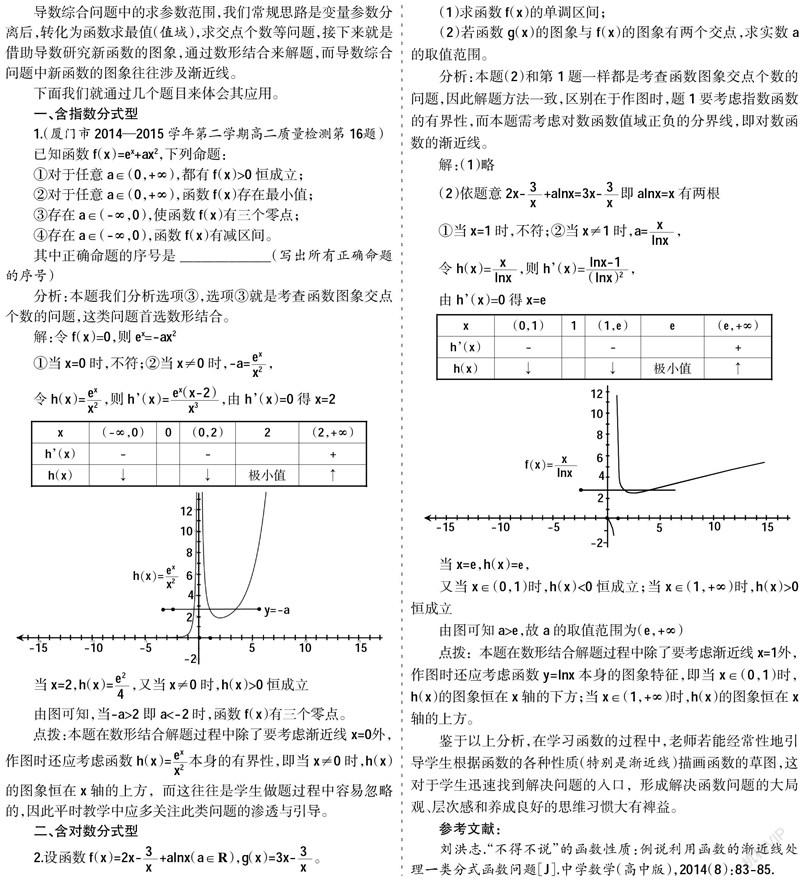
导数综合问题中的求参数范围，我们常规思路是变量参数分离后，转化为函数求最值（值域），求交点个数等问题，接下来就是借助导数研究新函数的图象，通过数形结合来解题，而导数综合问题中新函数的图象往往涉及渐近线。

下面我们就通过几个题目来体会其应用。

一、含指数分式型

鉴于以上分析，在学习函数的过程中，老师若能经常性地引导学生根据函数的各种性质（特别是渐近线）描画函数的草图，这对于学生迅速找到解决问题的入口，形成解决函数问题的大局观、层次感和养成良好的思维习惯大有裨益。

参考文献：

刘洪志.“不得不说”的函数性质：例说利用函数的渐近线处理一类分式函数问题[J].中学数学（高中版），2014（8）：83-85.