螺旋槽小孔节流动静压气体轴承动态特性分析*

李树森 王欣崎 李 博 贾 勇

(东北林业大学机电工程学院 黑龙江哈尔滨150040)

气体轴承因其摩擦小、精度高、寿命长、温度变化平缓等特点而广泛应用，然而气体轴承在高速工作时，容易出现涡动失稳现象，可能会导致轴承发生碰磨甚至失效[1-4]。通过开设螺旋槽等可以增加轴承的动态效应从而提高稳定性，但是仅依靠轴承本身产生动压效应来提高稳定性是非常有限的[5-8]。因此，研究轴承的动态特性对如何提高轴承稳定性是十分关键的。

戚社苗等[9]通过数值仿真计算动压气体轴承的动态特性系数，并重点研究轴颈扰动频率和不同轴颈扰动频率下轴承的静压承载及轴承数对动态特性系数的影响。张皓成等[10]分析供气压力和气膜厚度对圆盘型单个小孔节流气体静压止推轴承静动态特性的影响。贾晨辉等[11]为改善球面螺旋槽动静压气体轴承的动态特性，研究气膜涡动和振荡的力学机制。陈东菊等[12]基于空气静压轴承的非线性动态特性，研究空气静压主轴的振动特性和预测模型，探索非线性动态特性分析对主轴回转精度的影响并研究空气静压主轴的振动特性。姚英学等[13]采用小扰动法进行狭缝节流球形静压气体轴承的动态特性研究，仿真分析动态特性系数随各参数的变化规律。

螺旋槽小孔节流动静压气体轴承，将螺旋槽产生的动压效应与小孔节流产生的静压效应相结合，有可能进一步改善轴承的稳定性。本文作者以螺旋槽小孔节流动静压气体轴承为研究对象，建立计算分析模型，求解动态特性系数[14-15]，并研究各参数对轴承动态特性的影响，为进一步提高轴承稳定性提供理论基础。

1 计算分析模型

1.1 几何模型的建立

图1为螺旋槽小孔节流动静压气体轴承结构示意图，其中：ps为供气压力；pa为环境压力；d为主轴直径；n为主轴转速；e为偏心量；h为气膜厚度。D为轴承外径；L为轴承长度；l1为孔边距；ds为节流孔直径；bg为螺旋槽宽度；hg为螺旋槽深度。

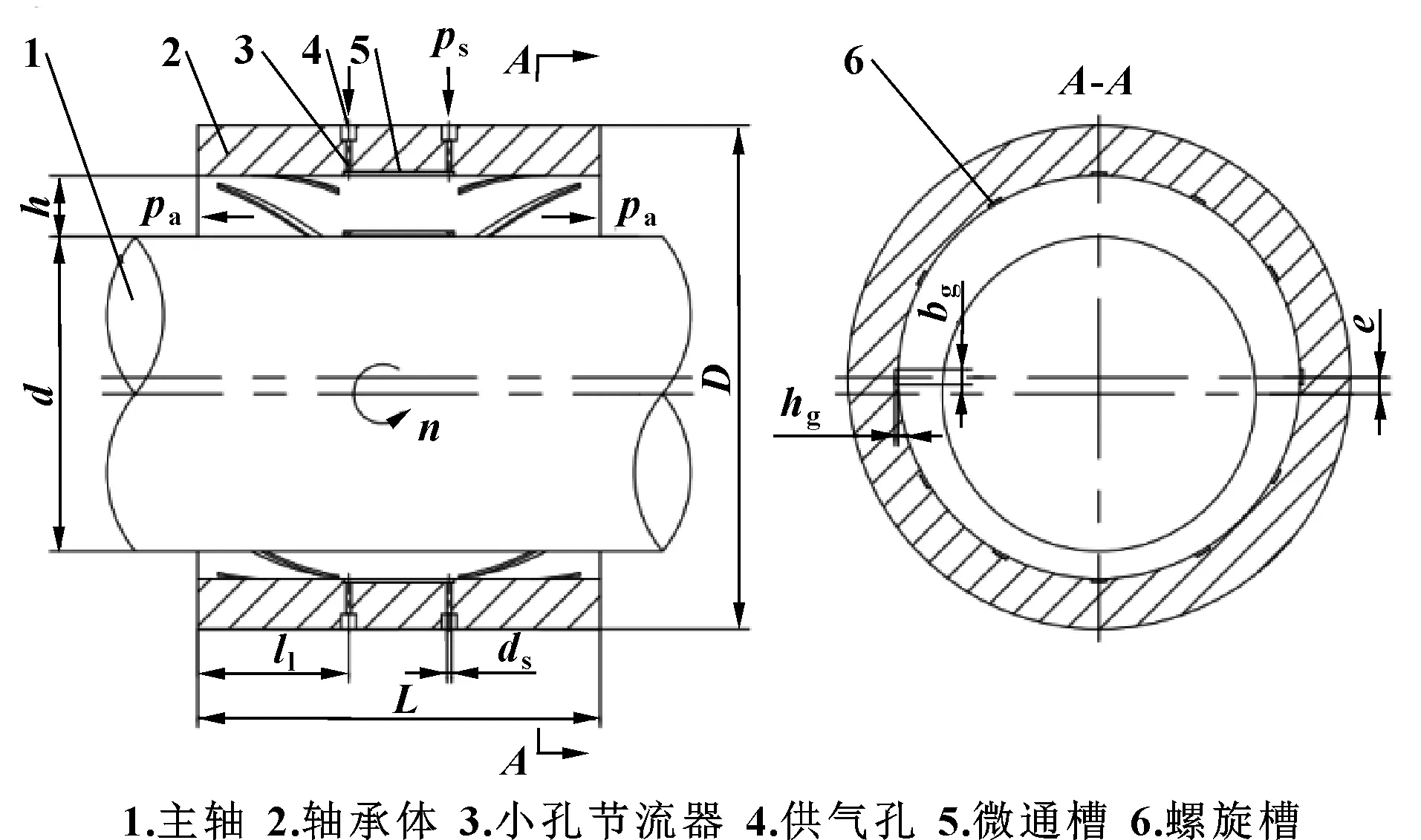
图1 螺旋槽小孔节流动静压气体轴承结构示意Fig 1 Schematic of spiral groove small orificethrottle hybrid gas bearing structure

1.2 润滑分析数学模型

螺旋槽小孔节流动静压气体轴承的动态分析直接依赖于动态条件下的压力分布和气膜厚度，则应以不定常工况下的雷诺方程[16]作为分析计算基础。在圆柱坐标系中有如下量纲一化形式雷诺方程：

(1)

在小扰动情况下，量纲一气膜压力分布和量纲一气膜厚度为

(2)

式中：P0为静态气膜压力；Pd为动态气膜压力；i为复数单位；Pd0为定义在复数范围内的动态气膜压力幅值；H0为静态气膜厚度，H0=1+ε0cosφ(ε0为静平衡位置时的偏心率)；Hd为动态气膜厚度；Hd0为定义在复数范围内的动态气膜厚度幅值。

将式(2)代入方程(1)中并化简，略去高阶项后得到气体润滑动态雷诺方程的一般形式，如方程(3)所示。

i2Λγ(H0Pd0+Hd0P0)

(3)

采用有限差分法离散方程(3)，即可求得气膜压力。

2 模型求解

2.1 扰动压力的推导

图2示出了轴承中主轴在偏离稳态位置时的受力情况，其中：Ob为轴承中心；Oj为主轴中心；O′j为偏离稳态时的主轴中心；e为偏心距；θ为偏位角；Fξ为使轴心绕平衡点做涡动运动的促涡分力；Fφ为使轴恢复平衡的恢复力。

图2 轴承中轴的受力关系Fig 2 The force relationship of the shaft in the bearing

轴心在变位运动时的动态压力分布为

(4)

轴心在定常工况下静平衡位置的压力分布为

P=P(φ,ξ;e0,θ0;0,0)

(5)

采用偏导数法得到扰动压力为

(6)

2.2 动态刚度、动态阻尼的求解

气膜的动态特性表现为主轴在外部随机扰动下偏离静平衡位置，在其附近做变位运动时气膜力的相应变化情况。对动态压力分布公式(4)进行积分，得到轴心做变位运动时各方向的气膜力为

(7)

气膜力表达式(7)对轴心位移和变位速度求偏导，得到气膜的动态刚度表达式(8)和动态阻尼系数表达式(9)。

(8)

(9)

式中：Kij为量纲一动态刚度系数；Cij为量纲一动态阻尼系数；i表示气膜力增量方向；j表示轴心位移增量方向；下标0为气膜压力对静平衡位置求导。

将定义在式(8)和式(9)中的动态刚度和动态阻尼系数转换到直角坐标系，如式(10)和(11)所示。

(10)

(11)

式中：Kxx、Kyy为直接刚度；Kxy、Kyx为交叉刚度；Cxx、Cyy为直接阻尼；Cxy、Cyx为交叉阻尼。

3 计算结果及分析

研究的轴承的参数如下：D=100 mm；d=80 mm；L=80 mm；ds=0.2 mm；h0=15 μm；l1=30 mm；hg=45 μm；bg=3 mm；pa=0.1 MPa；ps=0.6 MPa；ε=0.5；n=120 000 r/min。为了准确得到参数变化对轴承动态特性的影响，在其他参数保持不变的情况下，分别仿真分析了涡动比、供气压力、转速以及槽宽和槽深对轴承动态特性的影响。

3.1 有槽和无槽情况下涡动比对轴承动态特性的影响

为研究螺旋槽的影响，文中同时建立了无螺旋槽小孔节流动静压气体轴承模型，对比研究了有槽和无槽情况下不同涡动比对动态刚度和阻尼的影响规律，结果如图3所示。

由图3可知，相比无槽情况，有螺旋槽可以使轴承产生动压效应，从而提高轴承的动态特性。其中直接刚度Kxx、Kyy大幅提高，交叉刚度Kxy、Kyx提高较小；直接阻尼Cxx、Cyy和交叉阻尼Cxy、Cyx都有所提高，总体上提高了轴承稳定性。在有槽和无槽情况下，各刚度和各阻尼系数随涡动比的变化趋势相同。随涡动比增大，直接刚度Kxx、Kyy增大，交叉刚度Kxy、Kyx减小；当涡动比大于1后，直接刚度Kxx、Kyy增速减慢，而交叉刚度Kxy、Kyx在有槽和无槽情况下均相差不大且都趋近于0。直接阻尼Cxx、Cyy和交叉阻尼Cxy、Cyx随着涡动比的增大逐渐减小并趋近于0。

3.2 转速对轴承动态特性的影响

转速是轴承稳定工作的重要参数，从图4所示的转速对轴承动态刚度和阻尼的影响规律曲线可知，各刚度系数随转速增大而增加，因此主轴受扰时恢复稳定工作的能力也增强；但当转速大于120 000 r/min后，各刚度系数的增速均减缓。各阻尼系数均随转速的增大而减小，且与转速呈线性关系，因此动态阻尼对气膜涡动的抑制作用逐渐减弱，当气膜涡动力大于动态阻尼时，出现涡动失稳现象。因此，气膜的稳定状态需从刚度和阻尼的综合作用考虑。

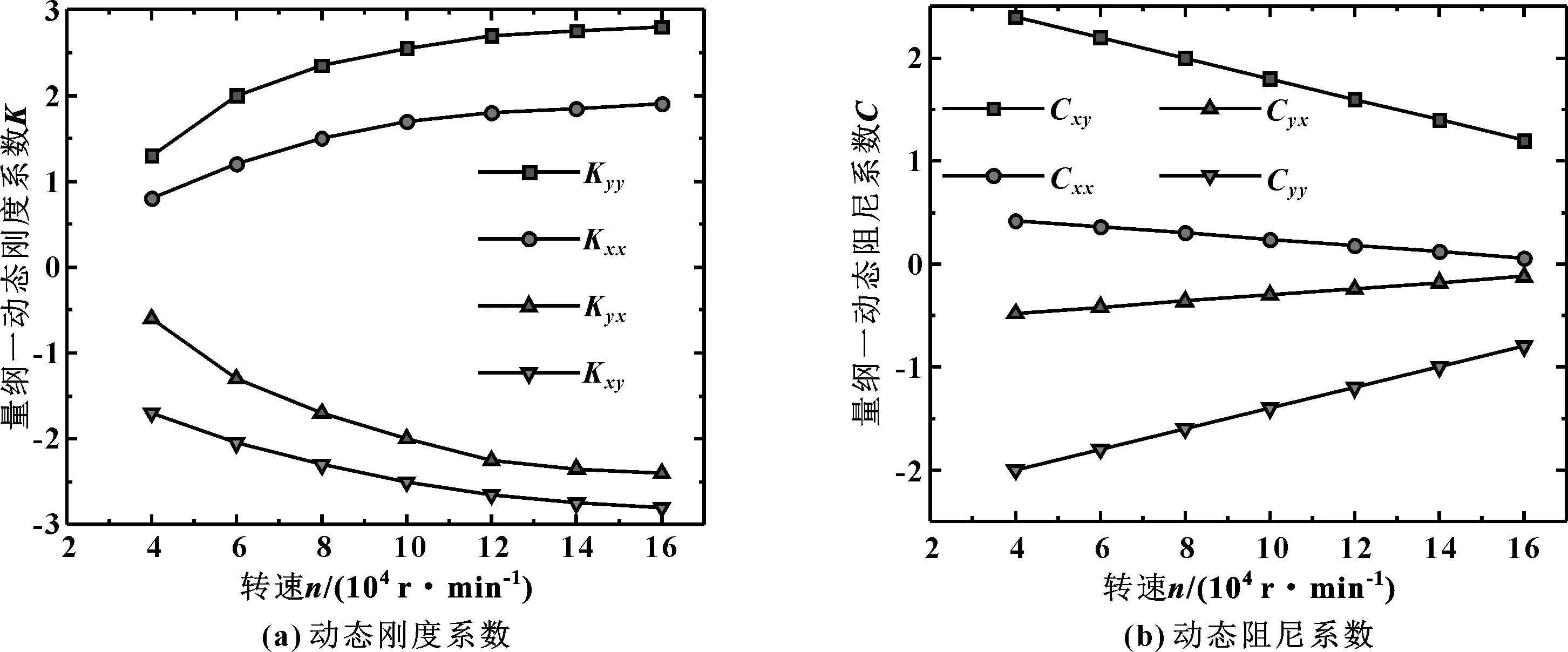
图4 转速与动态刚度和阻尼的关系曲线Fig 4 The relation between rotational speed and dynamic stiffness and damping(a)dynamic stiffness coefficient;(b)dynamic damping coefficient

3.3 供气压力对轴承动态特性的影响

供气压力不仅对轴承静态特性有影响，同时也会影响轴承动态特性。保持其他参数不变，研究在不同供气压力下动态刚度和阻尼的变化情况，如图5所示。

由图5可知，供气压力对动态刚度和阻尼的影响趋势相同，供气压力增大，各刚度和各阻尼系数都随之增大，其中直接刚度Kxx、Kyy快速增大，而交叉刚度Kxy、Kyx相对增速较慢，当供气压力大于0.5 MPa后，各刚度系数呈缓慢增大趋势；交叉阻尼Cxy、Cyx受供气压力影响较弱，而直接阻尼Cxx、Cyy相对变化明显。上述结果表明，供气压力越大越有利于提高轴承动态特性，从而减小涡动提高轴承稳定性。但供气压力过大，会使轴承产生自激共振现象，可能导致轴承工作失常、严重损伤，乃至抱轴。

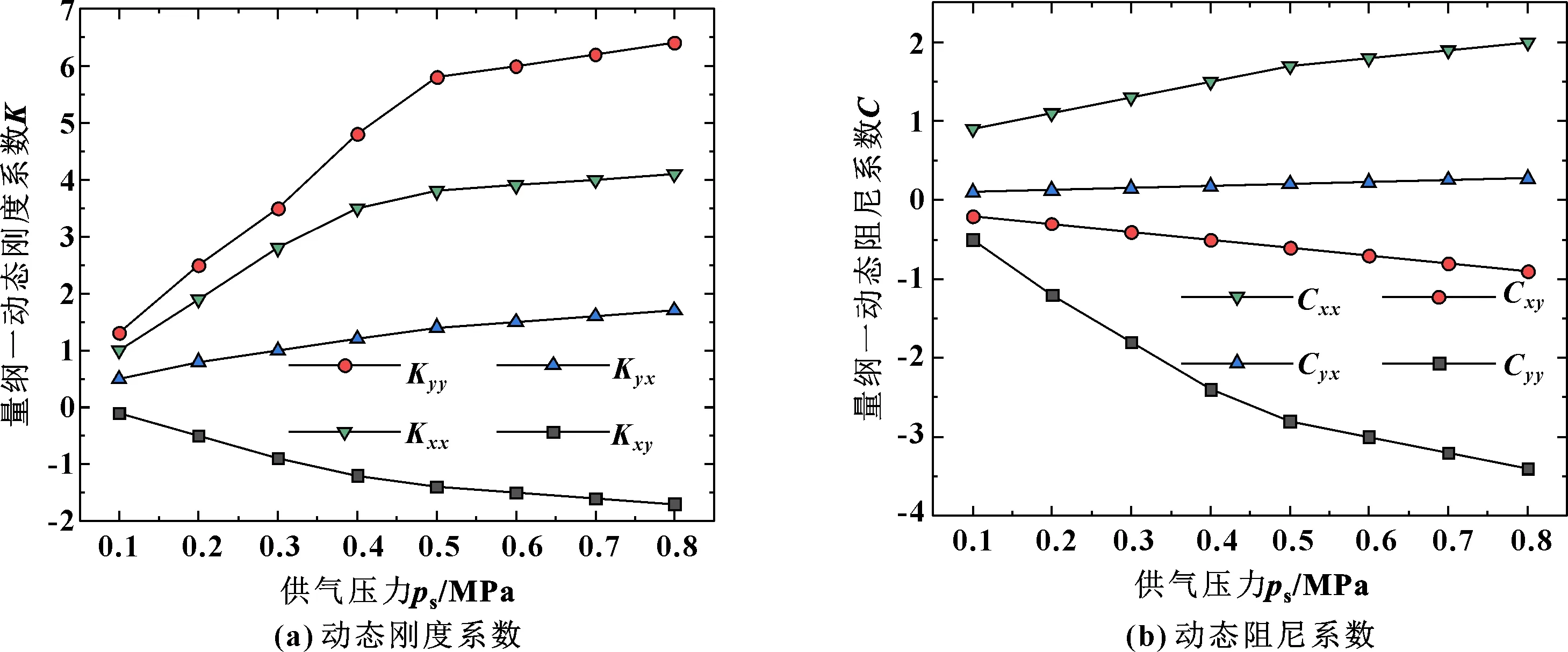
图5 供气压力与动态刚度和阻尼的关系曲线Fig 5 The relation between air supply pressure and dynamic stiffness and damping(a)dynamic stiffness coefficient;(b)dynamic damping coefficient

3.4 螺旋槽参数对轴承动态特性的影响

前文研究表明，螺旋槽能增加轴承稳定性，因此螺旋槽参数变化也会影响轴承动态特性。分别改变螺旋槽宽度和深度，得到动态刚度和阻尼的规律曲线，如图6、7所示。

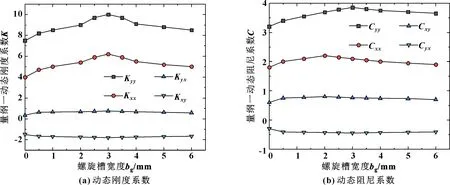
图6 螺旋槽宽度与动态刚度和阻尼的关系曲线Fig 6 The relation between spiral groove width and dynamic stiffness and damping(a)dynamic stiffness coefficient;(b)dynamic damping coefficient

由图6可知，各刚度和阻尼系数有槽时的数值都比无槽时(即槽宽为0时)显著提高；随着槽宽的增加，直接刚度Kxx、Kyy和直接阻尼Cxx、Cyy呈先增大后减小的趋势，但槽宽对交叉刚度Kxy、Kyx和交叉阻尼Cxy、Cyx的影响较小；当槽宽趋近于2时，直接阻尼Cxx达到最大值；当槽宽趋近于3时，直接刚度Kxx、Kyy和直接阻尼Cyy达到最大值。

由图7可知，在有槽情况下，各刚度和阻尼系数比无槽情况(即槽深为0时)的数值增加，且当槽深小于45 μm时，随着槽深的增大，直接刚度Kxx、Kyy和交叉刚度Kxy、Kyx也不断增加；当槽深大于45 μm时，直接刚度Kxx、Kyy增加趋势变缓，而交叉刚度Kxy、Kyx呈减小趋势。各阻尼系数都随槽深的增大先增加后减小，在槽深等于45 μm左右出现极值点，并且直接阻尼Cxx和交叉阻尼Cyx的变化趋势相对较小。

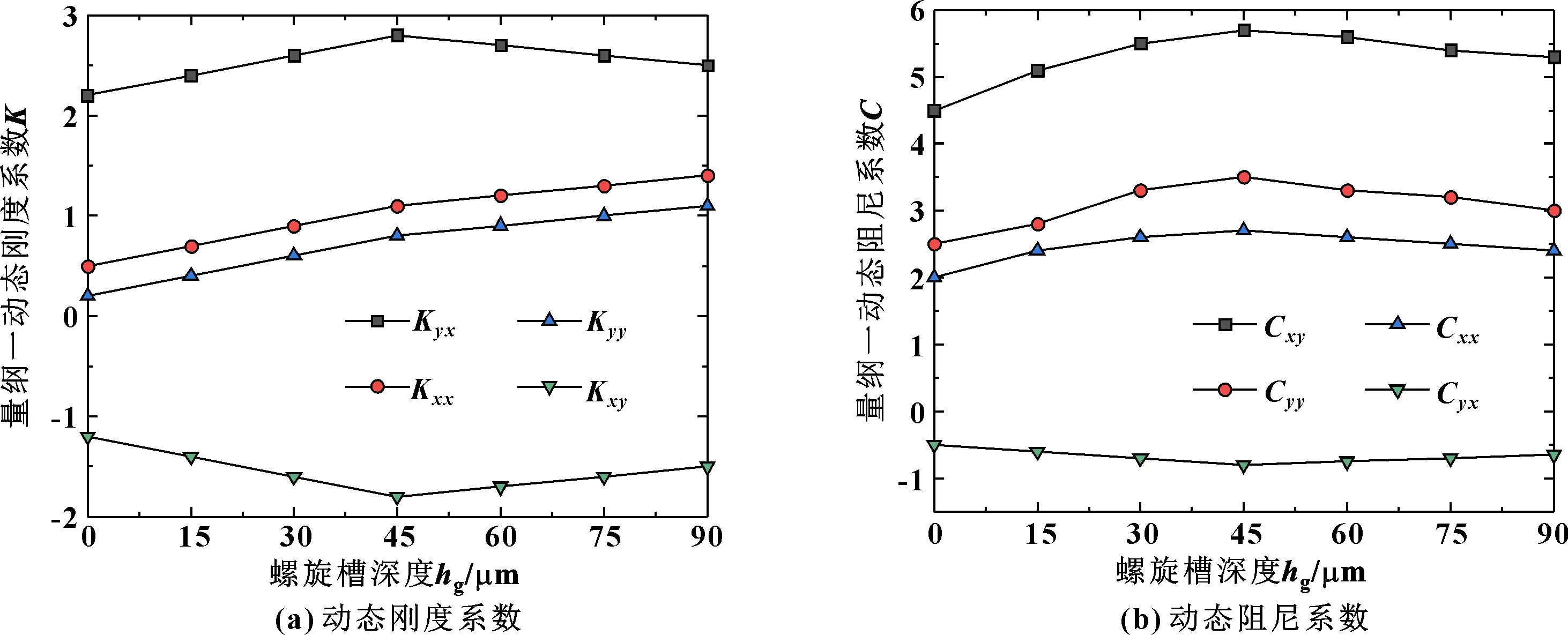
图7 螺旋槽深度与动态刚度和阻尼的关系曲线Fig 7 The relation between spiral groove depth and dynamic stiffness and damping(a)dynamic stiffness coefficient;(b)dynamic damping coefficient

3.5 仿真结果验证

为确定仿真结果的有效性，将部分仿真结果同理论求解结果进行了对比，如图8所示，可知仿真结果与理论求解结果具有很好的一致性，只存在微小差异，表明文中的仿真结果是可信的。

图8 仿真结果与理论求解结果对比Fig 8 Comparison of simulation results and theoretical solution results (a)dynamicstiffness coefficient;(b)dynamic damping coefficient

4 结论

(1)螺旋槽可以显著提高轴承的动态特性，增加轴承的稳定性。

(2)随涡动比的增大，直接刚度增加，交叉刚度和各阻尼系数都减小并趋近于0；随转速的增大，各刚度系数增加，而各阻尼系数减小；供气压力越大，各刚度系数和各阻尼系数越大，但供气压力过大可能会产生自激共振现象。

(3)随槽宽的增大，直接刚度和阻尼呈先增加后减小趋势，交叉刚度和阻尼变化较小；随槽深的增大，直接刚度增加，交叉刚度和各阻尼系数先增加后减小。