考虑硬度变化的结合面法向接触刚度分形模型*
王颜辉 张学良 温淑花 陈永会
(1.太原科技大学机械工程学院 山西太原 030024; 2.山西能源学院机电工程系 山西晋中 030600)
机械零部件之间通过装配形成的结合面,在机械系统正常运行过程中起着极其重要的作用。结合面在微观尺度下呈现为不同曲率半径和高度的微凸体,结合面间的接触是不连续的且仅发生在较高的微凸体上,导致真实接触面积与名义接触面积相差甚远,造成大载荷作用于小接触面积的状况,因此结合面间接触性质、应力分析等的研究非常复杂[1]。研究结合面之间的接触变形行为和精确建模对于深入了解摩擦、磨损、润滑、导电、导热等机制非常重要。
国内外学者在结合面接触行为的研究上已经做了不少工作,研究方法主要是建立理论模型,其中统计学分析和分形理论为2种最常用的主导求解方法。由于统计学参数,很大程度上受到粗糙度测量仪的分辨率或滤波器等因素的影响,因此对于一个粗糙表面来说不具有唯一性。
分形模型最早是1990年提出的MB模型,该模型认为随着载荷增大,微凸体的变形过程为塑性变形到弹性变形过渡,这与传统的接触研究相反[2-4]。此后基于MB分形模型研究人员又进行了很多的研究,进而获得更加准确的结合面接触力学特性。MORAG和ETSION[5]建立了单个微凸体的弹塑性接触分形模型,对MB模型中微凸体由塑性到弹性的变形顺序与经典赫兹接触理论相矛盾的问题进行解答,其结论证明单个微凸体临界接触面积的尺度相关性。田红亮等[6]对CEB模型进行了进一步修正,考虑了在弹塑性阶段材料硬度随表面深度的变化,建立了一种结合面单次加载分形模型。然而该模型在微凸体弹塑性变形阶段时的描述仅考虑了弹性到弹塑性、弹塑性到完全塑性的过渡,对结合面弹塑性变形阶段的描述不详细深入。YUAN等[7]提出了一种基于MB模型的粗糙表面分形弹塑性接触模型的改进模型,进而推导出一种结合面总的接触载荷、总的实际接触面积的求解模型。然而,该模型并未考虑到结合面材料的应变硬化现象,即材料硬度不再是一个恒定值,而是会发生变化。WANG等[8]考虑到弹塑性变形阶段微凸体变形量发生变化影响材料的硬度H发生变化,构建一新的硬度变化函数,研究各变形的临界条件,对3种变形范围进行重新修正,从而提出一种描述结合面单次加载的分形理论模型[8]。硬度作为表征材料弹性、塑性、强度和韧性等力学性能的重要指标,其值的变化与否直接关系到计算的准确性。根据应变硬化准则,随着微凸体变形量的增大、塑性变形程度增大、加工硬化以及位错强化程度增大等,材料的硬度会表现为增大的趋势。
在结合面刚度方面主要有法向刚度模型和切向刚度模型,温淑花等[9]建立了考虑微接触大小分布的域扩展因子影响的接合面法向接触刚度分形模型,并得出相关参数对法向接触刚度的影响规律。李小彭等[10]建立一种考虑摩擦因素的结合面接触刚度分形模型,并研究各影响因素对法向接触刚度的影响。文献[11-15]考虑微凸体弹塑性变形,建立结合面法向接触刚度分形模型,且验证考虑弹塑性变形情况得到的法向接触刚度大于仅考虑弹性和塑性变形的结果。但以上文献均未考虑硬度变化对接触刚度的影响。
本文作者基于上述研究成果,依据分形理论,考虑弹塑性变形的2个阶段及材料硬度的变化特性建立一种新的结合面加载法向接触刚度分形模型,并研究结合面法向接触刚度的影响因素。研究结果为更加科学合理地描述结合面的微观和宏观接触状态,为机械零件表面的接触、摩擦等问题的研究提供理论依据。
1 考虑硬度变化情况下单个微凸体法向接触刚度分形模型
结合面的接触问题可简化为一等效粗糙表面和一刚性平面的接触问题,即结合面上一系列微凸体和刚性平面的接触问题。简化后的接触模型如图1所示。
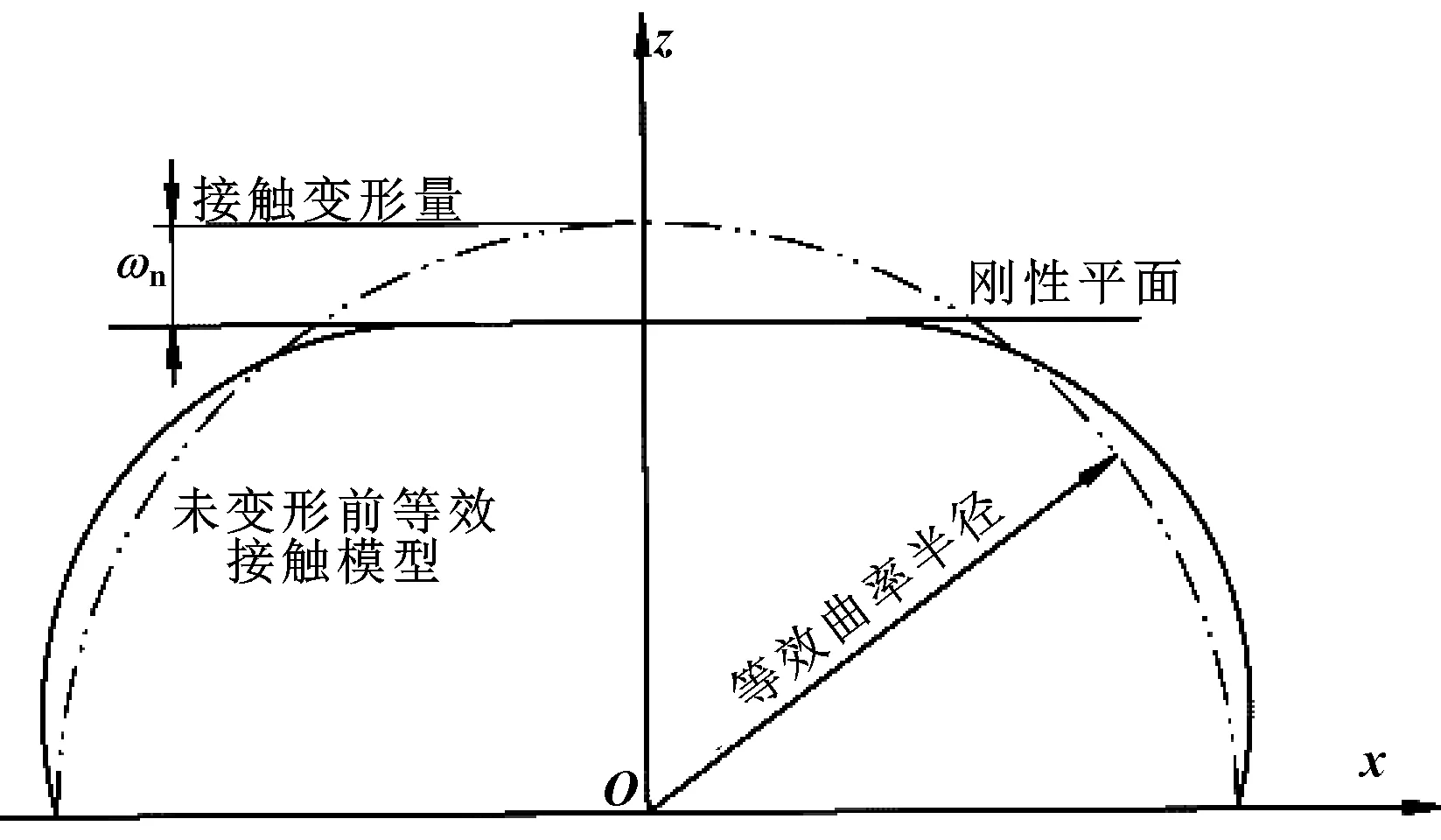
图1 结合面等效接触简化模型示意Fig 1 Simplified model of equivalent contact of joint interfaces
MAJUMDAR等[2-3]研究表明,实际工程粗糙表面形貌的轮廓线具有分形特性,数学特征为处处连续、处处不可微以及具有统计自仿射性,可用Weierstrass-Mandelbort函数(W-M函数)来描述粗糙表面轮廓线,其表达式[15]为
(1)
式中:x为粗糙表面轮廓线函数的横坐标;z为轮廓线的高度;D为Z(x)的分形维数;G是表面的长度尺度参数;nmin是轮廓线对应的最低频率指数;γn是粗糙表面频率密度参数,为适应实际表面轮廓的高频谱密度和相位的随机性,取γ=1.5。
在此做2个假设:①粗糙表面是各向同性的;②不考虑微凸体与微凸体接触过程中的相互作用且认为不会发生大变形。基于该假设可得频率指数为n的微凸体变形前的方程[10]为
(2)
对公式(2)求导可得频率指数为n的微凸体顶端处的曲率半径:
(3)
在微凸体加载过程中,随变形量ωn的增大微凸体将依次由弹性到弹塑性再到完全塑性变形。微凸体在初始屈服时的弹性临界变形[12]为
(4)
根据文献[8]可得微凸体弹性临界接触面积为
(5)
根据文献[16]的研究结果,微凸体实际变形量满足ωn>ωnec时,开始发生弹塑性变形,微凸体弹塑性变形分为2个阶段:1<ωn/ωnec≤6时的第一弹塑性变形阶段和6<ωn/ωnec≤110时的第二弹塑性变形阶段。定义微凸体第一弹塑性临界变形量为第一弹塑性变形阶段开始进入第二弹塑性变形阶段时的实际变形量:ωnepc=6ωnec,对应的真实接触面积为anepc。定义微凸体第二弹塑性临界变形量为第二弹塑性变形阶段进入完全塑性阶段时的实际变形量:ωnpc=110ωnec,对应真实接触面积为anpc。微凸体弹塑性变形阶段接触面积-变形量、接触载荷-变形量之间的关系[16]为
(ωnec<ωn≤6ωnec)
(6)
(6ωnec<ωn≤110ωnec)
(7)
1.1 微凸体处于第一弹塑性变形状态
根据文献[8]的研究结果,考虑到加载过程中材料的硬度变化,为了更加准确地表达弹塑性变形阶段的特性,引入极限平均几何硬度HG(a)这一概念,得出微凸体处于第一弹塑性变形阶段时法向接触载荷[8]为
(8)
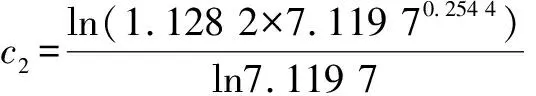
将式(5)代入式(8)得:
(9)
此种情况下单个微凸体的接触刚度为
(10)
1.2 微凸体处于第二弹塑性变形状态
考虑材料硬度变化情况下,微凸体在处于第二弹塑性变形阶段时的法向接触载荷为
(11)
其中,
将式(5)代入式(11)并整理得:
(12)
此种情况下单个微凸体的接触刚度为
(13)
1.3 微凸体处于完全弹性、完全塑形变形接触状态
当微凸体变形量ωn<ωnec时,微凸体处于完全弹性变形阶段。根据赫兹理论,此变形阶段单个微凸体上接触载荷为
此时单个微凸体法向接触刚度为
(14)
当微凸体变形量ωn>110ωnec时,微凸体处于完全塑形变形阶段,在此变形阶段材料的硬度不再受到变形量的影响,认为是一个常量。当材料给定时,微凸体的接触载荷为
fnp=2HπRnωn
此时微凸体的法向接触刚度为
(15)
2 考虑硬度变化情况下结合面实际法向接触刚度
根据文献[5]定义频率指数为n时粗糙表面上微凸体的面积分布密度函数为
(16)
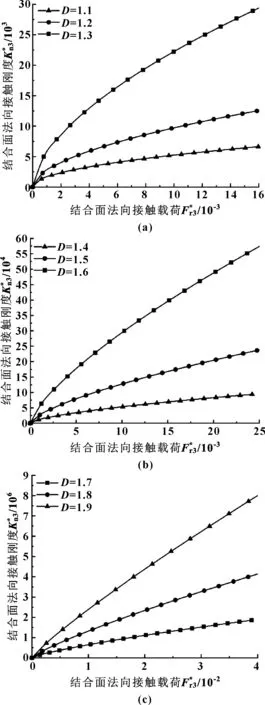
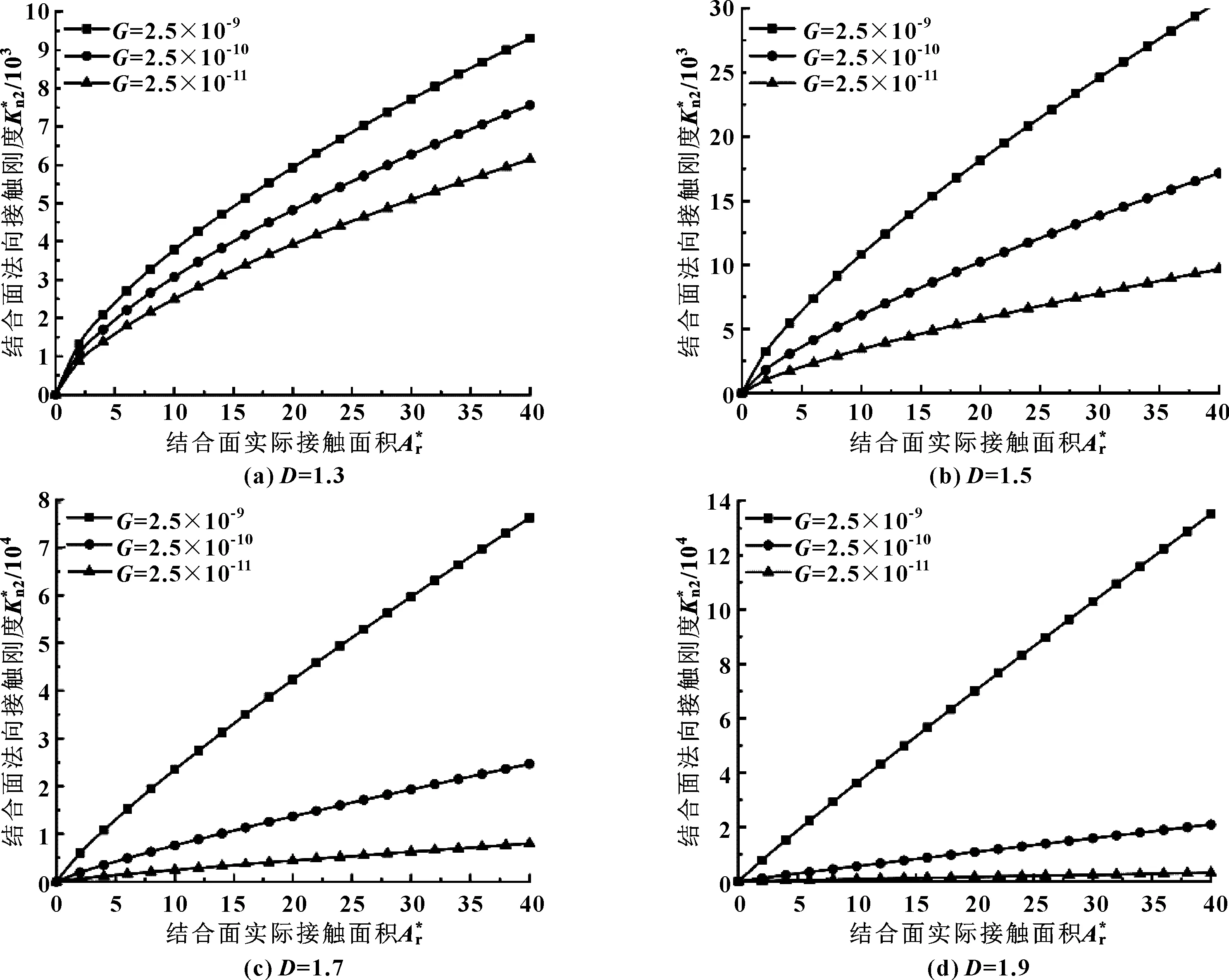
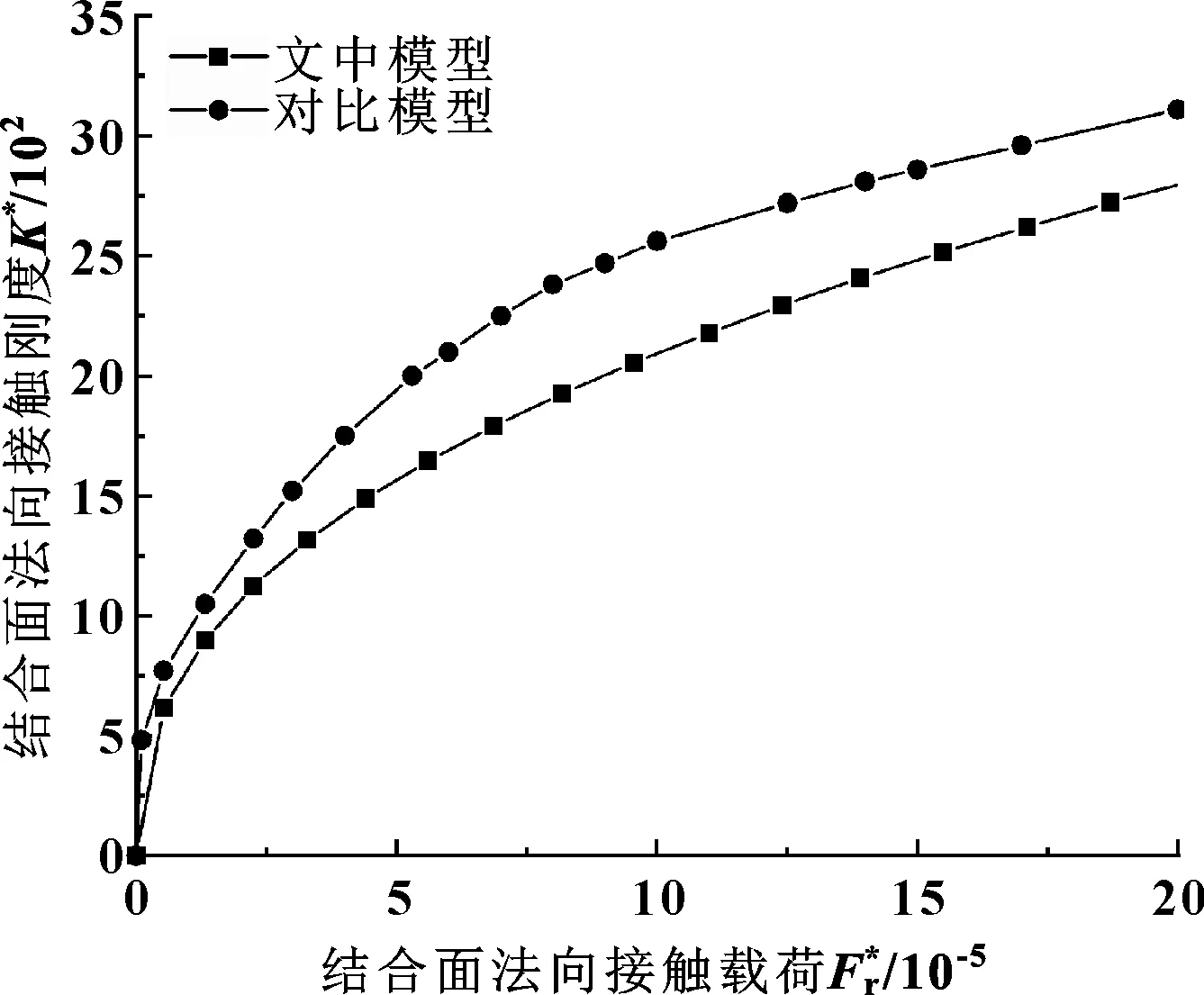
式中:anl是频率指数为n时最大接触点面积。定义nec、nepc、npc分别为弹性临界频率指数、弹塑性临界频率指数、塑性临界频率指数。则在载荷作用下频率指数nmin (1) 当频率指数为nmin 结合面在该阶段的法向接触刚度为 (17) (2)当频率指数为nec 结合面在该阶段的法向接触刚度为 (18) (3)当频率指数为nepc1 结合面在该阶段的法向接触刚度为 (19) 其中, (20) (7.119 7anec)0.872 6(c4+1)-0.5D) (21) (4)当频率指数为npc 结合面在该阶段的法向接触刚度为 (22) 其中, (205.382 70.872 6(c4+1)-D/2-7.119 70.872 6(c4+1)-D/2) (23) (24) 由上可得结合面总的接触刚度为 K=Kn1+Kn2+Kn3+Kn4 (25) (26) (27) (28) (205.382 70.872 6(c4+1)-0.5D-7.119 70.872 6(c4+1)-0.5D)+ (29) 同时可得出频率指数为nec (30) 频率指数为nepc1 (31) 为了更进一步分析以上计算结果,等效结合面的参数取表1所示数值进行仿真分析。 表1 等效结合面参数 图2所示为考虑材料硬度变化时微凸体处于第一弹塑性变形阶段,当频率指数n取34[8]、分形维数D取1.5时单个微凸体实际接触面积和接触刚度之间的关系曲线。可以看出,对于一特定的微凸体而言,当频率指数和分形维数一定时其法向接触刚度随实际接触面积增大而增大。 图3所示为微凸体处于第二弹塑性变形阶段,当频率指数n取38、分形维数D取1.5时单个微凸体实际接触面积和接触刚度之间的关系曲线。 图3 第二弹塑性变形阶段单个微凸体实际接触面积和接触刚度关系曲线(n=38,D=1.5)Fig 3 The relation curve of actual contact area and contactstiffness of a single asperity during the secondelastic-plastic deformation stage (n=38,D=1.5) 由图3可以看出,该变形阶段单个微凸体接触刚度随实际接触面积增大而增大,前期增长较快后期增长较慢,拐点出现在实际接触面积为0.1 m2对应值为6.628×104N/m附近。 图4所示为频率指数为nec 图4 分形维数对关系的影响Fig 4 The influence of fractal dimension on relation 图5 分形维数对关系的影响Fig 5 The influence of fractal dimension on relation 图6 长度尺度参数和分形维数对关系的影响Fig 6 The influence of length scale parameter and fractal dimension on relation(a) D=1.3;(b) D=1.5;(c)D=1.7;(d) D=1.9 图7 长度尺度参数和分形维数对关系的影响Fig 7 The influence of length scale parameter and fractal dimension on relation(a) D=1.3;(b) D=1.5;(c)D=1.7;(d) D=1.9 图曲线对比Fig 8 Contrast of relation curves (1)基于分形理论并考虑结合面第一弹塑性接触、第二弹塑性接触2个弹塑性变形阶段的情形,分别建立考虑硬度变化情况下单个微凸体加载过程中法向接触刚度模型。 (2)考虑加载过程中硬度变化对接触刚度的影响,建立一种新的弹塑性变形阶段结合面法向接触刚度模型。 (3)根据文中给出的模型,单个微凸体法向接触刚度模型与材料属性(等效弹性模量、泊松比、材料初始硬度)、分形参数(分形维数、频率指数、粗糙表面频率密度参数、表面长度尺度参数)以及变形量有关。 (4)弹塑性变形阶段考虑硬度变化时,结合面量纲一法向接触刚度的值随法向实际接触载荷、实际接触面积的增大均增大。实际接触载荷一定时,结合面法向接触刚度值随着分形维数的增大而增大。分形维数一定时,结合面法向接触刚度与表面长度尺度参数有关,随着其值增大而增大。

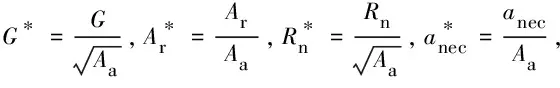
3 结果及分析




4 结论

