活塞偏心倾斜对双筒液压减振器动态阻尼特性影响分析*

郭 鹏 于洋洋 孟祥德 张学玲 张俊红

(1．天津理工大学,天津市先进机电系统设计与智能控制重点实验室 天津 300384；2.天津大学内燃机燃烧学国家重点实验室 天津300072；3.天津大学仁爱学院 天津301636；4.天津捷强动力装备股份有限公司 天津 300410)

被动液压减振器由于工艺成熟，成本适中等特点，在汽车悬架中得到普遍的应用[1]。在不断追求汽车平顺性、舒适性和安全性的要求下，对被动液压减振器减振性能提出了更高要求，其动态阻尼特性对汽车的动态性能有着很大影响[2-3]。随着减振器的长期使用，同时伴随着失效的问题，常见的缺陷有机械损伤、裂纹、体内凹陷、弯曲杆,活塞的破坏、失效和自然磨损等[4]。其中弯曲杆尤为突出，在使用过程中，轻微弯曲，导致活塞倾斜，导致阻尼力过大，对汽车的平顺性、舒适性和安全性造成严重的影响，因此，该问题也成为值得研究的方向。

目前，在研究双筒液压减振器性能的方法中均应用了流体力学理论，且都是基于数学模型的方法。DUYM[5]、YUNG和COLE[6]在对减振器内部结构和运行过程进行详细建模的基础上，提出了物理模型，分析了减振器的减振性能。陈齐平等[7]对减振器的阀系结构进行了分析，获得了减振器复原阀阻尼力特性曲线和内部阀系在不同工况下的压力场特性。BERGER[8]、LION和LOOSE[9]提出了由缓冲器、弹簧和摩擦元件组成的流变模型，分析了减振性能以及结构参数对阻尼特性的影响。朱海燕等[10]研究了某型号双筒液压减振器的动态阻尼特性，通过MTS 减振器综合性能测试示功机实验验证了常温20 ℃下减振器的动态阻尼特性。邹琳等人[11]建立了减振器阻尼力数学模型，研究了活塞杆直径、复原阀片外半径和冲入气体对动态阻尼的影响。李朝峰等[12]建立了局部载荷作用下弹支环形阀片的力学模型，并讨论了阀片变形的影响规律，得到阀片环形受载面积对阻尼力有显著影响的结论。赵立军等[13]提出了液压减振器的油液流量与压降关系的理论分析模型，并建立等效参数化仿真模型，分析液压式馈能减振器外特性和能量回收特性。邓佳林等[14]针对液压减振器故障参数的可测性较差的特点，基于故障诊断技术研究了故障状态下减振器的阻尼特性。孙晓帮等[15]基于能量法研究了减振器的开阀与畸变特性，得到随充气压力的增加减振器抗畸变能力增强的结论。目前对充气式液压减振器的理论研究中大都认为活塞缝隙为环形偏心缝隙，通过缝隙时的流量计算得到阻尼力，但活塞与减振器缸筒之间存在着复杂的动态润滑性能，尤其在活塞杆发生轻微倾斜时，导致活塞偏心和倾斜，活塞与缸筒产生楔形间隙，造成阻尼力的增加，从而影响汽车的舒适性。但目前还没有相关的研究文献考虑此因素求解摩擦阻尼对减振器的影响。因此，有必要考虑活塞偏心和倾斜的流体摩擦因素建立减振器系统的仿真模型，分析减振器活塞偏心和倾斜对减振器动态阻尼特性的影响。

液压减振器的活塞偏心或倾斜对汽车的舒适性能有着严重的影响，本文作者考虑活塞偏心和倾斜与减振器缸筒之间的摩擦与润滑因素，建立双筒式液压减振器的阻尼特性数学模型和动压润滑方程，分析了活塞偏心距比、倾斜角度，活塞倾斜时活塞运动速度、活塞半径、活塞宽度等因素对摩擦阻尼的影响，以及各摩擦因素对减振器动态阻尼特性的影响，为改善活塞偏心和倾斜时减振器动态阻尼特性提供理论参考。

1 分析模型与求解

双筒液压减振器的结构示意图如图 1所示，左右图分别反映了复原行程和压缩行程的工作过程。通过自身的复原与压缩运动，工作缸与储油缸内的油液流过阀系和缝隙，产生阻尼力，衰减振动的能量，从而吸收路面传来的冲击振动。

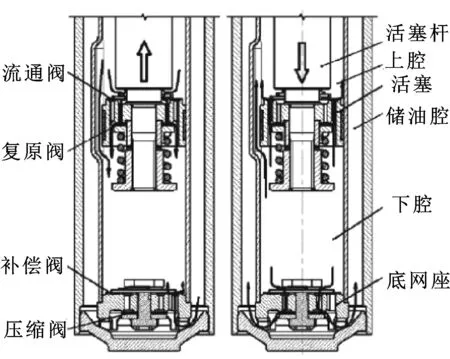
图1 液压减振器结构示意Fig 1 Structure of hydraulic shock absorber

1.1 复原/压缩行程

复原阀开阀前，油液流过常通节流孔和活塞缝隙，常通节流孔流量为QT，活塞缝隙流量为Qxl，其表达式为

(1)

(2)

式中:Cq为常通节流孔的流量系数；AT为常通节流孔的总面积，m2；ρ为油液密度，kg/m3；dh为活塞直径，m；μ为油液动力黏度，Pa·s；Ly为活塞轴向宽度，m；h0为活塞与缸筒之间油膜厚度，m；p1为减振器上腔压力，Pa；p2为减振器下腔压力，Pa。

开阀前油液从上腔室流入下腔室总流量为

Qfh=QT+Qxl

(3)

复原阀打开后，总流量Qfh是经过常通节流孔流量QT与复原阀孔流量Qf的和；其中复原阀孔流量包括复原阀节流孔流量Qfc和环形平面缝隙流量Qff，Qfc和Qff是串联关系即：Qfc=Qff，可得：

(4)

(5)

δrf=frf-frf0

式中:εfc为复原阀节流孔的流量系数；Afc为复原阀常通孔的总面积，m2；rbf为原节流阀片的外半径，m;rkf为复原节流阀片缺口半径，m；δrf为复原阀片的开度，m；frf0为复原阀片的预变形量，m。

油液流过压缩阀常通孔流量Qyc，补偿阀流量Qyb的表达式为

(6)

(7)

式中:εyc为压缩阀常通孔流量系数；Ayc为压缩阀常通孔的总面积，m2；p3为储油腔内的压力，Pa；rbb为补偿阀片的外半径，m；rkb为补偿阀片缺口半径，m；δyb为补偿阀片的开度，m。

阀片的变形量：

(8)

式中：hffp为阀片厚度，m；Grffp为阀片变形系数。

圆环形阀片在任意半径r处的弯曲变形[16]为

Gr=Tc1lnr+Tc2r2lnr+Tc3r2+Tc4+TBr4

阀片变形曲线如图2所示。

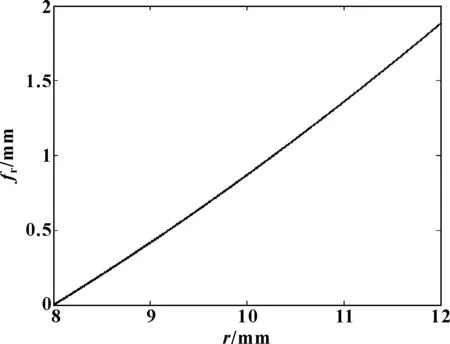
图2 阀片变形曲线Fig 2 Deformation curve of valve plate

开阀后油液从上腔流到下腔总流量为

Qfh=QT+Qf

(9)

油液从下腔流到储油腔总流量为

Qyd=Qyc+Qyb

(10)

储油腔的气体作为理想气体，满足方程：

p3(t)V(t)=p30V0

(11)

V(t)=V0+YAg

(12)

式中：V0为初始体积，m3；p30为初始压力，Pa；V(t)为储油腔内气体的体积，m3；Y为活塞的相对位移，m；Ag为活塞杆截面积，m2。

激励近似认为是正弦激励，作用于减振器得到活塞的相对位移：

(13)

由复原和压缩行程中流经活塞和底阀总成的油液流量与活塞速度之间的关系式(14)，可计算得到减振器上腔压力p1、减振器下腔压力p2和储油腔内的压力p3。

(14)

式中:U为活塞速度，m/s;Ah为活塞截面积，m2；Qyh为压缩行程流经活塞的油液流量，m3。

1.2 减振器活塞/缸筒摩擦副润滑控制方程

减振器活塞/缸筒摩擦分析的平均Reynolds方程[17]表达式如下：

(15)

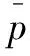
实际油膜厚度h的表达式为

h=h0+hp

(16)

式中:hp为活塞外表面偏心和倾斜时的油膜厚度，m。

考虑活塞偏心和倾斜因素，如图3所示为活塞倾斜的主视图。图4所示活塞倾斜的油膜厚度，活塞倾斜膜厚方程[18]为

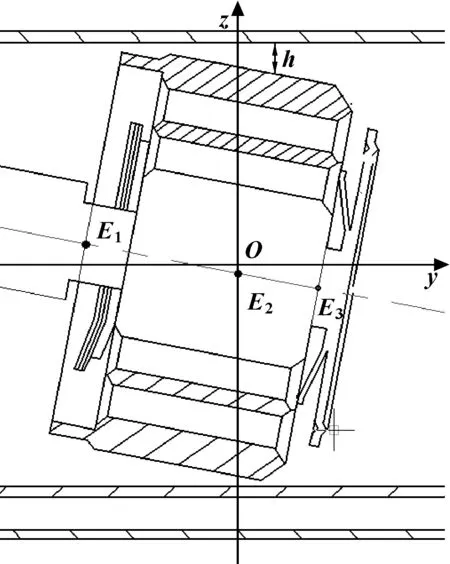
图3 活塞倾斜主视图Fig 3 Front view of piston tilt

(17)

式中：e为活塞中央截面的偏心距，m；θ为始于z轴的角坐标，rad；φ为OE2与z轴的夹角，rad；γ为活塞的倾斜角，rad；β为OE2与E1E3之间的夹角，rad。

1.3 边界条件

减振器活塞/缸筒流场具有收敛的润滑间隙，采用雷诺空化[19]边界条件，p0为标准大气压力，其表达式为

p(x,y=0)=p1，p(x,y=Ly)=p2

p(x=0,y)=p0，p(x=2πR,y)=p0

1.4 控制方程的数值求解

利用五点差分公式对方程(15)离散，活塞周向和轴向划分m×n=125×125个等距网格，坐标系(i,j)表示节点位置，其中 0≤i≤m，0≤j≤n。

采用五点差分法对式(15)进行离散，如图5所示。

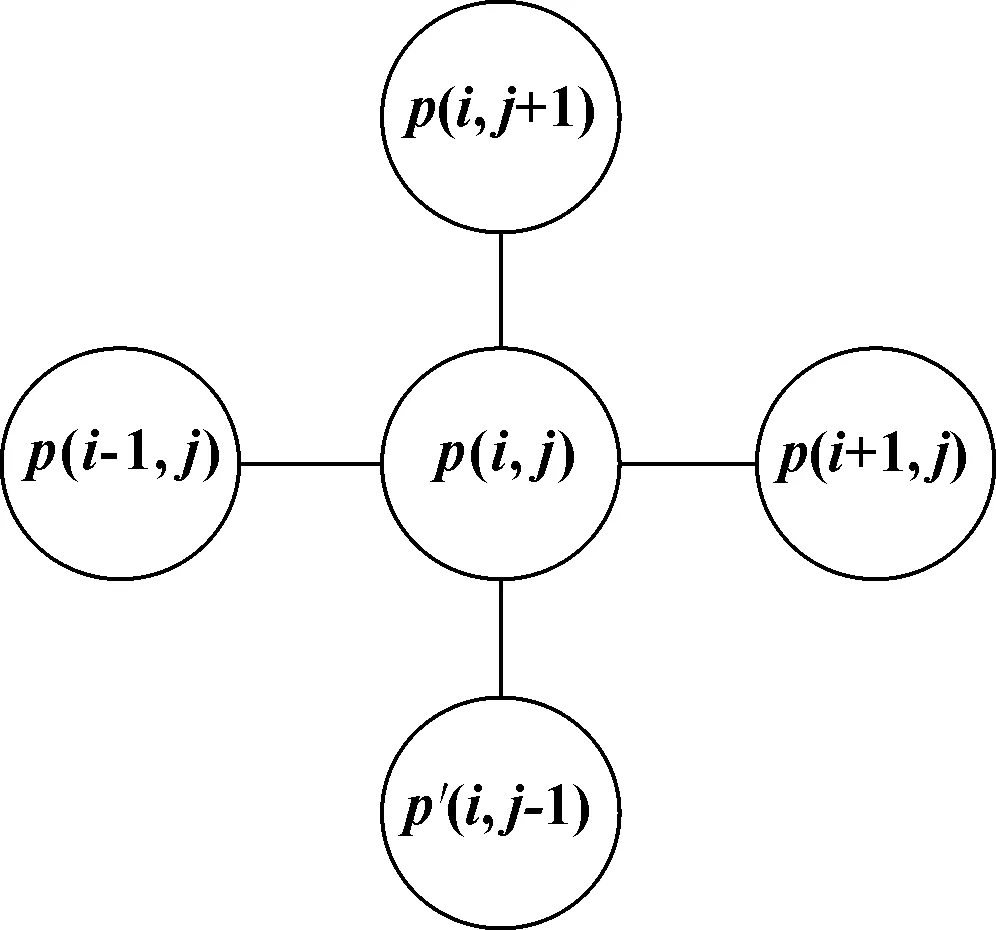
图5 五点差分法关系Fig 5 Relation of five points difference method

差分形式如下：

同理可得：

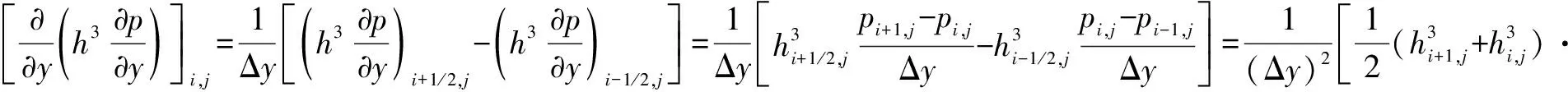
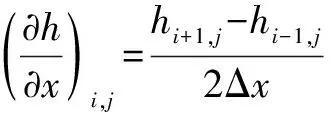
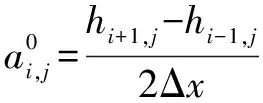
代入式(15)得到离散的Reynolds方程为

(18)

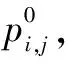
(19)

式中:k为迭代次数;α为超松弛迭代因子。

采用式(20)收敛准则取σ值为10-6进行收敛性判断：

(20)

对油膜压力p在流体域内数值积分，得到活塞表面油膜承载力WN，具体表达式如下：

(21)

活塞表面油膜剪切摩擦力的计算式如下：

(22)

1.5 阻尼力数学模型

减振器的动态阻尼特性主要由阻尼力Ff决定，对活塞进行分析可得到阻尼力的求解公式为

Ff=p1(Ah-Ag)-p2Ah+Ffyou

(23)

式中:Ah为活塞截面积，m2；Ag为活塞杆截面积，m2；Ffyou为油膜剪切摩擦力，N。

阻尼力计算流程如图6所示。

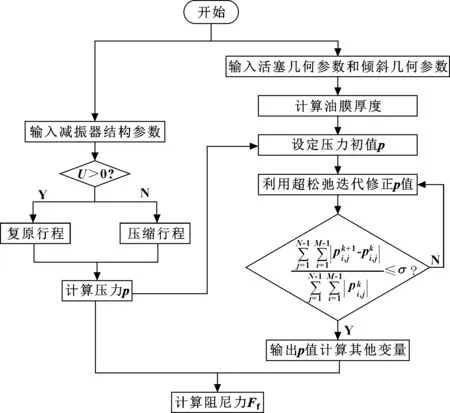
图6 阻尼力计算程序Fig 6 Program of damping force calculation

2 相关参数

减振器相关参数如表1所示，由参数数据仿真可得活塞外表面的压力p分布，如图7所示。

表1 减振器参数

图7所示为利用五点差分法计算的活塞在0.051 rad的倾斜角和0.5h0的偏心距时活塞与缸筒之间的压力p，表面油膜压力和厚度变化趋势基本相同，偏心和倾斜使油膜厚度呈现典型的楔形间隙，厚度h呈现逐渐增加或减小的趋势，使得活塞与缸筒之间产生的压力p较大。

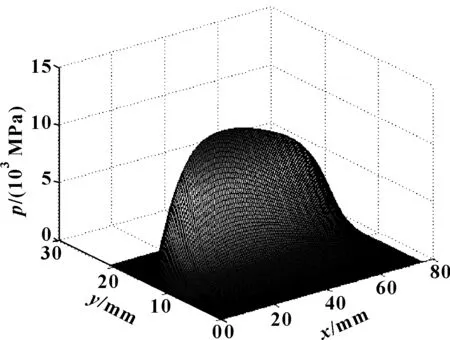
图7 活塞外表面的压力分布Fig 7 Distribution of pressure on the outer surface of piston

3 结果与分析

当活塞存在偏心和小角度倾斜时，影响减振器油膜摩擦力Ffyou和动态阻尼特性的因素有偏心距比ξ=e/h0、活塞倾斜角度γ、活塞半径R、活塞宽度Ly。

3.1 偏心距比对油膜摩擦力和动态阻尼的影响

图8所示为不同活塞速度下活塞倾斜时活塞偏心距比ξ对油膜摩擦力的影响。偏心距比的增加，使得在活塞与缸筒之间的油膜厚度h逐渐减少，楔形间隙逐渐变化，导致活塞外表面压力p增加，利用公式(22)计算可得到活塞与缸筒之间的油膜摩擦力增加。偏心距比ξ在0～0.96之间，随ξ的增加，摩擦力Ffyou增加。ξ在0～0.91之间摩擦力Ffyou呈二次函数形式增加，ξ较小时，增加缓慢，ξ较大时增加较快；当ξ大于0.91时，摩擦力Ffyou呈一次函数形式增加，且斜率较大，增加较快。摩擦力Ffyou随活塞速度U的增加而增加。活塞外表面压力p的增加，导致初始压力p1和p2的增加，以及油膜摩擦力Ffyou的增加，导致示功图面积和阻尼力的增加，如图9所示为活塞倾斜时示功图随活塞偏心距比ξ的变化情况，示功图面积随活塞偏心距比ξ的增加而增加，且ξ越大,面积增加速率越大。图10所示为活塞倾斜时速度特性随ξ的变化情况，可知随ξ的增加，阻尼力增加，且ξ越大,阻尼力增加速率越大。

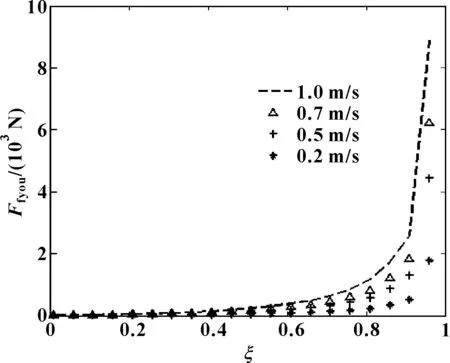
图8 不同活塞速度下摩擦力Ffyou随偏心距比ξ的变化Fig 8 Variation of oil film friction Ffyou with eccentricity ratioξ under different piston speed

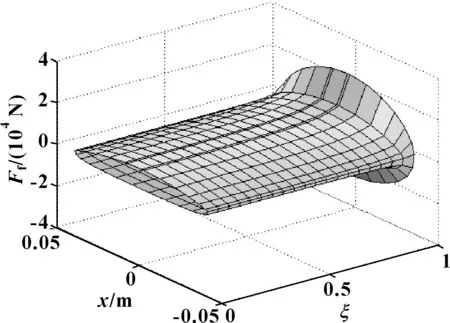
图9 示功图随偏心距比ξ的变化Fig 9 Variation of indicator diagram witheccentricity ratio ξ

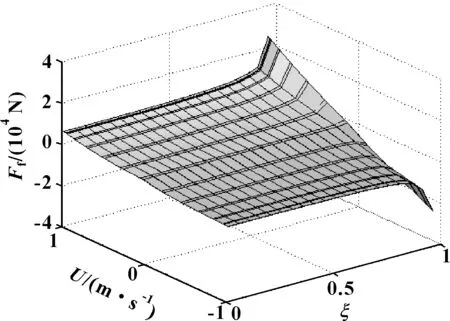
图10 速度特性随偏心距比ξ的变化Fig 10 Variation of characteristic of velocitywith eccentricity ratio ξ

3.2 倾斜角度对油膜摩擦力和动态阻尼的影响

图11所示为不同活塞速度下活塞倾斜角度γ对摩擦力的影响。活塞倾斜角度γ的增加，使得在活塞与缸筒之间的油膜厚度h逐渐减少，楔形间隙逐渐变化，导致活塞外表面压力p增加，利用公式(22)计算可得到活塞与缸筒之间的油膜摩擦力增加。活塞倾斜角度γ在0.005～0.51 rad之间，随γ的增加，摩擦力Ffyou增加，摩擦力Ffyou随活塞速度U的增加而增加。活塞外表面压力p的增加，导致初始压力p1和p2的增加，以及油膜摩擦力Ffyou的增加，导致示功图面积和阻尼力的增加，如图12所示为活塞倾斜时示功图随活塞倾斜角度γ的变化情况，示功图面积随活塞倾斜角度γ的增加而增加，阻尼力也增加。图13所示为活塞倾斜时速度特性随活塞倾斜角度γ的变化情况，可知随活塞倾斜角度γ的增加，阻尼力增加。

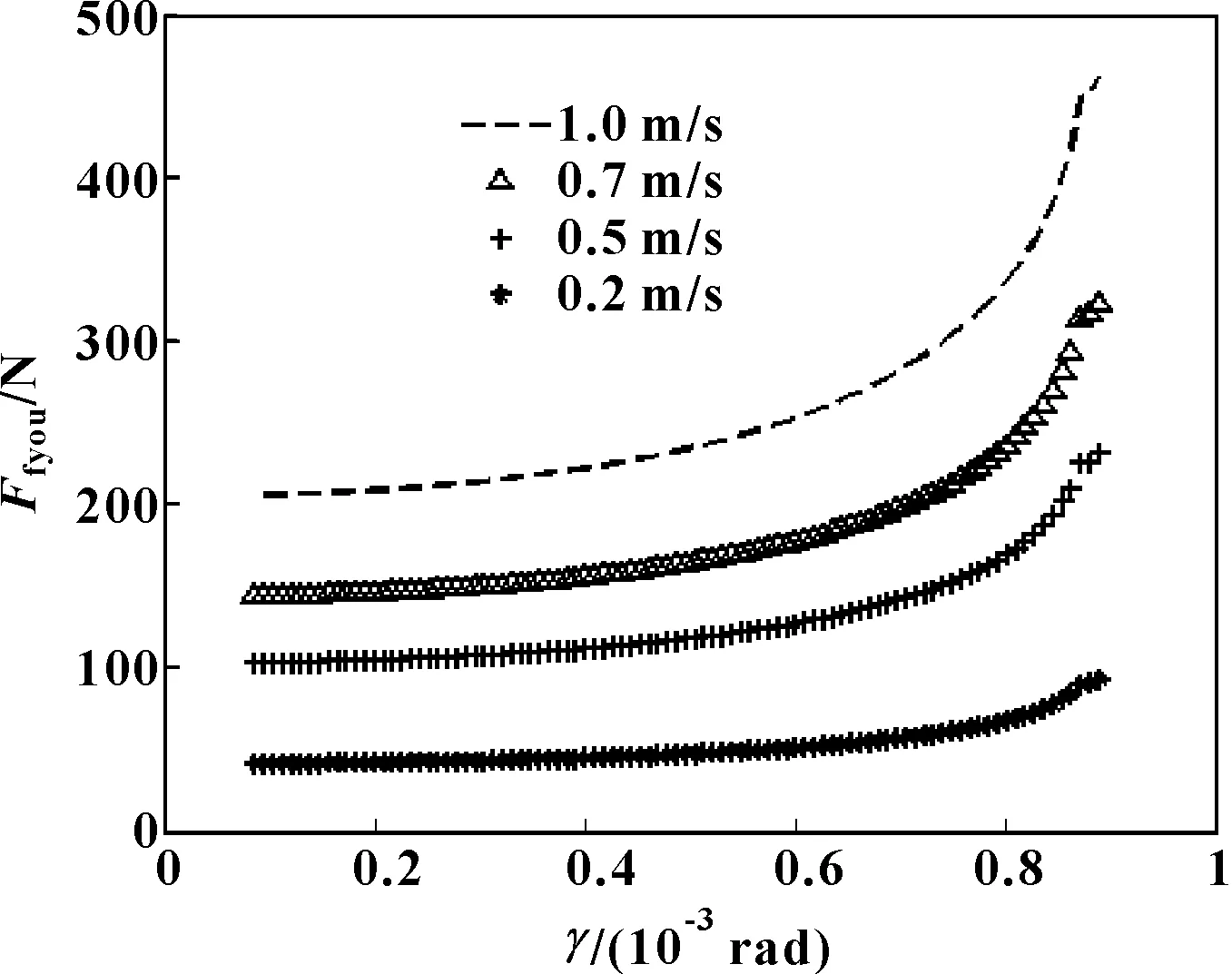
图11 不同活塞速度下摩擦力Ffyou随活塞倾斜角度γ的变化Fig 11 Variation of oil film friction Ffyou with piston inclinationangle γ under different piston speed

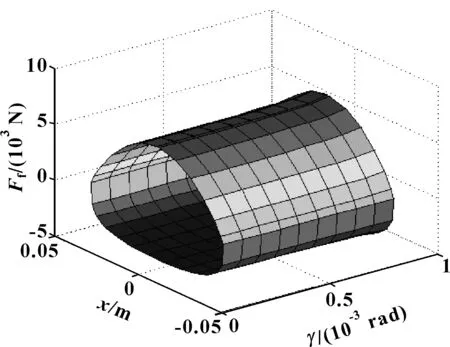
图12 示功图随活塞倾斜角度γ的变化Fig 12 Variation of indicator diagram withpiston inclination angle γ

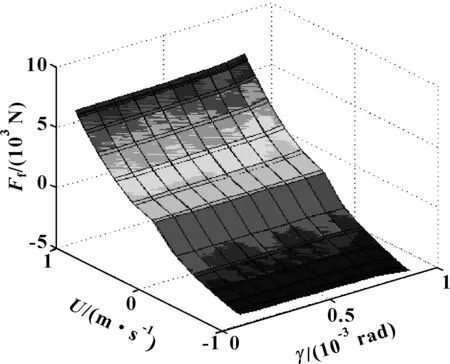
图13 速度特性随活塞倾斜角度γ的变化Fig 13 Variation of characteristic of velocity withpiston inclination angle γ

3.3 活塞半径对油膜摩擦力和动态阻尼的影响

图14所示是不同活塞速度下活塞倾斜时活塞半径R对摩擦力的影响。活塞倾斜时活塞半径R的增加，使得在活塞与缸筒之间的油膜厚度h变化程度减少，导致活塞外表面压力p减小，利用公式(22)计算可得到活塞与缸筒之间的油膜摩擦力减小。活塞半径R在8～30 mm之间，随活塞半径R的增加，摩擦力Ffyou逐渐减小，摩擦力Ffyou随活塞速度U的增加而增加。活塞外表面压力p的减小，导致初始压力p1和p2的减小，以及油膜摩擦力Ffyou的减小，导致示功图面积和阻尼力的减小，如图15所示为活塞倾斜时示功图随活塞半径R的变化情况，活塞半径R在8～18 mm时，截面面积随活塞半径R的增加而增加，复原阻尼力减小，压缩阻尼力增加；活塞半径R在18～30 mm时，截面面积随活塞半径R的增加而减小，阻尼力减小。图16所示为活塞倾斜时速度特性随活塞半径R的变化情况，活塞半径R在8～18 mm时，随活塞半径R的增加，复原阻尼力减小，压缩阻尼力增加；活塞半径R在18～30 nm时，随活塞半径R的增加，阻尼力减小。

图14 不同活塞速度下摩擦力Ffyou随活塞半径R的变化Fig 14 Variation of oil film friction Ffyou with pistonradius R under different piston speed

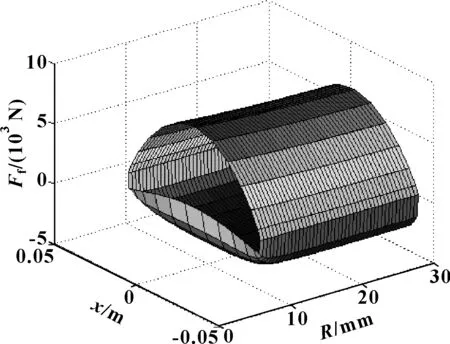
图15 示功图随活塞半径R的变化Fig 15 Variation of indicator diagram with piston radius R

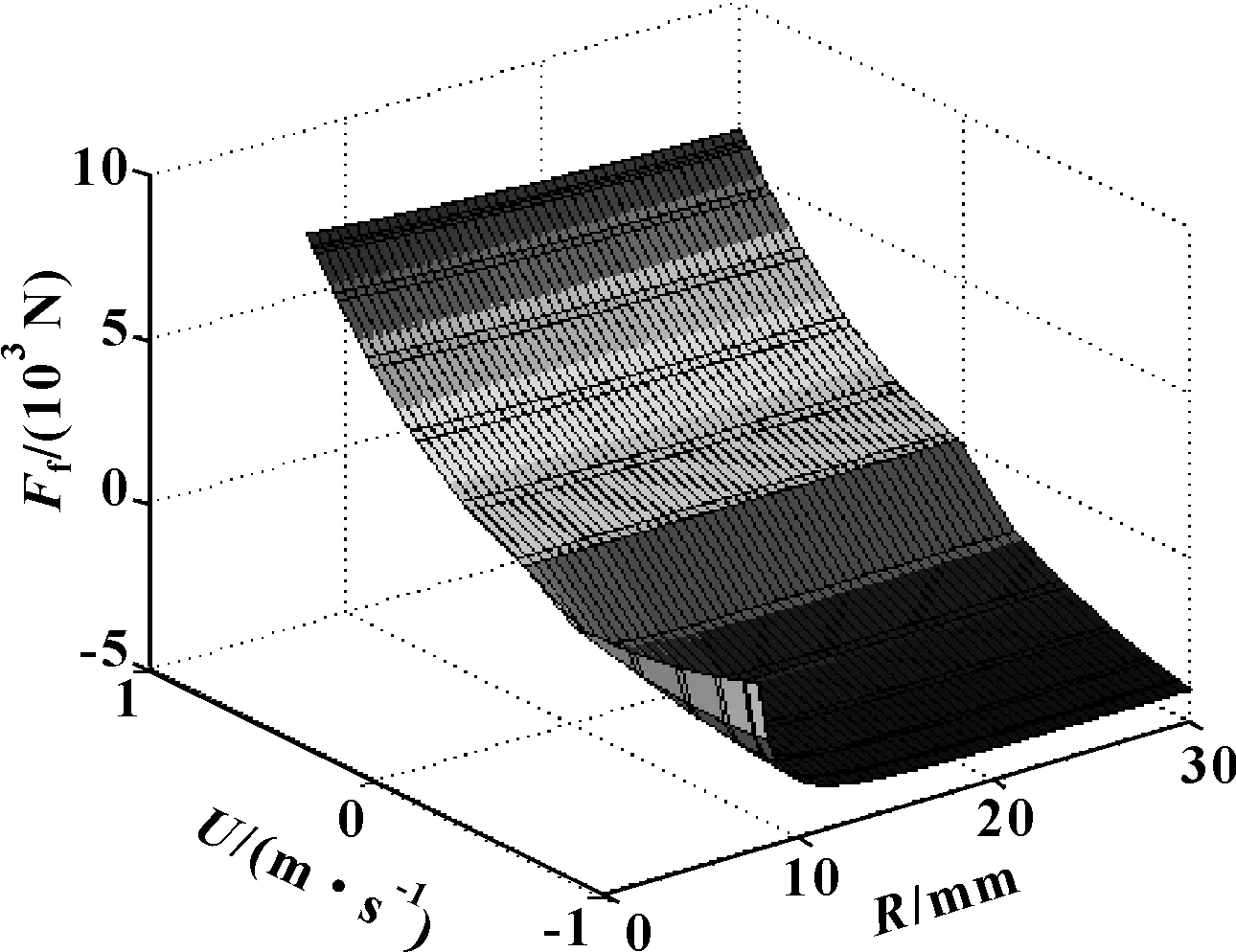
图16 速度特性随活塞半径R的变化Fig 16 Variation of characteristic of velocity with piston radius R

3.4 活塞宽度对油膜摩擦力和动态阻尼的影响

图17所示为不同活塞速度下活塞倾斜时活塞宽度Ly对摩擦力的影响。

图17 不同活塞速度下摩擦力Ffyou随活塞宽度Ly的变化Fig 17 Variation of oil film friction Ffyou with pistonwidth Ly under different piston speed

活塞宽度Ly的增加，使得在活塞与缸筒之间的油膜厚度h的变化区间增加，楔形间隙逐渐变化，导致活塞外表面压力p增加，利用公式(22)计算可得到活塞与缸筒之间的油膜摩擦力增加。织构深度Ly在5.5～20 mm之间，随活塞宽度Ly的增加，摩擦力Ffyou增加，摩擦力Ffyou随活塞速度U的增加而增加。活塞外表面压力p的增加，导致初始压力p1和p2的增加，以及油膜摩擦力Ffyou的增加，导致示功图面积和阻尼力的增加，如图18所示为活塞倾斜时示功图随活塞宽度Ly的变化情况，示功图面积随活塞宽度Ly的增加而增加，阻尼力也增加。图19所示为活塞倾斜时速度特性随活塞宽度Ly的变化情况，随活塞宽度Ly的增加，阻尼力增加。

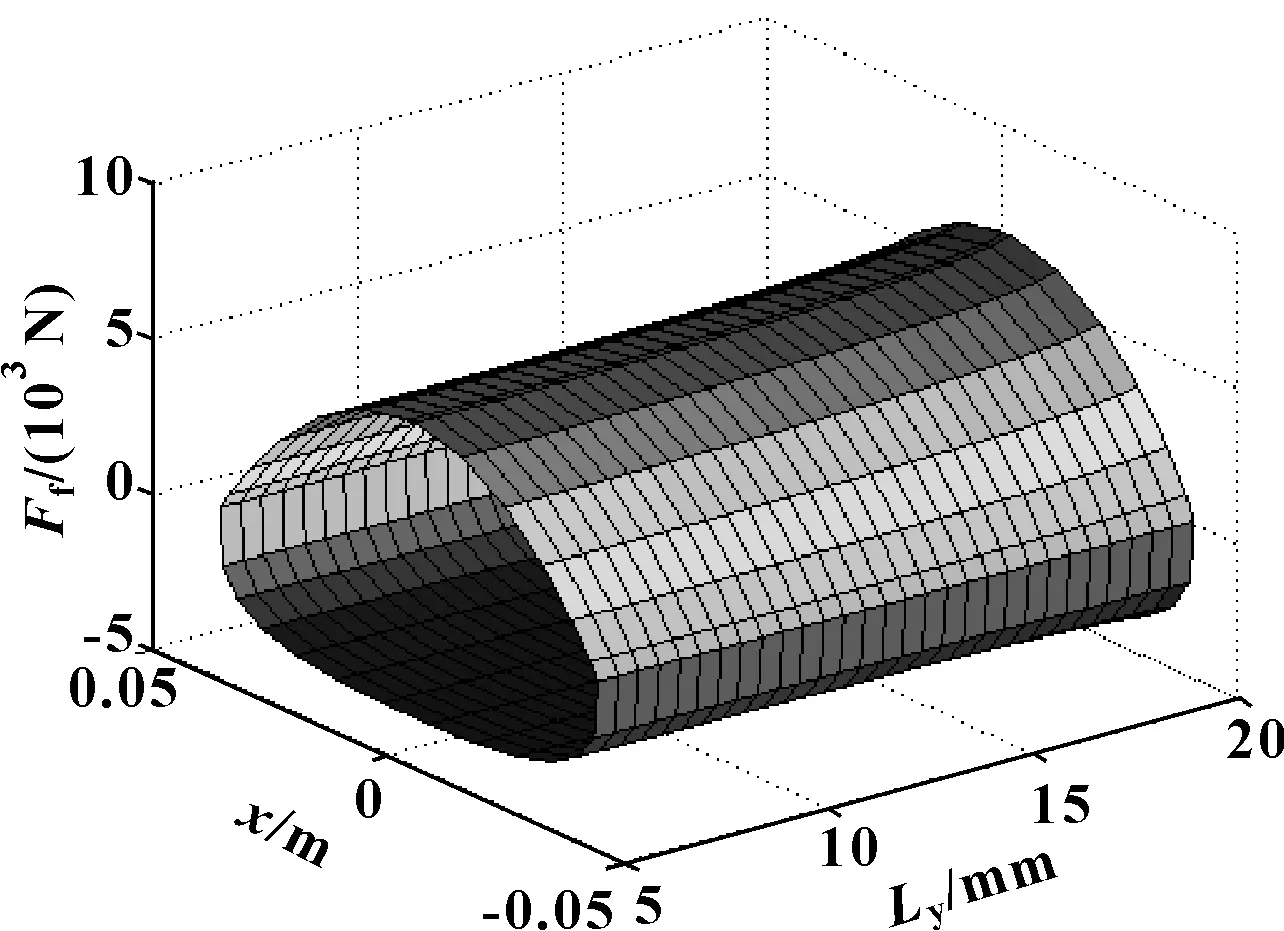
图18 示功图随活塞宽度Ly的变化Fig 18 Variation of indicator diagramwith piston width Ly

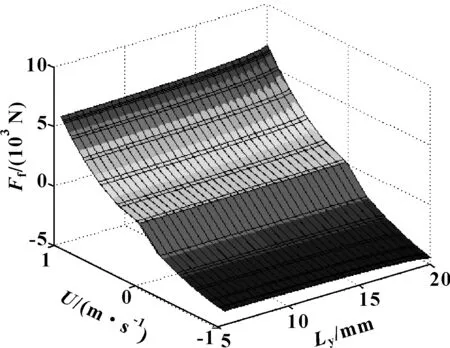
图19 速度特性随活塞宽度Ly的变化Fig 19 Variation of characteristic of velocitywith piston width Ly

3.5 油膜摩擦力对动态阻尼特性的影响

在活塞偏心距比ξ为0.55，活塞倾斜角度γ为0.051 rad，活塞半径R为12 mm，活塞宽度Ly为20.5 mm时，模拟不同活塞位移和不同活塞速度下减振器阻尼特性，结果如图20所示。结果表明，与活塞未偏心和未倾斜相比，由于偏心和倾斜导致初始压力p1和p2的增加，以及油膜摩擦力Ffyou的增加，从而导致减振器的示功图面积增加，功率提高，速度特性曲线斜率增大。如图20(b)所示，减振器活塞发生偏心倾斜时，造成阻尼力的大幅增大，且随着活塞速度增大，活塞发生偏心倾斜时的阻尼力增幅更大。如当活塞以1 m/s的速度运动时，活塞未偏心和倾斜时，计算出复原阻尼力为5 317 N，压缩阻尼力为3 873 N；活塞偏心和倾斜时，计算出复原阻尼力为7 451 N，相比未偏心和倾斜时提高了40.14%，计算出压缩阻尼力为4 897 N，相比未偏心和倾斜时提高了26.44%。如果阻尼力过大，会严重影响行驶的舒适性能。因此，在减振器活塞发生偏心倾斜时会造成阻尼力的大幅增大，严重影响行驶的舒适性能，且速度越快越严重影响舒适性。

4 结论

(1)考虑活塞偏心和倾斜影响，研究活塞与缸筒之间的摩擦阻尼，建立双筒液压减振器阻尼力数学模型，并得到了相应的阻尼力表达式。

(2)活塞倾斜时减振器活塞与缸筒之间的摩擦力Ffyou随活塞速度U的增加而增加，随偏心距比ξ的增加而增加，随活塞倾斜角度γ的增加而增加，随活塞半径R的增加而减小，随活塞宽度Ly的增加而增加。

(3)在减振器活塞发生倾斜时，造成阻尼力的大幅增加，严重影响行驶的舒适性能，且活塞速度越快，对舒适性影响越严重。