基于DNA链置换的赢家通吃神经网络

王 宾李 亚 赵宏伟

(大连大学先进设计与智能计算省部共建教育部重点实验室 大连 116622)

1 引言

随着大数据时代的到来，计算机需要处理大量的数据。虽然当前的电子计算机能较好地处理这些数据，但是在并行计算和存储能力方面也面临着发展的瓶颈，因此设计具有并行性、运算快和大容量的DNA计算机成为必然的趋势。自Adleman[1]解决了哈密顿路径问题以来，DNA计算受到越来越多学者的关注。一些重要的DNA计算技术和计算模型被提出，其中DNA链置换是重要的技术之一。

DNA链置换[2,3]操作简单，具有自主性[4]。目前，DNA链置换已广泛用于生物逻辑电路[5–7]、催化放大器[8]以及DNA编码等领域[9–12]。例如，Seelig等人[13]基于DNA链置换设计了AND,OR和NOT门，这为逻辑电路的发展奠定了基础。Zhang等人[14]实现了一个用于放大信号的电路，包括具有动态特性的前馈级联电路和具有指数增长动态特性的正反馈电路。另外，Lakin等人[15]提出了一个监督学习框架，使用缓冲的DNA链置换网络开发自适应分子电路，该框架扩展了现有的DNA链置换电路架构。Song等人[16]构建了加法、减法和乘法的基本门，基于这些门，描述了如何构建用于计算输入多项式函数的DNA电路。

近年来，DNA链置换用来构造神经网络取得了令人瞩目的成果。例如，Qian等人[17]使用112条DNA链进行级联，设计了一个4神经元的Hopfield联想记忆。然而由于Hopfield联想记忆在实现“猜心术”游戏时，网络规模较大，Genot等人[18]通过赢家通吃(Winner-Take-All,WTA)效应推广到仅含DNA链的电路，缩小了电路并展示只有23条DNA链构造的“猜心术”游戏。紧接着，Shi等人[19]设计了智能的DNA分子系统，可以自动地执行逻辑运算，该系统由一些特定的“DNA神经元”串联组成。之后，Cherry等人[20]通过使用seesaw门，证明基于WTA的DNA神经网络的可以识别手写数字分为多达9类。

本文提出基于DNA链置换实现的WTA神经网络，采用湮灭进行竞争得到最后的结果。由于不需要进行信号的放大和恢复，这不仅减少了DNA链的数量，提高了工作效率，对于实验操作具有重要意义。将神经元实现的逻辑运算AND,NAND和OR级联解决了线性不可分的分类问题。通过与别人结果的对比，证明本文方法的有效性。为了进一步检验神经元级联的可扩展性，本文构建了一个3人表决器。然后，基于DNA链置换实现了科学家的分类。最后通过对比Visual DSD[21]的实验结果，验证了本文的准确率明显高于其他的方法。本文的其余部分安排如下：第2部分介绍Visual DSD和实验结果,第3部分对文章进行总结。

2 应用与仿真

2.1 Visual DSD

Visual DSD是一种编程语言，可以用于实现DNA电路的组装。它的基本组成要素包括Domain,Toeholds和Branch migration。这种语言假设使用的DNA链中不包含任何2级结构，并且可以把某个功能模块封装成一个含有参数的函数模块，从而可以方便地设计大规模的逻辑电路。其中Table选项卡具有输出表格形式的功能，选项卡中的数据可以被保存成为CSV文件或TSV文件。除了将DNA分子编译为化学反应之外，该工具针对模拟器有3种选择，包括Stochastic模拟器、Deterministic模拟器和准时(Just In Time,JIT)模拟器。

本文使用的是Deterministic模拟器，通过时间的推移产生光滑、确定的图像，运行Visual DSD时默认选择的语义模型为default，分子被识别为分支迁移。采用的反应参数如下：泄漏反应的反应速率常数为10–18mol·s–1·L–1，其中toehold的碱基长度为6个，绑定速率常数为3.0×10–13mol·s–1·L–1，释放速率常数为0.1126 s–1。

2.2 逻辑运算的实现

本文通过化学反应来实现逻辑运算。根据输入的逻辑值设置输入的DNA信号浓度。A的输入代表是否存在逻辑值。如果不存在A，则A的逻辑值表示为“0”，将不会产生E。如果存在A，则A的逻辑值表示为“1”,E的最终浓度将由D的初始浓度确定。权重门必须设计成具有相同的结构，该设计是为了使每个门对每组输入产生不同的响应。其中式(1)和式(2)分别表示权重反应的过程。单链B和权重门D执行链置换反应，为下一次求和做准备。逻辑值“1”或“0”用于表示输入链B以及C是否存在。其中D为权重门，箭头右侧E,F为输出，G表示产生的废物链。C与B具有同样的功能，代表输入链

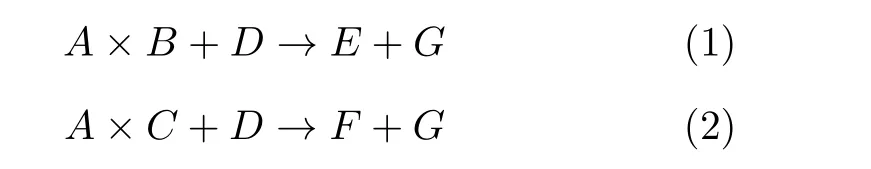
当实现逻辑运算AND时，生成的DNA链E和F相加来实现求和的过程。式(3)为反应公式，L表示权重之和

然后，通过“成对湮灭”进行比较来确定最后的赢家。加入湮灭链(用字母M表示)和帮助链(用字母N表示)，与生成的链L发生反应。其中M限制了输出链的再次生成，同时也促进了竞争反应的发生。式(4)代表反应进行湮灭的过程。在这些过程的基础上，本文实现的神经元结构如图1所示。

图1 神经元结构图

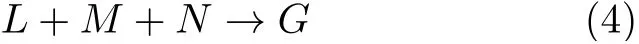
WTA是一种非线性动力学效应，它可以选择性地放大某一个输出。本文将从基于Genot等人[18]实施的电路进行改变，实现的过程如图2所示。从网络形式上来说，本文实现的是前馈网络，前馈相比反馈速度较快，在需要得到一个输出时，输入信号可以被事先推算出来。在网络趋于稳定时，通过最后物种的量显示出结果。这与以反馈形式实现的有所不同[17]，反馈电路会有物种不断生成，然后上一步的输出作为下一次反应的输入。就反应的时间而言，相比带有反馈的电路反应的时间更长，然而本文采用的方法需要的时间则更短。通过控制输入量和M的值来控制反应时间。其次，WTA神经网络不需要添加双轨，这也减少了DNA链的数量，降低了整个网络运行的复杂性。并且WTA神经网络具有普遍的全局效应：一个输出的变化会立即影响所有其他输出的复制速度。

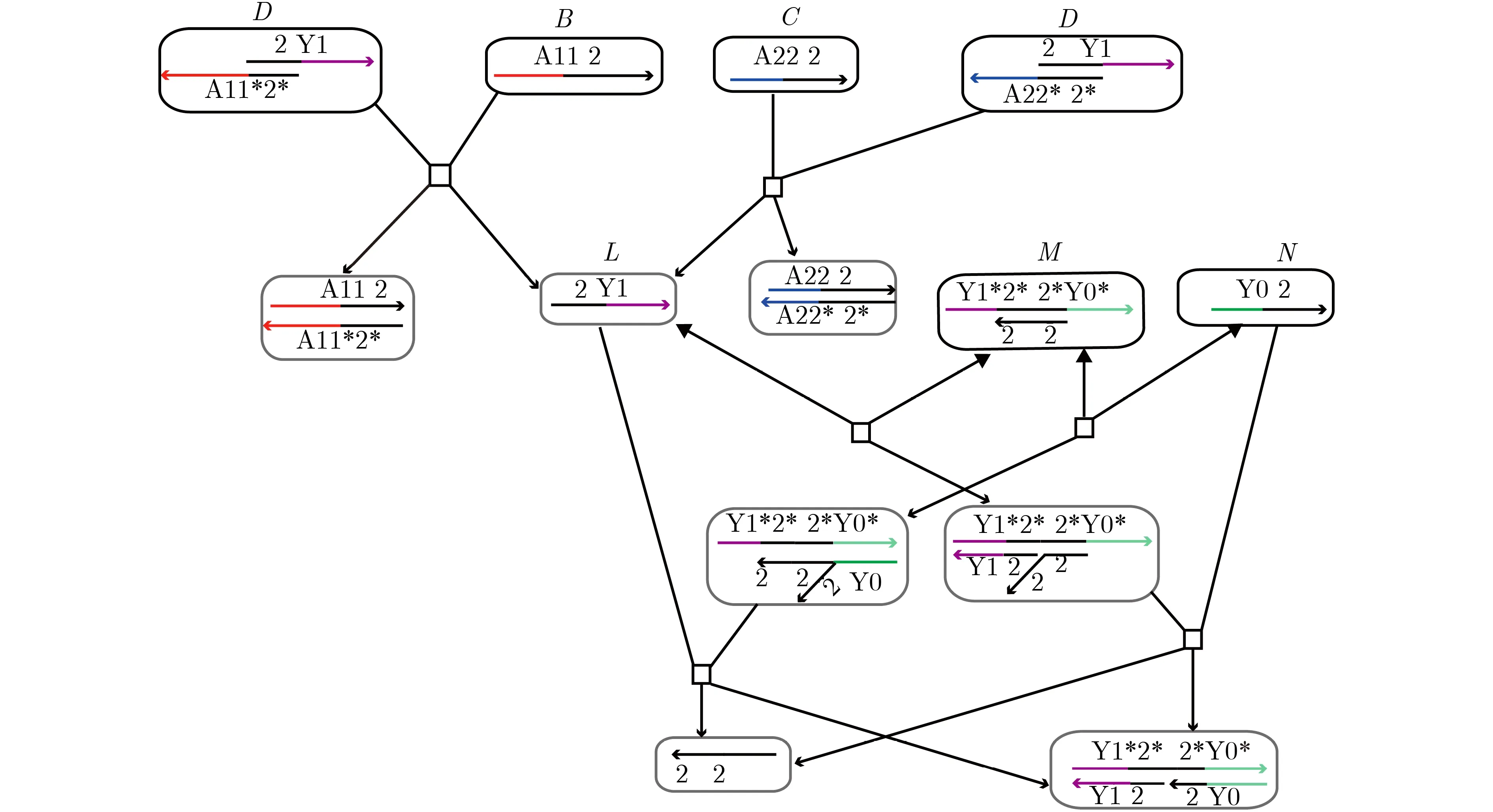
图2 实现AND的过程

首先通过单链,与双链{A11^*}:[2],{A22^*}:[2]发生链置换反应，其中置换出的单链<2 Y1^>是基于DNA链置换的质量作用动力学完成求和操作。最重要的一点是在电路中加入了N单链，与上一步置换出的求和单链<2 Y1^>通过湮灭链[2*2*]发生湮灭反应。当N单链与求和单链<2 Y1^>的竞争趋于稳定状态时，得到最终的结果。WTA神经网络先进行求和，然后DNA链之间进行竞争，这些过程避免了DNA链的再生，使电路容易实现。仿真结果如图3所示，神经元实现逻辑运算AND。图3(b)、图3(c)、图3(d)中单链<2 Y1^>首先呈现出上升趋势，其原因是实现求和的一个过程，然后进一步与加入的N链发生竞争。最后通过DNA链的相互抵消呈下降趋势，当趋于稳定时得到最后的结果。单链<2 Y1^>代表正信号“1”，单链代表负信号“0”。在图3(a)中输入为“00”，图3(b)中输入为“01”，图3(c)中输入为“10”，此时单链变为“on”，表示输出信号为“0”。在图3(d)中输入为“11”，单链<2 Y1^>变为“on”，表示输出信号为“1”。

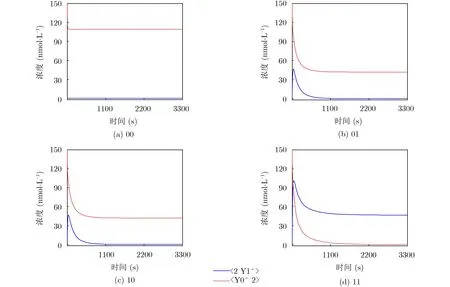
图3 神经元实现逻辑运算AND

通过利用神经元实现逻辑运算NAND，它的仿真结果与AND相反，不同的是在此基础上又增加了一条N链。通过使用神经元实现逻辑运算OR，与AND过程的实现一致，但是需要调整M的值。

单个神经元可以实现单层感知器的功能，即实现线性可分的分类。如逻辑运算AND,NAND和OR能够进行分类。但是，对于线性不可分的问题，这种方法就不是那么方便。因此，在神经元实现逻辑运算AND,NAND和OR的基础上，可以级联形成WTA神经网络，来解决复杂的线性不可分问题。通过WTA将两个相同的输入分为一个类，将另外两个不同的输入分为另一个类，因此应用WTA神经网络可以解决线性不可分问题。在实现逻辑运算XOR时，第1层用神经元实现逻辑运算NAND和OR，其输出作为下一层逻辑运算AND的输入。仿真结果如图4所示。WTA神经网络实现逻辑运算XOR。输出单链<2 Z1^>表示信号“1”，单链表示信号“0”。在图4(a)中输入为“00”，图4(d)中输入为“11”，单链的状态为“on”，表明当输入为相同时，输出信号为“0”。在图4(b)中输入为“01”，图4(c)中输入为“10”，单链<2 Z1^>的状态为“on”，表明当输入不同时，输出信号为“1”。

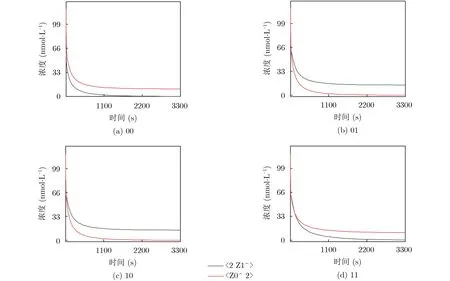
图4 WTA实现XOR的仿真图

在本文中，对比了Wang等人[22]的工作。关于电路的输入，Wang等人[22]采用双轨作为输入，如图5所示。然而我们采用单轨，通过级联神经元构造的逻辑运算AND,NAND和OR来实现XOR，其中WTA神经网络抽象结构如图6所示。其次，双链的结构也有所不同，Wang等人[22]使用带tether的双链，本文利用普通链置换反应的双链。尽管Wang等人[22]实现了对逻辑运算XOR的分类，但是在横坐标中，可以看到它的反应时间较长，相比我们的反应时间更短。因此，本文分析，双轨的加入以及带有tether的双链都是影响最终反应时间的因素。在本文的实验中，NAND的实现不仅解决了NOT门问题，而且避免了双轨，电路结构简单，从而证明本文采用方法的有效性。

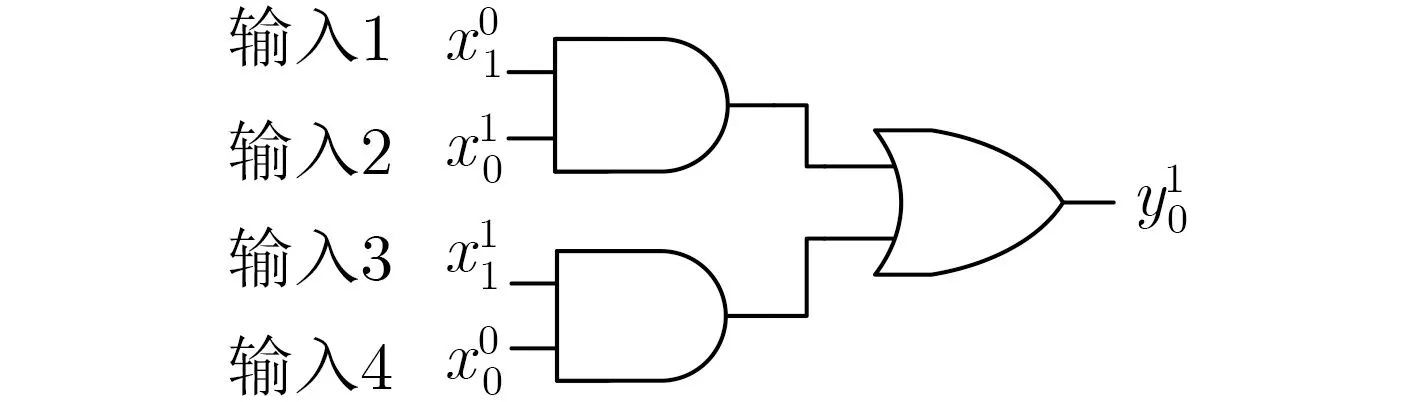
图5 采用AND和OR实现的双轨XOR

图6 WTA神经网络实现XOR

2.3 3人表决器的实现

为了验证神经元级联的可扩展性，本文将电路从单层WTA延伸到多层，设计了一个3人表决器，简化的神经网络结构如图7所示。在这里用字母A,B和C分别表示3位评委，每位评委都有投票权，然后根据投票结果判定是赞成还是反对。如果评委A投票通过，则用逻辑值“1”表示输入。评委B,C没有投票通过，这意味着输入为逻辑值“0”。3位评委A,B和C每个人的投票结果作为输入，字母F表示3位评委最后的投票结果。在3位评委进行投票时遵守少数服从多数的规则，即只有两个或两个以上的评委投票赞成，则代表挑战者挑战成功(输出为“1”)；否则，挑战者将被淘汰(输出为“0”)。3人表决器的仿真结果如图8所示。

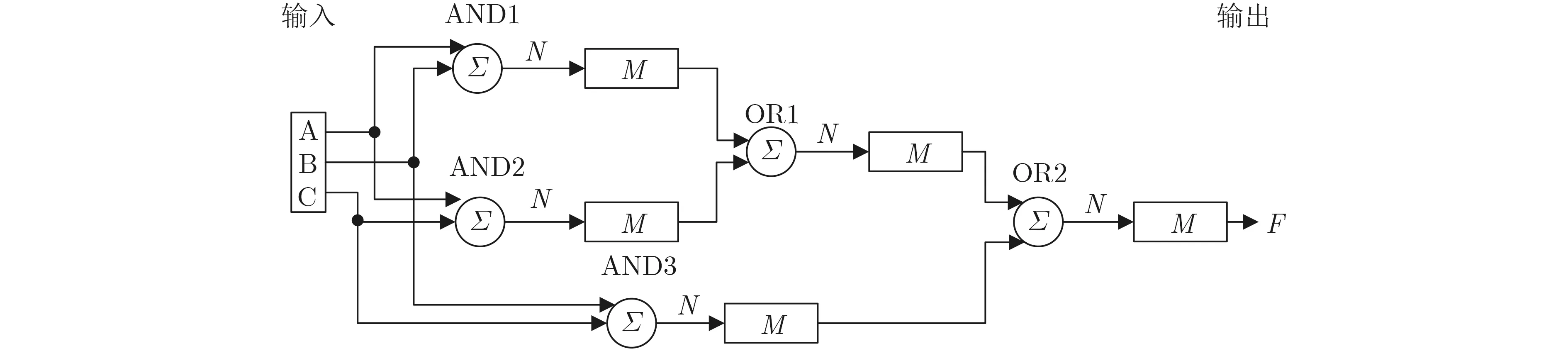
图7 3人表决器的WTA简化结构图

从图8可以看出，图8(d)中输入为“011”，图8(f)中输入为“111”，此时获得的票数为两个或两个以上时，输出为用逻辑值“1”表示，这意味着3位评委均同意，结果表明挑战者挑战成功。如图8(a)中输入为“000”，图8(b)中输入为“001”，图8(c)中输入为“010”，图8(e)中输入为“100”，说明当评委没有进行投票或只有一票时，输出为<2 M0^>用逻辑值“0”表示，表明挑战者以失败而告终。另外，当输入为“101”和“110”时，也会表现出同样的效果。

图8 3人表决器的仿真图

2.4 科学家预测的实现

为了验证WTA神经网络的计算能力，本文实现了对科学家的分类，分类电路的结构如图9所示。图9(a)展示了问题与科学家的对应关系。当肯定回答时，即“1”；当否定回答时，即“0”；当不确定时，显示“?”。图9(b)中，当输入为0011时，可以判断为第3位科学家S3，设计了WTA神经网络的抽象图。图10显示了如何使用与Cherry等人[20]相同的结构来竞争实施WTA神经网络。本文使用前馈电路，上一层的输出发送到下一层，并且每一层之间没有反馈。也就是说，电路上的任何点都将朝该方向前进，并且不会返回到原始点。

图9(a)问题与科学家的对应关系。通过回答问题，每个科学家都拥有一个属于自己的编号，如科学家香农由(0011)表示。图9(b)WTA神经网络抽象图。通过判断输入链X1～X4，直到整个网络响应稳定，判断出最后的获胜者。

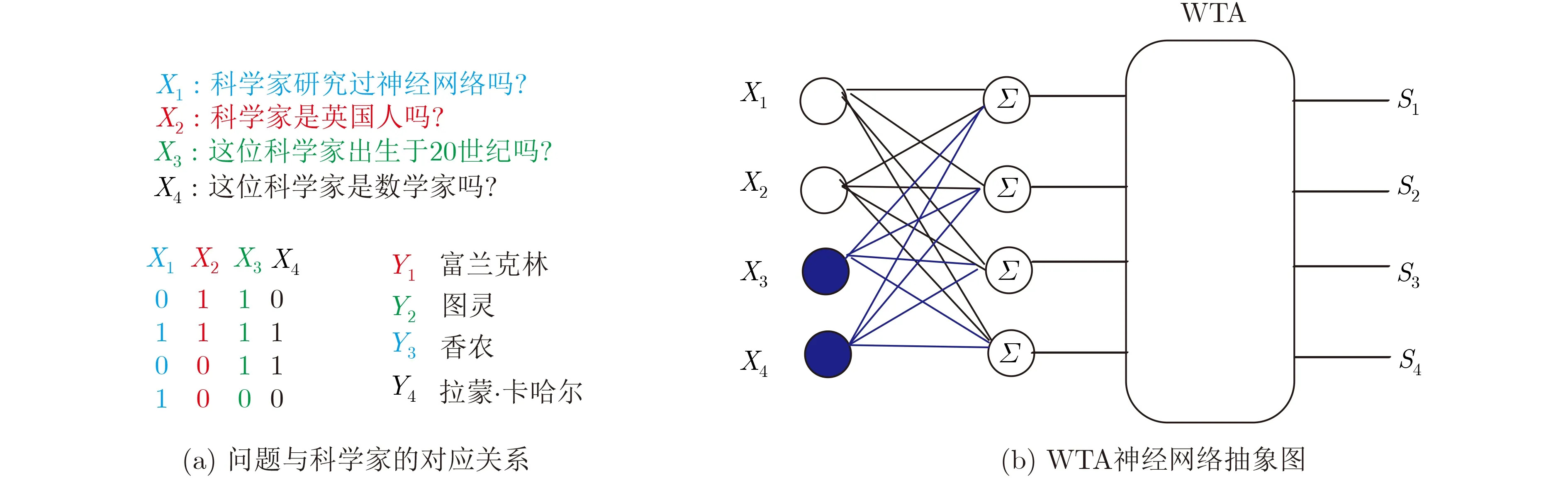
图9 分类电路的结构

这里实现分为3个步骤。首先，在图10(a)中，输入链Xi催化与权重Wij进行反应，并转化成中间产物。为了连续产生输入，下游连接的燃料对双链进行催化。只要有足够的燃料链，输入链就不会受到影响。其次，从图10(b)开始，同一神经元内的所有中间物种与权重发生链置换反应，实现求和Sm。最终，由链置换产生的总和物种彼此之间将相互破坏，直到一个获胜者最终脱颖而出。电路如图10(c)所示。如果仅存在Sm，它将与湮灭发生反应，并且不会消耗任何物种。同样，产物Sn的存在也是仅与湮灭反应，并且不会被消耗。只有当生成的两个物种同时存在时，才显现出湮灭存在的价值。在本文中DNA链之间以湮灭的形式实现，从某一个程度上说，这就是它比Genot等人[18]的方法获得更好结果的原因。基于对不完整信息的“唤醒”，实现了对科学家的分类。输入值采用Qian等人[17]的补充材料图S17a。其中，在网络加权算法和输入链的浓度均与Genot等人[18]的实现一致，通过更改网络结构，输入不完整的信息可以对科学家进行正确分类。

图10(a)释放中间物质。输入链与权重反应生成中间物种，从而为下一步求和创造了条件。燃料链的加入催化生成的双链不断产生输入单链。图10(b)求和。中间物种与双链发生链置换反应以执行求和运算。图10(c)湮灭。所得的求和物种发生成对湮灭反应，最后通过剩余数量确定结果，判别具体的某一位科学家。

图10 WTA神经网络的DNA实现

作为比较，Genot等人[18]实现的电路使用了28条DNA链，本文的输入使用了34条。就链的数量而言，尽管不如Genot等人[18]的简化。但从最终效果来看，Genot等人[18]的14个输入中只有两个可以分类。然而对于同样的输入，在本文中采用的方式能够对其中的13个输入进行正确的分类。通过计算最终完成的任务量，他们的方法仅完成了14%的任务(14个图仅实现2个)。然而通过计算任务完成量，本文达到了92%(14个图实现了13个)。执行的仿真结果如图11所示。因此，湮灭链的选择有很重要的意义，湮灭链的加入使得网络更出色地完成任务。另外，由于缺乏输入信息以及特殊的结构，Qian等人[17]未能对补充材料S17a进行正确的分类。

由图11得知，当图11(b)中输入为???0，被分为第1类；当图11(a)中输入为????、图11(c)中输入为??1?、图11(e)中输入为1???、图11(f)中输入为???1时，被分为第2类；当图11(d)中输入为?0??，被分为第3类；在其他的8种情况中，除了输入?0?0无法识别，网络对其余输入都能够进行分类。[Fuel][0]=1700 nmol·L–1,[N][0]=440 nmol·L–1,[M1][0]=850 nmol·L–1,[M2][0]=3400 nmol·L–1,[M3][0]=1800 nmol·L–1,[M4][0]=1700 nmol·L–1。

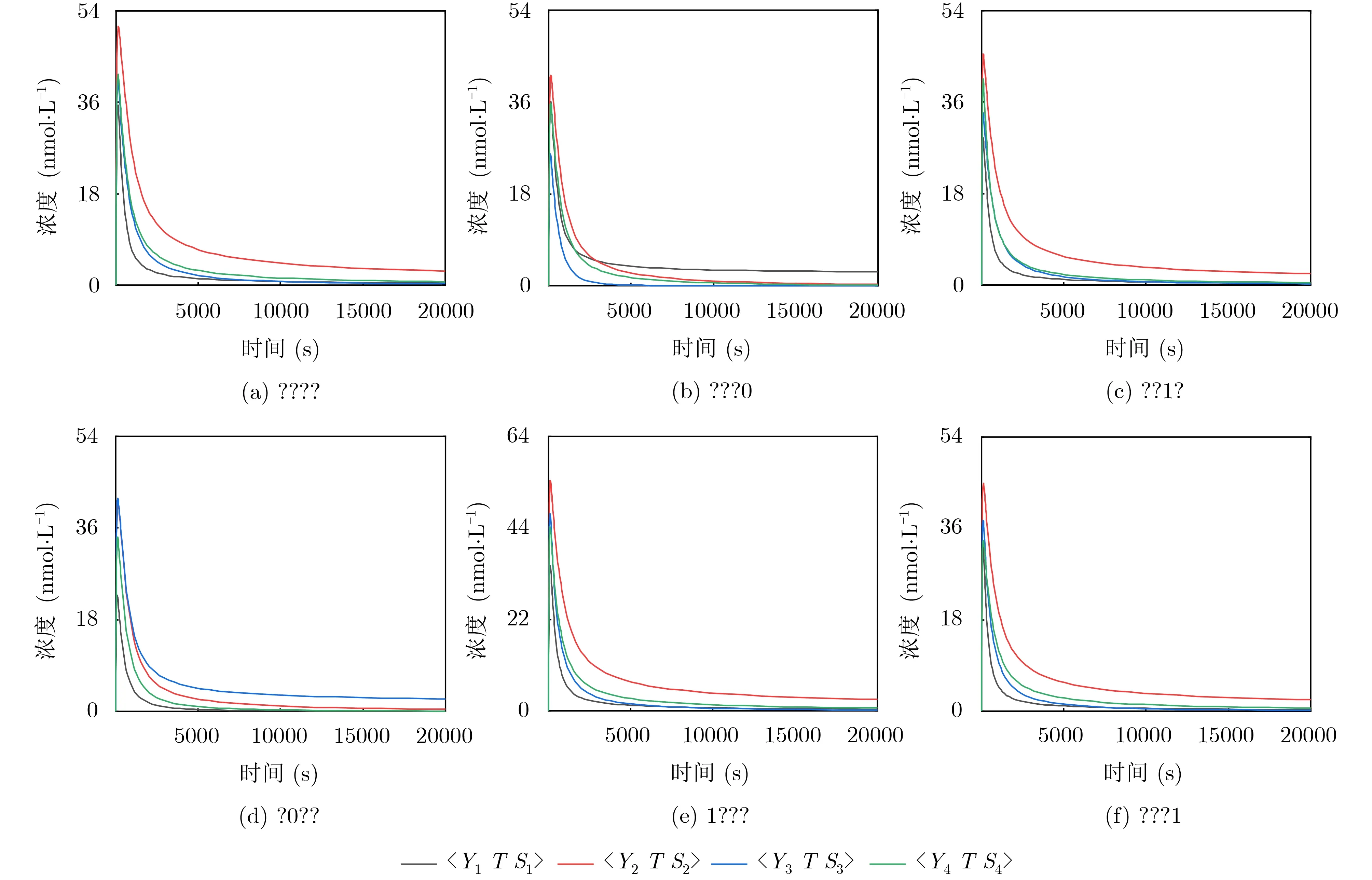
图11 湮灭方法实现科学家模拟图

3 结束语

本文通过对Genot等人[18]实施的“猜心术”游戏的电路进行改变，设计了以神经元形式实现的基本逻辑运算AND,NAND和OR。由于非线性计算成本高昂，所以本文中神经元在执行AND,NAND和OR逻辑运算时，不涉及非线性计算。通过将神经元级联为WTA神经网络完成了复杂的线性不可分问题。另外，为了验证实现神经元级联的可扩展性，创建了一个3人表决器，并在Visual DSD上对电路进行仿真，获得很好的实验结果。然而，为了验证所采用方法的可扩展性，还实现了科学家的分类，并且通过与前人工作的比较证明了该方法的有效性。通过使用DNA链置换电路实现WTA网络时，避免采用双轨作为输入。这不仅减少了DNA链的数量，也降低了网络的复杂度，这样提高了工作效率。

神经网络中权值的设置是处理信息的重要方式之一，但是在DNA生化反应中不断更新权值是不容易实现的。因此本文是采用灌输式学习，将权值设置为固定值，此外这种学习是一次性的。另外，由于采用的浓度都是正值，这种设计的局限性在于不容易处理负值。尽管本文实现的网络规模相对较小,但最后的结果还是能够说明:DNA链置换技术在分子计算领域具有的潜在能力。此外，通过DNA链置换技术构建的神经网络一方面借助可变增益放大器[23]，用于处理模拟输入，从而可以进行更广泛的信号分类任务。另一方面，还可以应用核酸反馈控制[24]，使用发夹的可再生跷跷板结构[25]等。在未来的工作中，提高链利用率和负值的加入，尽可能减少可逆反应，将仍是我们研究的重点。将逻辑运算与神经网络、纳米技术等结合，以构建更复杂的计算，DNA链置换将具有更广阔的前景。