一种通用的时间数字转换器码密度校准信号产生方法及其实现
李海涛 李斌康 田 耕 阮林波 赵 前 吕宗璟
(强脉冲辐射环境模拟与效应国家重点实验室 西安 710024)
1 引言
时间作为物理学中7个基本物理量之一,在物理学的发展中起着至关重要的作用,精确获取研究对象的时间信息具有重要的意义。对时间信息的获取可以由时间数字转换器(Time to Digital Converter, TDC)来实现,TDC将时间间隔转换为二进制数字编码,输出到后端分析得到具体的时间信息。TDC广泛应用在高能物理、导航定位、卫星授时、数字通信、医学成像等众多领域,特别是在高能物理实验中[1,2],TDC获取的时间信息能够间接反映粒子的动量、质量等信息,对鉴别粒子种类、诊断粒子反应过程等有很重要的作用。
TDC有多种实现方法,包括时间间隔扩展法、时间幅度转换法、直接计数法、时钟分相法、游标法、抽头延迟链法和差分延迟链法等;各种方法可以独立使用,也可以配合使用,可以实现从普通精度到高精度、从粗时间到细时间的时间间隔测量。从实现方法上来看,TDC的实现方法可以分为模拟方法和数字方法;从实现平台上看,TDC可以在专用集成电路(Application Specific Integrated Circuit, ASIC)、现场可编程门阵列(Field Programmable Gate Array, FPGA)等平台上实现。ASIC-TDC的测量精度和稳定性更高,但是,ASIC-TDC都是针对某一具体应用设计,不具有普适性,并且开发一款ASIC芯片周期很长;FPGA-TDC具有开发周期短、集成度高、成本低、设计灵活等优点,但是其非线性较差。
随着微电子技术、半导体制造工艺的发展,FPGA-TDC的测量精度、稳定性等同步提高,在FPGA上实现高精度TDC具有重要研究意义。目前,基于FPGA实现的高精度TDC的研究主要集中在几个方面:(1) TDC的实现,基于FPGA内部资源实现高精度TDC,把时间信息转换成二进制编码,通过查找表输出至后端;(2) TDC的自动校准,选择合适的校准方法,校准TDC的码宽(bin size),降低FPGA制造工艺、工作电压、工作温度(Process Voltage Temperature, PVT)等参数对TDC性能的影响;(3)针对TDC内部bin size的不一致性,如何平均化超宽bin,降低测量误差,进一步提高测试精度,单链多次平均测量(Wave Union,Ripple method)、多链单次平均测量等方法可以在已有工艺的基础上,尽可能改善FPGA-TDC的非线性,提高测量精度;(4)其他特殊功能,如动态监测并实时校准TDC的bin size,多通道TDC集成使用,针对特殊要求(如航天等)进行TDC的冗余设计等。
论文主要研究FPGA-TDC的自动校准方法,给出码密度校准方法的误差公式,分析了两种常用码密度校准信号产生方法,提出了一种基于相干采样理论的通用TDC码密度校准方法,通过合理设置TDC主时钟和校准信号之间的频率差,结合输出保持电路,产生校准用的随机信号,确保在码密度校准过程中,随机信号均匀分布在TDC的延时路径上,实现对TDC的逐位(bin-by-bin)校准。
2 TDC校准方法
TDC的常用校准方法主要分为平均校准和逐位校准两种[3–5]。平均校准可以对TDC进行快速校准,但是,得到的只是所有延迟单元抽头的平均延迟时间,无法对TDC中每个延迟单元抽头进行逐位校准,会导致较大的测量误差。逐位校准可以对级联延迟链中每一个延迟单元抽头进行bin-by-bin校准,一般通过码密度方法实现,可以精确标定每个延迟单元抽头的延迟时间。
根据文献[1]研究结果,在使用码密度校准方法校准TDC的码宽时,为了尽可能降低延迟单元的时间误差,需要增加校准次数,增加校准次数就会增加校准时间、增加资源占用量;使用时需要根据TDC指标要求折中考虑。在校准信号和TDC主时钟无关的前提下,认为校准信号是随机信号,标准差和校准次数之间的关系式如式(1)所示,式中,N为校准次数,k为级联链抽头数目,T为TDC主时钟周期,T=5 ns,抽头延时选择码宽的中间值,σi为第i个延迟单元的标准差,στ为校准误差最大值。根据式(1),已知文章实现的校准次数为1000000次,对应TDC的校准误差最大值小于5 ps;同理,如果校准次数达到100000000次,对应TDC的校准误差最大值小于0.5ps。从另一个角度分析,如果以5 ps步进延时对TDC进行校准,那么1000000次校准,总步进时间为5 μs,相当于对5 ns周期的时钟遍历1000次,且遍历点不重复。
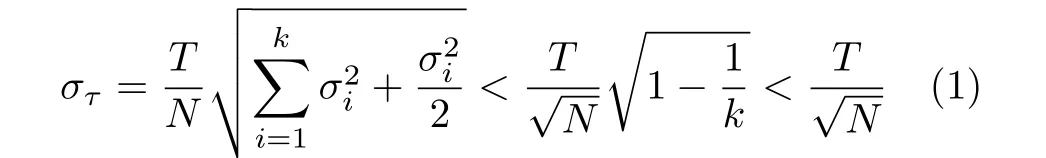
校准信号产生:在游标法实现的TDC中,给出了一种典型的起振电路,该电路利用了FPGA内部的寄存器和门电路等资源,构造了可控的数字振荡电路如图1所示[2],当复位为‘0’,脉冲为‘0’时,电路输出为‘0’,处于稳定状态;当复位为‘0’,脉冲发生0–1跳变时,系统开始起振,电路输出为周期振荡波形,处于振荡状态,震荡周期值为门电路总延时;当复位发生0–1跳变时,振荡状态结束,电路输出为‘0’,回到稳定状态。这种电路结构简单,门电路的延时一般在亚纳秒量级,可以产生高频的振荡信号,通过改变信号的传输链路可以调节振荡频率;缺点是产生的振荡信号受外界因素干扰明显、振荡频率不稳定且抖动较大。一般来说,码密度校准方法的校准次数较多,在一定程度上可以通过平均的方法降低这种抖动的影响。

图1 门控数字震荡电路
文献[1]给出了一种利用FPGA内部的查找表(Look-Up Table,LUT)资源,通过级联查找表建立环形振荡电路的方法。环形振荡电路一般由奇数个反相器级联而成,将最后一个反相器输出反馈到第一个反相器输入可以形成环形结构,达到振荡的目的。FPGA是基于查找表结构建立,拥有大量查找表资源且方便级联,可以通过配置查找表来实现反相器的功能[6]。由查找表LUT 1,LUT2构成的环形振荡器如图2所示,总共包含一个LUT 2和偶数个LUT1,LUT1,LUT2的真值表如表1,表2所示,通过配置LUT 2内部存储值为“0010”,当EN为‘0’时,LUT2不受I0影响,输出始终为‘0’;当EN为‘1’时,LUT 2的输出O与输入I0反向,实现反相器功能;通过配置LUT 1的内部存储值为“10”,实现反相器的功能。在校准过程中,EN为‘1’时,由查找表LUT 1与LUT 2组成的环形结构,相当于奇数个反相器组成的环形振荡电路;在测量或者待机时,为降低功耗、降低干扰,EN为‘0’,由查找表LUT 1与LUT 2组成的环形结构,相当于偶数个反相器,不形成振荡。

表1 LUT1真值表
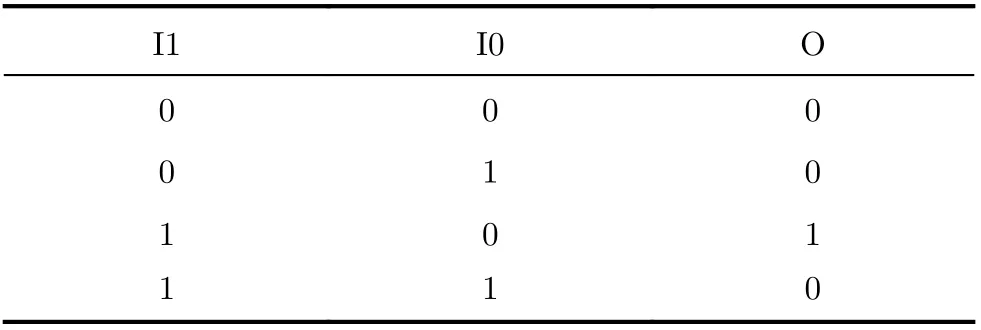
表2 LUT2真值表

图2 利用查找表构成环形振荡器
3 一种新的校准信号产生方法
前述的输出振荡信号作为校准信号的方法,采用FPGA内部的组合逻辑资源,基于自激振荡原理产生可控周期振荡,一般认为产生的校准信号与TDC主时钟无关,是随机信号。在码密度校准过程中,如果校准次数足够多,认为随机信号近似均匀分布在TDC的延时路径上,可以实现对TDC的高精度校准。
TDC的码密度测试与ADC的码密度测试原理类似,区别在于ADC的码密度测试是对幅值随机的模拟信号进行量化统计分析,以标定ADC的输出数字编码的非线性;TDC的码密度测试是对时间随机的数字信号进行量化统计分析,以标定TDC的延迟单元的非线性。在对ADC进行动态性能分析时,需要对正弦波采样数据进行傅里叶分析,如果ADC采样时钟和待采样正弦波频率满足严格的相干采样条件,那么在进行傅里叶分析时,采样信号的频谱就不会出现泄漏现象;否则,采样信号的频谱会泄漏,主要原因之一就是ADC采样的正弦波数据是非相干的,采样数据点有重复。理论上相干采样可以保证ADC采样的正弦波数据之间没有重复的,如果采样数据量足够大,相干采样可以保证采样数据点等效在一个正弦波波形上均匀分布。实际上这种理想条件很难实现,只是近似成立,因为采样时钟频率、正弦波频率本身也有功率谱密度分布,并不是固定在一个频率值上。
对ADC动态性能测试而言,相干采样条件如式(2),fs是采样频率,fin是待采样正弦波频率,M是采样周期数,NFFT是采样点数。相干采样条件要求M和NFFT为整数,且互为素数,并且NFFT为2的整数次幂,可以将该条件等价为:NFFT为2的整数次幂,M为奇数或素数。

从相干采样的角度分析TDC的码密度校准信号产生,借鉴ADC动态性能测试中的相干采样,研究TDC主时钟和校准信号的相干采样问题。对TDC码密度校准而言,可以根据要求对相干采样公式进行优化,如式(3)所示,fTDC为TDC的主时钟频率,fcal为校准信号频率,M,Ncal为整数且互为素数,Ncal不要求是2的整数次幂,NFFT为2的整数次幂是傅里叶分析的要求,Ncal无此项要求。在满足相干采样且校准次数足够多的情况下,可以保证校准信号均匀分布在TDC的延迟链上。
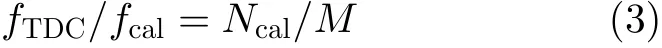
如果式(3)的fTDC,fcal两者的频率值非常接近,M,Ncal非常接近,Ncal/M的值接近于1。以fTDC作为基准,此处研究fTDC稍大于fcal的情况,fTDC–Δf =fcal,TTDC+Δt=Tcal,Δf,Δt都很小,在频域上表现为频率差值Δf,在时域上表现为时间间隔Δt,以fTDC作为基准计算得到Δt如式(4)所示,fTDC稍小于fcal的情况同上述分析。
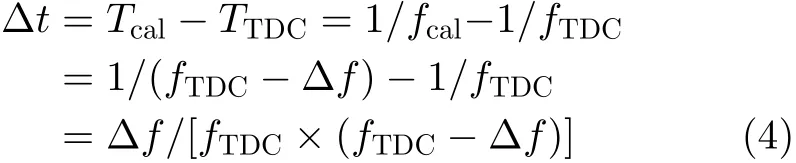
当fcal,fTDC值相差比较小时,以上时间差可近似为Δf/(fTDC×fTDC);当fTDC值为200 MHz时,对应TTDC值为5 ns,如果要求TDC延迟链等效每隔10 ps就校准一次,那么对应的Tcal值为5.010 ns,求出对应的fcal值约为199.6 MHz。实际上,并非每个TDC主时钟周期都完成一次校准。假设每5个TDC主时钟周期完成一次校准(其它要求不变),那么,对应的Tcal值为5.002 ns,求出对应的fcal值约为199.92 MHz时,经过5个TDC主时钟周期,两者相差10 ps。在FPGA上容易实现以上的频率值,fTDC可以直接由外部时钟源直接提供,上述计算得到的fcal频率值可以利用FPGA内部的混合模式时钟管理模块(Mixed-Mode Clock Management,MMCM)资源产生,这种情况下,fTDC和fcal采用同一个时钟源,经过FPGA内部的MMCM产生校准信号,FPGA内部的MMCM资源输出附加的时钟抖动一般100 ps左右,单次校准会增加TDC的时间误差,同第2节描述,多次校准可以把这种时间误差平均化,最终实现对TDC延迟链的校准。
另外一种情况是直接采用两个标称频率值相同的时钟源,分别作为fTDC和fcal的时钟源,理论上两个时钟源的功率谱密度分布不完全相同,两个时钟源不可能输出完全相同频率值,两者之间有很小的频率差,可以认为是相干采样。前文已述,经过MMCM之后的输出会加入额外的时钟抖动,因此可以把时钟信号从专用引脚输入,直接作为TDC的主时钟、校准信号,可以降低传播链路上的抖动。
在码密度校准时,如果校准信号频率过高且直接进入到延迟链中,可能会造成TDC输出编码错误,这就需要对校准信号进行输出保持,以达到以下目的:(1)确保校准过程中TDC的输出编码的有效性;(2)定义经过输出保持后的信号为随机信号,认为随机信号和TDC主时钟无关。一种典型的输出保持电路结构如图3所示,D触发器输入端置‘1’,把校准信号作为D触发器的时钟信号,校准信号的上升沿开始一次随机过程,一次测量结束后对D触发器进行复位清零,等待校准信号的下一个上升沿再次输出高电平。由于校准信号与TDC主时钟满足相干采样条件,又经过了一级输出保持电路,输出的随机信号满足码密度校准要求,可以根据式(1)计算校准误差最大值。

图3 典型的输出保持电路
4 实现及测试
在Xilinx公司28 nm工艺的Kintex-7 FPGA上,采用级联进位链的方法设计实现plain TDC,共使用进位链资源128个,抽头数量256个,精细时间测量范围大于5 ns。论文设计的校准电路结构如图4所示。校准电路模块主要由校准信号产生及保持部分、校准控制部分构成,校准输出的二进制编码结果进入微分统计表、积分查找表(建表)等。校准信号经过保持电路之后认为是随机信号,其产生及保持受校准控制部分控制,随机信号进入到由级联进位链构成的TDC中,精细时间测量结果通过二进制编码输出到建表部分;校准控制起到控制校准使能、控制校准次数、控制建表查询输出等作用;把每次获得的校准结果编码送入微分统计表,根据微分统计表的结果建立积分查找表。在TDC测试时,输出对应的二进制编码至后端分析得到具体的时间信息。

图4 码密度法校准TDC码宽示意
基于相干采样理论,采用两个独立时钟源分别作为fTDC和fcal的时钟源,从专用时钟引脚输入,经过MMCM之后,输出作为TDC的主时钟、校准信号,对进位链plain TDC进行码密度校准。Kintex-7上的单个进位链一般可以输出4个抽头数据,分别是CO0~CO3,经过码密度校准,典型的4抽头的码宽如图5(a)所示,可见抽头码宽并不均匀,与文献[4]中90 nm工艺的Virtex-4 FPGA的进位链抽头码宽类似,Virtex-4进位链抽头码宽示意图如图5(b)所示。对比两者,可见制造工艺的改进的确降低了进位链抽头码宽,但是,对进位链抽头码宽的不均匀性改善不大。

图5 Kintex-7进位链4抽头码宽典型值
结合文献[7–9]的建议,从一个进位链引出两个抽头,将其分割为2个基本延时单元,分别是“CO0+CO3”和“CO1+CO3”两种抽头方式,对应简写为“0tap+3tap”和“1tap+3tap”,研究了两种抽头方式对TDC分辨率和非线性的影响,结果如图6所示,采用“CO0+CO3”的2抽头方式,可以在TDC的分辨率和非线性之间取得较好的均衡。图6显示,每间隔100个码址会出现一个超宽码,这是因为一个时钟区域内只有50个上下级联的进位链,每个进位链引出2个抽头,共100个抽头,之后进位链就需要跨时钟域,不同时钟域会导致超宽码的产生。本文进位链抽头起始位置并不是时钟区域的最底部,所以超宽码出现在94,95,193,194抽头处。
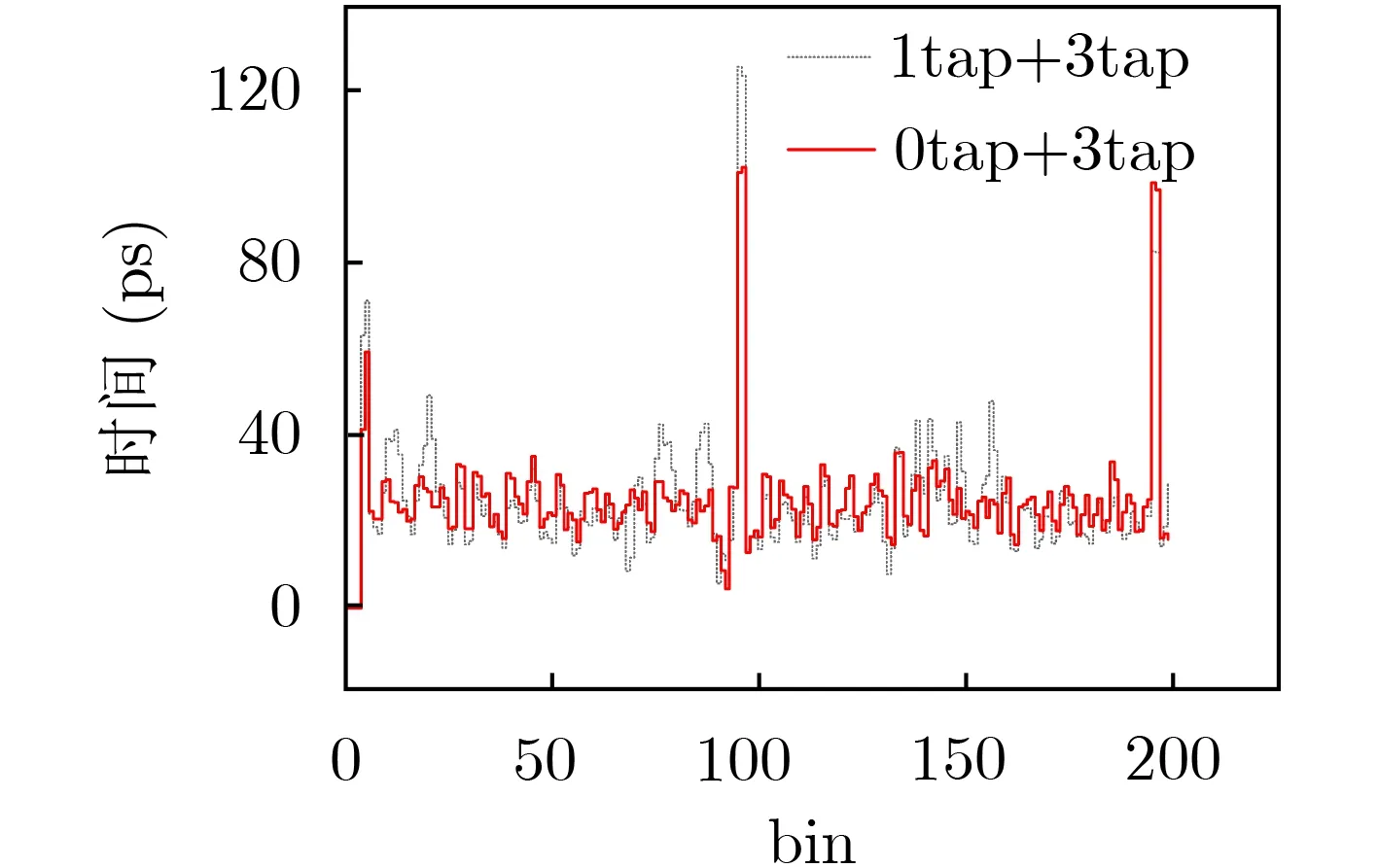
图6 两种2抽头方式的码宽典型值
在“0tap+3tap”抽头方式下,利用文中所述方法,校准得到TDC的抽头数量和延迟时间的值,经过线性拟合之后的结果如图7所示,时间分辨率为24.9 ps,对应plain TDC输出二进制编码的最低有效位(Least Significant Bit,LSB),图7显示的TDC的时间线性度较好,拟合优度为0.9997。图8(a)给出了校准得到的TDC的微分非线性(Differential Non-Linearity,DNL)指标,在“0tap+3tap”抽头方式下,DNL范围(–0.84~3.1)LSB,DNL图中的突出部分对应的抽头位置同图6一致。图8(b)给出了校准得到的TDC的积分非线性(Integral Non-Linearity,INL)指标,在“0tap+3tap”抽头方式下,INL范围(–5.2~2.2)LSB。经过对INL分析得到,在同一个时钟区域内自下向上级联的进位链,越向上,进位链抽头对应的延迟时间值越小,对应到图8(a),抽头位置从0到93,INL是一个缓慢下降的过程,抽头位置从94到193,INL亦如是。对比参考文献[1,2,4,10]中的TDC码宽合非线性参数典型测试结果,本文所述校准方法得到的结果与之符合较好,证明该方法可行。

图7 “0tap+3tap”抽头方式的TDC线性拟合结果
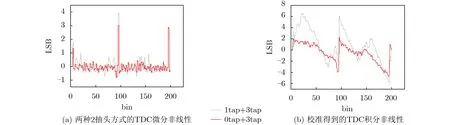
图8 TDC的非线性示意
为了验证基于相干采样的码密度校准结果的稳定性和可重复性,多次校准记录同一个抽头的延时,反复测量36次(校准次数N=36),其分布如图9所示,分别显示了i为92,94,96,98时,共4个码宽及其标准差,i表示抽头位置,ti表示第i个抽头码宽,σi表示第i个抽头标准差,其中抽头94是跨时钟域产生的。可以看到,4个抽头的码宽随时间发生变化,纵轴时间变化范围2 ps,测量36次,同一个抽头码宽的一致性比较好,σi优于0.5 ps,根据前述式(1),已知文中所用校准方法的校准误差最大值στ为5 ps(T=5 ns,N=1000000),σi远小于5 ps。

图9 TDC典型码宽和标准差
5 结论
基于相干采样理论,本文提出并验证了一种通用的TDC码密度校准信号产生方法,确保TDC主时钟和校准信号的频率相干,结合输出保持电路,保证校准用的随机信号在TDC延迟路径上的均匀分布,实现了对TDC的bin-by-bin校准。采用Kintex-7 FPGA内部的进位链实现plain TDC,并利用所述的方法校准plain TDC的码宽,研究测试了2抽头方式下的TDC性能参数,在“CO0+CO3”的抽头方式下,时间分辨率(对应LSB)为24.9 ps,微分非线性为(–0.84~3.1)LSB,积分非线性为(–5.0~2.2)LSB,该测试方法得到的结果和经典文献[1,2,4,10]给出的测试结果符合较好。多次测试考核结果表明:文中所述方法采用的时钟逻辑,单个延时单元的标准差优于0.5 ps。对比两种经典的基于组合逻辑电路的码密度校准信号产生方法,本文基于相干采样理论,提出了利用时钟逻辑资源产生校准信号的方法,校准结果的稳定性和重复性好。本文提出的通用码密度测量方法同样适用于其他类型的TDC的码密度校准。

