基于稀疏面阵的低复杂度三维信源定位算法

吴皓威 舒 畅 欧静兰 杨士中

①(重庆大学通信与测控中心 重庆 400044)

②(重庆大学微电子与通信工程学院 重庆 400044)

③(空天地网络互连与信息融合重庆市重点实验室 重庆 400044)

1 引言

近场信源定位技术在射频标签定位[1]、麦克风阵列声源定位[2]、被动声呐定位[3]、5G毫米波终端定位[4]等领域有着广泛的应用。在近场信源定位中，接收机处于信源天线的菲涅尔区[5]。3维信源定位[6]是近场信源定位中最具有现实意义的形式，其通过具有2维平面性质的接收阵列对近场信源进行3维度精确定位，获得距离、方位角与俯仰角信息。

波达方向估计(Direction Of Arrival,DOA)算法是实现3维信源定位的主要方法之一。近年来，为了提高信源定位的精度，学者对多重信号分类

(MUltiple SIgnal Classification,MUSIC)算法[7]与借助旋转不变性估计信号参数算法[8]进行了广泛的研究[9]。然而MUSIC算法虽然拥有了超分辨率的DOA估计精度，但是需要对每个参量进行谱峰搜索，复杂度较高；而且随着搜索维度的增加，复杂度会急剧上升。因此，极高的复杂度一直是制约MUSIC算法在信源定位领域应用的主要问题。

现有文献在降低基于MUSIC信源定位算法复杂度方面做了大量的工作。文献[10]提出了一种基于求根公式法的优化算法，此算法将谱峰搜索转换为多项式根的搜索，在一定程度上降低了复杂度。文献[11,12]提出了针对2维信源定位的降维优化算法，其将2维面阵谱峰搜索降维成1维线阵谱峰搜索，此算法在阵元数量较大时优化效果极为明显。文献[13]针对基于线阵的近场定位提出了一种降秩优化MUSIC算法，利用泰勒公式将2维导向矩阵中的距离与方位角剥离，并分别进行谱峰搜索。文献[14]提出了一种稀疏面阵(Sparse Planar Array,SPA)结构，其利用互素的稀疏结构，极大程度地减少了阵元数量，降低了算法的复杂度。文献[15]提出了以L型阵列结构进行3维近场测量的结构模型，该结构与面阵结构相比具有较低的结构复杂度，与双平行线阵结构[16]相比具有更好的定位精度。从现有文献来看，针对3维信源定位的低复杂度MUSIC算法研究较少，而且复杂度仍然较高，难以在实际工程中应用。

针对3维信源定位中计算复杂度过高的问题，本文提出一种基于互素线阵互素平移的稀疏面阵(Coprime Linear Array Coprime Shift-SPA,CLACS-SPA)的3维降秩MUSIC(RARE-MUSIC)算法。所提CLACS-SPA模型是由稀疏线阵变换得到的，减少了阵元数量，降低了结构复杂度。所提算法将3维谱峰搜索转化为对方向角俯仰角的2维搜索和距离项1维搜索，减小了谱峰搜索范围，降低了算法的复杂度。通过仿真分析得到如下结论：(1)在相同口径与定位算法条件下，所提结构相较于均匀面阵结构在复杂度上有了一定的降低；(2)在相同的口径与CLACS-SPA结构下，所提算法相较于经典3维MUSIC算法在复杂度上优化效果极为明显；(3)在相同口径和阵元数量条件下，相较于经典3维MUSIC算法，所提算法在俯仰角和方向角的测量上有了很大的提升。此外，本文还研究了信噪比、互素因子对本算法定位精度的影响。

2 基于互素线阵互素平移的稀疏面阵构建

均匀平面阵列(Uniform Planar Array,UPA)是一种经典模型，其相邻阵元间距均为半波长，该模型在3维信源定位时精度较高，但在阵列口径较大时，较高的结构复杂度限制了该模型的应用。为了实现低复杂度的3维信源精确定位，本文提出CLACS-SPA结构，其主要特征是将一列互素线阵(Coprime Linear Array,CLA)沿着与之垂直的方向按照相同的互素规律进行平移而得到。

图1 稀疏面阵阵元构造图

3 近场面阵3 维信源定位

3.1 经典3维MUSIC算法

3维MUSIC(3D-MUSIC)算法是一种对信源的3维参数进行估计的方法，其利用了接收信号中噪声空间与信号空间的正交特性。MUSIC算法的空间谱函数为

3.2 稀疏近场面阵的降秩MUSIC算法

为了缩小搜索范围，减少搜索时间，本文提出一种低复杂度的3维RARE-MUSIC算法，该算法通过泰勒公式分离了方向参数与距离参数，并利用代价函数缺秩的要求，将3维谱峰搜索转化为一个包含方位角与俯仰角的2维谱峰搜索和1个仅含有距离项的一维谱峰搜索。具体方法介绍如下。

3.2.1距离参数分离

3.3 复杂度分析

在3维信源定位中，复杂度是重要的设计指标之一。表1是在方形面阵边长均为12λ，即相同口径的情况下，CLACS-SPA和UPA所需要的阵元数量。从中可以看出，在相同口径下，CLACS-SPA结构比均匀面阵结构所需的阵元数量少，且互素因子的值越大，所需的阵元数量也将越少；所提结构可以有效降低面阵结构复杂度和基于该面阵算法的计算复杂度。

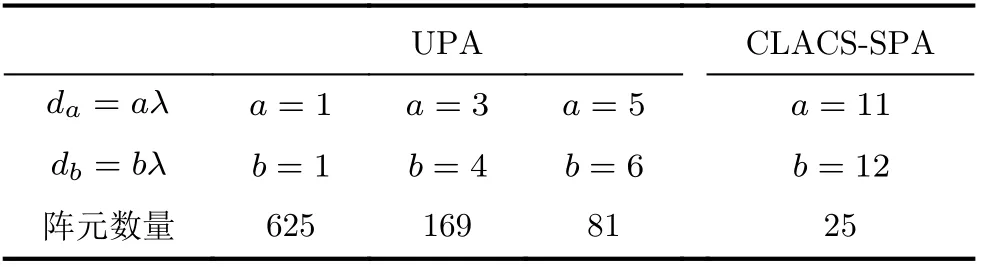
表1 相同口径下，CLACS-SPA和UPA的阵元数量

4 仿真与分析

4.1 信源参数测量仿真

图2给出了所提算法对信源进行3维定位的测量结果图。其中，图2(a)是剥离了距离参量r后，俯仰角与方位角搜索的空间谱图；图2(b)为针对距离r搜索的空间谱图。由图2可以看出，所提算法仿真结果谱峰都相当突出，获得的估计值与真实值非常接近，从而验证了所提算法对于3维信源定位的可行性。

图2 信源位置测量结果图

4.2 复杂度对比分析

图3给出了3种近场算法在阵列口径相同的条件下，复杂度随着口径变化的关系曲线。其中横坐标的单位是半波长。从中可以看出：(1)所提算法复杂度最低，具有较强的工程实用性；(2)在相同CLACS-SPA结构下，所提算法相较于经典3维MUSIC算法复杂度降低了2到3个数量级；(3)在定位算法相同的条件下，CLACS-SPA结构相较于UPA结构复杂度降低了1至2个数量级。

图3 算法复杂度随口径变化对比图

4.3 信噪比对测量精度的影响

图4给出了阵列口径相同的条件下3种算法在对俯仰角、方位角以及距离估计的精度与SNR的关系图。从中可以看出：(1)所提算法的测量精度将随信噪比的增加而增加；(2)在阵元数量相同的情况下，所提算法在方位角与俯仰角上相较于经典3D-MUSIC算法定位精度有了较大提升；(3)所提算法在距离项分离中进行了一定的约舍，从而导致所提算法在距离测量上相较于经典3D-MUSIC算法定位精度稍差。

图4 信源位置测量的RMSE与SNR关系图

4.4 互素因子对测量精度的影响

图5给出了在阵列口径相同的情况下，基于3种不同互素因子的所提算法的测量精度随SNR变化的关系图。图5中，阵列边长为2 6λ，信源到接收阵列的距离为70 m。由图可知，互素因子越大阵元数量越少，测量精度越低，表明在一定范围内增加阵元数量可以提升所提算法的测量精度。在阵列口径固定的情况下，由于阵元数量与所提算法的复杂度直接相关，故可以通过控制所提算法的复杂度来获取不同的定位精度。

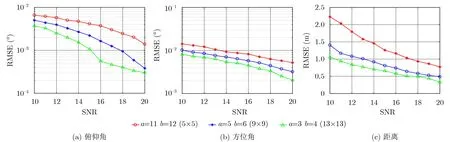
图5 信源位置测量的RMSE与互素因子的关系

5 结束语

在MUSIC算法中，复杂度一直都是制约该种超分辨率算法应用与深入研究的主要问题之一。在新兴的5G毫米波通信系统中，由于采用了大规模阵元阵列、毫米波、小蜂窝覆盖等技术，阵元孔径并不一定远小于收发两端的距离，在这样的场景下，3维信源定位的应用会更加广泛。然而信源的3维定位中，庞大的阵元数量以及对3个参量的谱峰搜索都极大地增加了算法的复杂度。本文提出的基于CLACS-SPA结构的3维RARE-MUSIC算法是一种高效且精确的近场信源定位算法，可以很好地降低复杂度并完成对信源的精确定位。仿真与分析结果表明，与常规算法相比，所提算法不仅降低了运算复杂度，而且提高了对于角度的定位精度，具有较好的工程实用性。