结合多源特征与高斯过程模型的SAR图像目标识别*
辛海燕,童有为
(1.桂林航天工业学院 电子信息与自动化学院,广西 桂林 541004;2.桂林电子科技大学 信息与通信学院,广西 桂林 541004)
0 引 言
合成孔径雷达(Synthetic Aperture Radar,SAR)通过高分辨率成像对关心区域进行观测与情报分析。SAR目标识别技术主要开展基于图像的目标类别确认,主要涉及特征提取和分类决策两个阶段[1]。应用于SAR目标识别的特征包括几何形状、投影变换以及电磁散射等特征。文献[2]和文献[3]分别采用目标轮廓、区域作为SAR目标识别的基本特征。Mishra[4]分别利用线性鉴别分析(Linear Discriminant Analysis,LDA)和主成分分析(Principal Component Analysis,PCA)进行SAR图像特征及目标识别。文献[5]将核主成分分析(Kernel PCA,KPCA)用于SAR目标识别。Cui等[6]基于非负矩阵分解(Non-negative Matrix Factorization,NMF)设计SAR目标识别方法。Dong等将单演信号用于SAR图像分解,获得相应的特征矢量[7]。文献[8]采用模态分解获得多层次特征用于SAR目标识别。文献[9-10]采用基于属性散射中心匹配进行SAR目标识别。在提取特征的基础上,分类决策过程主要采用各类分类器判决待识别样本的类别。典型的分类器包括支持向量机(Support Vector Machine,SVM)[11-12]、稀疏表示分类(Sparse Representation-based Classification,SRC)[13]等。近年来,基于深度学习模型的SAR目标识别方法也得到了广泛研究,其中最具代表性的是卷积神经网络(Convolution Neural Network,CNN)[14-15]。为了有效结合多类特征的优势,研究人员还提出了多特征融合的方法。张新征等[16]提出基于多特征-多表示的SAR目标识别方法,采用稀疏表示和协同表示分类器对PCA、小波分解以及Zernike矩特征进行融合。代雪峰等[17]采用SRC分别对PCA、NMF和KPCA进行决策,进而采用线性加权融合进行融合。文献[18]采用多任务压缩感知对PCA、NMF以及KPCA进行联合表示及分类识别。文献[19]针对PCA、峰值及轮廓特征提出一种层次化决策融合策略,在结合三者优势的情况下保持识别效率。这些多特征方法验证了其相对传统单一特征的优势。文献[20]提出一种决策可靠性分析方法并用于多特征决策融合。
本文提出一种结合多源特征与高斯过程模型的SAR目标识别方法,采用PCA、NMF及单演信号对SAR图像进行特征提取。这三类特征从不同方面描述SAR图像中的目标特性。分类决策阶段,基于高斯过程模型构建多元分类器,对融合后的三类特征的特征矢量进行决策。作为一种贝叶斯框架下的统计学习方法,高斯过程模型通过非参数概率模型建立输入、输出之间的非线性回归关系。相比传统的SAR目标识别方法,本文方法的主要创新在于高斯过程模型基于贝叶斯理论可获得统计意义上的最佳解决从而提高SAR目标识别方法的整体性能。为对提出方法进行测试验证,基于MSTAR数据集分别设置3类目标、10类目标、型号差异及俯仰角差异4种场景。通过与几类现有的单一特征和多特征融合方法对比,实验结果证明了所提方法的有效性和稳健性。
1 多源特征提取
本文提取SAR图像的多源特征共同描述其中的目标特性,通过结合这些特征可为后续的分类决策提供更为有力的支撑。具体采用的PCA、NMF及单演信号实施过程如下。
1.1 经验模态分解(EMD)
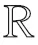
(1)
进而,计算X的协方差矩阵:
(2)
对Q进行特征值分解:
[V,Φ]=eig(Q)。
(3)
式中:Q的特征值和特征向量分别存储在向量V和矩阵Φ中。选取若干较大特征值对应的特征向量,便可以构建PCA的投影变换矩阵,用于原始数据的变换降维。
1.2 非负矩阵分解(NMF)
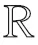
Λ≈GH,Λij,,Gi,u,Hu,j≥0。
(4)
式中:Λij,、Gi,u、Hu,j分别为对应矩阵中的元素。在非负约束下最小化重误差,过程如下:
(5)
如式(5)所示,NMF的目标时获得最佳的G和H,但同时求解两者显然是一个非凸的优化问题。为此,NMF实施过程中采用迭代最优化方法进行求解,更新表达式如下:
(6)
(7)
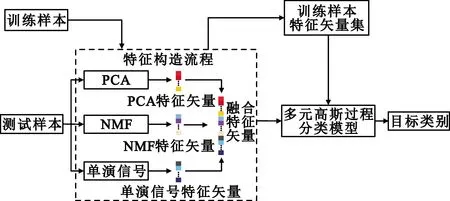
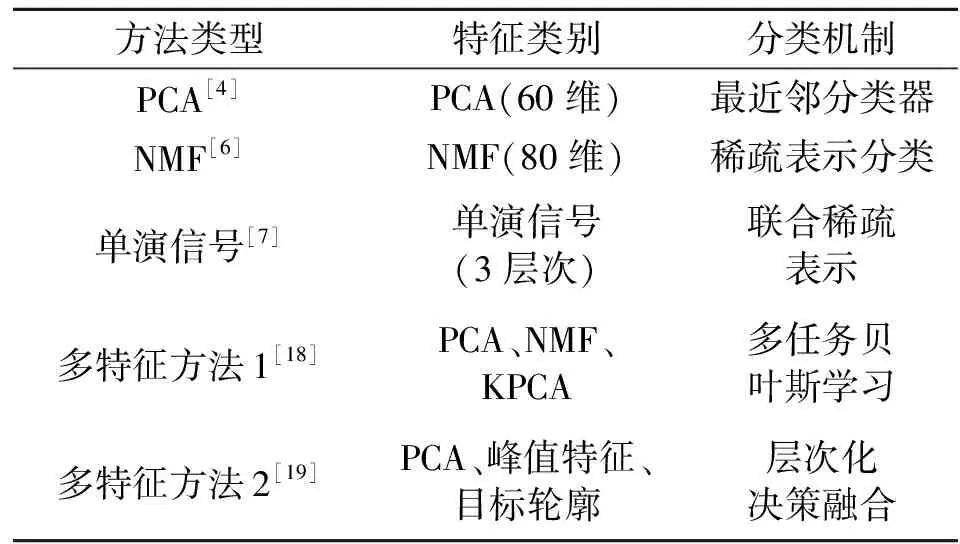
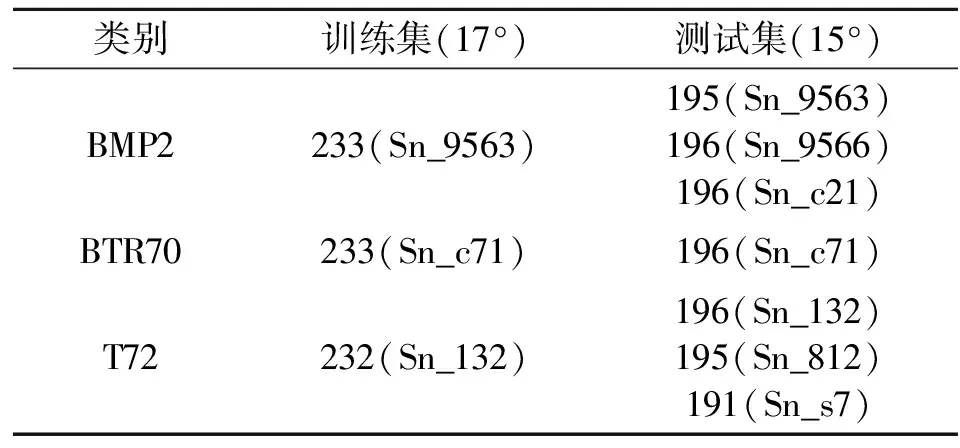
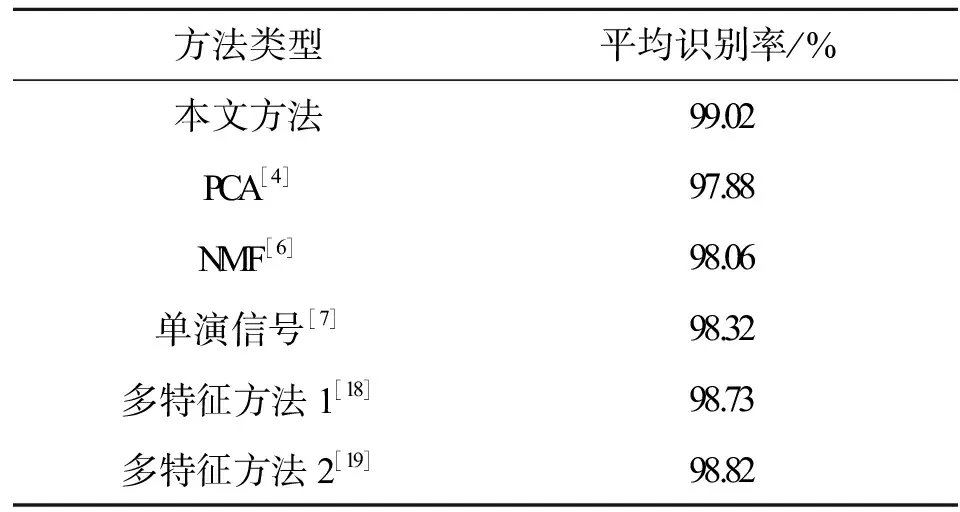
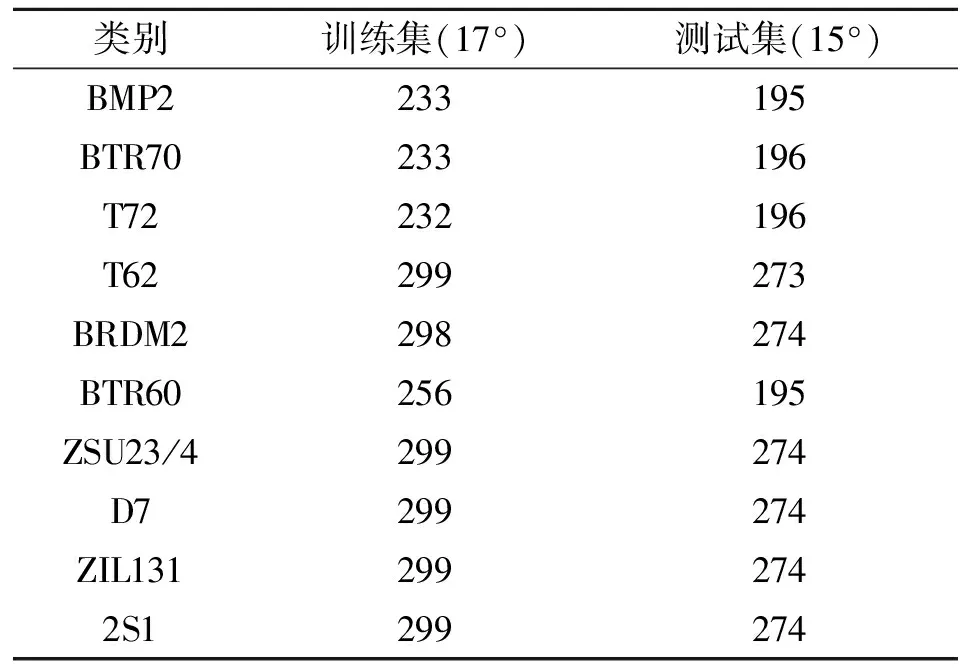
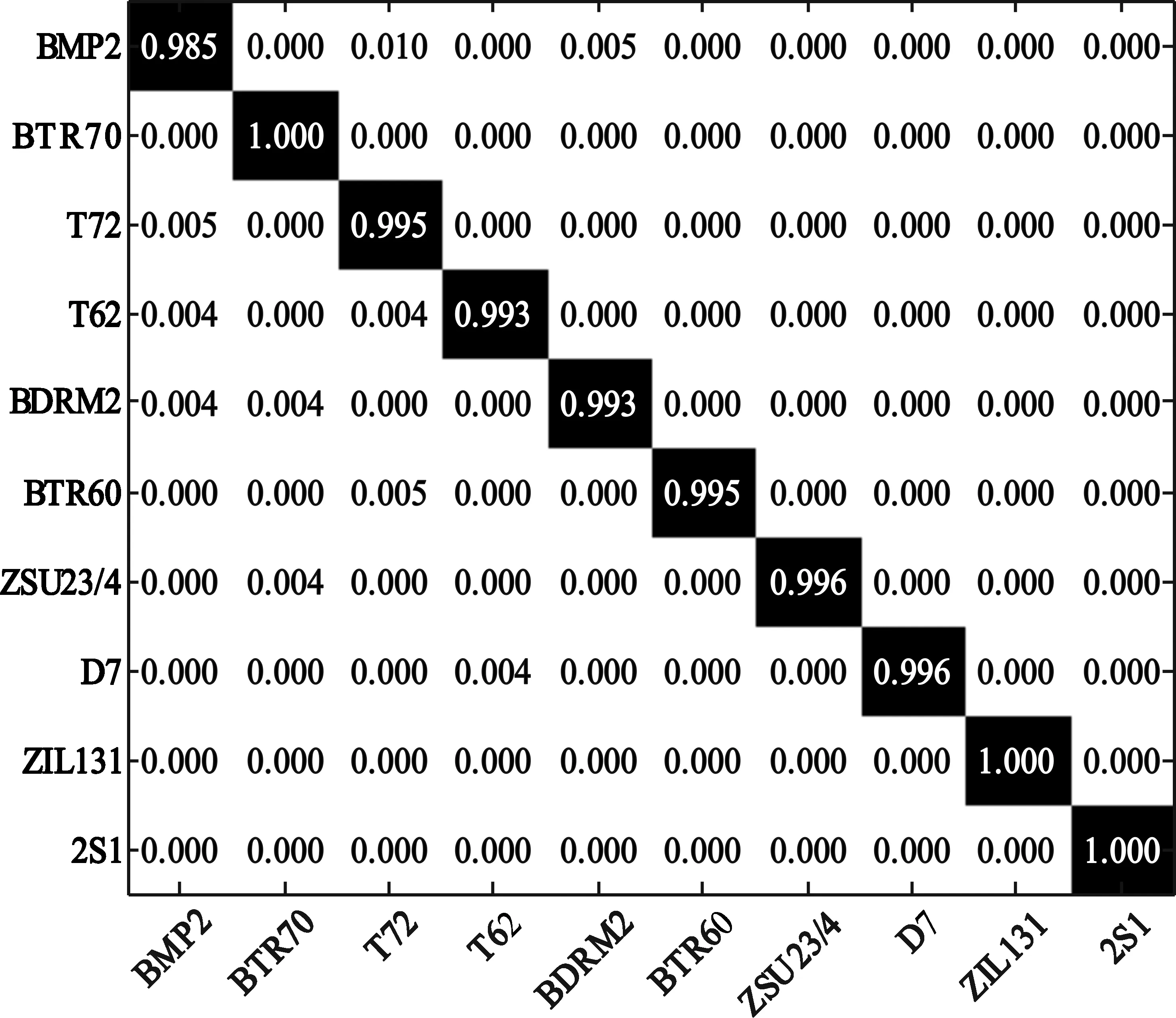
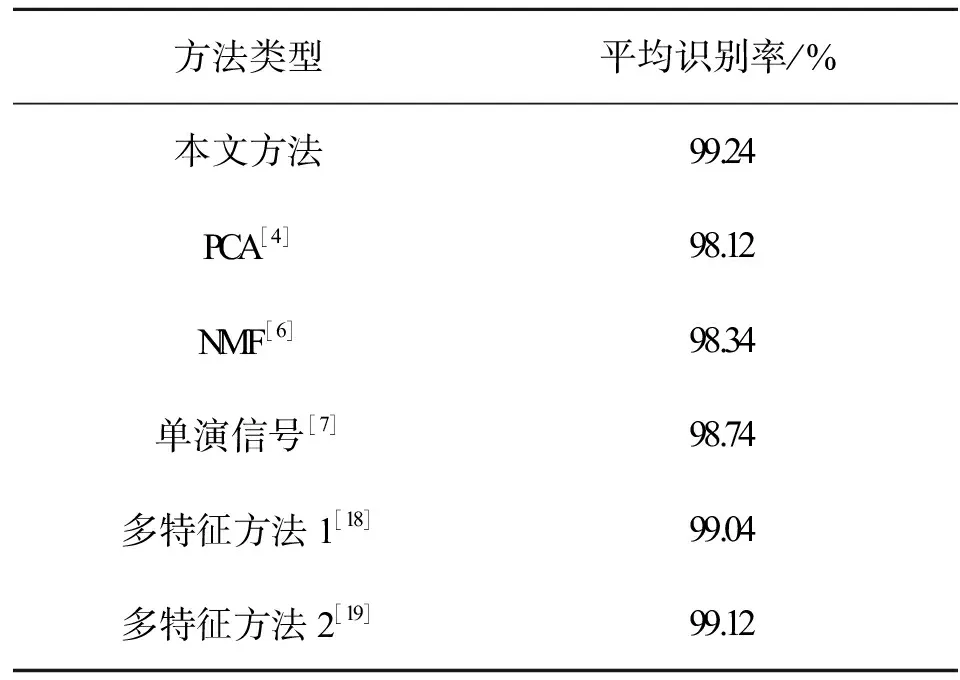
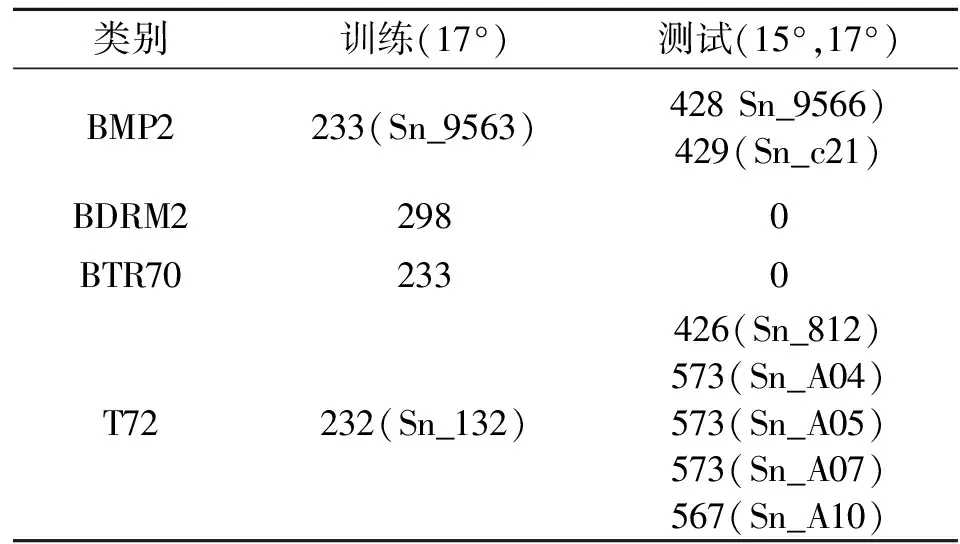
式中:0≤a 在式(6)和式(7)的更新下,可计算不同迭代次数下的重构误差。但迭代次数达到预设最大值或重构误差小于预设门限时,迭代终止输出最佳的矩阵G和H。此时,便可以采用G-1作为投影矩阵对原始数据实施降维,获得相应的特征矢量。 (8) Riesz变换的频域表达式为 (9) 那么,输入图像f(z)的Riesz变换定义如下: fR(z)=(fx(z),fy(z))=(Rx*f(z),Ry*f(z))。 (10) 式中:*代表卷积操作。 一般地,采用带通型Log-Gabor滤波器可获得多尺度、多层次的单演型号分解结果。Log-Gabor的频率响应定义为 G(ω)=exp{-[lg(w/w0)]2/(2[lg(σ/w0)])}。 (11) 式中:w0表示滤波器中心频率,σ为尺度变量。在此基础上,基于滤波的单演信号进一步描述为 flg-M(z)=(flg(z),flg-x(z),flg-y(z))= (flg(z),Rx*flg(z),Ry*flg(z))。 (12) 式中:flg(z)=f(z)*F-1(G(ω)),F-1表示二维傅里叶逆变换。 根据上述过程,基于单演信号定义图像局部幅值A(z)、相位φ(z)、方向θ(z)如下: (13) 文献[7]对单演信号在SAR目标识别中的应用进行了分析,本文采用其中相同思路对SAR图像进行分解,获得相应的幅度、相位和方位成分,然后对各个成分进行降采样及串接,获得单一特征矢量。 上述三类特征具备从不同侧面描述SAR图像目标特性的能力:PCA在线性空间获取SAR图像的低维表示;NMF在非负约束下获得特征矢量;单演信号则分解得到多层次幅度、相位、方向等信息。因此,通过有效结合三类特征矢量可有效提升后续的分类提供更充分的信息,提升决策整体稳健性。 高斯过程模型通过概率建模的方式建立回归模型,建立输入、输出之间的映射关系[22-23]。本文基于高斯过程模型构建多元分类器,用于多类别SAR目标识别问题。 高斯过程模型一般包括似然函数定义、隐变量函数定义和后验概率计算三个关键环节。在利用高斯过程模型进行二元分类时,关键在于采用高斯函数对分类问题中的隐变量函数进行逼近,最终计算新样本属于不同类别的后验概率。 (10) 假设fi服从零均值多维高斯分布,则先验概率p(f|X)建模如下: (11) 式中:K代表f的协方差矩阵。根据贝叶斯理论,获得隐函数的后验概率为 (12) 式中:p(y|f)为似然函数,p(y|X,θ)为边缘概率分布。本文采用Laplace逼近方法求解后验概率p(f|X,y,θ)的估计值q(f|X,y,θ)。将lgp(f|X,y,θ)在最大后验概率处的f按二阶泰勒级数展开,获得高斯估计如下: (13) φ(f)=lgp(y|f)+lgp(f|X)= (14) 可得到后验概率为 p(f|X,y,θ)≈q(f|X,y,θ)= (15) 边缘概率分布可表示为 (16) (17) (18) 根据y*=1和y*=-1的概率大小,即可实现测试样本的二元分类。 上述介绍的高斯过程模型可直接用于二元分类。对于多类别识别问题,需要对原始的二元分类进行拓展,其中较为经典的策略是采用一对一投票机制。对于k类识别问题的分类模型构建过程归纳如下: (1)训练阶段 (2)分类阶段 基于投票机制对待识别样本x*的类别进行分类。首先,将每个类别的初始票数均设置为0;然后,利用训练阶段得到的k(k-1)/2个二元分类器对测试样本进行分类,当分类器Ci,j将x*判别为第i类,则类别i的得票数加1。最终,根据各个类别的总得票数,测试样本x*的类别判决为得票数最高的类别。 在基于高斯过程模型构建多元分类器的基础上,本文采用其对提取的PCA、NMF以及单演信号特征进行分类,基本过程如图1所示。首先,对于PCA、NMF以及单演信号的特征矢量进行序贯串接处理,获得融合后特征矢量。按照这一特征构造过程构架所以训练样本的特征矢量集,并用于多元高斯过程分类器的训练。然后,对测试样本按照相同的特征构造算法获得融合后的特征矢量。最终,直接采用训练后的高斯过程分类模型进行类别确认,获得测试样本所属的目标类别。 图1 本文方法的识别流程 本文基于MSTAR数据集对提出方法进行性能测试。该数据集是目前SAR目标识别方法测试和验证的权威数据集,其中包含的地面目标如图2所示。各类目标SAR图像样本丰富,覆盖0°~360°方位角,方位和距离向分辨率均为0.3 m。根据现有文献可知,基于MSTAR数据集可设置多种操作条件进行测试,包括标准操作条件和扩展操作条件。 图2 10类MSTAR目标的光学(上)及SAR图像(下) 测试中,将提出方法与现有几类SAR目标识别方法进行对比,包括基于单一特征的方法和多特征融合的方法,具体介绍如表1所示。所有方法均在相同的硬件平台运行和测试(英特尔i7处理器,3.4 GHz主频,8 GB RAM)。 表1 实验中设置的对比方法 3.2.1 标准操作条件 (1)3类目标识别问题 首先在标准操作条件下对3类目标识别问题进行测试,训练和测试样本如表2所示,分别来自17°和15°俯仰角。其中,BMP2和T72的测试样本相比训练样本包含更多的型号。采用各类方法对测试样本进行识别,统计平均识别率如表3所示。与3类基于单一特征的方法相比,本文通过结合它们并采用高斯过程模型进行分类,显著提升了融合后的识别性能。与其他两类多特征方法相比,本文通过高斯过程模型获得了概率意义上的最佳决策结果,因此识别率更高。3类目标识别问题的结果表明了本文方法具有更强的有效性。 表2 3类目标的训练和测试集 表3 各类方法对3类目标的平均识别率 (2)10类目标识别问题 相比3类目标识别问题,10类目标识别涉及的类别更多,区分难度更大。表4设置了10类目标识别问题的训练和测试样本。与3类目标识别问题相比,本实验中去除了BMP2和T72中的其他型号。图3显示了本文方法对这10类目标的识别结果,图中对角线元素分别对应不同类别的正确识别率。统计全部10类目标,求得平均识别率为99.24%。表5对比了各类方法对10类目标的平均识别率,其结果与3类目标识别问题基本一致。本文方法相比单一特征识别方法性能优势十分显著。与其他两类多特征方法相比,本文通过高斯过程模型获得了更为精确的识别结果,最终性能也优于它们。10类目标识别问题的结果进一步验证了本文方法在标准操作条件下的有效性。 表4 10类目标的训练和测试集 图3 本文方法对10类目标的识别结果 表5 各类方法对10类目标的平均识别率 3.2.2 扩展操作条件 (1)型号差异 型号差异指的是测试样本与训练样本来自相同目标的不同型号。表3中的3类目标识别问题设置了一定的型号差异,上但差异相对较小。表6设置了本实验的训练和测试样本。其中,测试样本的BMP2和T72目标包含多个不同的型号。对各类方法在当前条件下进行测试,统计平均识别率如表7所示。可见,本文方法平均识别率最高,验证了其对于型号差异的稳健性。与单一特征方法相比,本文的性能提升十分显著,表明结合3类特征的优势和高斯过程模型可有效提升识别方法对型号差异的稳健性。对于其他两类多特征方法,本文通过高斯过程模型可以更为有效地发挥参与融合的特征的用处,从而获得更为可靠的识别结果。实验结果表明本文方法对于型号差异具有更强的稳健性。 表6 型号差异条件下的训练和测试集 表7 各类方法在型号差异下的平均识别率 (2)俯仰角差异 俯仰角差异指的是测试样本与训练样本来自差异较大的俯仰角,具体设置如表8所示。2S1、BDRM2和ZSU23/4 3类目标训练样本来自17°俯仰角,但测试样本分别来自30°和45°俯仰角。图4统计了各类方法在两个俯仰角下的平均识别率。在30°俯仰角时,各类方法的识别率仍可以保持在90%以上;但在45°俯仰角时,各方法的平均识别低至75%以下。由于较大的俯仰角差异,导致各类方法的性能都出现了较为显著的下降。本文方法采用高斯过程模型融合3类特征的优势,最终显著提升了在俯仰角差异条件下的识别性能。对比可见,本文方法对俯仰角差异的稳健性更强。 表8 俯仰角差异下训练和测试样本 图4 各方法在俯仰角差异下的平均识别率 本文提出结合多源特征与高斯过程模型的SAR图像目标识别方法,通过提取SAR图像的PCA、NMF以及单演信号特征矢量共同描述目标特性,实现多层次描述。对它们进行串接处理,获得统一的特征矢量。采用多元高斯分类模型对融合后的特征矢量进行分类,发挥各类优势的优势,获得概率意义上的最佳分类结果。实验中,采用MSTAR数据集设置3类目标识别、10类目标识别、型号差异以及俯仰角差异的条件对提出方法进行综合测试,实验结果验证了本文方法相比现有几类方法具有更强的有效性和稳健性。1.3 单演信号
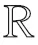
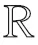
2 高斯过程模型
2.1 二元分类
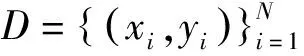
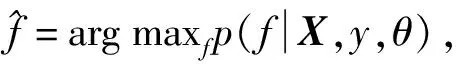
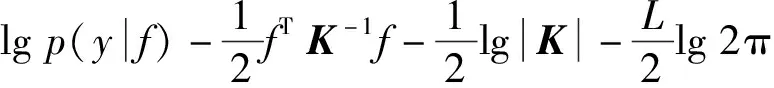
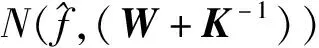
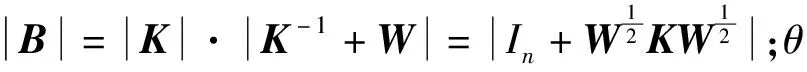
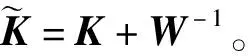
2.2 识别方法

3 实验结果与讨论
3.1 数据集与对比方法

3.2 实验结果与分析



4 结 论

