一种适合低轨卫星通信的宽带传输技术*
熊 韬,廖世文
(广州海格通信集团股份有限公司,广州 510663)
0 引 言
低轨卫星通信系统凭借其运行轨道低、传输时延短、覆盖范围广及组网灵活等优势,可以在任意时间、任意地点和用户对接,让全球的用户享受全方位的通信服务[1]。正是由于上述优点,20世纪90年代末,以铱星系统为代表的低轨卫星通信迎来了发展热潮。但是限于当时卫星的制造、发射和运营成本高昂,同时地面基站的快速、低成本建设使得绝大多数场景对低轨通信的需求并不是十分迫切,因此在21世纪初低轨卫星通信遇到了发展瓶颈。近年来,随着低轨卫星通信成本的显著下降,以及地面高带宽、低时延的第五代移动通信(5G)技术的逐步商业化,一个以地面5G为基础、低轨宽带通信为重要支撑的空地一体化通信的研究正在成为行业热点。
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术由于其宽带传输性能卓越而被5G所采纳,但是由于卫星通信场景中发射功率受限的问题很突出,直接使用OFDM体制会造成发射信号的峰均比过高,使得功率受限的低轨宽带通信系统很容易进入功放非线性区域,从而导致严重的带内非线性失真。而与OFDM体制具有良好兼容的离散傅里叶变换扩频正交频分复用(Discrete Fourier Transform Spread Spectrum Orthogonal Frequency Division Multiplexing,DFT-s-OFDM)体制在能传输高速率数据的同时具有低峰均比特性,因此可作为较为理想的低轨宽带的传输体制。
1 DFT-s-OFDM体制
OFDM的调制过程可以使用快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)方法来实现:
(1)
式中:Xi为OFDM调制之前的符号,N为IFFT的个数。DFT-s-OFDM 技术是在OFDM的IFFT调制之前对信号使用DFT获得频域信号,然后插入零符号进行扩频,扩频信号再通过IFFT 转换为时域信息,因此DFT-s-OFDM本质上也是一种宽带技术。图1所示为DFT-s-OFDM发送流程。
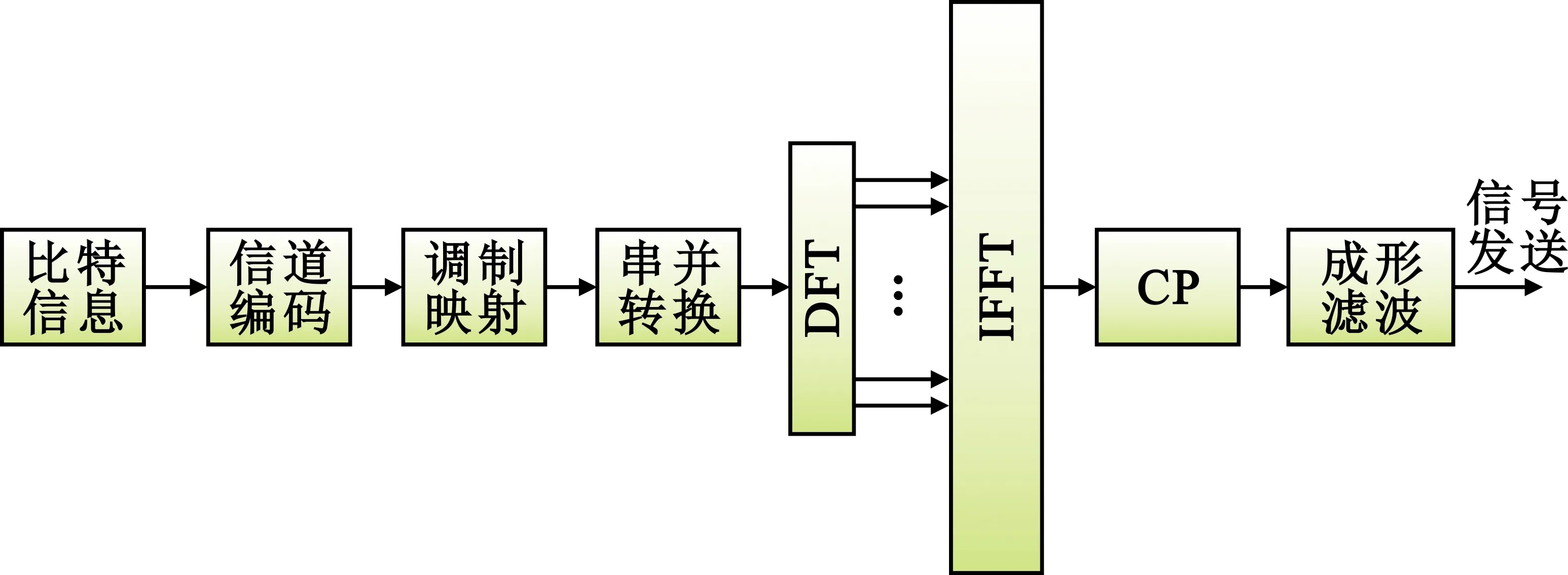
图1 DFT-s-OFDM发送流程
由于DFT-s-OFDM通过一个傅里叶和反傅里叶变换对,IFFT变换后的输出为输入符号的加权叠加,使得DFT-s-OFDM传输体制具有单载波独有的低峰均比(Peak-to-Average Power Ratio,PAPR)特性,此特性正好可以应对卫星通信过程中发射功率受限的场景约束。DFT-s-OFDM体制的低PAPR性决定了其在卫星通信的宽带业务上有着很好的应用前景。
图2是16正交幅度调制方式(16 Quadrature Amplitude Modulation,16QAM)下DFT-s-OFDM与OFDM的信号能量概率密度函数(Probability Density Function,PDF)分布图及累积分布函数(Cumulative Distribution Function,CDF)分布图的仿真结果,可以看出DFT-s-OFDM的峰均比值明显小于OFDM的峰均比值。在CDF图中,若以信号能量分布小于10-6为标准比较DFT-s-OFDM和OFDM的峰均比,可以看出信号能量分布为10-6时,DFT-s-OFDM对应的峰均比值为2.73 dB,而OFDMA对应的峰均比值为3.73 dB。因此,OFDM的PAPR比DFT-s-OFDM的PAPR高2.7 dB,这说明DFT-s-OFDM相比OFDM具有更低的PAPR。
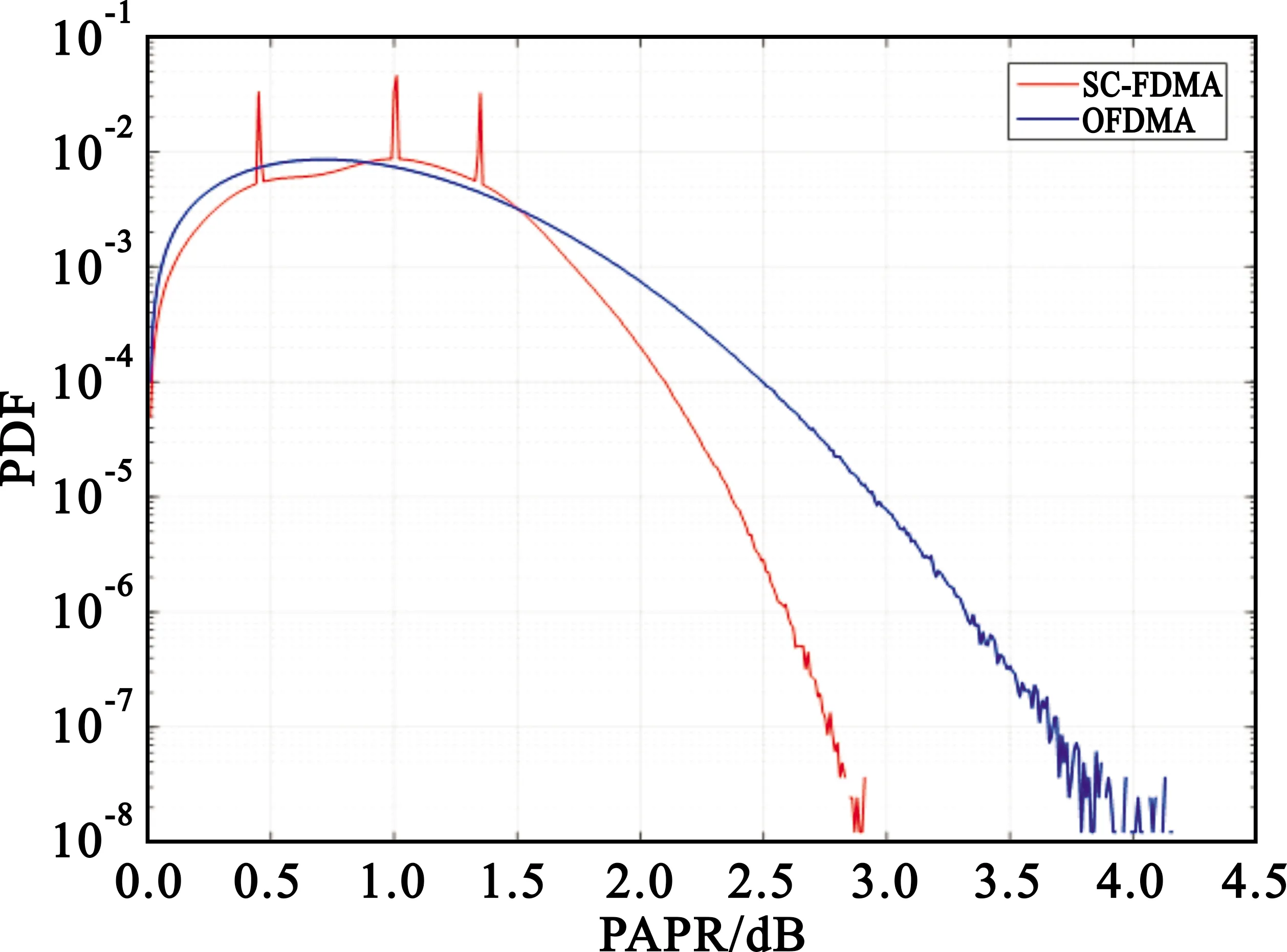
(a)PDF分布图
2 低轨卫星与接收机相对运动对宽带波形产生的影响
宽带信号的波形结构会随着低轨卫星和接收机之间距离的变化出现两个维度的影响:一个是相对运动产生的多普勒频移,另一个是DFT块的采样偏差。
如图3所示,假设卫星所在轨道与地球质心的距离为Re,接收机与通信卫星之间的距离为Rp,地球的半径为R0,卫星速度是vs,载波频率为fs,信号带宽为fd。
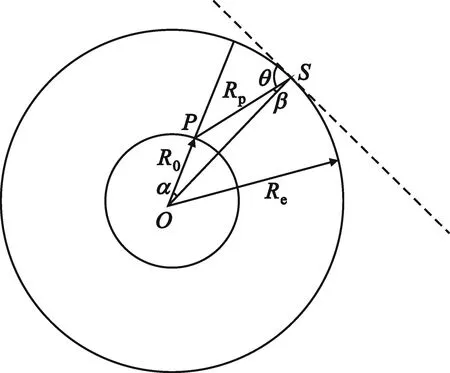
图3 多普勒偏移示意图
接收机位于P点,通信卫星位于S点,两点相对于地心的夹角为α,
(2)
因此,接收机与通信卫星之间的距离为
(3)
由
(4)
得到
β=arcsin(sinαR0/Rp)。
(5)
因而,电磁波到达方向与卫星移动速度方向之间的夹角为
(6)
可知,多普勒频偏为
(7)
式中:fs为载波频率,卫星速度是vs,c为光速。所以多普勒频移的变化率为
(8)
接收机与卫星之间的距离为
(9)
接收机和通信卫星之间的距离变化率为
(10)
同时,在接收机收到DFT-s-OFDM信号时,接收机与发射机之间的距离变化会产生一定的采样偏差,所以每个DFT块的最大采样偏差为
(11)
式中:φ=1/fd为每个码片所占用的时间,γ=fd/n0为一个DFT信号所占用的码片长度。
对上述推导进行数值仿真。仿真过程中,假定低轨卫星的运行速度为7.28 km/s,仿真中用时间代替卫星的实际位置,讨论频偏、频偏变化率、每个DFT块的最大采样偏差与卫星位置之间的相关变化曲线。
如图4所示,低轨卫星在运行过程中产生的频偏最高接近400 kHz,这么大的多普勒频偏通过频偏估计算法来补偿是不现实的,即信号在接收前需要进行预补偿。目前成熟的预补偿方式是通过卫星星历推算卫星的位置及接收机的位置信息推算大致的多普勒偏。这其中运算最复杂的是星历解算,一般的做法是通过卫星广播或者是网络定时(通常一天更新一次)传递参数给低轨终端或者低轨信关站并由其自行解算。目前国内“北斗”导航终端模块普遍采用这种方式且实时性都很好,并不十分耗资源。这种方式可以把多普勒频偏残差降至10 kHz以下。

图4 多普勒频偏随卫星位置变化的曲线
图5的仿真结果表明,在设定足够长的时间(如图中7.5 min)下一个OFDM块会偏差0.02个码片,因此在循环前缀(Cyclic Prefix,CP)的长度设计上必须大于该值。
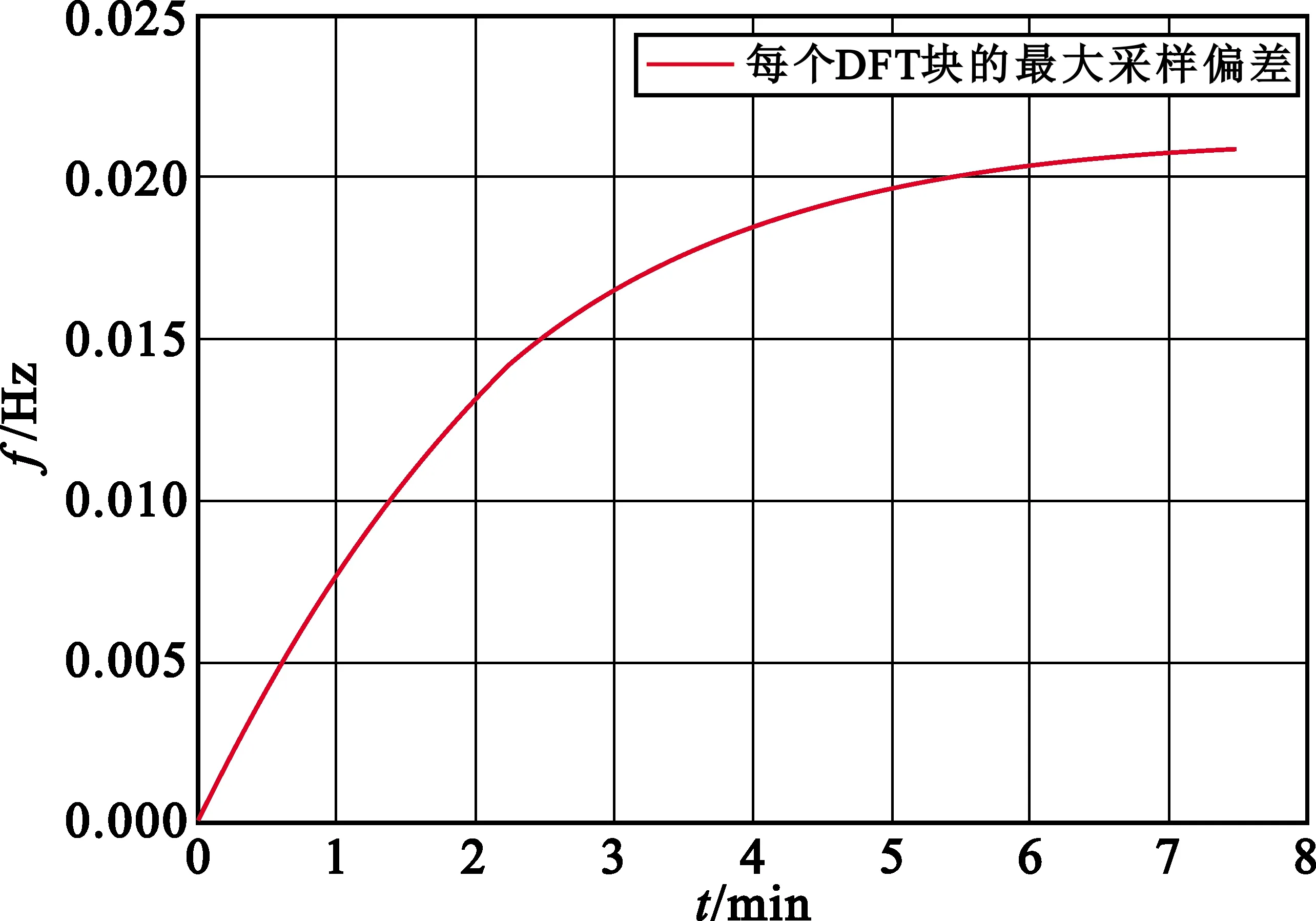
图5 每个DFT块最大采样偏差变化曲线
3 低轨宽带传输波形设计
根据卫星信道的快速时变特性,低轨宽带信号可由同步信道和数据信道组成。同步信道用于卫星信号的快速捕获和失步后的快速同步;数据信道不仅用于数传,同时维护信道的同步和快速跟踪。这里数据信道代表一个数据时隙,每个时隙由4个DFT-s-OFDM块组成。每个同步信道后跟随3个数据时隙,如图6所示。

图6 低轨物理帧结构图
由于接收到的信号存在多普勒频偏残差,数据信道的数据子载波映射的过程中需要插入导频。图7给出了在发送端插入导频的示意图。

图7 导频插入示意图
为应对不同传输速率的需求,本文设计了多档速率波形,具体参数见表1。
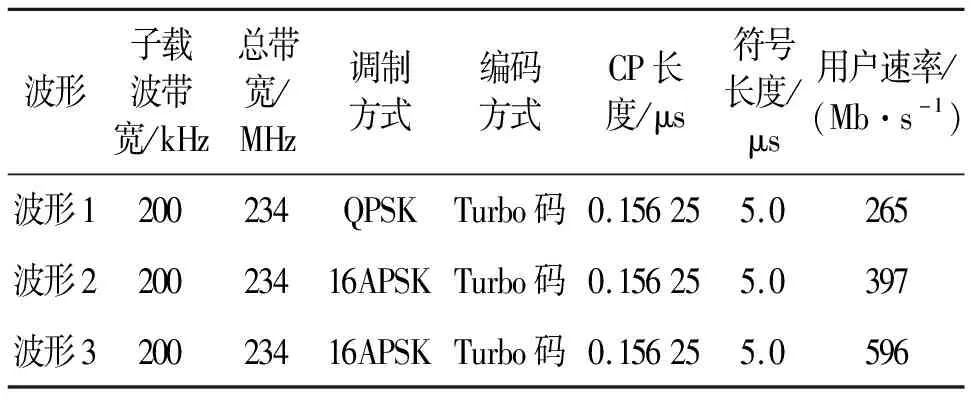
表1 各档速率参数
各档波形的仿真性能如图8所示,表明各档波形在多普勒频偏小于等于10 kHz的情况下均有较好的表现性能,低速率档下波形的抗频偏能力更强。由上一节的分析可知,低轨卫星在实际的运行过程中可以产生近400 kHz的频偏,但是通过星历补偿大部分频偏后,残留频偏值是小于10 kHz的,而上述仿真表明本文所设计的各档波形在频偏10 kHz时的解调性能下降1 dB左右,对实际使用影响不大。

(a)波形1
4 结 论
本文研究了低轨场景下的宽带传输方法。该方法利用DFT-s-OFDM体制所设计的传输波形可以使得传输带宽优于200 MHz,并且通过不同的调制编码组合实现265 Mb/s、400 Mb/s和600 Mb/s的多档传输速率,仿真结果表明在利用星历及接收机位置信息去除大部分多普勒频偏后,本文所提方法具有良好的实用性能。

