比特级码率兼容多元LDPC码打孔算法*

周 华，钱荷玥，王登天，葛旗伟

(南京信息工程大学 电子与信息工程学院，南京 210044)

0 引 言

近20年来，纠错编码技术快速发展。20世纪末，Mackey等人[1]的发现迎来了低密度奇偶校验码(Low-density Parity-check，LDPC)码的研究热潮。而后人们发现多元LDPC(Non-binary LDPC，NB-LDPC)码与码长码率近似的二元LDPC码和Turbo码相比，在中短码情况下其译码性能具有较大增益[2]。如何发挥NB-LDPC码的优势也成为了通信领域值得关注的研究课题。

ITU在移动通信的技术标准中将码率兼容(Rate-compatible，RC)技术确立为核心技术之一，可见实现信息传输速率的可变性已经成为现代通信领域不可或缺的功能之一。其中，码率兼容技术是实现信道编码多重码率的重要手段，通信系统在采用码率兼容码时，可根据当前信道的状态调整码率，确保信息传输的有效性和可靠性。

LDPC码由其特定的校验矩阵定义，码长和码率受校验矩阵的大小限制，在信息传输过程中存在着码率不够灵活的缺点。基于这个问题，Hagenauer[3]在1988年首次提出了码率兼容的打孔型卷积码，通过对编码之后的卷积码(母码)进行打孔，得到了一系列高码率的子码，有效解决了变码率的问题，但打孔位置的选择比较复杂且直接影响译码性能。21世纪初期，Ha等人[4-5]对二元LDPC进行了码率兼容的研究，实现了二元LDPC从低码率到高码率的自由切换。相较于二元码率兼容LDPC(RC-LDPC)码[6-7]，多元码率兼容LDPC(NB-RC-LDPC)码的研究在国际上相对较少。2008年，Klinc等人[8]第一次对多元LDPC码在码率兼容方面进行了研究。2011年，Zhang等人[9]通过将二元打孔方案引入多元打孔，构造了一组基于小环路的多元RC-LDPC码。2016年，Deka等人[10]研究了多元矩阵的短环路并结合环外信息度(Extrinsic Message Degree，EMD)的打孔方案。2018年，穆锡金等人[11]通过掩模矩阵和基矩阵的优化扩展了多元码，得到了一系列码率降低的多元RC-LDPC码。

本文针对多元RC-LDPC码在打孔算法中各码率译码性能不足的问题，提出了一种基于比特级的新型多元打孔算法。该算法将多元LDPC码的打孔节点的选择从符号级扩展到了比特级，并结合多元二进制镜像矩阵的度分布选取较优的打孔变量节点，实现了低码率向高码率之间的转换。仿真验证了该算法的有效性，所构造的NB-RC-LDPC码在较大的码率范围内都能获得较好的译码性能。

1 多元LDPC码译码

与二元LDPC码情况类似，一个M×N多元LDPC码也由其稀疏校验矩阵HNB={hij|i=0,1,2,…,M-1，j=0,1,2,…,N-1}的零域空间所定义，不同的是，HNB中的元素取自伽罗华域GF(q)(q=2m,m=1,2,3…)，即hij∈GF(q)[12]。多元LDPC码与二元LDPC码一样在译码时采用传统置信传播(Belief-Propagation,BP)算法，置信信息在变量节点与校验节点之间交互传递，二元BP译码算法传递的是单比特信息，多元BP传递的是由多个二进制比特信息构成的信息序列，即符号信息。

一个定义在GF(q)上的多元LDPC码，其校验矩阵为

该矩阵的Tanner图如图1所示，可用G={(V，E)}表示，其中V=Vv∪Vc，Vv=(v0,v1,…,vN-1)是变量节点的集合，对应于校验矩阵的列；Vc=(C0,C1,…,CM-1)是校验节点的集合，对应于校验矩阵的行；E是所有连接变量节点和校验节点边的集合。每一条边对应校验矩阵中的非零元hij，与节点相连的边的个数称为节点的度(degree),行重和列重分别表示校验节点和变量节点的度数。

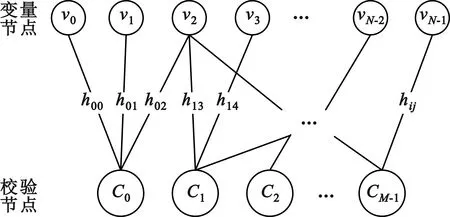
图1 多元LDPC码Tanner图

一个长度为N的向量c,其中c=(c0,c1,c2,…,cN-1),cn∈GF(q),如果满足式(1)，则认为向量c为合法码字。

c·HNBT=0。

(1)

(2)

(3)

多元码字的一个码元由m个二进制比特组成，在译码过程中，码字中的一个比特或是多个比特出现错误，译码器都将这个码字看作译码失败，这使多元LDPC码具备了更好的抗突发噪声的性能[13]。另外，多个比特组成一个码元，在编译码环节码字一次运算m个比特，很大程度上提高了编译码的效率。

2 多元打孔算法

目前，打孔算法是实现LDPC码码率兼容的主要方式之一。打孔算法的含义是通过对部分变量节点作删余处理，从而提高码率。“删余”不是删除对应的码元，是对选定的校验位信息不进行传输。由于接收端在打孔位无法获取有用信息，故译码性能下降。因此多元LDPC码的打孔算法的关键是找出对译码性能影响较小的变量节点，从而尽可能降低性能损耗。

随机打孔算法是目前实现码率兼容的常用方式之一，一个低码率的LDPC母码随机选择不需要传输的码元位置，构造高码率的子码。对于一个码长为N、信息位长度为K(K=N-M)的满秩多元LDPC母码，其码率为R=K/N。若目标码率为R′(R′>R),则需要删余的变量节点个数约为

(4)

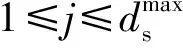
多元LDPC码在传输时，首先将多元码字转化成二进制，即多元符号转化成比特序列[12]。在选择打孔节点时，根据目标码率R′，需要对MR′个符号节点或者(MR′×m)个比特节点进行删余。图2展示了符号级打孔与比特级打孔两种打孔类型。

图2 多元LDPC码打孔

在多元打孔算法中会出现两种情况，其中一种与二元打孔类似，某个变量节点的信息全部删余，即图2中v3的情况，通常称这一类打孔算法为符号级打孔。另一类即在比特向量进行处理，选择合适的比特节点进行删余，但仍保留比特向量中某些比特信息进行译码传输，类似图2中v0和v2的打孔类型，称这一类算法为比特级打孔[14]。相较于符号级打孔算法，比特级拥有更多的可选择性，因此本文基于比特级码元提出了一种新型打孔算法。

3 多元比特级打孔算法

在介绍本文多元打孔算法之前先介绍二进制镜像矩阵的概念。

在伽罗华域GF(q)中，令α为GF(q)的本原域元素，f(α)是其本原多项式，则α的幂次可根据其本原多项式生成所有的非零元素，零元素可表示为全零多项式[15]。假设

f(α)=a0+a1x+a2x2+…+amxm。

(5)

式中：f(α)的最高次幂为m，系数a0,a1,a2…,am∈GF(2)。由α定义的伴随矩阵是一个m×m的二元矩阵K：

矩阵K被称为α在伽罗华域GF(q)的二进制镜像矩阵。

根据上述概念可以将一个大小为M×N多元LDPC码的校验矩阵变为一个Mm×Nm的不规则二元镜像矩阵。二元矩阵的每一列都对应着变量节点的某一个比特信息，为打孔操作提供了更多的选择。根据表1所示的四元域内非零元素的多项式，可得到图3和图4，分别给出了2×3多元矩阵与其对应的二元镜像4×6矩阵的关系图及Tanner图。

表1 四元本原多项式

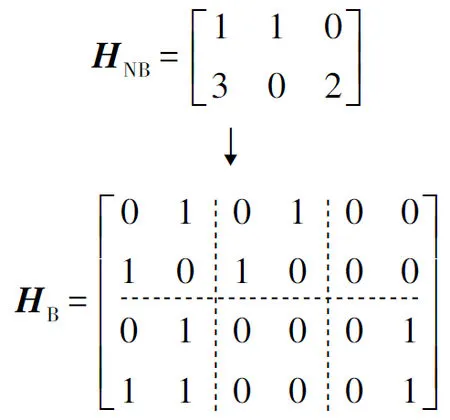
图3 多元矩阵与其二元镜像矩阵关系图

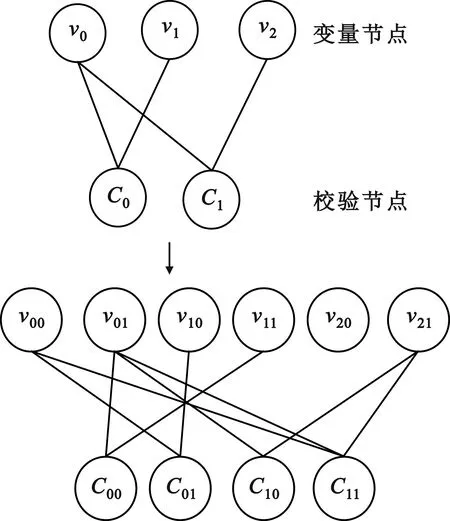
图4 多元LDPC码与二元LDPC码的Tanner图对比

在译码的过程中，列重大的列有助于译码时快速纠错，对应列重小的列的码元发生错误时，对相邻节点的影响相对较小。在将多元矩阵转化成对应的二元镜像矩阵后，可以根据列重的大小即度数的大小来选择合适的打孔变量节点。类似图4中的v20在二进制镜像处理后对译码性能影响最小，故在选择比特节点时可选择v20删余，在保证性能的同时又提高了码率。据此本文提出了一种基于比特级的非随机打孔算法。对于特定的多元M×N矩阵HNB，根据其多元域的本原多项式转化成Mm×Nm的二进制镜像矩阵HB。计算HB中每个变量节点的度数，并将其按由大到小的顺序放入集合G中，输出集合中列重最小的打孔变量节点vab,其中a代表比特节点的符号位，b代表比特位。具体打孔流程如图5所示。

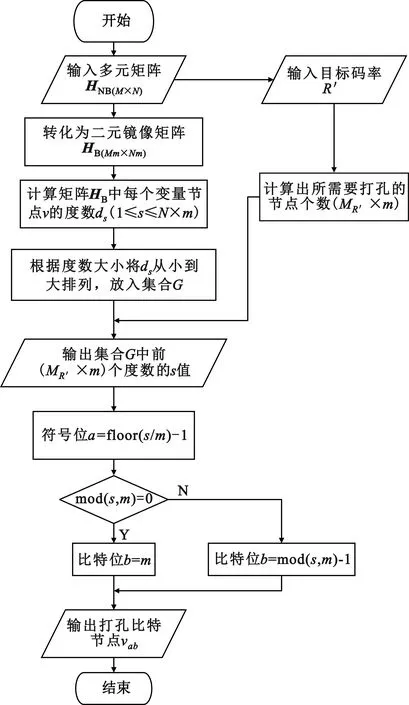
图5 基于比特级的新型打孔算法流程图

比特级新型打孔算法为多元LDPC码码率兼容提供了更多的打孔选择性，算法实质是优先选择度数小的列所对应的变量节点进行删余，从而提高译码性能。在选择打孔节点个数时，所得到的MR′是基于符号级的，故在比特级打孔时需对MR′×m个比特节点进行处理。根据二元镜像矩阵得到的一组比特打孔节点vab(0≤a≤N-1,0≤b≤m-1)，a对应于HNB中的符号位，b对应于符号中m个比特位。

4 仿真与分析

为了验证该打孔算法的译码性能，仿真选用了码长为155、码率为0.4和码长为576、码率为0.5的规则四元LDPC码，与传统的多元符号级随机打孔算法[5]和基于环路的符号级打孔算法[10]作比较，所有实验数据均是在二进制输入加性高斯白噪声(BI-AWGN)信道下仿真获得。译码端采用标准的LLR-BP译码算法，最大迭代次数为50。

图6选用了码长155的四元矩阵分别在BPSK、QPSK、8PSK三种调制方式下进行仿真，分别对10个、20个、30个变量节点进行打孔处理，相较于母码码率分别提高了0.03、0.06和0.1，即码率为0.43、0.46和0.5。当误码率在10-2量级时，9组打孔对比差异不大，但到了10-4量级时，9组数据均获得了0.2～0.4 dB的增益，可见本文算法在低阶调制和高阶调制下都能获得一定程度的增益。

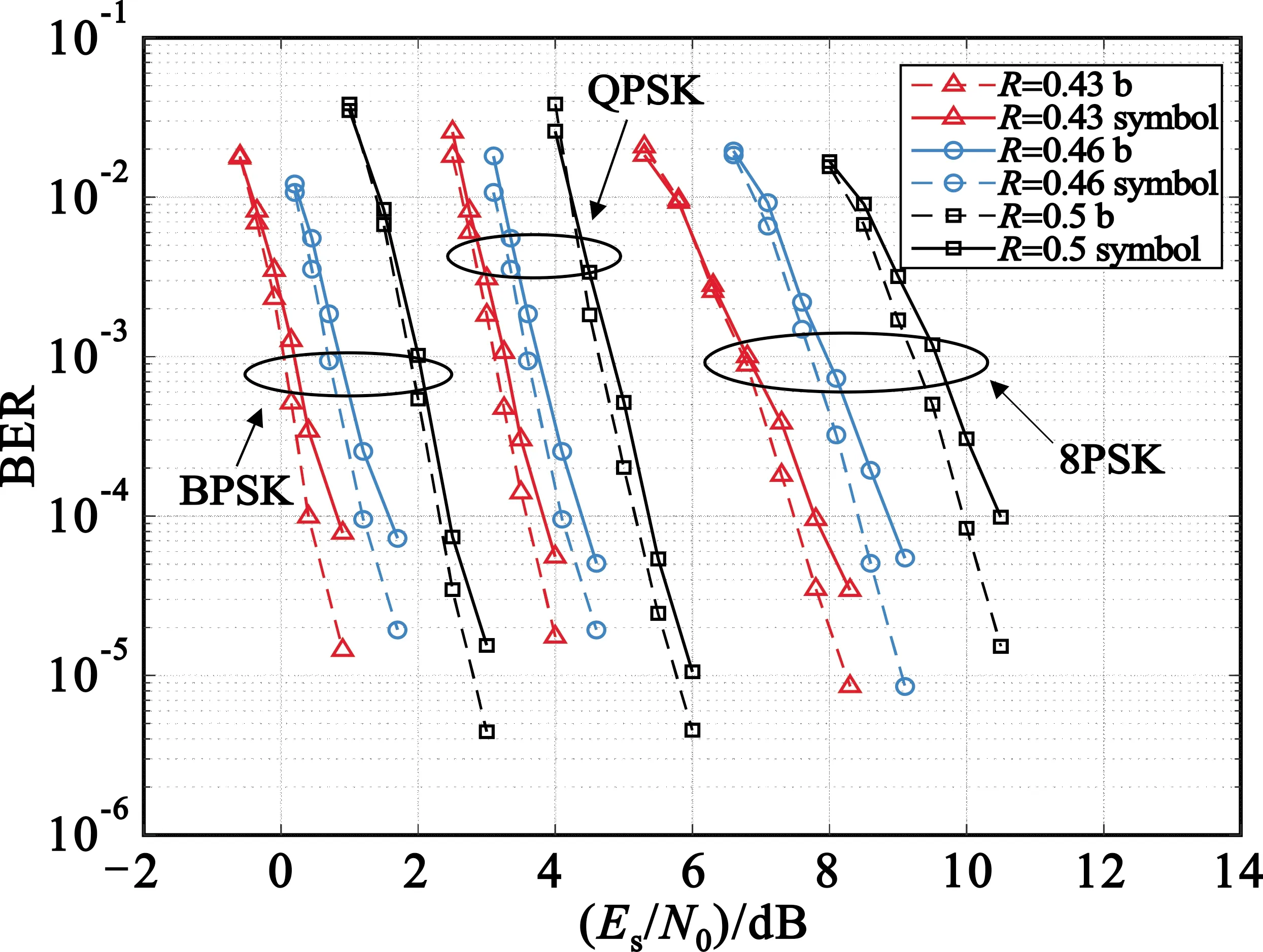
图6 155码长打孔对比图

图7给出了码长576的四元矩阵在BPSK调制下的仿真结果，由图可知码率在0.6和0.7情况下，比特级新打孔算法的性能都优于传统的符号级打孔算法，在10-3量级时两种打孔算法信噪比分别增加了0.25 dB和0.2 dB，实现了码率由低到高的转变。

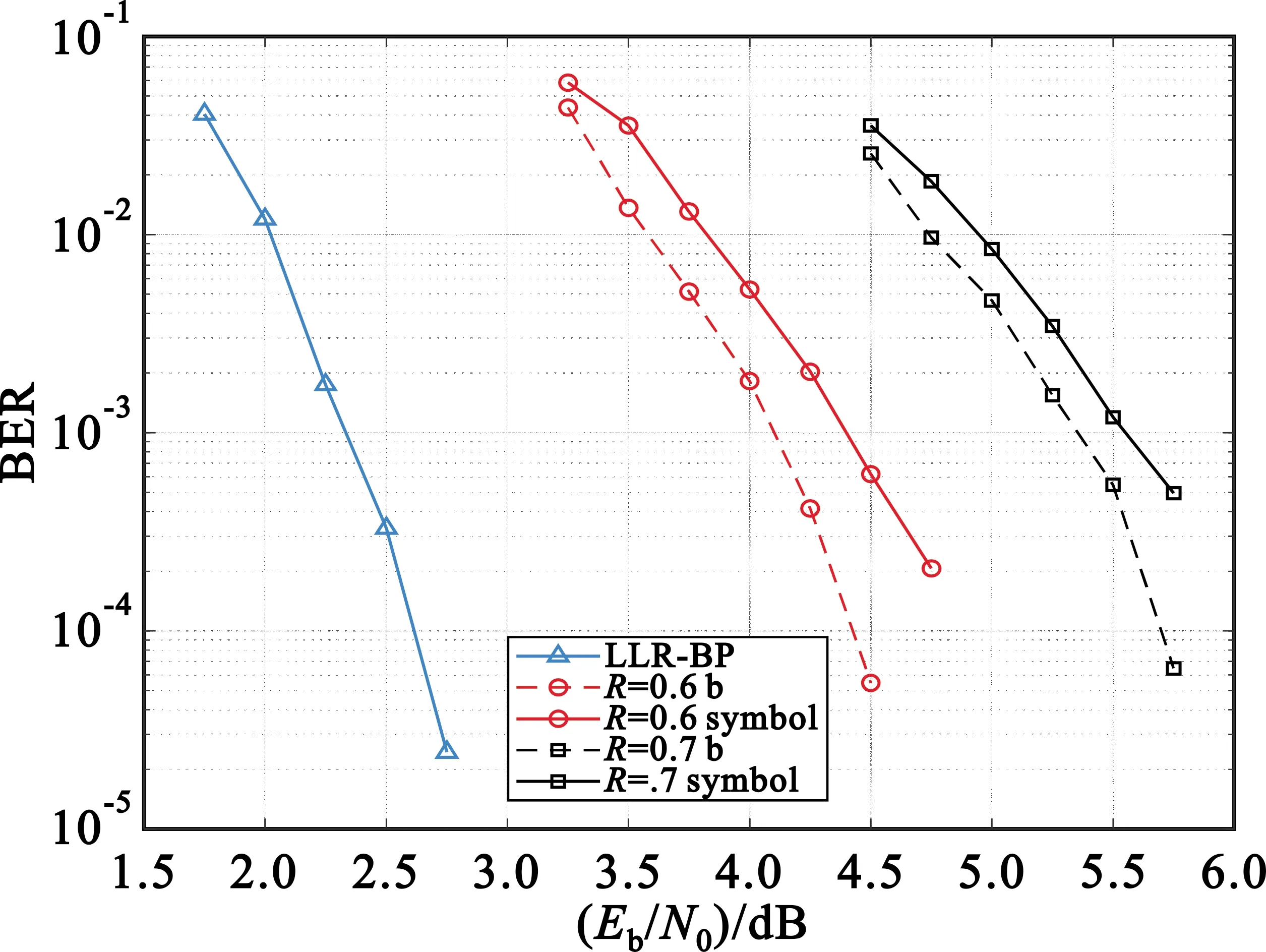
图7 576码长打孔对比图

图8给出了本文算法与文献[10]中的基于环路的符号级打孔算法和传统符号级打孔算法的对比，母码码率为0.5，采用BPSK调制，打孔后码率都增加到0.6和0.7。两组数据中在低信噪比区域时，比特级新打孔算法与基于环路的符号级打孔算法译码性能差异不大，几乎持平，但随着信噪比的增大，本文的新算法在10-4量级时拥有了0.2 dB的增益，性能良好。

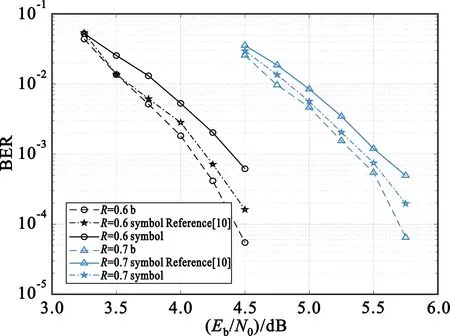
图8 比特级与符号级打孔对比图

综上所述，多元比特级新型打孔算法有比多元常规符号级打孔算法更佳的性能，在各码率都获得了一定的增益。

5 结束语

本文基于二进制镜像理论提出了一种比特级的多元码率兼容LDPC码打孔算法，通过对多元矩阵进行二进制镜像处理，再根据度分布选取合适的比特打孔节点，将打孔范围从符号级扩展到比特级，实现了码率由低到高的转变。仿真结果表明，本文所提出的新型比特级打孔算法相较于传统的符号级打孔算法，译码性能显著提高，为通信系统中信息的传输提供了可靠性和有效性。比特级打孔节点的选择不仅仅局限于度分布，未来研究可考虑恢复树或环路对译码性能的影响。