协作D2D异构网络的联合资源分配和功率控制*
高寿斌,张 远,万 兵
(1.恩施职业技术学院 信息工程学院,湖北 恩施 445000;2.山东理工职业学院 软件工程学院,山东 济宁 272067;3.重庆水利电力职业技术学院 智能制造学院,重庆 404100)
0 引 言
当前,通信网络对数据传输速率、能效及局域服务的需求不断增长,常规蜂窝网络的访问模式已无法满足日益增长的通信需求,因此迫切需要第五代(5G)移动通信技术对通信模式进行转换。其中,设备到设备(Device-to-Device,D2D)的通信是实现通信模式转换的一项重要技术。
D2D技术能够实现D2D用户(D2D Users,DU)之间的直接通信,无需基站(Base Station,BS)处理,从而有效提高蜂窝网络的频谱效率,减少BS负载,并提升网络中边缘用户的服务质量[1]。但D2D通信技术也存在着DU对复用蜂窝用户(Cellular Users,CU)干扰的问题[2]。因此,设计用于保证网络通信质量的干扰控制策略是D2D通信的核心方法,国内外众多学者对此进行了大量研究。文献[3]针对网络功率分配、准入控制和模式选择开展研究,提出了一种具有干扰约束的外部逼近解决办法。文献[4]提出了一种基于粒子群优化(Particle Swarm Optimization,PSO)的信道分配和功率控制方案,得到最大化整体网络吞吐量。文献[5]通过研究D2D网络中的无线电资源分配、模式选择和功率协调需求,实现更高的网络吞吐量。但上述传统资源分配方法存在长距离衰落缺陷,难以满足边缘用户的服务质量(Quality of Service,QoS)需求。文献[6]基于二分匹配理论,提出了一种中继选择和资源分配方案,仿真表明该方法在运行时间和平均效用方面具有良好性能。文献[7]运用空闲的Femtocell基站充当D2D传输对的中继,设计了一种底层D2D网络的功率分配和中继选择方案。但上述两种方案仅研究了小规模中继选择场景,在实际密集规模的DU场景中适应性较差。
综上,现有研究内容已取得良好成果,但尚未充分考虑密集CU和DU场景下的功率控制、资源分配和多个中继选择的情况,限制了实际系统的应用范围;其次,将资源分配转换为凸优化问题,需要大量复杂的数学推导或学习机制,缺乏良好的通用性。因此,为突破现有模型的局限性,本文提出了一种用于联合资源分配和功率控制的新型量子珊瑚礁优化算法(Quantum Coral Reef Optimization Algorithm,QCROA)。首先构建了一种协作的D2D通信机制的融合数字家庭网络模型(Convergent Digital Home Network,CDHN),使得DU共享CU的频谱资源块(Spectrum Resource Block,SRB);通过选择位于蜂窝网络中的IU作为中继,完成信息传输,得到模型总吞吐量的解析公式。仿真和实验验证了所提算法的正确性和有效性。
1 CDHN系统模型与吞吐量分析
CDHN网络由1个BS、M个CU、N个DU、D个闲置用户(Idle Users,IU)组成,如图1所示。其中,CU的数字顺序表示为ψ= {1,2,…,M},DU的数字顺序表示为τ= {1,2,…,N},IU的数字顺序表示为κ= {1,2,…,D}。每个DU传输对由一个DU发送器(D2D Users Transmitter,DUT)和一个DU接收器(D2D Users Receiver,DUR)组成。在信息流转过程中,BS向CU发送信息,并以IU作为中继,协助CDHN中DU的信息传输。每个DUT-DUR对选择一个IU完成传输,且IU对信息重新编码,并将信息发送到DUR。
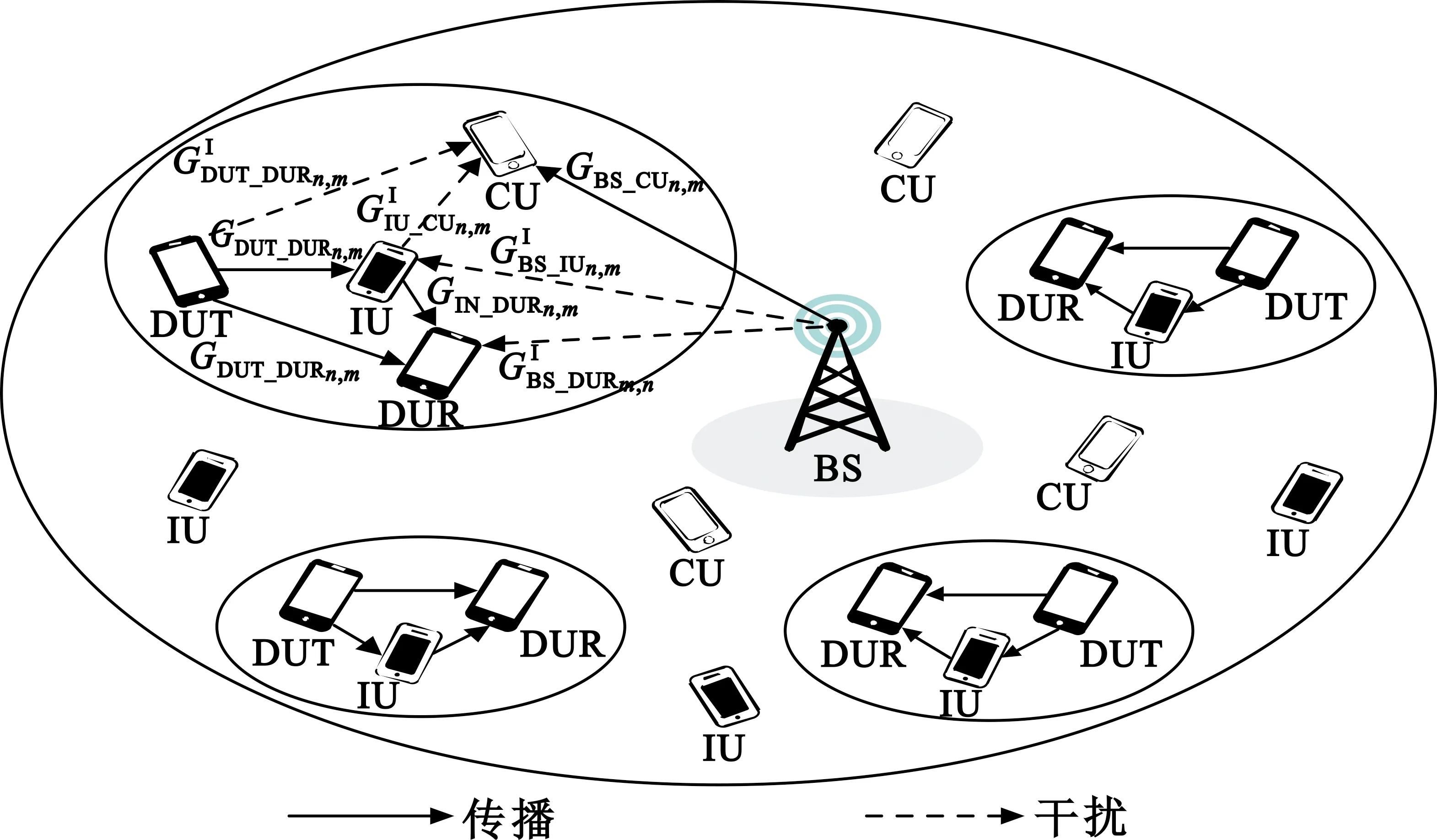
图1 CDHN系统模型
通常,两个节点之间的传输信道增益(Transmission Channel Gain,TCG)在一个时隙中保持不变,且TCG在两个不同的时隙中彼此独立。假设CU的SRB分配方案是预先确定的,且CU的每个下行SRB由一个DU进行共享,则SRB分配约束公式如式(1)所示[2]:
(1)

在下行链路CDHN中,BS将信息发送到CU。同时,各DU分别传输信息,其信息传输过程包含以下两个步骤:DUT将信号传输到DUR及其对应的IU,IU解码接收信号;IU将解码后的信号发送到DUR,通过最大比对DUT和IU的信号进行合并。
若两个步骤的时间长度相等,所选的IU将共享其对应的DU传输对的SRB,以完成通信。因此,其信号干扰噪声比(Signal-to-Interference pluse Noise Ratio,SINR)表示为[2]
(2)
式中:PDUT_DURn,m表示第m个SRB上的第n个DUT的传输功率,PBS_CUm表示从BS到第m个CU的传输功率,η0是高斯白噪功率。
第n个DUT到第m个SRB的相应IU链路的SINR如式(3)所示:

(3)
对于CDHN的第m个CU,其SINR如式(4)所示:
(4)
第二步中,由IU向DUR传输信号,第n个IU至第m个SRB的DUR链路表示如下:

(5)
式中:PIU_DURn,m表示第m个SRB上第n个IU的传输功率。对于DF传输协议,第n个DU传输对的吞吐量为
rDUT_DURn,m=
(6)
令RDUn表示第n个DU的吞吐量,则

lb(1+γDUT_DURn,m+γIU_DURn,m)},∀n∈τ。
(7)
因此,DU的总吞吐量为
(8)
则第二步中第m个CU的SINR如式(9)所示:
(9)
CDHN中所有CU的总吞吐量RCU为
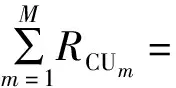
(10)
由式(8)和式(10)可得CDHN的总吞吐量,如式(11)所示:
Rtotal=RCU+RDU=
(11)
因此,在保证QoS的前提下,需研究SRB分配、IU选择及传输功率控制的联合优化,以最大化DU和CU链接的总吞吐量,如式(12b)所示:
maximizeRtotal(b,s,PBS_CU,PDUT_DUR,PIU_DUR)=
(12a)
(12b)
(12c)
sm≠sj,∀m≠J,
(12d)
(12e)

2 基于QCROA的联合资源分配与功率控制
2.1 QCROA最佳化
本文结合传统珊瑚礁优化算法(Coral Reef Optimization Algorithm,CROA)和量子进化的优点,提出QCROA算法,即在一个I维空间中,存在一个由H个量子珊瑚组成的量子珊瑚礁,每个量子珊瑚由I个量子位组成。第t次迭代中的第h个(h= 1,2,…,H)量子珊瑚如式(13)所示:
(13)

(14)

(15)
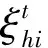


(16)
(17)

(18)
由式(18),根据其健康程度对量子珊瑚进行分类,健康度最高的顶级ρ2×H量子珊瑚将继续无性繁殖,并复制ρ2×H量子珊瑚,ρ2为无性繁殖率。其中,复制的量子珊瑚将淘汰量子珊瑚礁中最弱的ρ2×H量子珊瑚。最后,根据当前迭代的最佳量子珊瑚生成全局最优量子珊瑚。
2.2 QCROA分析
算法的收敛性是重要的算法性能评价指标,QCROA算法可利用量子演化机制(即有性生殖、无性生殖和掠夺)来获得最佳解。一方面,外部有性生殖进化策略能够提高QCROA的收敛速度和收敛精度;另一方面,内部有性生殖、无性生殖和贬低进化策略能够有效增加多样性。现对QCROA进行收敛性分析和复杂性计算。
命题1:Xt是第t次迭代的总体测量状态,将QCROA的种群搜索序列定义为{Xt;t>0},其中,{Xt;t>0}是有限的二次马尔科夫链。
证明:假设每个量子珊瑚的长度为I,QCROA的种群大小为H。由于每个量子珊瑚的量子位的测量状态为{0,1},因此Xt的状态空间大小为2I×H。同时,QCROA的群序列为有限序列。此外,QCROA的有性生殖、无性生殖和折旧过程与t无关,Xt+1仅与t有关。因此,{Xt;t>0}是有限的次级马尔科夫链。
命题2:QCROA以1的概率收敛到全局最优。
证明:定义QCROA的状态空间为S={S1,S2,…,S2I×H},最优解的状态集为P。在第t次迭代中,量子珊瑚种群处于状态Sv(v=1,2,…,2I×H)的概率表示为PSv(t),Sv(t)为量子珊瑚种群的第t次迭代状态。将Pt定义为量子珊瑚种群在第t次迭代中不属于P的概率,则根据马尔科夫链和命题1得到[2]:

(19)
式中:PSvSj(t)是量子珊瑚种群在第t次迭代中的转移概率。
马尔科夫链展开为
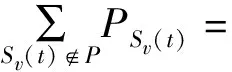
(20)
变换可得
(21)
结合命题1、式(19)、式(21)可得
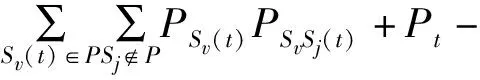
(22)
由于在有性生殖、无性生殖和掠夺过程之后的迭代中生成最优量子珊瑚,因此,根据概率统计性质和式(22)可得
0≤Pt+1 (23) (24) 利用有性生殖、无性生殖和掠夺进化方法,可以将量子珊瑚种群视为大规模的迭代过程,如式(25)所示: (25) 因此,QCROA以1的概率收敛到全局最优。 命题3:运行t次迭代后,QCROA的计算复杂度为O(t×H×(3I+ρ2+2))。 证明:如第2.1节所述,对于外部有性生殖和内部有性生殖的过程,QCROA需要在每次迭代中生成量子珊瑚的量子旋转角和量子比特,其计算复杂度为O(2×H×I)。其中,量子珊瑚的测量采用式(15)获得,计算复杂度为O(H×I)。当生成每个量子珊瑚和全局最优量子珊瑚时,计算复杂度为O(2H)。对于QCROA的无性生殖和掠夺过程,其计算复杂度为O(ρ2×H)。由此可知,QCROA在运行t次迭代后的计算复杂度为 O(t(3×H×I+ρ2×H+2H))=O(t×H×(3I+ρ2+2))。 (26) QCROA方法可优化CDHN的资源分配和功率控制。利用适应度函数可计算第h个量子珊瑚的健康度。量子珊瑚礁中,每一个量子珊瑚的测量状态都对应于需要优化的参数向量。本文所提出的资源分配和功率控制问题,需要优化的参数向量为[b,s,PBS_CU,PDUT_DUR,PIU_DUR]。 通过改变参数向量,优化其他系统参数。对于资源分配和功率控制,将每个用户的发射功率和IU选择的数字顺序,根据二进制位进行编码。因此,将寻找最优联合资源分配和功率控制方案的复杂工程问题转化为寻找全局最优量子珊瑚测量状态的优化问题。全局最优量子珊瑚的测量状态,对应于最优联合资源分配和功率控制方案。 为验证QCROS算法的性能,在Windows7环境下利用Matlab2013a进行仿真实验。假设DUT-DUR对、IU和CU在CDHN中随机分布,CDHN的半径为500 m。TCG和ICG遵循指数分布,参数d-l(d是任意两个节点之间的距离)和l是路径损耗指数。为保持通用性,令BS到每个CU的最大传输功率等于到每个DU传输对的最大传输功率。所有仿真结果均为100次试验的平均值。表1所示为仿真参数。 表1 仿真参数 针对QCROA与CROA、基于教学的优化(TLBO)、离散粒子群优化(DPSO)、正余弦算法(SCA)、差分进化算法(DEA)、最大功率随机资源选择方案(MPRRS)和半功率随机资源选择方案(HPRRS)的性能进行比较。其中,离散智能算法QCROA和DPSO,分别用10个二进制位和6个二进制位,对各用户的发射功率和各IU选的数字顺序进行编码。连续智能算法,即CROA、TLBO、SCA和DEA,在优化SRB分配时,将连续变量舍入为整数。MPRRS算法采用最大传输功率传输每个节点的信息,而SRB分配和IU选择方案则采用随机方式。在HPRRS中,每个节点以半最大功率进行信息传输,SRB分配和IU选择采用随机选择。QCROA、CROA、TLBO、DPSO、SCA、DEA、MPRRS和HPRRS的最大迭代次数为2 000次,总体规模为60次。本文所提QCROA算法,设c1=0.4,c2=0.1,ρ1=0.9,ρ2=1/12。 图2所示为QCROA、CROA、TLBO、DPSO、SCA、DEA、MPRRS和HPRRS方案的总吞吐量收敛性能。由图可知,QCROA算法可获得更高的总吞吐量。QCROA具有较快的收敛速度,在迭代次数达到1 500次时收敛到全局最优。由此可知,QCROA的收敛速度比CROA、TLBO、DPSO、SCA、MPRRS和HPRRS方案快。当迭代次数达到150次时,DEA快速收敛到局部最优,但不能逃离局部最优,从而陷入局部收敛,无法得到全局最优。而QCROA结合了量子演化理论和CROA的优点,通过内部有性生殖进化机制提高整个种群的收敛速度,通过外部有性生殖进化方式增加种群多样性。此外,无性繁殖机制可快速去除有害量子珊瑚。 图2 收敛性比较 因此,QCROA的收敛速度和种群多样性均优于其他基于智能优化算法的方案,能够跳出局部最优,得到吞吐量最高的全局最优。由于QCROA在迭代次数达到1 500次时收敛,为简化仿真过程,后续仿真中设置最大迭代次数设为1 500次。 图3 不同的总吞吐量性能比较 图4所示为不同CU数量下的各算法总吞吐量。由图可知,在仿真过程中,CU的数量从10到40不等,所有算法的CDHN总吞吐量均随CU数的增加而增加,在保证用户服务质量的前提下,QCROA比CROA、TLBO、DPSO、SCA、DEA、MPRRS和HPRRS具有更高的吞吐率。 图4 不同CU数量下总吞吐量的性能比较 图5 不同的总吞吐量性能比较 图6所示为不同IU数的性能比较,IU的数目从10到35不等。对于不同的IU数目,QCROA可获得比CROA、TLBO、DPSO、SCA、DEA、MPRRS和HPRRS更好的性能,总吞吐量随着IU数目的增加而增加,更多的信息单元能够为数据单元的信息传输提供更多的选择。因此,当IU数增加时,不同方案的总吞吐量将变大。由此,由上述分析可知,在不同仿真情况下,QCROA均可获得最佳性能。 图6 不同IU数下总吞吐量的性能比较 图7 不同和CU数的总吞吐量 图8 不同和IU数的总吞吐量 图9 不同和CU数的总吞吐量 图10 不同和的总吞吐量 针对下行CDHN中的最优资源分配和功率控制问题,本文推导了CDHN的总吞吐量表达式,并提出了一种新型的QCROA算法。通过分析与仿真得出以下结论: (1)QCROA算法具有较快的收敛速度,在迭代次数达到1 500次时收敛到全局最优; (2)QCROA算法的收敛速度和种群多样性均优于其他基于智能优化算法的方案,并能够跳出局部最优,得到吞吐量最高的全局最优; 本算法尚未应用到具有超密集节点异构性和集群机制的场景中,由此后续还需要进行更深层次的研究。2.3 QCROA联合资源分配与功率控制过程
3 算法仿真与分析

3.1 QCROA的仿真性能比较
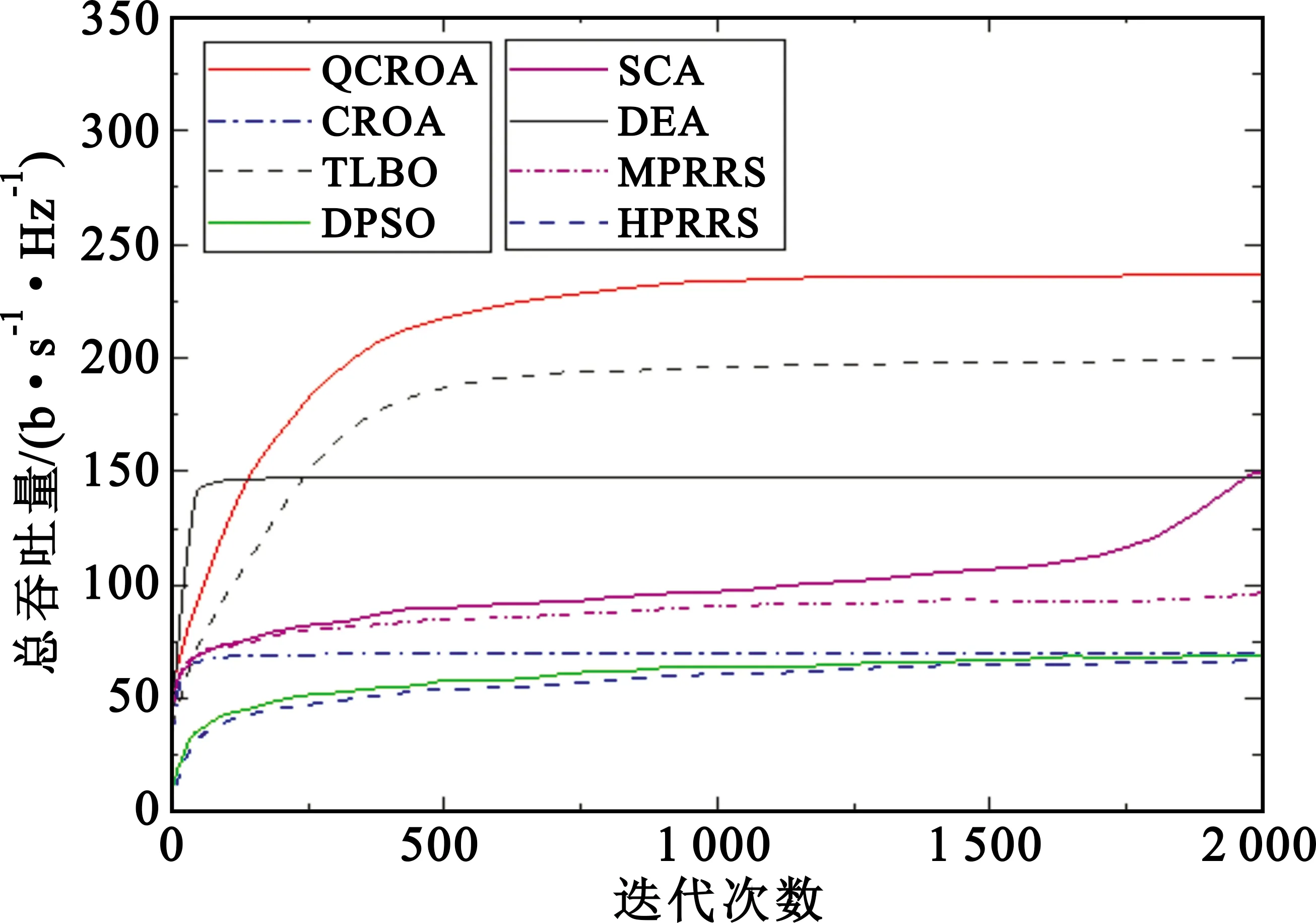






3.2 不同参数对CDHN的影响





4 结束语

