考虑延迟的线控转向二自由度内模控制

杜文龙 陈 俐 刘文通 陈 峻

1.上海交通大学动力装置与自动化研究所，上海，2002402.上海交通大学海洋工程国家重点实验室，上海，200240

0 引言

线控转向技术是自动驾驶汽车实现路径跟踪与避障避险的关键技术之一。与传统汽车转向系统不同，线控转向系统取消了从转向盘到转向车轮的机械连接，使用转向电机控制车轮转角，具有结构紧凑、布置方案灵活且更易于实现集成控制等优点[1-2]。

线控转向控制须快速、高精度地实现期望车轮转角，但是，由于信号传输、转向执行器的机械间隙、摩擦等原因，线控转向系统存在响应延迟。延迟使得控制系统的调节时间变长，超调量增大，严重时引起振荡甚至失稳[3]。为了改善线控转向系统的动态性能，有必要设计对延迟具有补偿效果的控制策略。

近年来，线控转向系统中的延迟问题逐渐引起关注。文献[4]的研究表明，网络传输延迟超过一个通信周期的概率大于10%将引起线控转向系统功能失效；文献[5]研究发现，当延迟大于50 ms时采用比例微分控制的研究线控转向系统失稳。为了消除延迟对线控转向系统转角跟踪性能的影响，文献[6]针对转向系统的信号传输和执行器响应延迟，提出了线性矩阵不等式镇定方法，仿真表明镇定性能得到改善，但是该文献并未提及跟踪性能。文献[7]限定通信延迟的大小和变化率的边界值，研究了鲁棒模糊控制策略，给出了以线性矩阵不等式描述的鲁棒跟踪稳定条件，但求解计算量较大。

本文提出基于二自由度内模控制方法进行线控转向系统转角跟踪。内模控制具有对偶稳定性、理想控制器特性和零稳态偏差特性[8-10]，对模型误差具有一定鲁棒性，能较好地减小延迟的影响。二自由度内模控制可独立设计跟踪回路与抗干扰回路，提高受复杂工况干扰影响的系统跟踪精度[10]，但是，延迟是非线性环节，这给二自由度内模控制的实施带来困难。跟踪控制器和抗干扰控制器分别由逆控制器和滤波器组成，而逆控制器的求解需要对被控对象的名义模型进行求逆，据此设计滤波器，延迟环节将会给逆控制器和滤波器的设计带来不便。因此，一些研究建立的名义模型不包含延迟环节[11-12]，但是当延迟较大时模型误差增大，导致跟踪精度降低。

将延迟环节线性化，便于求逆并使逆控制器可实现，可克服非线性环节带来的内模控制器设计障碍。延迟环节的线性化方法主要有Padé近似、Taylor近似和全极点近似三种。Padé近似在相同近似阶数下精度较高，但是Padé近似产生右半平面零点，从而出现非最小相位部分，为了保证系统内部稳定，往往需要舍弃非最小相位部分，这反而降低了控制器精度[13]。Taylor近似也产生右半平面零点，求解逆控制器时将全部被舍弃，相当于未考虑延迟。全极点近似是将延迟环节的分母部分进行Taylor展开[14]，这种形式可避免产生右半平面零点，不会出现非最小相位部分，可直接用于逆控制器的求解。本文采用全极点近似，该方法尚未用于内模控制器的求解。

本文首先将延迟模型与线控转向系统模型相结合，构建新的名义模型，然后采用全极点近似方法将延迟环节线性化，在此基础上设计二自由度内模控制框架中的跟踪控制器和抗干扰控制器，之后开展稳定性分析，得到满足稳定条件的滤波器参数设计准则。通过MATLAB/Simulink仿真给出不同延迟作用下的转角跟踪性能，并与名义模型不含延迟环节的内模控制以及经典PID控制分别进行比较。在二自由度内模控制框架下，比较三种延迟线性化方法(全极点近似、Taylor近似和Padé近似)的跟踪误差随延迟量变化的规律。最后开展线控转向系统台架试验，分别以斜坡、正弦和变频率信号为参考输入，比较采用不同控制方法的线控转向系统跟踪性能。

1 系统建模

在线控转向系统中，转向执行机构接收线控转向系统控制器发出的指令并执行，实现转向轮预期转角。从控制器发出指令到转向执行机构开始执行该指令之间，由于通信、转向执行机构摩擦、间隙和传感器信号处理等因素而产生响应延迟。本节分别建立转向执行机构模型和延迟环节模型，二者组成被控对象模型。

1.1 转向执行机构建模

转向执行机构的物理模型如图1所示，主要由转向电机、减速器、齿轮齿条转向器、转向梯形机构组成。

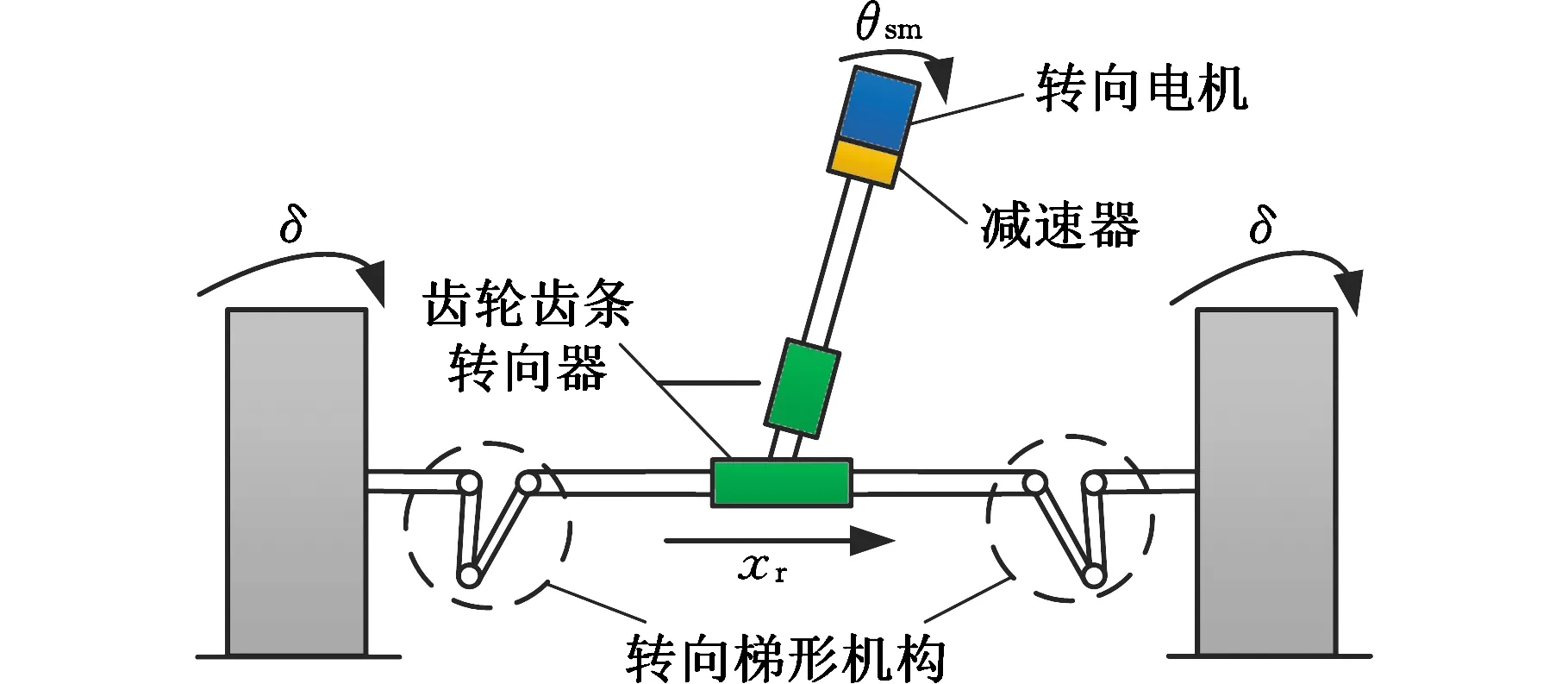
图1 转向执行机构物理模型

转向执行机构的动力学方程为[15]

(1)

式中，Mr为转向执行机构的等效质量；Br为转向执行机构的等效阻尼系数；xr为齿轮齿条转向器齿条的位移；Fc为库仑摩擦力；Fs为回正力；Keq为电机电流到控制输入力的等效比例系数；ism为电机电流。

库仑摩擦力Fc和回正力Fs的计算公式为[15]

(2)

Fs=ρftanh(δ)/Ls

(3)

式中，ξf为库仑摩擦力矩常量；ρf为回正力矩系数；Ls为转向梯形机构的等效力臂；δ为前轮转角。

将式(3)代入式(1)，并采用双曲正切函数的线性近似(tanh(δ)≈δ)，可得

(4)

令前轮转角δ与齿条位移xr的比例系数

K0=δ/xr

(5)

由式(4)、式(5)推导可得

(6)

以电机电流ism(s)为控制输入，以库仑摩擦力Fc(s)为干扰输入，以前轮转角δ(s)为系统输出，将式(6)写成传递函数形式：

δ(s)=Gi(s)ism(s)+GF(s)Fc(s)

(7)

(8)

1.2 延迟环节建模

延迟τ使得转向电机电流指令被延迟执行。令转向电机控制器发出的电流指令为ic，式(1)中转向电机电流ism表达式为

ism(t)=ic(t-τ)

(9)

其传递函数为

Gd(s)=ism(s)/ic(s)=e-τs

(10)

2 控制器设计

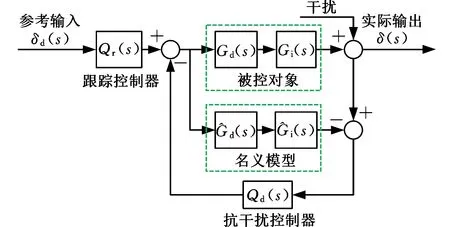
图2 考虑延迟的二自由度内模控制框图

D(s)=GF(s)Fc(s)

(11)

该结构中，Qr(s)为跟踪控制器，Qd(s)为抗干扰控制器。

在图2所示的闭环控制系统中，实际输出δ(s)计算公式为

δ(s)=

(12)

将被控对象传递函数写为

M(s)=Gi(s)Gd(s)

(13)

假设名义模型与实际模型匹配，则

(14)

将式(13)和式(14)代入式(12)可得

δ(s)=Qr(s)M(s)δd(s)+(1-Qd(s)M(s))D(s)

(15)

由式(15)可见，跟踪控制器Qr(s)与抗干扰控制器Qd(s)共同决定系统输出δ(s)，并且Qr(s)与Qd(s)相互独立，可以单独设计。

应用一阶全极点近似方法[14]对延迟模型式(10)进行线性化，即

Gd(s)=1/eτs≈1/(τs+1)

(16)

由式(8)可知，Gi(s)无右半平面零点或极点。将式(16)代入式(13)，可得被控对象最小相位部分传递函数：

(17)

2.1 跟踪控制器

考虑无干扰情况，设计跟踪控制器Qr(s)。令D(s)=0，则式(15)可写为

δ(s)=Qr(s)M(s)δd(s)

(18)

跟踪控制的目标为

δ(s)=δd(s)

(19)

为了实现跟踪控制目标，将式(19)代入式(18)，可得

Qr(s)M(s)=1

(20)

为了保证控制系统稳定，对被控对象最小相位传递函数M-(s)求逆，并引入低通滤波器Fr(s)[10]，以保证控制器可实现。设计跟踪控制器Qr(s)如下：

(21)

低通滤波器Fr(s)按下式设计：

(22)

其中，参数λr用于调节跟踪控制性能，n为正整数，用于补偿控制器Qr(s)中相对阶，从而使系统可实现。当滤波器参数λr较小时，Fr(s)趋于1，则等式(20)近似成立，从而实现跟踪目标。

2.2 抗干扰控制器

为了抑制外界干扰D(s)对转角跟踪的影响，式(15)须满足

1-Qd(s)M(s)=0

(23)

类似地，对被控对象最小相位传递函数M-(s)求逆，并引入低通滤波器Fd(s)，抗干扰控制器Qd(s)可设计如下：

(24)

低通滤波器Fd(s)按下式设计：

(25)

其中，参数λd用于调节抗干扰控制器性能，m为正整数，用于补偿抗干扰控制器Qd(s)的相对阶，从而使系统可实现。当滤波器参数λd较小时，Fd(s)趋于1，则等式(23)近似成立，从而实现抗干扰目标。

3 稳定性分析

本节通过稳定性分析，给出二自由度内模控制下线控转向系统的闭环稳定条件。

由式(15)可知，从参考输入δd(s)到前轮转角δ(s)的闭环传递函数为

T1(s)=Qr(s)M(s)

(26)

将式(13)、式(16)、式(21)和式(22)代入式(26)得

(27)

可见，如果λr>0，则闭环传递函数T1(s)的极点实部为负，因此，T1(s)闭环稳定的充要条件为λr>0。

类似地，根据式(15)，从外界干扰D(s)到前轮转角δ(s)间的闭环传递函数为

T2(s)=1-Qd(s)Gi(s)e-τs

(28)

将式(16)、式(24)和式(25)代入式(28)得

(29)

可见，如果λd>0，则闭环传递函数T2(s)的极点实部为负，因此，T2(s)闭环稳定的充要条件为λd>0。

4 结果与分析

4.1 延迟量对跟踪性能的影响

在MATLAB/Simulink软件中开展不同延迟时间作用下线控转向系统的转角跟踪仿真，从稳定性和跟踪误差两方面研究延迟量对跟踪性能的影响。为了说明在内模控制的名义模型中包含延迟模型的必要性，给出名义模型中含延迟模型的二自由度内模控制与名义模型中未含延迟模型的二自由度内模控制的结果比较。同时，作为比较，也给出了经典PID控制的跟踪性能。

从以荣威E550车型为原型搭建的线控转向试验台架系统获取仿真参数，整车参数如表1所示，线控转向执行机构参数如表2所示。线控转向系统模型式(6)中回正力矩系数ρf根据CarSIM软件的整车模型和整车参数得到[16]。

表1 车辆模型参数

表2 转向执行机构参数

整车回正力矩FsLs按下式计算[16]：

(30)

(31)

式中，β、γ分别为汽车的质心侧偏角和横摆角速度。

将表1中的参数值代入式(30)和式(31)，结合整车模型的输出，得到回正力矩FsLs，代入式(3)，计算可得回正力矩系数ρf为150。

本文提出的二自由度内模控制(简称“2DOF IMC”)中名义模型包含延迟环节，仿真结果以IMC_d表示，与之比较，不含延迟环节的2DOF IMC名义模型的仿真结果以IMC_nd表示，经典PID控制的仿真结果以PID表示。

名义模型包含延迟环节的2DOF IMC的跟踪控制器按式(21)设计，抗干扰控制器按式(24)设计。滤波器阶数取值m=3、n=3，使控制器相对阶为零，滤波器参数λr=0.0055、λd=0.4。

名义模型不包含延迟环节的2DOF IMC的跟踪控制器的表达式与式(21)相比较，缺少延迟项τs+1；类似地，抗干扰控制器的表达式与式(24)相比较，也缺少延迟项τs+1。滤波器阶数取值m=2、n=2，使控制器相对阶为零。滤波器参数的最优取值为λr=0.0005、λd=0.5。

经典PID控制器参数的最优取值如下：比例增益系数为42.48、积分增益系数为507.4、微分增益系数为0，滤波器参数N=100。

延迟τ=90 ms的仿真结果如图3所示。由图3b可见，名义模型含延迟的2DOF IMC的最大跟踪误差最小，约为0.024 rad；名义模型不含延迟的2DOF IMC的最大跟踪误差约为0.037 rad，PID控制的最大跟踪误差约为0.046 rad。用转角跟踪过程的平均跟踪误差进行评价，名义模型含延迟的2DOF IMC约为0.0044 rad，而名义模型不含延迟的2DOF IMC约为0.0106 rad，PID的平均跟踪误差约为0.0074 rad。0～1 s，跟踪斜坡参考输入过程中，名义模型含延迟的2DOF IMC未发生抖动，且跟踪误差保持在较小的范围内，而PID控制在跟踪过程中均发生了一定的抖动。另外，名义模型不含延迟的2DOF IMC在2～5 s过程中出现了较大的稳态误差，约为-0.0070 rad。这是由于名义模型未考虑延迟环节，与实际模型不匹配，因而导致较大误差。

(a)跟踪结果

延迟量对平均跟踪误差的影响如图4所示。统计0～5 s的平均跟踪误差，总体上，名义模型含延迟的2DOF IMC的平均跟踪误差几乎不受延迟量变化的影响，PID的平均跟踪误差受到一定影响，而名义模型不含延迟的2DOF IMC的跟踪误差随着延迟量增大显著增大。当延迟时间为30 ms时，名义模型含延迟与不含延迟的2DOF IMC的平均跟踪误差近似相等，PID的平均跟踪误差大于两种2DOF IMC，因此，为了简化控制器算法并兼顾跟踪精度，此时可以采用不含延迟的名义模型设计2DOF IMC控制器。随着延迟量增大，由于三个控制方法的控制参数均是在延迟时间为90 ms下调校的，因此名义模型含延迟的2DOF IMC的平均跟踪误差先减小后增大，但是增大幅度很小，对延迟量的变化不敏感；另外两个控制方法的平均跟踪误差随延迟量增大均逐渐增大。因此，当延迟量较大时，采用含延迟的2DOF IMC，线控转向系统可获得较好的转角跟踪性能。

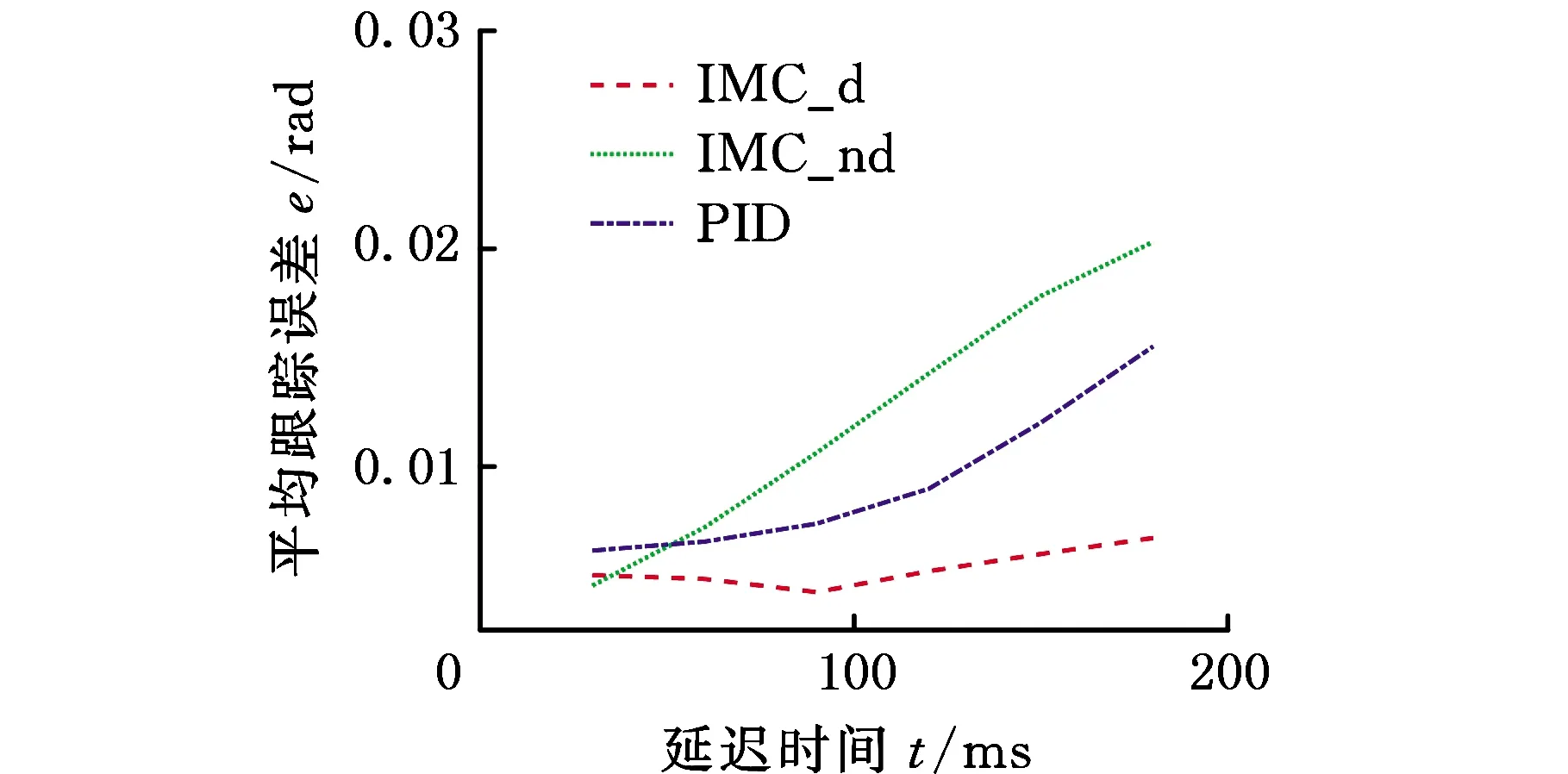
图4 延迟量对平均跟踪误差的影响

4.2 延迟环节线性化方法对跟踪性能的影响

目前对纯延迟环节的近似方法主要有全极点近似、Taylor近似和Padé近似[14]，它们的一阶形式较为常用，相应表达式如表3所示。在图3所示的参考输入下，比较采用这三种近似方法的2DOF IMC控制器的跟踪性能。

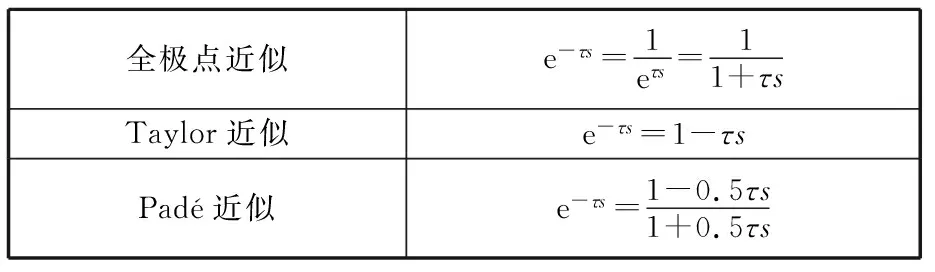
表3 延迟环节不同近似方法

采用三种近似方法的控制框图相同，如图2所示。三者的区别在于控制器Qr(s)与Qd(s)的形式。表4给出了三种控制器的推导结果以及调试得到的滤波器参数最优取值。

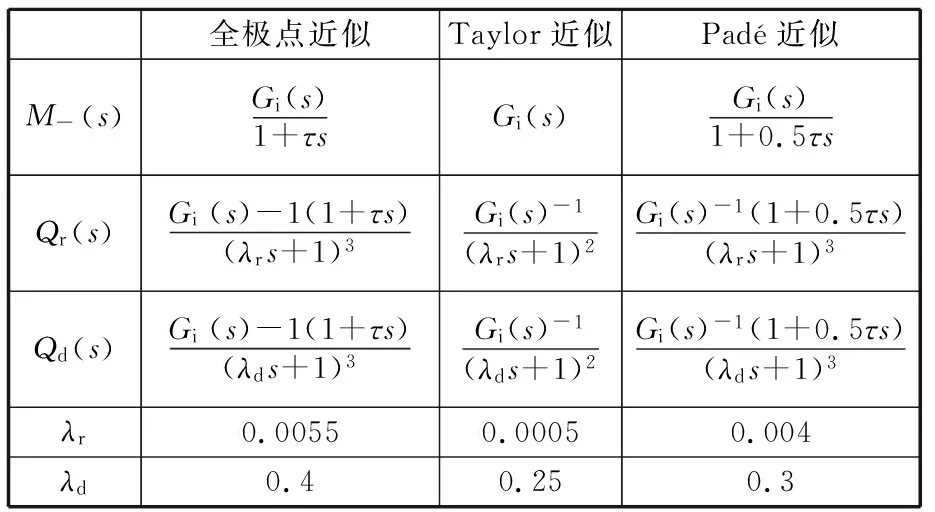
表4 不同近似方法下的设计结果

由表4可知，Taylor近似的延迟项由于产生非最小相位项被舍弃，因此在控制器Qr(s)、Qd(s)中无延迟项τ，虽然能保证系统稳定，但跟踪精度对延迟的适应性受到限制。采用Padé近似方法，控制器中舍弃了非最小相位部分，与全极点近似控制器相比较，其分子中一阶微分环节的时间常数减半，因此跟踪精度仍将有所降低。全极点近似不存在非最小相位部分，因此控制器形式最完整，跟踪精度最高。图5所示的仿真结果验证了该分析。

(a)跟踪结果

图5中，输入为图3所示的参考输入，延迟为90 ms，全极点近似方法的最大跟踪误差最小，为0.024 rad，Padé近似方法的最大跟踪误差约为0.031 rad，Taylor近似方法的最大跟踪误差较大，约为0.037 rad。此外，0～5 s的过程中，全极点近似的平均跟踪误差最小，为0.0044 rad，Padé近似的平均跟踪误差为0.0056 rad，而Taylor近似的平均跟踪误差最大，约为0.0061 rad。

采用三种延迟近似方法时延迟量对平均跟踪误差的影响如图6所示，可见，总体上，全极点近似方法受延迟量的影响相对其他两种近似方法较小。全极点近似方法随延迟量的变化规律与图4中的相同，由于控制器参数均是在时间延迟为90 ms时调校，因此越接近90 ms，跟踪误差越小，反之，越大。因此，当延迟量小于50 ms时，全极点近似方法的误差比其他两种方法的略大，但是随着延迟量的增大，Taylor和Padé近似方法的误差增长较快，而全极点近似方法的误差相对平稳。

图6 采用三种近似方法的平均跟踪误差曲线

综上，当延迟量小于50 ms时，可以采用Taylor近似求解2DOF IMC的控制器，当延迟时间大于50 ms时，为了获得较小的转角跟踪误差，宜采用全极点近似求解2DOF IMC控制器。

4.3 台架试验验证

线控转向试验台架的整体框架如图7所示。图7中，转向盘用于直接接收驾驶员转向指令；转向电机和反馈电机均为直流无刷伺服电机，分别用于控制转向和模拟路感；车轮的转向阻力由磁粉制动器模拟，大小可控。减速器输出轴和齿轮齿条转向器的齿轮之间利用万向节连接，磁粉制动器的输出轴同样使用万向节与阻力加载齿轮齿条机构连接。齿轮齿条转向器的齿条和阻力加载齿轮齿条机构的齿条利用法兰盘连接。齿条位移xr由位移传感器测得，将齿条位移代入式(5)，可求得前轮转角δ。dSPACE PX10为控制器原型，能够接收各个传感器信号并发送控制信号给各个设备，转角跟踪的参考输入信号由控制器原型生成。

1.转向盘 2.扭矩传感器和转角传感器 3.路感电机 4.转向电机 5.齿轮齿条转向器 6.位移传感器 7.拉压力传感器 8.磁粉制动器

试验中，以M序列电流方波为输入，前轮转角为输出，采用MATLAB中System Identification应用程序对不含轮胎的转向执行机构的参数进行离线辨识。

按照二阶系统结构对系统参数进行辨识，得到Mr=10 kg，Br=297.4 N·s/m，Keq=6.192 N/A，τ=45 ms，即不含轮胎的转向执行机构的传递函数为

(32)

模型结果与试验结果的比较如图8所示，可见，在M序列电流方波输入下，模型结果与试验结果比较吻合。

(a)M序列电流(输入)

式(32)说明试验台架存在45 ms延迟，即从系统发出电流指令到开始响应产生运动的时间差，反映了台架本身间隙、摩擦、数据采集以及与位移传感器连接的硬件滤波器引起的延迟。在控制器试验中，由于位移传感器信号存在噪声，需要采用低通滤波器进行平滑，故带来的延迟约35 ms。因此，转向执行机构闭环控制的延迟累计取值80 ms。

考虑轮胎回正力矩，将辨识的参数(Mr、Br、Keq)、表1中的整车模型参数(Ls)、表2中的线控转向执行机构参数K0以及结合式(30)与式(3)计算得到的ρf代入式(13)，可得含延迟的线控转向系统名义模型的传递函数:

(33)

对试验台架分别实施名义模型含延迟的2DOF IMC、名义模型不含延迟的2DOF IMC以及经典PID控制方法，跟踪斜坡参考输入、正弦参考输入以及变频率参考输入。名义模型含延迟的2DOF IMC中，滤波器阶数取值为m=3、n=3，滤波器参数取值为λr=0.008、λd=0.22。名义模型不含延迟的2DOF IMC中，滤波器阶数取值为m=2、n=2，控制器参数取值为λr=0.01、λd=0.6。PID的增益由MATLAB/Simulink中自动优化增益的模块得到：P=28.6,I=143.2，D=0，其滤波器参数N=100。

由dSPACE PX10控制器发出相同的参考转角输入指令，三种控制方法的试验结果如图9～图11所示。将跟踪过程中的最大跟踪误差与平均跟踪误差进行统计，具体结果如表5和表6所示。可见，与另外两种控制方法相比，对于斜坡、正弦和变频率三种形式的参考输入，名义模型中含延迟的2DOF IMC的最大跟踪误差和平均跟踪误差最小。

(a)跟踪结果

由图10和图11可见，名义模型中含延迟的2DOF IMC不但对固定频率参考输入的跟踪误差较小，而且对变频率参考输入的跟踪误差也保持较小，说明其对频率变化的适应性也较好。

(a)跟踪结果

(a)跟踪结果

值得注意的是，表5和表6中，与其他形式的输入信号相比，在斜坡形式的参考输入下，名义模型中含延迟的2DOF IMC的最大跟踪误差和平均跟踪误差比其他两种控制方法减小的比例最大。这是由于斜坡输入信号从0 rad突然以一个较大的斜率增大，而且在2 s时斜率突变为0，考验系统从静止迅速开始转动的动态响应能力。由于名义模型中含延迟的2DOF IMC比其他两种控制器的动态响应更敏捷，因此，以斜坡信号作为参考输入，名义模型中含延迟的2DOF IMC的优势更加明显。

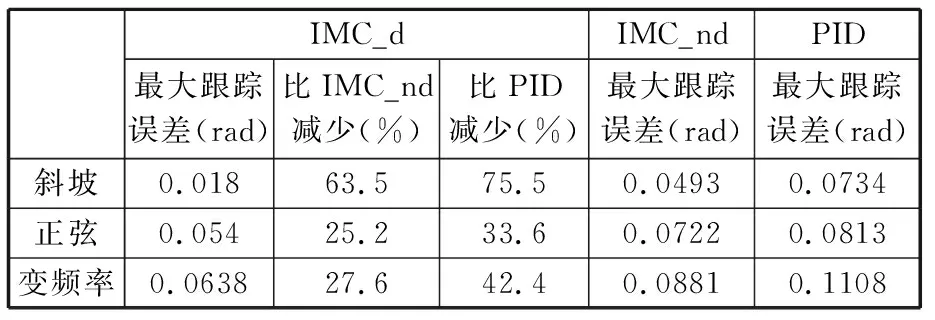
表5 三种控制方法的最大跟踪误差

表6 三种控制方法的平均跟踪误差

5 结论

本文考虑线控转向机构中延迟的影响，建立延迟环节模型，设计二自由度内模控制系统，推导跟踪控制器和抗干扰控制器并给出了二自由度内模控制下线控转向系统的闭环稳定条件。通过MATLAB/Simulink仿真给出不同延迟作用下的转角跟踪性能，与名义模型不含延迟环节的内模控制以及经典PID控制相比较，揭示三种方法的跟踪性能随延迟量变化的规律，表明当延迟较大时采用含延迟的名义模型可显著提高二自由度内模控制的转角跟踪性能。更进一步，在二自由度内模控制框架下，比较采用全极点近似、Taylor近似和Padé近似三种延迟近似方法的控制器跟踪误差随延迟量变化的规律，表明全极点近似方法受延迟量的影响最小。经线控转向台架试验验证，采用全极点近似方法的二自由度内模控制跟踪精度较高，对延迟的适应性较好。