铝合金铸造工艺的Metropolis准则蜂群算法优化

张井柱，翁月宏

（长春科技学院汽车与机械工程分院，吉林 长春 130600）

1 引言

传统的铸造工艺设计主要依赖工程师个人经验，但是当铸件较为复杂时，需要经历一个“生产-检测-调整工艺-再生产-再检测”的循环过程，使得铸件研发周期长、研发成本高[1]。因此，研究铸造工艺的智能优化方法，对于缩短研发周期、降低研发成本意义重大。

以低压铸造工艺优化为研究内容，国内外对低压铸造工艺的研究主要集中在以下方面：（1）铸件的微观组织分析[2]；（2）不同工艺参数对铸件性能的影响。对低压锻造工艺的研究方法包括解析法、实验法、数值模拟法等。文献[3]研究了在低压铸造中加压速度对模具填充的影响，使用流体体积法建立了双相流动模型，描述了铸造模具的填充行为。文献[4]在对工业零件的低压铸造过程中，施加不同的压力幅值，结果表明压力幅值大时会产生较大的液体流速。文献[5]研究了短碳纤维含量和碳纤维长度对铝基复合材料铸件应力、应变分布的影响规律。文献[6]分析了浇注温度和熔炼温度对铸件力学性能和磨损性能的影响，在此基础上进行了参数优化。当前对于铸造工艺参数的优化研究缺陷是，基于拟合模型或影响进行人为优化，是一种有限次试验和比较的优化，优化结果未必为最优的工艺参数，为了实现全域优化，提出智能优化方法。针对铝合金铸造工艺的优化问题，使用单隐藏层神经网络拟合工艺参数与质量参数间的非线性关系。以提高铸造效率和铸件质量为目标，建立了优化模型。提出了Metropolis准则蜂群算法的模型求解方法，经过工艺参数优化，达到了提高铸件质量和生产效率的目的。

2 实验设计

2.1 铸件结构简介

以航空发动机的铝合金壳体零部件铸件为研究对象，此铝合金铸件为小型薄壁件，三维尺寸为（225×192×90）mm，铸件质量为1.69kg，最小壁厚为5mm，其三维仿真模型，如图1所示。此铸件底部为圆形法兰面，底部与顶部由4个通道连接，铸件顶部为圆环形凹槽，凹槽内有圆孔。

图1 铸件三维模型Fig.1 3-Dimension Model of Casting

铸件材料选用ZL101H铝合金，合金材料，如表1所示。

表1 罐体材料成分Tab.1 Tank Material Composition

2.2 铝合金低压铸造原理

低压铸造原理，如图2所示。在封闭保温装置中将合金进行熔炼并保温，在保温装置中充入干燥气体并逐渐增大气体压力，在气体压力作用下，合金液沿升液管上升至浇注口处，此过程对应图2（b）中的t1过程，升压速度为v1=P1∕t1；继续增大气体压力，使合金液逐渐填满整个模具，充型过程结束，此过程对应图2（b）中的t2过程，升压速度为v2=（P2-P1）∕t2；充型结束后继续缓慢增压，使铸件表面形成硬壳，此过程对应图2（b）中的t3过程，升压速度为v3=（P3-P2）∕t3；而后继续保压直至浇注口处完全凝固，此过程对应图2（b）中的C D段；铸件凝固完毕后泄压，使合金液回流至保温装置中，此过程对应图2（b）中的D E段，自此低压铸造完毕，铸件进行后续处理[7]。

图2 低压铸造原理Fig.2 Low Pressure Casting Principle

使用的封闭保温装置为GR-750坩埚电阻炉，模具为SPrint砂型打印设备打印的3D整体砂芯，如图3所示。

图3 打印砂芯Fig.3 Printed Sand Core

2.3 优化问题描述与建模

（1）确定优化目标。以凝固时间最短、缩松面积最小为优化目标。凝固时间不仅决定了铸件的生产效率和生产周期，同时铸件晶粒大小、显微组织分布等影响铸件性能的参数也与凝固时间有关。缩松是低压铸造最主要和最常见的内部缺陷，铸件的缩松处会发生应力集中现象，严重影响铸件的力学性能。综上所述，选择凝固时间最短和缩松面积最小为优化目标，目标函数为：

式中：G—目标函数；S sh—缩松面积；S sh_se t—设定的缩松面积目标值，取S sh_s et=1500；t so—凝固时间；t s o_set—设定的凝固时间目标值，取t so_set=250；设置S sh_set、t s o_set等参数的目的是将不同优化目标调整至同一数量级。w1、w2—缩松面积和凝固时间的优化权值，取w1=w2=0.5。

（2）选择优化参数。在低压铸造工艺参数中，合金液的浇注温度t ca、充型速度v mo和保压压力p pr等对铸件的凝固结晶和力学性能有重要影响。合金液浇注温度直接影响铸件的凝固时间，进而影响铸件的晶粒组织。充型速度影响了合金液与模具间的换热，当充型速度大时，合金液与型腔的换热就会减少，热量损失减少，但是过大的充型速度会造成合金液紊流，甚至冲散砂芯。保压压力对铸件的冷却过程产生影响，在保压阶段合金液与模具间热量传递较快，则铸件表面首先凝固结壳，保压压力影响铸件的结壳和补缩。综合以上分析，选择浇注温度、充型速度和保压压力进行优化，参数的优化范围为：浇注温度（685～730）℃、充型速度（35～75）mm∕s和保压压力（20～45）kPa。

3 实验设计与数值神经网络拟合

首先进行实验设计，依据Anycasting软件使用有限元法对铸造过程进行模拟，得到不同实验条件下的凝固时间和缩松面积，而后使用神经网络拟合质量参数和工艺参数间的非线性关系。由于篇幅有限，这里不再给出铸造过程的数值模拟分析。

3.1 实验设计及数据预处理

按照2.3节给定的参数变化范围，浇注温度从685℃到730℃每5℃取一个值，共取11个参数值；充型速度从35mm∕s到75mm∕s每10mm∕s取一个值，共取5个值；保压压力从20kPa到40kPa，每10kPa取一个值，共取3个值。由此共设计165组实验，使用Any⁃casting软件拟合铸造过程，得到实验值。由于数据量较大，在此仅给出5组原始实验数据，如表2所示。

表2 原始实验数据Tab.2 Original Experiment Data

使用神经网络对质量参数与工艺参数间非线性关系进行拟合时，由于输入参数、输出参数之间的量纲不同，数值之间也相差较大，使训练时数值较大的参数占据主导地位，无法充分拟合出输入-输出间的非线性关系。为了解决这一问题，使用归一化处理，消除不同参数间的量级差异。归一化方法为：

式中：x k—原始实验数据；x k′—归一化后数据；x kmax、x kmin—x k的最大值和最小值。

3.2 神经网络拟合原理

使用单隐藏层BP神经网络对铝合金铸造过程的输入-输出关系进行拟合，其网络结构[8]，如图4所示。

图4 神经网络结构Fig.4 Neutral Network Structure

图中所示为n输入m输出的网络结构，隐含层的层数表示隐藏特征的提取深度，一般来讲，隐藏层数越多则输入-输出的拟合精度越高，但是层数的增加也会使计算量极大增加[9]。

对于K+1层神经网络，k=0表示输入层，k=[1，k-1]表示隐藏层，k=K表示输出层，每层神经元数量记为n k。第k-1层向第k层的传递权值记为W k，第k层神经元阈值记为B k，第k层神经元输入值记为Z k，激活值记为A k，则网络的前向传递过程为：

式中：S()—激活函数，常用的激活函数有Sigmoid函数、Tansig函数、Logsig函数等。

基于BP算法的误差反向传播参数训练为：

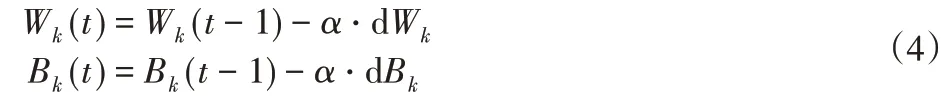
式中：t—训练迭代次数；α—学习率；dW k、dB k—各自的参数梯度。隐含层神经元数量的经验公式为[10]：

式中：n h—隐含层神经元数量；n r—输入层神经元数量；n c—输出层神经元数量；ξ—［1，10］间的整数。

3.3 拟合网络与效果验证

对于2个质量参数与3个工艺参数间的非线性关系拟合，具有2种非线性关系拟合方法。（1）2个输出使用同一个网络结构，构造一个3输入2输出的神经网络；（2）2个输出各自构造一个网络结构，构造2个3输入单输出的神经网络。考虑到神经网络中隐藏层的实质为特征参数提取，而凝固时间与缩松面积的特征差异性较大，因此2个输出各自构造神经网络。

根据式（5）的经验公式及输入输出参数数量，凝固时间拟合网络结构为3-5-1，隐藏层使用激活函数为Tansig函数，输出层使用激活函数为Logsig函数。缩松面积拟合网络结构为3-9-1，隐藏层使用激活函数为Tansig函数，输出层使用激活函数为Log⁃sig函数。前文的165组数据中，145组数据用于训练，20组数据用于测试。以凝固时间为例，对训练过程和测试过程进行说明，缩松面积拟合只给出拟合结果。训练最大次数设置为200，学习率为0.01，训练误差目标为10-4，即当达到训练目标或最大训练次数时，训练过程结束。凝固时间训练过程，如图5所示。

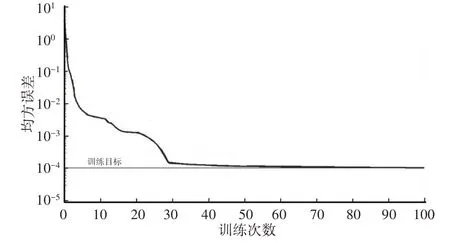
图5 凝固时间训练过程Fig.5 Solidification Time

由图5可以看出，训练迭代至100次时训练误差达到10-4，使用训练完毕的神经网络对测试样本进行预测，结果如图6所示。由图6可以直观看出，神经网络对凝固时间的预测精度较高，预测值与期望值几乎重合。统计20个测试样本的相对误差，凝固时间预测的最大相对误差为0.9%，缩松面积预测的最大相对误差为0.58%。两个数据充分说明了构建的神经网络具有较高的拟合精度，可以对铸件质量进行预测。

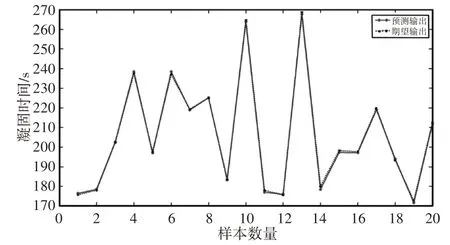
图6 预测结果Fig.6 Predicting Result

4 工艺参数优化模型及求解

在神经网络对铸件质量进行预测的基础上，提出了融合Me⁃tropolis准则的蜂群算法对2.3节建立的优化模型进行求解。

4.1 传统人工蜂群算法原理

人工蜂群算法是受蜂群群体采蜜时分工协作启发而提出的，算法通过以下5个步骤实现：

（1）初始化。记种群数量为NB，初始时种群中所有个体均为侦查蜂，被随机分配到各蜜源位置，即：

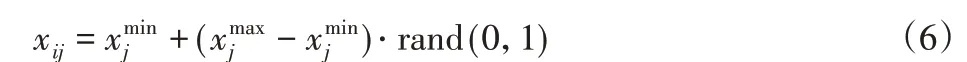
式中，i=1，2，…，NB—蜜蜂个体编号；j=1，2，…，D—解的维度；个位置点的上下界；rand(0，1)—（0，1）间的随机数。

（2）蜜源评价。依据航迹规划的目标函数构造蜜源评价函数，从而对蜜源优劣做出评价。蜜源评价函数为：

式中：fiti—第i只蜜蜂的适应度值。使用蜜源评价函数对蜂群所有个体的蜜源进行评价，蜜源较优的侦查蜂转化为雇佣蜂，蜜源靠后的侦查蜂转化为观察蜂。

（3）雇佣蜂蜜源搜索。雇佣蜂在当前位置附近进行蜜源搜索，当新蜜源适应度优于原蜜源时则选择新蜜源，否则继续进行搜索，雇佣蜂通过这种贪婪规则不断优化蜜源，雇佣蜂的位置更新方法为：

（4）观察蜂选择与邻域搜索。雇佣蜂通过摇摆舞将自身蜜源信息传递给观察蜂，观察蜂依据适应度值计算选择各蜜源的概率，为：

式中：pi—观察蜂选择第i只雇佣蜂的概率；NB′—雇佣蜂数量。

由式（9）可知，依据各蜜源适应度值确定选择概率，可以保证较优蜜源更大的选择概率，确保更优蜜源附近的细致搜索。观察蜂选择雇佣蜂后与雇佣蜂一起进行邻域搜索，观察蜂的位置更新方法和蜜源选择方法与雇佣蜂一致。

（5）侦查蜂的蜜源搜索。若某只蜜蜂在一个蜜源邻域连续搜索次数达到一个上限且适应度值没有明显提高，则此蜜蜂放弃当前蜜源，转化为侦查蜂。侦查蜂的位置更新方式与式（6）一致。

4.2 融合Metropolis准则的蜂群算法

（1）改进观察蜂对雇佣蜂的选择概率。在传统算法中，观察蜂依据雇佣蜂蜜源适应度值确定跟随概率，这种方法利于算法收敛，但是却容易陷入局部最优。作者认为连续被优化的蜜源附近更具有搜索潜力，更具有搜索价值，基于这一考虑，设置变量D1(i)、D2(i)用于记录蜜源连续更新次数。当蜜源i更新时，令D1(i)=0，D2(i)=D2(i)+1；当蜜源i保持不变时，令D2(i)=0，D1(i)=D1(i)+1。D1(i)、D2(i)最大值均设定为Limit，Limit表示局部搜索最大次数。

经过多次搜索未更新的蜜源，说明其邻域搜索意义不大，已经陷入了局部最优。而多次更新的蜜源邻域搜索活力较大，对算法寻优指导意义更大，因此应将观察蜂更大概率地分配到此区域。记G(i)为蜜源i的评估分值，每个蜜源基础分为50，各蜜源得分计算方法为：

式中：G(j)—第j个雇佣蜂蜜源的得分，NB′—雇佣蜂数量。分析式（10）和式（11）可知，观察蜂选择雇佣蜂时既考虑了适应度，同时考虑了连续优化次数，观察蜂既选择优质蜜源，同时选择有潜力蜜源。

（2）改进蜜源评价方法。传统算法中，依据蜜源适应度值大小决定是否接受蜜源，这种选择方式过早地将有潜力的蜜源淘汰掉，使算法前期收敛较快，算法后期收敛较慢。为了解决这一问题，提出了蜜源选择的Metropolis准则[11]，蜜蜂由当前蜜源转向新蜜源的转移概率为：

式中：p(o→n)—由当前蜜源o向新蜜源n转移的概率，下降函数T(t)=T(t-1)⋅σ，σ—退火系数，取σ=0.8。

分析式（12）可知，当新蜜源适应度小于原蜜源时，仍有一定的转移概率，有利于保留具有潜力的蜜源；在算法初期，退火温度T(t)较高，适应度差的蜜源转移概率较大，保留有潜力蜜源的概率也大，有利于算法跳出局部最优；算法后期退火温度逐渐减小，算法更加“关注”优质蜜源，更多蜜蜂在优质蜜源邻域内细致搜索，提高寻优精度。

4.3 改进人工蜂群算法流程

根据优化参数和优化目标，将蜜源位置维度设置为3维，即X=[tca，vmo，ppr]，采用十进制编码方式。算法的搜索空间在前文中已明确。根据上节对人工蜂群算法机理的改进，基于改进人工蜂群算法寻优的步骤为：

（1）初始化算法参数：种群规模N B、局部搜索最大次数Limit、最大迭代次数MaxCycle，设置trial(i)=0，iter=0；

（2）进行种群初始化，依据适应度值将蜜蜂分为雇佣蜂和观察蜂；

（3）雇佣蜂进行邻域搜索，依据Metropolis准则判断是否接受新蜜源，使用摇摆舞将蜜源信息传递给观察蜂；

（4）观察蜂根据动态选择概率选择雇佣蜂，而后与雇佣蜂一起进行邻域搜索，依据Metropolis准则判断是否接受新蜜源，若蜜源更新则trial(i)=0，若不更新则trial(i)=trial(i)+1；

（5）判断trial(i)>Limit是否成立，若成立则第i只蜜蜂转化为侦查蜂进行随机搜索，若不成立则转至下一步；

（6）输出全局最优蜜源，iter=iter+1，判断iter>MaxCycle是否成立，若成立则算法结束，否则转至（3）。

5 实验验证及分析

5.1 参数优化过程

为了验证Metropolis准则蜂群算法在铸造工艺优化中的性能，同时使用传统蜂群算法和Metropolis准则蜂群算法进行参数优化。为了保证公平，两个算法相同的参数设置为同一值，不同的参数按照算法自身性能最佳设置。共同参数设置为：算法最大迭代次数MaxCycle=250，种群规模N B=60，局部搜索最大次数Limit=10。目标函数随两种算法的迭代过程，如图7所示。

图7 优化迭代过程Fig.7 Optimizing Iteration Process

从图中可以看出，传统蜂群算法迭代至110次时目标函数值不再变大，Metropolis准则蜂群算法迭代至46次时目标函数值不再变大，说明Metropolis准则蜂群算法的收敛速度快于传统蜂群算法，优化耗时短于传统蜂群算法。从优化深度看，Metropolis准则蜂群算法的优化程度深于传统蜂群算法，即Metropolis准则蜂群算法搜索的结果优于传统蜂群算法。这是因为Metropolis准则蜂群算法中使用观察蜂的动态选择策略和Metropolis准则的蜜源评价策略，既能够有效选择较优蜜源，也能够保留具有潜力的蜜源。

传统蜂群算法搜索的最优工艺参数为：浇注温度t ca=725.6°C、充型速度v mo=42.26mm∕s、保压压力p p r=30.35kPa；此工艺参数对应的神经网络拟合值为：凝固时间t so=241s、缩松面积S sh=1526.7mm2。Metropolis准则蜂群算法搜索的最优工艺参数为：浇注温度t ca=714.2°C、充型速度v mo=35.04mm∕s、保压压力p pr=33.83kPa；此工艺参数对应的神经网络拟合值为：凝固时间t so=233s、缩松面积S sh=1157.8mm2。

5.2 仿真验证

根据5.1节的工艺参数，使用Anycasting软件根据有限元法对铸造过程进行模拟，得到仿真铸件缩松缺陷的概率分布，如图8所示。图中颜色越鲜艳表示缩松缺陷的概率越大。

图8 仿真铸件的缩松缺陷分布Fig.8 Shrinkage Distribution of Simulation Casting

由图8可以直观看出，两种算法优化后的铸件缩松主要分布在底部圆环和底部内环。由于底部内环和底部圆环间通过薄壁连接，因此铸造时合金液的流动阻力较大，使得底部内环补缩时阻力较大，缩松缺陷概率增大。比较两种方法优化的仿真铸件，Metropolis准则蜂群算法优化的铸件缩松概率及面积明显小于传统蜂群算法的优化结果，证明了Metropolis准则蜂群算法在铸造工艺优化中的有效性。

5.3 实际生产验证

将优化工艺参数应用于实际铸造过程，验证参数在实际生产中的性能。为了将优化的工艺参数应用于实际生产中，将参数微调为整数，即：浇注温度t ca=715°C、充型速度v mo=35mm∕s、保压压力p p r=34kPa。将ZL101H铝合金在GR-750坩埚电阻炉中熔化，并保温在715℃，以低压铸造的方式将其注入到图3所示的砂芯模具中，铸件冷却后进行清砂得到铸件。为了观测铸件的微观组织并进行硬度检测，将铸件沿顶部中心线剖开，得到剖面图，如图9所示。图中A、B、C三点为试验采样点。

图9 铸件剖面Fig.9 Section of Casting

从图9的A、B、C三点处取试验试样，进行打磨抛光后使用腐蚀液进行腐蚀，在MM-4C型金相显微镜下观测晶粒组织，结果如图10所示。

图10 显微组织Fig.10 Micro-Structure

由图10可以直观看出，铸件的显微组织均匀，无明显缩松缺陷。另外，位置A处于位置B处的凝固时间接近，因此两处的显微组织极为相似。使用HRS-150型洛氏硬度计测量三处铸件试样的硬度，A处硬度为51.3HRB，B处硬度为53.5HRB，C处硬度为52.8HRB，三个位置均满足大于45HRB的硬度要求，可以应用于实际生产过程。

6 结论

研究了铝合金铸造工艺的优化问题，使用神经网络拟合了工艺参数与质量参数间的非线性关系，使用Metropolis准则蜂群算法进行了参数优化，经验证得出以下结论：

（1）神经网络对铸造工艺参数与质量参数间的非线性关系具有较高的拟合精度；

（2）Metropolis准则蜂群算法的优化深度和优化精度高于传统蜂群算法；

（3）经优化，铸件的凝固时间和缩松面积减小，提高了铸造效率和铸件质量。