基于集中质量法发动机曲轴系统扭振特性分析

刘义付，孙瑞霞

（黄河交通学院，河南 焦作 454000）

1 引言

汽车的曲轴是发动机中最主要的运动部件之一，其轴系为弹性力学系统，在发动机工作过程中，因为曲轴系统承受着由活塞连杆传来的复杂变化的高压气体冲击作用力和活塞连杆自身往复运动过程产生的惯性力[1]，从而带来周期性变化的载荷，再加上曲轴前后要输出转矩，使曲轴轴体产生交变的弯曲、扭转和拉伸的应力，产生与转速相关的扭转振动频率和振幅，造成曲轴轴系工作过程中的扭转共振，引起各种失效，对曲轴自身强度带来考验。因此，有必要采用不同的方法对轴系的扭转振动特性进行分析，以设计合理的减振方式。

国内外学者对此进行了一定的研究：文献[2]采用系统当量法对轴系的固有振动特性进行分析；文献[3]基于有限单元法对轴系各部分单独建模获得整体的刚度特性；文献[4]采用非接触式测试方法，对某款发动机曲轴轴系的扭转振动特性进行测试；文献[5]采用仿真与试验相结合的方法，对某曲轴轴系的共振频率进行测试，对扭转减震器进行设计。

针对某四缸发动机扭转振动特性进行分析，采用集中质量法对曲轴轴系进行扭转振动建模，获取系统的特征方程，分别应用并对比了二自由度和六自由度当量系统方法，获取轴系的自振频率和振型，并获取低谐次的共振转速；采用非接触式试验测试，对比曲轴系统试验数据和理论分析数据，获得校准后的发动机轴系扭振计算模型，对比了两种求解模型结果的差异性，并对理论计算结果进行修正。

2 曲轴轴系扭转振动分析

2.1 扭振模型

相邻两圆盘之间以弹性轴段连接，其刚度就是被连接两圆盘间实际轴段的刚度或柔度[6]。所要分析的发动机曲轴系统三维实体模型图，如图1（a）所示；该发动机曲轴系统的连杆图型，如图1（b）所示；该发动机曲轴扭转振动分析力学模型，如图1（c）所示。

图1 发动机曲轴轴系模型Fig.1 Engine Crankshaft Model

图中：In—各个集中质量的转动惯量；Cn—各个集中质量的外阻尼；hn—系统中第（n-1，n）轴段的内阻尼；kn—系统中第（n-1，n）轴段的刚度；Tn—各个集中质量的干扰力矩。可得出此当量系统的扭转振动的运动方程组为：

2.2 模型参数分析

2.2.1 转动惯量

发动机曲轴系统的转动惯量计算中，主要涉及三部分：曲轴、飞轮等旋转件的转动惯量，活塞连杆等往复运动部件的转动惯量和由曲轴正时齿轮驱动的凸轮轴齿轮等零件的转动惯量[7]。对于发动机曲轴当量系统的转动惯量，把曲轴系统分为六个当量刚性体求取转动惯量：由曲轴前端质量块转动惯量与皮带轮转动惯量整合成曲轴前端当量转动惯量；分别由1至4缸的曲拐转动惯量与各缸活塞连杆机构的转动惯量整合成1至4缸曲拐当量转动惯量；由曲轴后端质量块转动惯量与飞轮转动惯量整合成曲轴后端当量转动惯量[8]，如图2所示。

图2 曲轴旋转件转动惯量的质量块Fig.2 Mass of Moment of Inertia of Crankshaft Rotating Parts

六个总当量转动惯量值，如表1所示。

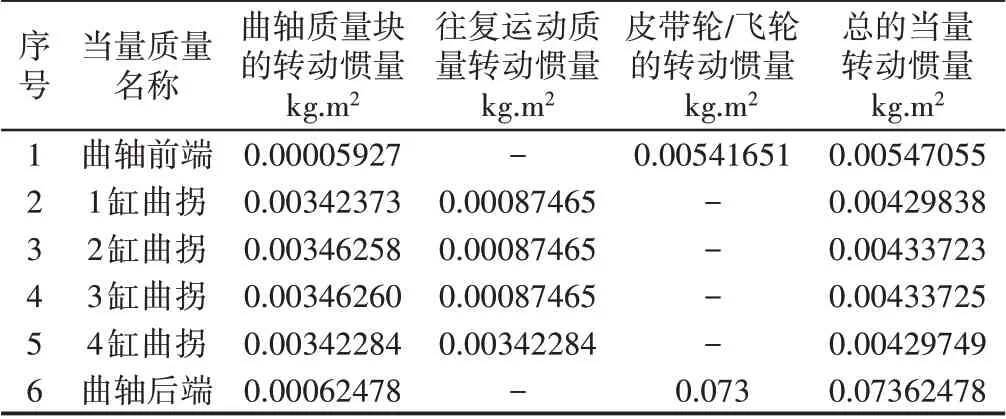
表1 当量模型转动惯量Tab.1 Equivalent Model Moment of Inertia

2.2.2 刚度分析

轴段的刚度是轴段被扭转单位角度（1rad）所需的扭矩，用符号K表示。根据材料力学，若在长度为L的轴段两端加一对扭矩M时，轴段两端相对扭转角度为Δφ，则轴段的扭转刚度为：

式中：G—轴段材料的剪切弹性模量；

J P—轴段截面的极惯性矩；

M—施加力矩；

Δφ—相对扭转角度；

K—轴段的扭转刚度。

这样由上述公式就可计算出每段轴段的扭转刚度K值。所研究的发动机曲轴扭转振动模型轴段刚度计算结果，如表2所示。

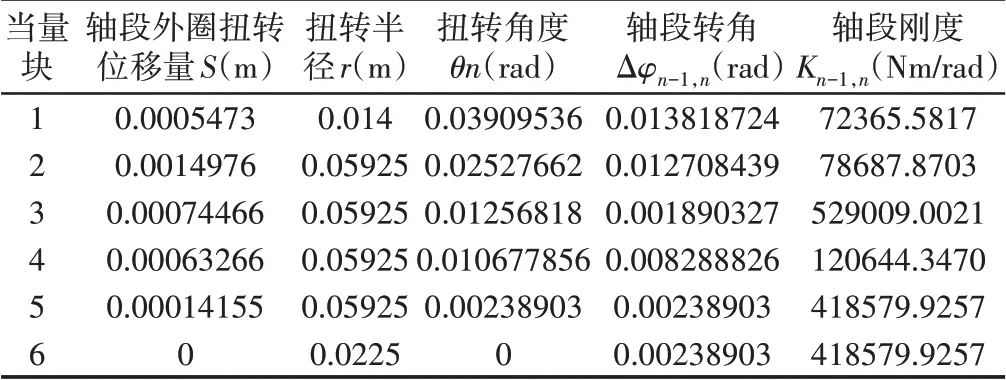
表2 刚度计算结果（施加力矩1000Nm）Tab.2 Stiffness Calculation Results（Applying Torque 1000Nm）

3 扭振模型特性分析

3.1 简化为六自由度自由扭转振动特性分析

计算曲轴当量系统自由扭转振动时，干扰力矩［T］=0；而且发动机曲轴系统是弱阻尼系统，在计算自由振动时可不用考虑阻尼的影响，按无阻尼自由振动进行计算，即扭振方程中阻尼矩阵为［C］=｛0｝，对于该方程组，其有解的条件是［K-p2I］的各个元素组成的行列式为0，这样就归结为求特征值p2和特征向量｛a｝的问题[9]。用MATLAB计算软件编程计算求解后，得到的发动机曲轴系统自由扭转振动计算结果，如表3所示。根据计算结果得出的相对振幅，绘制出1至3结点的振型，如图3所示。

表3 六自由度自由扭转振动结果Tab.3 Six Degrees of Freedom Free Torsional Vibration Results

图3 自由扭振振型Fig.3 Free Torsional Vibration Mode

对于结点数为0，自振频率也为0的情况，是各个当量质量的相对振幅相等，即aj（1）=a1=1。这种状态是整个曲轴系统的整体旋转，而不是扭转振动。该六自由度当量系统的自由振动实际上是2阶到6阶的共5个主振动的叠加。

3.2 简化为两自由度的自由扭转振动特性分析

对轴系进行两自由度的简化计算，过程如下：

（1）对于转动惯量I：将曲轴前端及1至4缸曲柄当量系统转动惯量合成一个等效的转动惯量I1′，放置于3缸曲柄位置，其值为简化前各个当量转动惯量之和；曲轴后端当量系统保持不变[10]，设置为I2′，即：

（2）对于轴段刚度K：I1′和I2′之间的轴段刚度，设置为K′，按3缸曲柄之后的各个当量系统间的刚度串联计算而成，即：

（3）特征根为：

（4）系统固有频率为：

（5）相对振幅比为：

这样求出二自由度自由扭振模型转动惯量0.0227409kg.m2、0.07362478kg.m2，轴段刚度79565.9961Nm∕rad；f=311Hz。相应的二自由度轴系自由扭转振动计算结果，如表4所示。

表4 两自由度自由扭转振动结果Tab.4 Two Degrees of Freedom Free Torsional Vibration Results

3.3 两种模型特性比较分析

在两自由度盘轴系统中，计算得到的轴系固有频率与六自由度盘轴系统中的轴系一阶固有频率相差较大；对比两者单结点振型图可以发现，在线形上是比较类似的；两个振型图中的结点位置处均出现在曲轴的后端，即3缸曲拐质量块与曲轴后端质量块之间；但在曲轴后端质量块的相对振幅上有一定的偏差。从六自由度扭振系统单节点振型图上可以看出，轴系各个当量质量块的扭转角位移相差不大，斜率最大处出现在4、5当量质量块间；在六自由度的双结点振型图中，可以发现轴系的曲轴前端、1、2曲拐当量质量的角位移与3、4曲拐、曲轴后端当量质量的角位移反向。两自由度简化系统与六自由度简化系统的较大相异特点，说明在简化过程中，还有一些变量是不够准确的，这需要由试验测得的数据来校核。

3.4 曲轴系统共振转速

所研究发动机，在自由振动状态下求得轴系扭转振动的自振频率后，即可求出发动机的临界转速范围，如图4所示。

图4 发动机单结点共振转速分布Fig.4 Engine Single Node Resonance Speed Distribution

由图可知，当激振简谐次数低于12次时，对于该发动机轴系的主谐次和次主谐次，在工作转速范围内仅对单结振动存在的共振转速，如表5所示。

表5 主、次谐次对应共振转速Tab.5 Primary and Secondary Harmonics Correspond to Resonance Speed

4 试验测试分析

由于引起二阶共振的激振力矩谐波的简谐次数比引起高阶共振的简谐次数低得多，二阶主刚度Kp2比其他高阶刚度小得多，所以轴系的第一个强共振应该是次数最低的一两个主谐波或次主谐波引起的二阶共振。采用非接触式扭转振动测试方法，试验原理，如图5（a）所示。试验台，如图5（b）所示。

图5 扭振测量装置示意图Fig.5 Diagram of Torsional Vibration Test

由发动机曲轴扭振测试得到的发动机曲轴无前端皮带轮质量、无活塞连杆质量的测试数据，如图6所示。应用前面章节计算自由扭振频率的方法，对所分析的发动机轴系在无前端皮带轮质量、无活塞连杆质量的情况下，进行分析计算，得到的自振频率值，如表6所示。

图6 扭转测试试验数据Fig.6 Torsion Test Data

表6 自振频率值Tab.6 Natural Vibration Frequency Value

测试数据中的最大振幅应该为二阶固有频率处的共振幅值，保持各个质量块处的转动惯量不变，对轴段的刚度进行调整，使得曲轴前端和1缸曲拐间轴段刚度不变，各缸曲拐间轴段刚度保持一致，4缸和曲轴后端的轴段刚度不变，经过反复试算，得到校准后使原计算的二阶频率f2=452Hz调整为f2*=486Hz的轴段刚度值，如表7所示。

表7 试验修正后各轴段刚度Tab.7 Stiffness of Each Shaft Segment

根据表7的结果，对模型参数进行修正，计算得出了曲轴轴系转化为六自由度当量系统的自由振动计算结果，如表8所示。振型图，如图7所示。以上参数值是可以应用到接下来扭振减振器设计中去的。应用校准后的参数值计算曲轴两自由度当量系统的自由振动频率值，如表9所示。

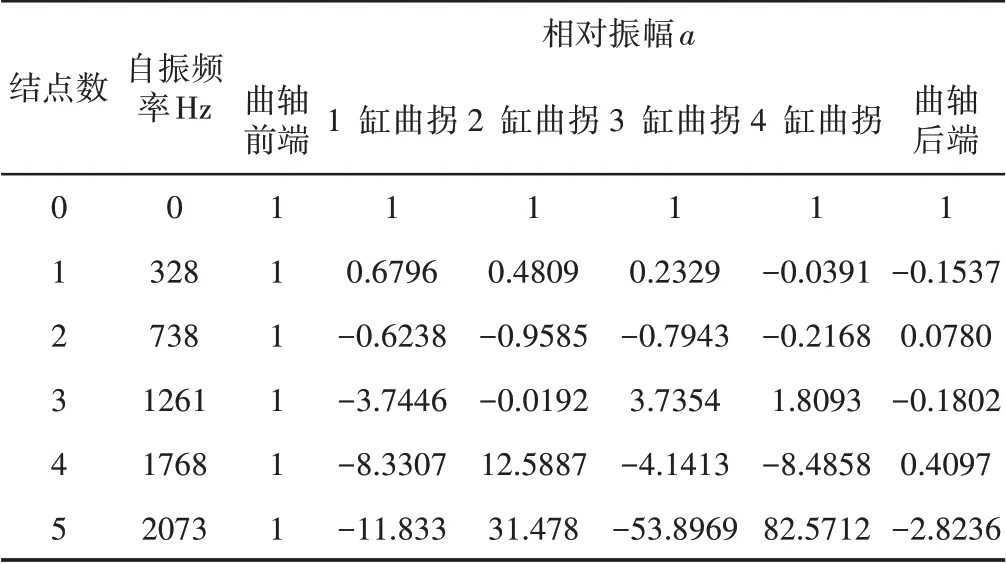
表8 六自由度计算结果Tab.8 Six Degrees of Freedom Calculation Results

图7 六自由度振型Fig.7 Six Degrees of Freedom Vibration Mode

表9 两自由度计算结果Tab.9 Two Degrees of Freedom Calculation Results

通过对比校准后的六自由度盘轴系统与两自由度盘轴系统的固有频率，可以看到自振频率值已经非常接近，仅相差0.003%左右。这种接近度，也说明了校准后的模型参数，虽然还有一定的误差，由于系统中的弱阻尼没有考虑进去的原因，但已经可以应用于实际设计中。

5 结论

（1）二自由度和六自由度当量系统法均可对曲轴轴系的自由振动特性进行分析，二者的误差在4%以内；

（2）在发动机的转速范围内，对于该发动机轴系的主谐次和次主谐次，存在对个共振转速，需要设计专门的扭转减振器进行控制；

（3）基于扭转振动实验测试，对曲轴轴系的扭转振动模型进行修正，可以显著提高二自由度和六自由度当量系统法获得的轴系自由振动特性的准确性，二者的误差控制在较低水平；同时模型分析与试验测试结果基本一致，表明分析模型的可靠性，为实际设计提供重要参考。