单神经元与IPSO的双电机同步控制研究

庞雨花，吴 杰，王 华

（1.常州机电职业技术学院，江苏 常州 213164；2.南京工业大学机械与动力工程学院，江苏 南京 210000）

1 引言

在工业自动化生产领域，单电机的驱动方式在大负载、长距离和多变量控制等场合，已越来越难以满足现代工业技术发展的需求，所以要求双电机同时工作的场合日益增多[1]。当前针对双电机同步控制的研究主要在控制结构和控制方法的改进这两个方向[2]。传统PID控制方法原理简单、易于应用，被广泛用于电机调速系统中，但仅靠PID难以进行高精度控制。为此，国内外学者将遗传[3]、蚁群[4]、模糊控制、粒子群优化（PSO）[5]等算法应用到电机控制中，取得了优秀的效果。其中，PSO算法避开了蚁群算法计算量大、模糊控制对经验要求高、遗传算法复杂易早熟的缺点，引起了国内外学者的广泛关注[6]。而双电机同步控制结构有主从、并行和交叉耦合，其中交叉耦合可以反映任何一台电机的负载变化，可显著增强系统的同步性能[7]。综上所述，以两电机同步控制系统为研究对象，针对其在启动和有负载扰动时会产生较大的转速同步误差的问题，从控制结构和控制方法两方向进行改进。在控制方法上设计了IITAE指标下的改进粒子群优化速度环控制器，来提高系统启动稳定性和抗扰动性能。在控制结构上采用单神经元作为交叉耦合控制器，进一步增强系统的同步性和抗扰动性能。最终进行仿真与实验验证了该控制策略的有效性与可行性。

2 双永磁电机同步控制系统结构设计

以双永磁同步电机（PMSM）为对象，其整体结构，如图1所示。

图1 双永磁电机同步控制系统结构Fig1 Structure of Synchronous Control System for Dual-PMSM

图中：ω—电机给定参考转速；KP、K I—速度环PI控制器的参数；Ti1、Ti2—负载转矩；ω1、ω2—两电机的实际转速；iq—IPSO-PI控制器的输出；id固定—0；θ—转子角位置。

从图1可以发现，与一般双PI并行同步控制系统相比，所设计的双PMSM同步控制系统采用IPSO-IITAE来增强单电机的控制精度，为提高双电机同步性能打下基础。接着采用单神经元耦合器将两电机的转速同步差处理后反馈到两电机的转速环，进一步提高双PMSM系统的同步性能。

2.1 改进粒子群优化速度控制器设计

传统的粒子群优化控制在一定程度上可以得到较好的PI控制参数，从而取得相对较好的控制效果[8]。但由于传统PSO有易陷入局部最优解和收敛速度在迭代后期显著降低等缺点，为了提高最优PI参数搜索的速度和准确性，实现两电机的高精度控制，双PMSM均使用参数与结构相同的IPSO-IITAE控制器。其设计方法如下。

2.1.1 动态非线性惯性权重设计

为了确保双PMSM的高同步性能，就需要先优化单个电机的控制效果。而传统PSO并不能保证优秀PI参数的产生，所以我们针对惯性权重进行改进。

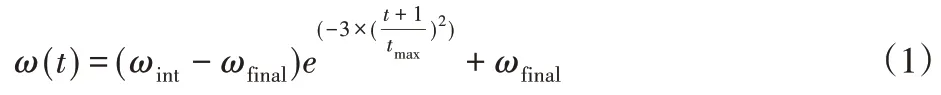
式中：ω（t）—惯性权重；ωint—初始权重（一般取0.9）；ωfinal—最大迭代时的权重（一般取0.4）；t—当前迭代次数；tmax—最大迭代次数。

其随迭代次数改变的曲线，如图2所示。从图2可以看出变化曲线为前凸后凹的递减函数。由于ω的值设置过大会提高系统的全局寻优性能，降低局部寻优性能，反之亦然。所以设计的动态非线性惯性权重的曲线前凸后凹，保证在迭代初期一直保持着较大的权重，使PSO迭代前期保持注重全局寻优的状态，后期保持较小的权重，侧重局部寻优。以此避免算法陷入局部最优，加快收敛速度，提高算法性能。

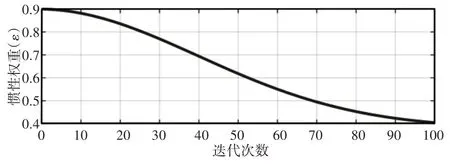
图2 惯性权重随迭代次数变化的曲线Fig.2 Curve of Inertia Weight Varying with Iteration Times

2.1.2 性能评价函数设计

为了将IPSO应用于速度环PI控制器参数寻优中，必须使用性能评价函数来评估粒子性能。工程实际中常采用的是时间与绝对误差乘积的积分（ITAE）。

但ITAE只是量化了系统响应过程中的过渡时间与过渡误差，没有区分系统动态过程中的超调误差。所以采用ITAE的系统在响应前期有较大超调量，不能稳定上升达到设定转速，影响电机启动时的同步性能。为此设计了改进的时间与绝对误差乘积的积分（IITAE）。

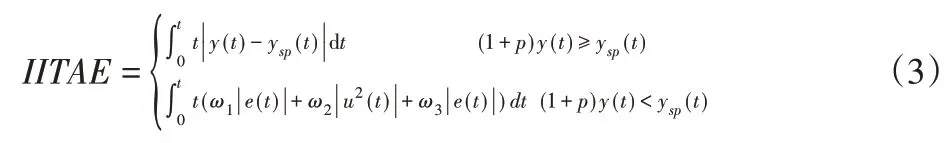
式中：p—超调控制精度；u（t）—控制器输出；y（t）—转速设定值；ysp（t）—实际转速值；e（t）—系统误差；ω1、ω2、ω3—权值，且ω3≫ω1。

通过p的引入来限制过大的超调量，使得IITAE能够保证速度环稳定，准确且无较大超调地跟踪指令。

2.2 单神经元速度耦合器设计

传统双电机交叉耦合同步控制以同一比例值作为速度耦合控制器直接补偿两电机的转速误差，但是这一比例值需要人工经验调节，同步性不高。而人工神经网络不仅对这种非线性系统能够任意逼近，而且可以对几乎所有不确定性和非线性系统实现控制[9]。但是常规神经网络修正时间和权值训练长且组成结构复杂，而单神经元与神经网络类似，可以任意逼近非线性函数，结构相对简单，可靠性高，易于在控制系统中实现，可以进行实时控制[10]。单神经元耦合器结构，如图3所示。

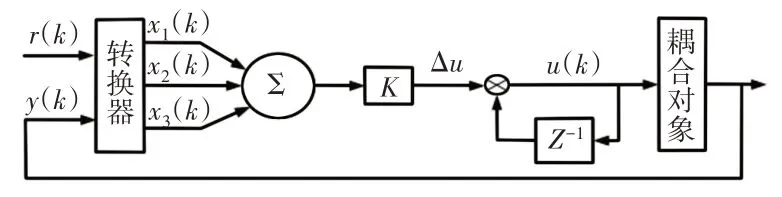
图3 单神经元耦合器结构Fig.3 Structure of Single Neuron Coupler

采用有监督Hebb学习算法对单神经元的输入、输出以及输出的偏差与权值之间相互联系，其算法公式是：

式中：η1、η2、η3—学习速率；wi（k）—权值；xi（k）—状态输入信号；u（k）—输出；Δe（k）—控制偏差增量；e（k）—反馈值与设定值的偏差。

通过单神经元算法对权值的持续调整，提高了单神经元速度耦合器的自适应和自学习能力，可以提高同步控制精度，降低同步误差。

3 系统仿真与分析

3.1 系统搭建与参数设置

根据之前所设计的双电机控制结构在Matlab∕Simulink下建立双PMSM同步控制系统的仿真模型，主要包括：IPSO-IITAE控制器，单神经元耦合器，PMSM矢量控制等。双PMSM同步控制系统仿真时电机均空载启动，目标转速1000r∕min，稳定后施加15N·m的负载扰动。仿真中各个控制器与两电机的参数，如表1所示。

表1 算法控制器与永磁同步电机参数Tab.1 Algorithmic Controller and PMSM Parameters

3.2 PI参数优化结果分析

在粒子群算法优化PI参数中，为了展示IPSO的优化能力，在IITAE指标下对电机分别使用传统PSO与IPSO进行比较，两者的适应度变化过程，如图4所示。

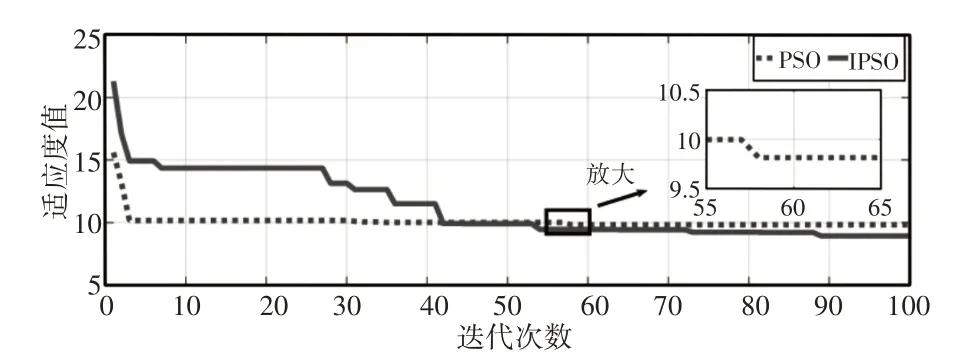
图4 适应度值变化过程Fig.4 Fitness Value Change Process

由图4可以得知，在相同的适应度指标下，虽然两算法都使电机的适应度逐渐减小，但是传统PSO优化57次达到收敛，而IP⁃SO在第53次迭代后适应度值就小于传统PSO，显示出了IPSO更好的收敛效率。从整体上看，PSO在第4次迭代后，适应度值就不再有较大的变化，陷入了局部最优，而IPSO因为动态非线性惯性权重曲线先凸后凹的设计，使得其在53次迭代前均处于全局寻优的状态，避免了困于局部最优解的情况，且在53次到88次迭代中侧重局部寻优，得到了比PSO更为优秀的PI参数。

3.3 结果分析

为了进一步体现IPSO的优化控制效果并展示所设计的II⁃TAE性能评价函数的评价性能，针对IPSO-IITAE、IPSO-ITAE以及PSO-ITAE（未优化）三种方法进行PMSM转速响应仿真的对比研究，其结果如图5和表2所示。

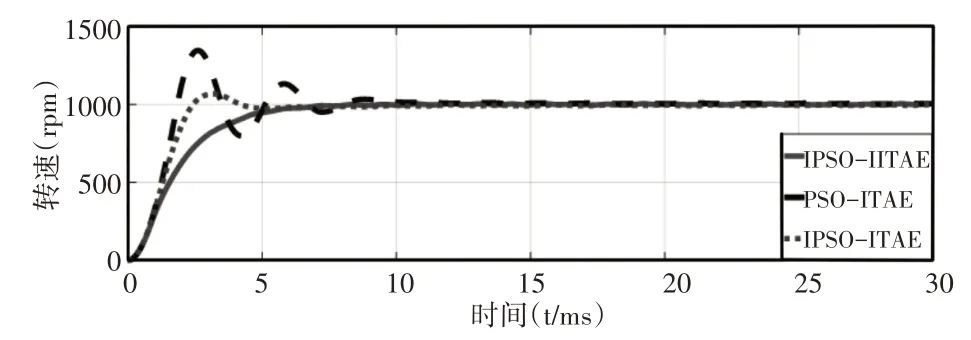
图5 PMSM转速响应曲线Fig.5 PMSM Speed Response Curve

表2 转速响应结果比较Tab.2 Comparisons of Revolving Speed Responses

从图5和表2可以看出，对于在同一ITAE标准下的IPSO控制器所优化的转速环响应，无论是稳定时间还是超调量均大幅优于传统PSO控制器，其超调量减少27.6%，响应速度增加到2.7倍，动态性能明显提高。另外，对于在相同IPSO控制器中，虽然IITAE指标下的稳定时间稍长于ITAE，但是IITAE超调量减少了6.34%。从图5中更直观的看到IITAE指标下电机转速响应能够更稳定的上升。最后根据图1将两电机通过单神经元搭建出IP⁃SO-IITAE单神经元耦合的双PMSM同步控制系统，分别与IP⁃SO-ITAE单神经元耦合和IPSO-IITAE并行控制相比较，其结果如图6与表3所示。可以看出，在相同IPSO单神经元耦合下，通过IITAE指标的同步误差相对于采用未改进的ITAE指标在启动时降低了两电机的同步误差，启动同步精度增加了2.7倍。而在相同IPSO-IITAE下，由单神经元耦合器控制的双电机相较于一般并行控制在受到负载扰动时控制精度从3.18%提升到1.32%，大大提高了系统的抗扰动性能。

图6 转速同步误差曲线Fig.6 Speed Synchronization Error Curve

表3 同步误差结果比较Tab.3 Comparison of Synchronization Error Results

4 实验验证与分析

为验证IPSO-IITAE单神经元耦合对双电机同步控制优化的可行性，利用德国dSPACE的标准组件DS5202作为控制器来搭建实验平台，利用MATLAB∕Simulink∕RTW与dSPACE直接控制两电机，电机为广州德马克电机，其参数如表1，并通过上位机实验软件ControlDesk进行监控与记录。实验原理与环境，如图7所示。

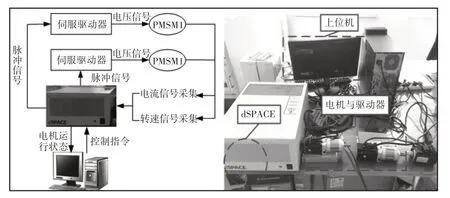
图7 实验原理与环境Fig.7 Experimental Principle and Environment

根据仿真工况与实验条件设置相关参数后进行实验，给定两电机转速为1000r∕min，两电机转速稳定后给电机1施加15N·m的负载扰动，实验结果，如图8、图9所示。

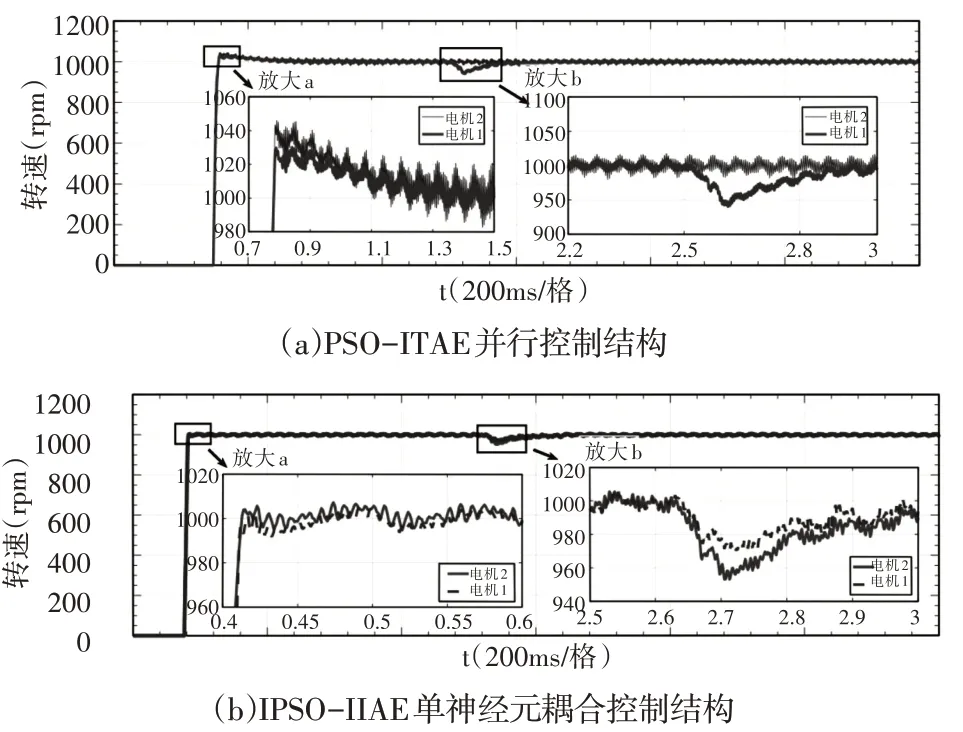
图8 突加负载下的输出转速Fig.8 Output Speed in Sudden Load

图9 两电机同步误差Fig.9 Synchronization Error of Dual-Motor

从图8中可以看到，经过IPSO-IITAE优化后的电机在空载启动阶段降低了超调量，提高了电机的稳态性能。并且通过单神经元耦合器，在电机1受到负载扰动时电机2做出相应转速变化提高了抗扰动性能。综合图8、图9和表4可以发现：在空载启动阶段，超调量减小了3.8%的同时启动同步精度相比增加了2.6倍；在稳定运行阶段，由于IPSO-IITAE和单神经元的共同作用，稳态误差由20r∕min降低到了5r∕min；在系统受到负载扰动时，控制精度从7.6%提升到2.1%，大大增强了系统的抗扰动性能。从以上数据可知，系统通过IPSO-IITAE调节转速跟踪给定，同时通过单神经元耦合器对两电机速度环补偿使其快速同步。因此系统不管在有无负载和空载启动时转速同步误差都得到显著降低，系统表现出优越的鲁棒性、同步性和转速跟踪性。

表4 同步误差结果比较Tab.4 Comparison of Synchronization Error Results

5 结论

针对如何提高两电机的转速同步性能这一问题，提出了一种通过改进的ITAE评价指标下的改进粒子群算法优化速度环PI控制器参数来提高单电机的控制性能，使得转速快速跟踪，并且设计了单神经元耦合器来实现两电机转速同步的实时控制。仿真与实验结果均表明该方法获得了优于标准PSO-ITAE并行控制的整体性能。验证了所提出的控制策略提高启动性、同步性和抗负载扰动性的能力，降低了系统差速震荡的可能。