Flying-V型仓储布局下的拣货路径优化

刘建胜，张 昆，雷兆发

（南昌大学机电工程学院，江西 南昌 330031）

1 引言

随着经济的全球化发展对现代物流行业的服务效率提出了更高的要求，在现代物流中的仓储是一个重要环节，它是集中反映了物资的活动状况，是连接生产、供应、销售的中转站，对提高物流效率起着关键性作用。而在仓库作业中，订单拣货作业是被视为最耗成本和劳动力的一个环节。文献[1]研究发现，订单拣货作业可占到仓库日常作业总量的60%。因此，针对不同的仓库布局，不同的拣货方式中的订单拣货作业的路径优化问题的研究是一项重要课题。而订单拣货所用时间的长短是衡量订单拣货作业效率的重要指，而时间与订单拣货路径密切相关，因此，减少拣货作业行驶的距离可以有效地提高仓库作业的效率。

近年来，针对不同的仓库布局及不同的订单分布情况，文献[2-6]运用遗传算法、蚁群算法等智能算法对仓库中拣货作业路径进行了研究。文献[12]考虑了存储分配策略和订单优化等方面，从而提高了拣货作业效率。文献[7]研究了蚁群算法求解车间配送最短路径问题，取得了良好的搜索效果，表明了改方法能有效的发现最优解。而文献[9]研究了不同仓库布局对拣货路径的影响，他们通过放宽约束，而提出了两种新的布局：Flying-V型布局和Fishbone型布局，Flying-V型布局是对传统布局斜切拣货通道形成的，而Fishbone布局是对Flying-V布局中的指定拣货通道旋转90°形成的。他们的研究证明了在总货位数量相等条件下，与传统布局相比，这两种新布局能使起始点（P&D点）和货物之间的行走距离大约分别减少10%和20%。主要研究在Flying-V仓库布局下的路径优化问题。

2 问题描述

整个的仓库布局平面图，如图1所示。P&D点为仓库的出入口，为了能更好对Flying-V布局仓库拣货路径优化研究，故作出如下假设：（1）拣货员一次拣货作业完成一个订单，不考虑拣货车辆限载问题；（2）忽略拣货员在拣货通道内进行左右两侧货物拣选时行走的距离；（3）拣货员允许在拣货通道折返行走；（4）将仓库布局分成四个拣货区域，货物区域编号顺时针从仓库左下角开始依次为一、二、三、四区。

图1 Flying-V仓储布局Fig.1 Flying-V Storage Layout

2.1 参数设计

图1 中标明了一、二区的排和列的编号顺序，三、四区的排和列的编号顺序是一、二区关于中心线的镜像。在四个拣货区域分别建立了四个虚拟的平面坐标系，使得布局中的每个货位都有唯一的编码，用数组｛K，X，Y｝代表对应的货位编号，其中K（K=1，2，3，4）表示货区号，X（X=1，2，…，Xmax）表示货架的列数，Y（Y=1，2，…，Ymax）表示货架的排数。例如：｛1，5，6｝表示货物位于一区第五列第六排。图1中P&D点记为｛0，0，0｝。研究平面仓库拣选路径，不考虑货位的高度，货位的长和宽设为l，拣货通道和垂直或水平主通道的宽度均为l，斜对角主通道的宽度为2l。

2.2 建立模型

这里研究拣货路径优化问题主要是考虑怎样将一个订单中所有的货物一次性全部拣出，并使其总的拣货路径最优。该类问题类似于旅行商问题。因此结合TSP的数学模型设计了拣货路径问题的数学模型：

式中：S—拣货员完成一次订单拣选作业时总的行走距离；i，j∈Ω—所有待拣选货位以及出发点；i=0—出发点；d ij—货位i与货位j之间的最短距离；u i—拣选点i的拣选顺序（u0=1）；n—拣货点的数量，模型的决策变量是x ij，其取值为：

目标函数式（1）是完成一次订单所行走的最小距离；式（2）和式（3）确保每个拣选点有且只有一个前项和后项任务；式（4）确保拣选路线中不出现子回路；式（5）表示决策变量的取值域。

2.3 计算任意两点之间的距离

因仓库布局存在P&D点，因此计算任意两点间的距离分两种情况：一种是P&D点与任意货位之间的距离，而另一种是任意两货位之间的距离。仅绘制通道的布局简图，如图2所示。

图2 Flying-V仓储布局简图Fig.2 Sketch of Flying-V Storage Layout

（1）P&D点与任意货位i之间的距离：

货位点位于一四区：

货位点位于二三区：

（2）任意两货位点之间的距离：

两货位点在同一区域：

不同通道上：

两货位点在不同的区域分以下几种情况：

当两拣货点在一二区时：

当两拣货点在一三区时：

当两拣货点在一四区时：

当两拣货点在二三区时：

距离计算公式中参数介绍：式中：i，j—待拣选货位；N i—货位i，j的通道编号；K i—货位i的货区编号；S i—货位i，j到拣货通道起始端的距离；L i—货位i，j所在的拣货通道的长度；H—相邻拣货通道间的距离；L—相邻拣货通道截斜对角主通道的长度；S2—拣货通道转至垂直（水平）主通道消耗的距离；S1—拣货通道转至斜对角主通道消耗的距离。

由于Flying-V布局的对称性，两拣货点在二四区的距离公式等同于两拣货点在一三区时的距离公式，而三四区的两拣货公式与一二区的距离公式相同。

3 算法设计

蚁群算法是采用正反馈机制，其使得搜索过程不断收敛，最终逼近最优解。近年来，许多学者致力于蚁群算法的研究，并且成功解决了许多组合优化问题，如调度问题，指派问题，旅行商问题等，都取得了比较理想的实验结果。

3.1 初始化参数

m为蚁群的总数量，n为节点的数量，d ij为节点i到节点j的距离，τij(t)为t时刻节点i与节点j连接路径上的信息素浓度，α为信息素重要程度因子，β为启发函数重要程度因子，Q为信息素释放总量，iter_max为最大迭代数，迭代数初始值设为iter=1。

3.2 构建解空间

将蚂蚁随机地置于不同的出发点，蚂蚁的移动是根据各个节点间连接路径上的信息素浓度来决定其访问下一个城市，P kij(t)表示t时刻蚂蚁k从节点i转移到节点j的概率，其计算公式为：

其中初始时刻，各个节点间连接路径上的信息素浓度相同，设τij(0)=τ0，ηij(t)为启发函数，其值为ηij(t)=1∕d ij表示蚂蚁从节点i转移到节点j的期望程度；allowk(k=1，2，…，m)为蚂蚁k待访问节点的集合。

3.3 更新信息素

在蚂蚁释放信息素的同时，各个节点间连接路径上的信息素也在逐渐消失，以参数ρ(0<ρ<1)表示信息素挥发程度，当所有蚂蚁完成一次循坏后，各个节点间连接路径上的信息素按如下公式进行实时更新：

采用如下的Ant Cycle System模型计算蚂蚁释放的信息素浓度：

4 蚁群算法解决路径优化问题

4.1 算法实现

在仓库拣货过程中，蚁群算法的实现步骤如下：

（1）参数初始化，为了能直观地反应出优化效果，设定仓库中的垂直主通道，水平主通道，拣货通道，货架的长和宽均为1，这里研究随机选10订单，每个订单有30个待拣货点，则n=30，选择蚂蚁数m=50，信息素重要程度因子α=1.5，启发函数重要程度因子β=2，信息素总量Q=50，将m只蚂蚁置于n个顶点上。

（2）更新禁忌表（tabu）和允许访问的节点表（allowed），对每只蚂蚁k（k=1，2…m），按照概率P kij从节点i转移到节点j，将顶点j置于tabu中，而在allowed表中去掉顶点j。

（3）计算蚂蚁行走的路径长度，计算各蚂蚁行走的路径长度L k的值，并记录其最小值。

（4）更新蚂蚁轨迹强度，按更新方程修改轨迹强度。

（5）判断迭代条件，若迭代数iter小于iter_max且无退化行为，则iter=iter+1，转向步骤2。

（6）输出最优解。

4.2 实验仿真

仿真实验的程序采用MATLAB语言设计，程序设计的终止条件即最大的迭代次数iter_max=1000，而其他参数的初始值采用上文中设定的初始值。随机产生一个有30个货位点的订单样本，货位位置信息，如表1所示。

表1 订单中30个货位点及其编号Tab.1 30 Locations and Numbers in Order

图3 蚁群算法路径示意图Fig.3 Path Diagram of Ant Colony Algorithm

图4 传统穿越策略路径示意图Fig.4 Path Diagram of Traditionally Traversal Strategy

图5 S形启发算法路径示意图Fig.5 Path Diagram of S-shaped Heuristic Algorithm

用传统穿越策略，S形启发算法和蚁群算法三种算法分别进行仿真实验，得到的拣货顺序及路径示意图如下：

蚁群算法：

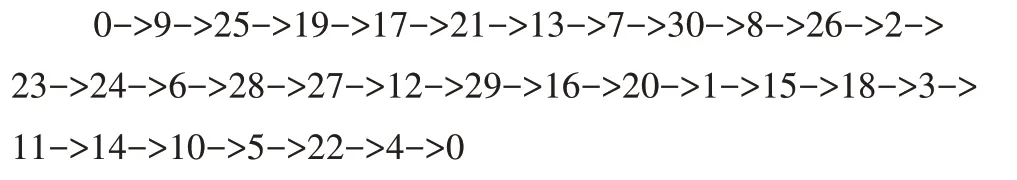
传统穿越策略：

S形启发算法：

三种算法的结果比较，如表2所示。

表2 算法计算结果表Tab.2 Calculating Results of Algorithm

从表2可以看出蚁群算法对路径优化的效果还是比较显著的，为了进一步更全面，准确的反映蚁群算法的优化性能，将随机产生出10个订单，每个订单的货位数为30个，用其上三种算法分别对这10个订单进行实验，实验结果，如表3所示。从实验结果来看，蚁群算法在路径优化上要优于S形启发算法。

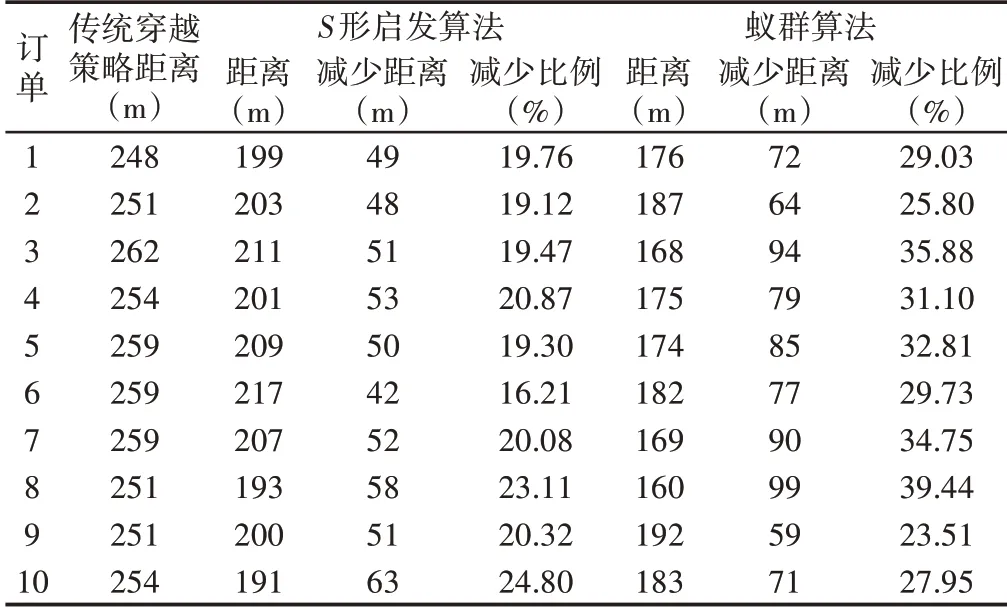
表3 三种算法比较Tab.3 Comparison of Three Algorithms

5 结论

选择合理的拣货路径对于降低物流配送中心运营成本，提高物流效率具有重要作用。通过对flying-V型仓储布局特点建立了路径优化模型，采用传统穿越策略，S形启发算法，以及蚁群算法三种算法进行路径优化，并对结果作了比较，结果显示蚁群算法能更好地解决仓库拣货路径优化问题。