货位指派和拣货路径协同优化及算法研究
方忠民
(中车株洲电力机车有限公司,湖南 株洲 412000)
1 引言
随着电子商务的迅猛发展,客户对订单时效性的要求愈加强烈,为提高拣货效率,增强客户满意度,针对人工拣货系统的优化迫在眉睫。拣货是将商品从其存储位置拣出以满足客户订单要求的过程[1],作为典型的劳动密集型作业,约占整个订单作业劳动力的60%、作业时间的30%-40%[2-5]。在人工拣货系统中,存储商品种类、货位指派策略以及拣货路径策略是影响其拣货效率的重要因素[6-10],而货位指派作为其中最重要的影响因素之一,其优化目标通常是拣货成本(行走路径)最优或拣货时间最短[11]。因此,基于人工拣货系统的货位指派和拣货路径的研究具有重要的实践意义。
现有文献分别从COI[12-13]、需求相关性[14-15]、出货量[16]、周转率[17]以及需求和结构相关性[18-20]等方面对货位指派问题进行了深入研究,但考虑货位指派与其他相关问题协同优化的研究则较少。鉴于此,本文协同考虑货位指派和拣货路径问题并进行研究,目的主要是在拣货员拣货的同时进行货位指派,以此合并作业流程、优化仓库存储结构并进一步提升拣货效率。
2 模型构建
货位指派和拣货路径存在密切联系,以最小化作业周期内拣货总行程时间最短为目标。为不失一般性,做出如下假设:(1)仓库的出入口(Input/Output,I/O)只有一个,拣货员从该处开始拣选并至该处结束作业;(2)不考虑货位的异质性,即仓库中的货位具有相同的尺寸;(3)只考虑低层货架,即每个货架只有一层货位,并以该货位的中心位置作为该货位的坐标;(4)仓库中同一种商品只可存放于一个货位,每个货位只能存放一种商品,也即同一个货位的商品具有同质性,且不考虑仓库缺货情形;(5)巷道为窄巷道,拣货员在巷道内可以方便地拣选该巷道两边货架上的商品,且不考虑商品上下架的时间。在以上假设的基础上,定义模型参数如下:
K—商品编号,数量为qk,索引号为k,k';
N—货位编号,数量qN,索引号为m,m',n。其中m=0表示为I O;
v—拣货员平均行走速度;
Cnt—周期t内货位n可存放商品的数量,其中当n∈时,Cnt取值为1,否则为0;
Jnt—周期t内货位n可拣取商品的数量,其中当n∉时,Jnt取值为1,否则为0;
M—周期t内最大货位调整量;
Pt—周期t内满足订单需求条件的待拣取商品集合;
Qmnt—周期t内拣货员访问完货位m后在访问货位n之前的拣货车容量;
St—周期t内满足货位调整(重新指派货位)条件的商品集合,满足Pt⋂St=∅;

dmn—拣货员从货位m到货位n的行走距离,m,n∈N;
(Am,Bm)—货位m的坐标,(0,0)代表 I O,m∈N;
Wmnt—若拣货员在访问货位m后随即立刻访问货位n,则Wmnt的值为1,否则为0,其中m,n∈N;
Vmt—若货位m在周期t内被访问,Vmt值为1,否则为0,其中m∈N,t∈T;
Dt—周期t内拣货员完成全部任务的总行走距离;
DT—周期t内拣货员完成全部任务的总行走时间。
(2)0-1决策变量
xkmt—若拣货员从货位m处拣取商品k,xkmt的值为1,否则为0,其中k∈Pt,m∈,t∈T ;
yk'm't—若拣货员从货位m'处的拣取商品k'(或将k'商品下架)使其以满足货位调整的条件,yk'm't的值为1,否则为0,其中k'∈St,m'∈,t∈T ;
Zk'nt—若拣货员从货位m'处拣取的商品k'被重新分配存放在货位n处(靠近I O的货位),Zk'nt的值为1,否则为0,其中k'∈St,n∈,t∈T 。
将货位指派和拣货路径进行协同优化的主要目的是为了减少拣货员在寻找待拣选商品时的行走距离,从而提高拣货环节的作业效率,拣货员完成全部任务的总行走距离见式(1)。
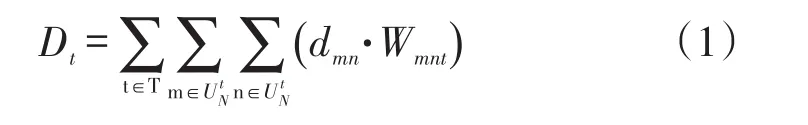
以全部工作时间内拣货员的总行走时间最小为优化目标[27],建立数学模型如下:
目标函数:
约束条件:



其中:t为时间周期;dmn为拣货员从货位m到货位n的行走距离;wmnt为拣货员访问货位m后立刻访问货位n,取值1或0。式(3)表示周期t内拣货员从货位m上拣取商品k以满足订单拣货要求;式(4)表示周期t内拣货员从货位m'拣取需要重新调整货位的商品 k';式(5)和式(6)表示周期t内商品k'被重新指定一个空货位进行存放;式(7)表示若周期t内待调整货位的商品k'被拣货员拣取,则一定可以被重新存储在新的货位上;相反,若周期t内不存在空货位供商品k'存储,则商品k'将不会被拣货员拣取;式(8)表示周期t内商品k为待拣取满足客户订单要求的商品或者满足货位重新指派的商品,不存在商品k既是订单商品又是待重新货位调整的商品;式(9)表示周期t内需要重新进行货位调整的货位数的最大限额,且M小于待拣商品数;式(10)表示周期t内拣货员只访问已经被分配的待拣取商品的货位和重新存放商品的货位(I O除外);式(11)和式(12)表示周期t内拣货员遍历所有任务中已经被分配的待拣取商品的货位和待指派商品的货位(I O除外);式(13)表示周期t内拣货员访问某一货位(I O除外)后,必须离开该货位前往下一货位;式(14)表示拣货员访问货位n后拣货车的容量变化;式(15)和式(16)分别确保拣货员完成任务前后,拣货车容量能够满足订单拣货时的取货商品存放需求和货位调整过程中的商品存放需求;式(17)表示拣货车的最大载货容量。
3 算法设计
3.1 解的编码
利用蚁群算法求解由0-1决策变量xkmt、yk'm't和zk'nt所确定的一条拣货员行走路径。由于协同优化涉及货位指派和商品拣选两个作业环节的协同,要将货位指派和拣货问题转化成能被蚁群行走的点,关键在于要提前处理待重新货位指派的商品,以确定蚁群在去往下一个访问点的路径上是否执行拣货任务(或者货位指派任务)。因此,将问题分为货位指派阶段和拣货路径规划阶段。
在构建货位指派方案方面,用整数0-1表示仓库中的货位属性,0表示空货位,1表示非空货位,构建货位指派方案的可行解集。采用随机生成的方法从可行解中产生初始货位指派方案,并用0-1-2码表示当前货位属性,以0表示待重新货位指派的空货位属性,以1表示待拣取满足订单需求的商品当前所在的货位属性,以2表示待拣取满足重新货位指派的商品当前所在的货位属性,如下所示:
货位编号: 3 91 6 5 810 2 4 7
货位属性1: 1 11 1 0 1 1 0 1 1
货位属性2: 2 11 2 0 1 1 2 1 1
在初始货位指派方案的基础上,采用整数编码方式表示每只蚂蚁所行进的路线。但是由于整条路径的终始点为I O处(以0为编码),则最终路径阶段的个体编码为[0 3 9 1 6 5 8 10 2 4 7 0]。
3.2 路径的构建
3.2.1 生成距离矩阵。假设任意两个货位的坐标分别为 Pm(xm,ym)和 Pn(xn,yn),设dmn为 Pm和 Pn的最短折线距离,则dmn=Xmn+Ymn。其中,Xmn为两货位间最短横向折线距离,即Xmn=|Xm-Xn|。假设ΔYi表示为两货位纵向距离Ymn,ΔY1为拣货员向正北行走的距离,ΔY2为向正南行走的距离,Rm和Rn为仓库货架的排号,Cm和Cn为仓库货架的列号,l为仓库拣货巷道的深度,则Ymn为:

3.2.2 构造可行解。在初始货位指派方案的基础上,采用改进的最近邻点法[27],每只蚂蚁模仿一个拣货员,构造所有拣货路线,其搜索范围由拣货车容量决定,当拣货容量可以满足货位调整时商品临时占用,则从空货位、待拣货货位和待调整货货位的并集中搜索,否则只能从待拣货货位集合中搜索。路线构造完毕后,需进行可行性检验,其可行性需满足的条件为:(1)任意蚂蚁访问了待重新指派货位的商品所在的当前货位点,则必定访问该商品被重新指派的新货位点,反之亦然;(2)任意蚂蚁必须先访问待重新指派货位的商品所在的当前货位点,后访问该商品被重新指派的新货位点,反之不可行。
3.3 转移策略
用一个禁忌表记录该路线中每个时刻蚂蚁所处的位置,并且以该路径的总长度dij作为衡量该路线的评价标准,蚂蚁从出发点开始出发,根据路径上的信息素浓度函数概率,采取轮盘赌法选择其下一个待访问的货位点,直到所有货位点都被访问完。
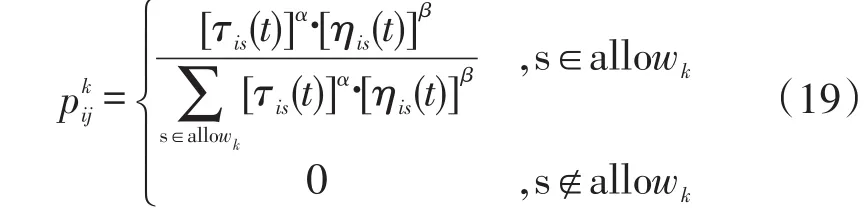
其中,ηis(t)为启发式函数,ηis(t)=1/dij表示蚂蚁从货位i到货位j的期望程度;allowk表示蚂蚁下一步即将访问的货位集合;τis(t)表示路径上的信息量。
3.4 信息素更新
在蚂蚁行走释放信息素的同时,随着时间的推移,其所留信息浓度会不断挥发减少。在经过时间t后,当蚂蚁完成一次循环,各路径上的信息素浓度需要实时更新,其计算方法见式(20)。
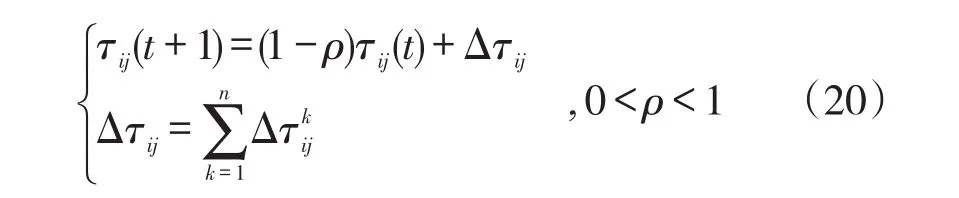
4 实验与分析
4.1 实验方案设计
蚁群算法参数设置为:信息素重要程度参数α=1,启发式信息重要程度β=5,信息素保留率ρ=0.7,蚂蚁个数等于拣货员访问的货位数,启发式因子为拣货员访问各货位间最短行走距离的倒数,仿真实验中采用ant-cycle模型,以随机可行解作为初始解,最大迭代次数为200次。以单区型仓库作为仿真实验的仓库模型,以随机存储策略作为仓库商品的初始货位分配方案,拣货员拣货作业时间以周期t为截止点。假设仓库共有1 200个储位(Pmax=1 200),由20条拣货巷道和2条前后拣货通道组成,每条拣货巷道两边各有10列货架,每条拣货巷道共60个储位,仓库布局参数见表1。
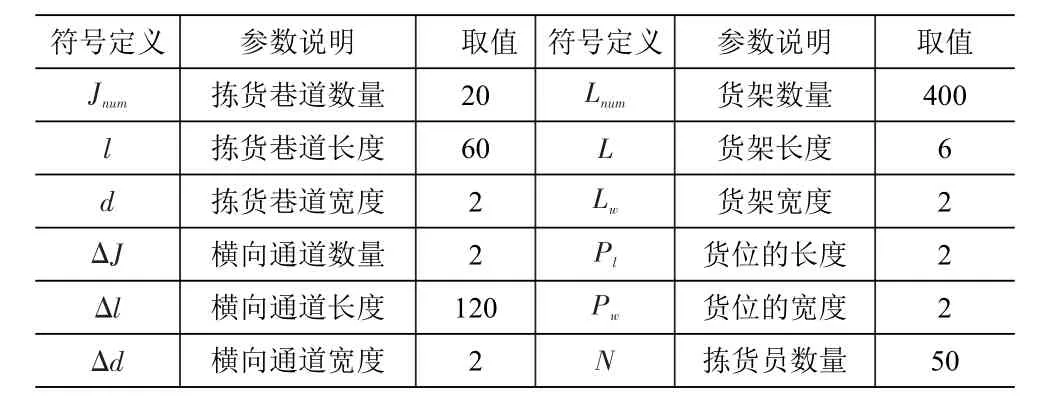
表1 仓库布局参数
4.2 实验结果分析
4.2.1 不同订单规模下的仿真分析。假设周期t内的平均货位调整量n=3,平均订单规模g分别为大(g=60)、中(g=30)、小(g=5,10),根据运行结果得到订单规模大小对优化效果的影响程度,如图1所示。
由图1可知,分别优化和协同优化在订单规模大小不同的情况下存在以下结论:

图1 订单规模大小对优化效果的影响程度
(1)不同订单规模下采用协同优化方法可以改善拣货员在仓库拣货作业过程中的行程时间。
(2)订单规模的大小对拣货行程时间有影响,且订单规模较小时,拣货行程时间改善效果越好。
4.2.2 不同货位调整量下的仿真分析。假设周期t内的平均订单规模g=10(小规模),平均货位调整量n分别为大(n=10)、中(n=5)、小(n=1,3),根据运行结果得到货位调整量大小的影响程度,如图2所示。
由图2可知,分别优化和协同优化在货位调整量大小不同的情况下存在以下结论:
(1)在不同货位调整量条件下,采用协同优化方法仍然可以在一定程度上改善拣货过程中的行程时间。
(2)当订单规模为定值,且为小规模订单时,货位调整量的大小对拣货行程时间有影响;且货位调整量较小时,协同优化方法优于分别优化方法。但当货位调整量较大时,协同优化方法不一定优于分别优化方法。
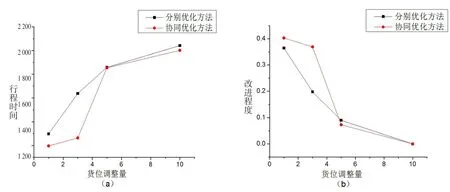
图2 货位调整量大小的影响程度
5 结语
本文以人工拣货系统为研究对象,研究了配送中心的货位指派与拣货路径协同优化问题。以拣货作业总行程时间最短为目标,协同考虑人工拣货系统中的货位指派问题和拣货路径问题,并建立了两者协同优化模型。仿真结果显示,在以人工拣货系统为研究对象,采用考虑货位指派和拣货路径协同优化的方法能够有效地减少整个周期内拣货员总拣货行程时间,并以此提升拣货效率;进一步分析了基于不同平均订单规模下的优化效果以及不同货位调整量的系统优化效果,在平均订单规模较小及货位调整量较小时,获得的优化效果最好,改善效果最明显。

