“球槽模型”中的临界质量比与静止释放初始位置的关系
2021-08-25 04:02:16白荣华李春梅
物理通报 2021年9期
白荣华 李春梅 高 远
(重庆市实验中学校 重庆 401320)
1 问题提出
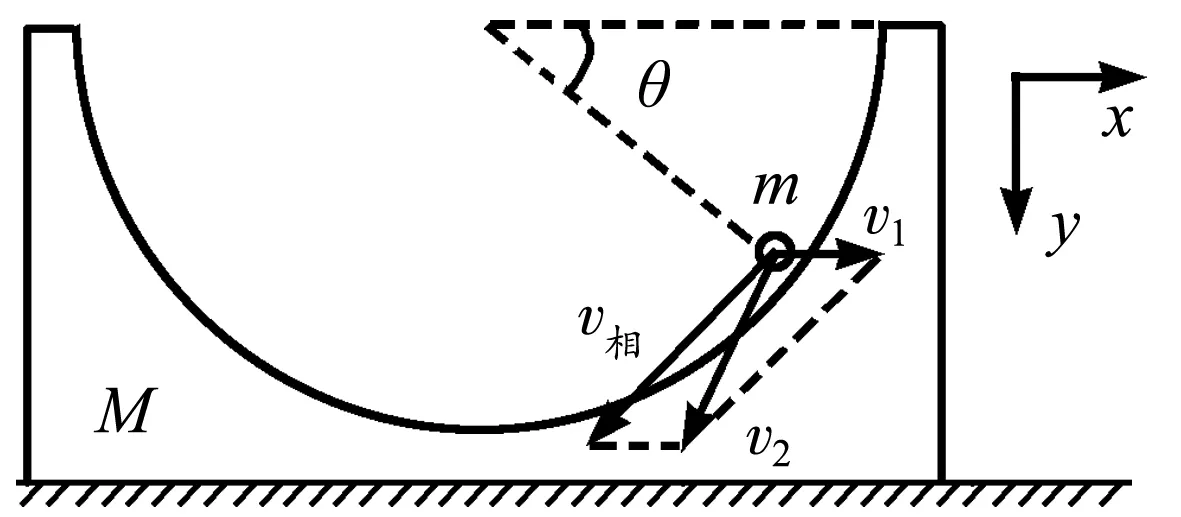
图1 球槽模型
2 数理解析
各量如图2所示,小球滑下后某一瞬时小球与圆心的连线同水平方向的夹角为θ,对球槽系统分别由水平方向动量守恒和机械能守恒定律得
mv2x=Mv1
(1)
(2)
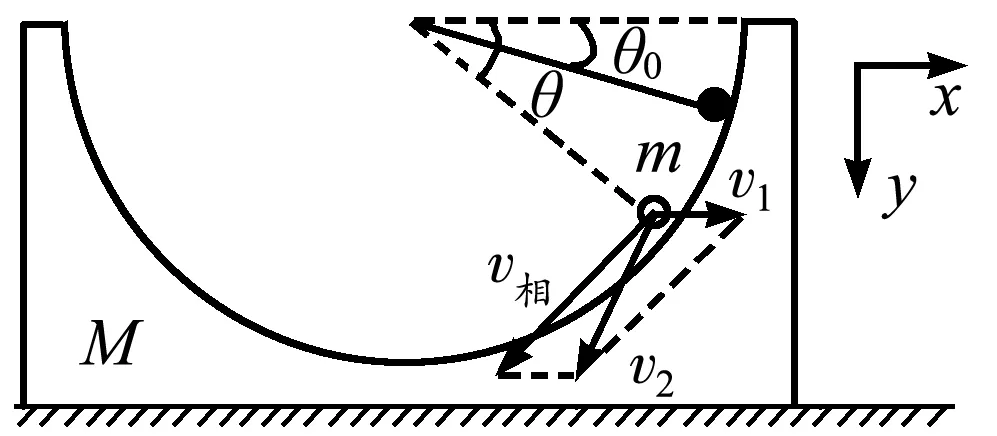
图2 球槽模型各量分析
小球相对槽的速度方向沿圆弧切向,有
v2ytanθ=v2x+v1
(3)
(4)
(5)
v2=
(6)
其中
A=k+k2+(1+k)2cot2θ
为了考查式(6)中球的速率v2的单调性,我们等价考虑下面函数f(θ)的单调性,有
(7)
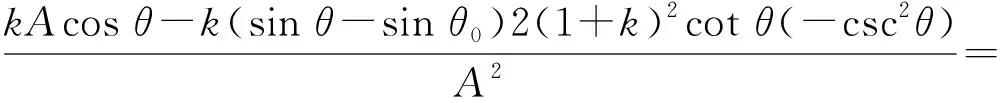
(8)
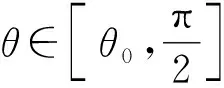
即
(9)
移项后提取公因式有

(10)
两边同乘sin2θ,得
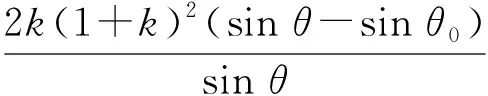
(11)
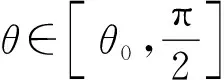
k2(k+k2)≥2k(1+k)2(1-sinθ0)
移项化简得
k2≥2(1+k)(1-sinθ0)
(12)
解此关于k的一元二次不等式,得
(13)
从而得到临界质量比
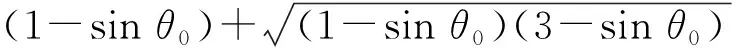
(14)
3 讨论与结论
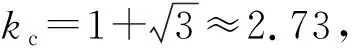

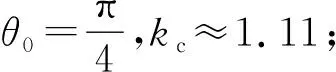
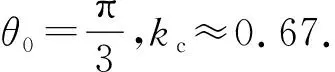

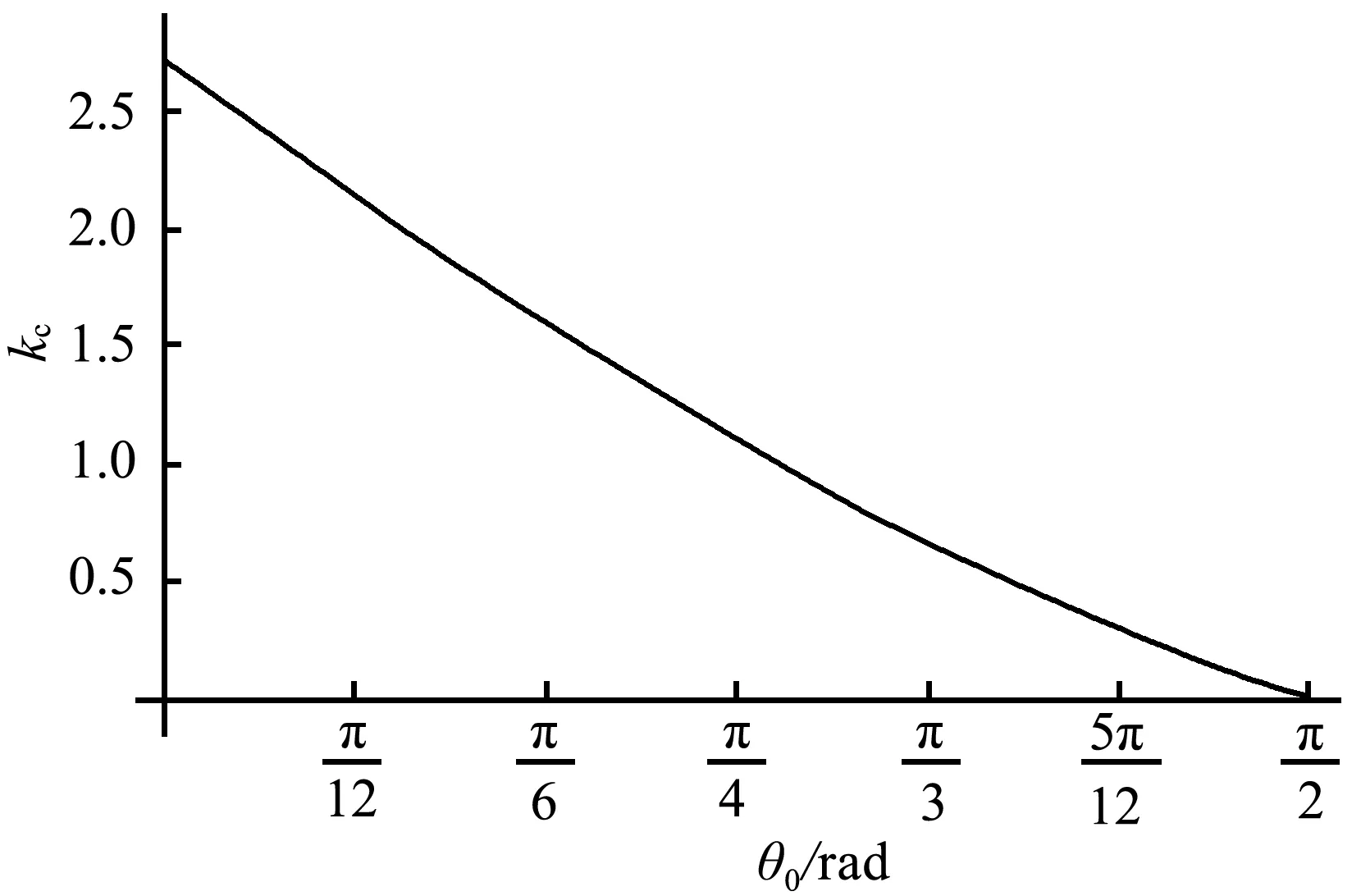
图3 临界质量比kc与释放初始角度θ0的关系
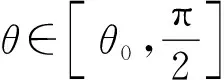
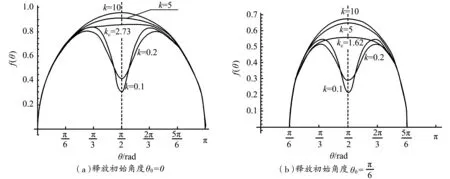
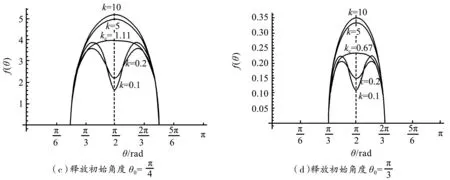
图4 不同释放初始角下,f(θ)随角度变化关系
猜你喜欢
中学生数理化·七年级数学人教版(2023年11期)2023-12-26 08:05:08
小学生学习指导(高年级)(2022年10期)2022-11-04 06:20:50
中学生数理化·七年级数学人教版(2021年11期)2021-12-06 05:38:50
中学生数理化·七年级数学人教版(2020年11期)2020-12-14 06:59:58
中学生数理化·七年级数学人教版(2019年11期)2019-09-10 07:22:44
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:54
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
黑龙江生态工程职业学院学报(2013年1期)2013-12-30 07:49:00
佳木斯大学学报(自然科学版)(2012年5期)2012-09-27 14:26:14

