从“以方测圆”到“化曲为直”
张敏

摘要:在数学教学中融入数学史,可以把教材中呈现的素材和相关史料以知识发生、发展过程的视角进行合理重组,促进学生理解数学本质,领会数学思想,感悟数学文化。HPM取向的《圆的面积》教学,结合史料,依循人类探索圆的面积的发展过程,以学生已有的经验为依托,引领学生“以方测圆”,建立圆面积和正方形面积(r2)的联系;运用数方格法“数”出圆的面积,初步体会极限思想;运用“切西瓜”法“化曲为直”,推理论证。
关键词:HPM;数方格;化曲为直;极限;《圆的面积》
HPM(History and Pedagogy of Mathematics),通常被理解为“数学史向数学教学的渗透”。HPM相关研究表明,个體的认识过程与人类的认识过程基本是一致的,在数学教学中融入数学史,可以把教材中呈现的素材和相关史料以知识发生、发展过程的视角进行合理重组,促进学生理解数学本质,领会数学思想,感悟数学文化。《圆的面积》一课,笔者结合相关史料,开展了HPM取向的教学实践。
一、教学准备
(一)“圆的面积”相关史料
最初,人们认为,圆比较近似正方形,求圆的面积,可以想办法作出一个正方形,使它的面积恰好等于圆的面积。但无论是外切正方形还是内接正方形,都不能满足这个要求。这曾是困扰古希腊数学家的三大几何难题之一。
我国古代数学家刘徽和祖冲之,从圆的内接正六边形出发,让边数成倍增加,单侧逼近圆的面积;古希腊数学家阿基米德,则从内外两个方向双侧逼近圆的面积。这些“以方测圆”思路中的“逼近”就是试图接近“极限”。
古印度数学家则采用“切西瓜”的办法:把圆切成许多“小瓣”,再把这些“小瓣”平均分成两部分,各自展开后,拼插成一个近似的平行四边形,用这个近似平行四边形的面积去代替圆的面积。后来,德国天文学家开普勒也仿照“切西瓜”的方法,大胆地设想把圆分割成无穷多个小扇形,圆的面积就是无穷多个小扇形面积的和。开普勒断言(但无法证明):无穷小的扇形可以看作三角形,扇形面积等于三角形的面积。显然,这种方法对人类的想象和推理提出了挑战,是极限思想的雏形。
(二)HPM取向的《圆的面积》教学思路
尽管历史上人类探索圆的面积的方法不同,但不同中蕴藏着相同——都希望“化曲为直”,即把圆这个曲边图形转化为直边图形;而且在解决问题的具体过程中,每种方法都不可避免地涉及“无限接近”——这也是历史上讨论最为激烈的焦点问题。
因此,《圆的面积》一课教学,可结合史料,依循人类探索圆的面积的发展过程,以学生已有的经验为依托(如求不规则图形面积的“数方格”法、求取面积公式的“转化”策略等),引领学生“以方测圆”——将圆的面积与正方形的面积建立联系,给圆的面积确定一个范围;“求精入微”——思考并想象,当用来做单位面积的方格变得越来越小,直至无穷小时,就可以准确地“数”出圆的面积了;“化曲为直”——采用“切西瓜”的思路探寻圆的面积计算公式。这样的过程中,学生充分经历猜想、操作、验证、讨论和归纳等,在层层深入的活动中体会“转化”和“极限”思想。
二、教学过程
(一)在画圆中唤醒已有经验
师同学们,你们会画圆吗?老师给大家准备的学习单上有个方格图,请拿出圆规在上面画一个圆。
(学生在学习单上画圆。)
师谁能用学过的知识介绍一下你画的圆。
生我画的是半径3 cm的圆。
生我画的是直径4 cm的圆。
生我画的是周长25.12 cm的圆。
师通过大家的介绍,可以看出同学们从不同方面对圆有了一定的了解。根据以前学习平面图形的经验,你们还对圆的什么知识感兴趣?
生圆的面积。
师(板书课题:圆的面积)今天我们就来学习圆的面积。请同学们猜一猜,圆的面积大小可能跟什么有关?
生半径。
生直径。
生周长。
[说明:通过在方格纸上画圆以及对圆的自主介绍,唤醒学生已有的经验,促其提出问题,引发思考,并自然地将圆的面积与半径、直径甚至周长建立联系,为后续教学新知做好准备。]
(二)了解古埃及“以方测圆”的思路
师圆的面积计算这个问题,其实是古希腊三大几何难题之一,古代人很早就开始思考了。(播放视频,画面定格于图1)古埃及人对于圆面积的探究,是借助于其与正方形面积的关系来进行的。参考古埃及人的思路,大胆猜测一下,与一个圆有着密切联系的正方形在哪儿?
生以圆的半径为边长的正方形。
生以圆的直径为边长的正方形。
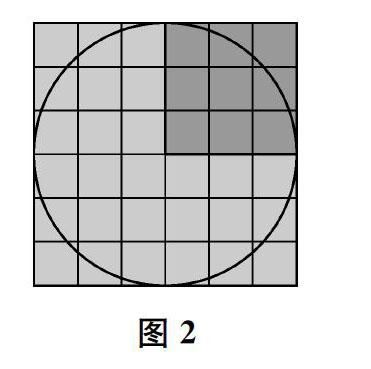
师(出示图2)同学们的感觉很敏锐!深入思考下去,估一估,圆的面积和这两个正方形的面积相比怎么样?
生圆的面积比小正方形面积的2倍大一些。
师你是怎么想的?
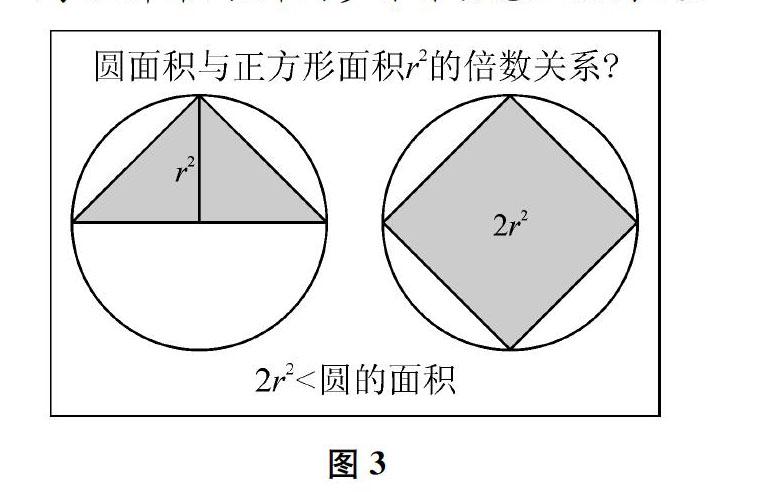
(学生解释,教师同步课件动态呈现图3。)
生圆的面积比大正方形的面积小一些。
生大正方形面积是小正方形面积的4倍,说明圆的面积比r2的4倍小一些。
(学生解释,教师同步课件呈现图4。)
[说明:介绍古埃及人探究圆的面积的史料,将圆的面积与正方形的面积建立关联,引导学生利用方格图中与圆的半径和直径关系最密切的2个正方形(以半径为边长和以直径为边长),估计出圆的面积的大致范围:2r2<圆的面积 (三)化用古埃及“数谷粒”的方法“数圆” 师同学们对圆面积的大小确定了一个合理的范围。当然,仅有范围还不够,得想办法把它们确切的倍数关系弄清楚。想一想,在方格图中计算不规则图形的面积,有什么经验可以借用?
生可以用数方格的方法。
师好,我们就用数方格的方法来研究圆的面积到底是r2的几倍。先把正方形的面积,也就是半径的平方数出来,是多少?
生9平方厘米。
师数圆的面积有什么好的建议吗?
生只要数出四分之一圆的面积,然后乘4就可以了。四分之一圆大约是7.5格,圆的面积大约是30平方厘米。
师拿出计算器算一下,圆的面积大约是r2的几倍?
生保留一位小数,大约是3.3倍。
师同学们,为了使我们的实验数据更有说服力,请大家拿出自己上课开始时画的圆,数出它的面积,算算面积是r2的几倍,把结果记录下来,等待汇报。
(学生活动后汇报数据,汇总得到表1。)
表1正方形面积与圆面积的倍数关系
正方形面积
(r2)圆面积圆面积大约是正方形面积的
几倍(精确到十分位)9303.316523.225783.1361123.1师请同学们仔细观察表格,你有什么发现?
生圆的面积都是r2的3倍多一些。
师这就比刚才估测的范围更精确一些了。我们把数方格的方法和古埃及人数谷粒的方法联系起来看看。(播放视频,画面定格于图5)看到3.14倍,大家就想到了什么?
生π倍。
师我们用实验的方法,通过大量的实验数据发现,圆的面积是r2的π倍。
[说明:数是度量的一种基本策略。这种策略指向了度量的数学本质,也有利于学生实现经验的迁移。首先,引导学生利用研究不规则图形面积的“数方格”经验,将自己所画圆的面积数出来,并将其与r2的倍数关系算出来。通过不同的数据对比,进一步确定:圆的面积大约是r2的3倍多一些。结合史料介绍,用均匀分布的小格子代替谷粒,当小格子足够多时,数方格得到的圆的面积大约是r2的3.14倍。这个环节,将学生已有学习经验与史料中古埃及人的探索方法相结合,通过数、算的过程将圆的面积与r2之间的倍数关系进一步精确化。特别地,引发学生思考并想象,当用来做单位面积的方格变得越来越小,直至无穷小时,就可以准确地测量出圆的面积了。借助课件,帮助学生经历直觉的“极限”过程,初步理解“极限”。]
(四)运用古印度的“切西瓜”法“化曲为直”
师在数学研究中,实验数据确实可以说明问题。不过,大家都知道,最严密、最有说服力的方法还是——推理。同学们,以前我们在研究一个新的图形的面积时,是怎样推导的?
生把新图形用剪拼的方式转化成学过的图形,化未知为已知,利用新旧两个图形间的关系进行推导。
师(出示图6)那今天我们学习的圆,能转化成我们学过的图形来研究吗?
(学生交流。)
师大家提出了一些方法。现在来看看古印度数学家的思路。(播放视频,画面定格于图7)是不是跟我们刚才有的同学的思路相同?我们下面来试一试这种方法。老师给各组同学准备了不同的学具,请大家沿着圆的半径剪开,看能不能拼成熟悉的平面图形。
(学生分组剪接,并贴到黑板上。)
师比较一下大家剪拼出来的图,有什么发现?
生随着份数的增加,拼出的图形越来越接近平行四边形。
师同学们,设想一下:如果平均分的份数更多,分成64份、128份、256份……这个图形会怎么样?
生应该会完全接近平行四边形。
生会完全接近长方形。
师德国天文学家开普勒也仿照“切西瓜”的方法,大胆地设想把圆分割成无穷多个小扇形。开普勒断言:无穷小的扇形可以看作三角形,最终拼出来的图形就是长方形。我们可以借助电脑来模拟这样的过程。(用“几何画板”软件演示圆平均分成64份、128份、256份、512份、1 028份……的情况)你们有什么感受?
生把圆平均分成无数份的时候肯定是拼成长方形了。
师比较一下,圆与拼成的长方形存在哪些关系?能不能根据长方形的面积计算方法推导出圆的面积公式?
生长方形的面积和圆的面积相等;长方形的长相当于圆的周长的一半c2,它的宽相当于圆的半径(r),长方形的面积等于长乘宽,所以圆的面积可以用圆周长的一半乘半径。那么,圆的面积公式就是S=πr×r=πr2。
(教师同步板书推导过程。)
师推理的结果和刚才由实验数据得到的结果一致:圆的面积是r2的——π倍。这样我们就十分肯定地得出了圆面积的计算方法。
[说明:“化曲为直”是全课的中心环节。通过丰富的活动,一方面,使学生体会圆的面积与r2的倍数关系,用“数方格”法得出结论后,更要以推理的方式加以验证,亦即数学结论的得出过程应该是从猜想到实验验证再到推理证明的科学过程,将合情推理与演绎推理相结合,培养学生严谨的科学态度和理性精神;另一方面,则是将学生的“转化”经验迁移到新知中来。结合史料中古人的探索,组织学生在亲自动手操作,进一步积累经验的基础上,通过想象活动深刻感受“极限”思想。整个过程中,努力将学生的已有经验与人类的探索过程无缝对接,使他们真正经历“再发现”“再创造”过程。]
(五)回顾梳理历史研究轨迹
师同学们,现在你能算出开始的时候自己所画的圆的面积了吗?动手算一算。
(学生运用公式计算后交流。)
师大家把算出来的面积与之前数方格得到的面积比一比,有什么感受?
生根据公式计算出的数据比较精确,数方格得出的数据有误差。
师回顾一下今天的研究過程,我们是怎么得出结论的?
生先是猜测圆的面积与半径的平方有倍数关系;然后估一估,发现圆的面积是半径平方的2倍—4倍;接着数一数,通过实验数据发现圆的面积是半径平方的3.14倍;最后通过剪拼,将圆转化成长方形,成功推导出了圆面积的计算公式,确定了圆的面积是半径平方的π倍。
师总结得很好!我们借鉴了古人的智慧,结合了自己学习平面图形面积的经验,沿着历史的足迹,经历了一个数学结论得出的完整过程。刚刚有同学问我:圆被平均分成若干份之后,那些小扇形还能拼成其他的平面图形吗?课后大家不妨去剪一剪、拼一拼、想一想、算一算,相信你一定会有更大的收获!
[说明:得出圆的面积计算公式后,让学生准确计算出课始自己所画圆的面积,并与之前数方格得到的面积数据进行对比,体会数学的精确性及应用性。引导学生回顾整节课的研究过程,让学生体会到自己在课堂上经历了人类千年的探索过程,帮助学生在感受数学文化的同时,体验数学探索的“逐步精确化”。最后,引发学生对圆的面积公式其他推导方法的深入思考,为今后的学习研究奠定扎实的基础。]
参考文献:
[1] 郑玮,郑毓信.HPM与数学教学中的“再创造” [J].数学教育学报,2013(3).
[2] 王晓军,汪晓勤. HPM视角下的“图形旋转”问题探究[J].数学通报,2012(5).
[3] 陈金飞.独到的,才是不可替代的——HPM 视角下对“圆的面积”的思考与教学实践[J].江苏教育,2015(17).
[4] 弗赖登塔尔.作为教育任务的数学[M].陈昌平,唐瑞芬,等编译.上海:上海教育出版社,1995.

