基于数字化学习平台的小学数学计算教学实施

摘要：小学数学计算教学存在“一教就懂，一做就错”的现象。其原因有算理不明、教学要求过于一致、练习评价比较粗略等。对此，尝试利用数字化学习平台，打破课堂的物理空间，满足不同学生的学习需求，为每一个学生提供针对性指导，从而提升计算教学的效益。通过实践，形成了一定的教学范式：创设需要计算的问题情境;搭建探究算理的“脚手架”;收集探究算理的过程;交流探究算理的成果;完成个性化的计算练习。

关键词：小学数学;计算教学;数字化学习;教学范式;个性化学习

计算是小学数学的重要内容领域。然而，很多教师深深感到计算教学“一教就懂，一做就错”。根据调研分析，笔者认为其原因主要有三。一是算理不明。算理就是“为什么这样算”，是计算的依据。日常教学中，教师给予学生明晰算理的空间不足，又缺乏一定的工具帮助学生理解，使得很多学生在计算时只会依葫芦画瓢地“死算”，知其然而不知其所以然。二是教学要求过于一致。班级授课制下，教师教学更多地采用“齐步走”策略，对全体学生用同一标准，没有提供不同的学习路径，使得想“跳一跳”的学生没有平台，想“补一补”的学生没有空间。三是练习评价比较粗略。计算练习中，教师一般采用校对答案、同桌互批的形式粗略了解学生的学习情况，因而对哪些学生有哪些错误很难把控，特别是对学生错误的思维过程无法知晓，使得评价反馈（基于评价的教学）的精准性不高。

针对以上问题，基于计算教学的特点，我们尝试利用数学化学习平台，打破课堂的物理空间，满足不同学生的学习需求，为每一个学生提供针对性指导，从而提升计算教学的效益。通过实践，我们形成了一定的教学范式。下面，以苏教版小学数学三年级下册《两位数乘两位数的笔算》一课为例，谈一谈这一教学范式的具体实施。

一、创设需要计算的问题情境

很多学生不喜欢数学，是因为长期以来数学在他们头脑中形成了晦涩、难懂，与现实生活格格不入的印象。华罗庚先生也说过：“人们对数学产生枯燥无味、神秘难懂的印象，原因之一便是脱离实际。”计算教学应该创设真实的问题情境，激发学生学习的兴趣和计算的需要。这一点，当下各版本的小学数学教材都给了比较好的范例。而借助数字化学习平台，可以创设更加生动、开放的问题情境。

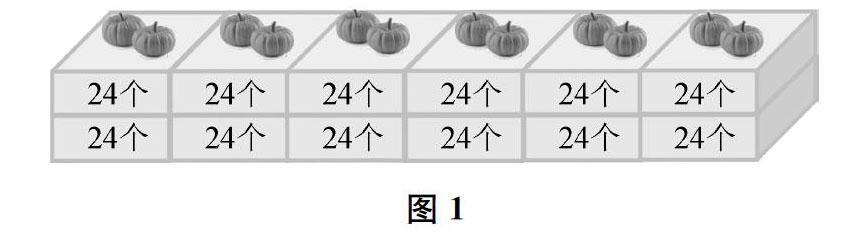
《两位数乘两位数的笔算》一课，教师通常基于教材例題，提供一张12箱迷你南瓜的图片（如图1所示）作为情境，让学生寻找其中的信息，发现计算问题：一共有多少个南瓜？而利用数字化学习平台，可以把静态的12箱南瓜转变为可拖动的一箱箱南瓜。这样，情境就更加生动、更加开放了，为学生的自主探究提供了更加强大的动力和更加广阔的空间：学生可以根据自己的经验，像做游戏一样，自由拆分和组合12箱南瓜。

二、搭建探究算理的“脚手架”

建构主义学习理论指出，学习不是由教师把知识简单地传递给学生，而是由学生自己建构知识意义的过程。当学生面对陌生的计算问题时，教师不能简单告知计算方法，而要让学生自主探究计算原理，从而得到计算方法。尤其是班级授课制下，不同的学生探究的结果很可能不同，这就为学生通过交流扩展视野、提升认识奠定了良好的基础。考虑到自主探究时学生可能遇到困难，并且不同的学生有不同的学习基础，教师可以搭建不同的“脚手架”，启发不同学生的思路。而借助数字化学习平台，可以更加方便地提供更为丰富的学习素材和工具，从而更好地搭建“脚手架”。

《两位数乘两位数的笔算》一课，学生已经学过两位数乘整十数和两位数乘一位数的计算。学生列出算式24×12后，教师可以利用数字化学习平台，提供如下探究算理的“脚手架”，供不同的学生选择：

（1）想想自己已经学过哪些类型的计算，将南瓜箱分堆，分别计算。

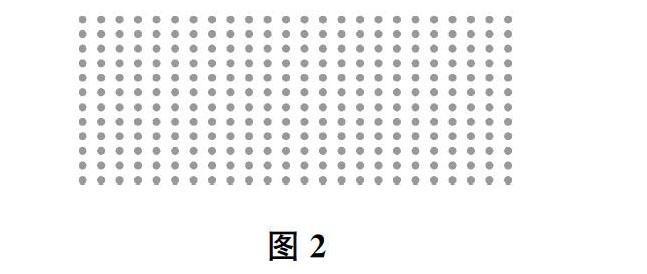
（2）想想自己已经学过哪些类型的计算，在如图2所示的点子图（每个小圆点代表一个南瓜）上圈一圈，再算一算。

（3）先观看微视频，再想办法算一算。微视频中，首先出现12箱南瓜的不同分法，包括“10箱和2箱”“9箱和3箱”“8箱和4箱”“7箱和5箱”“6箱和6箱”“4箱、4箱和4箱”等;在每一次分的过程中，动态呈现“南瓜图”抽象成“点子图”的过程。

对此，抽象思维能力较强的学生可以选择第一个“脚手架”（甚至不用拖动南瓜箱）;形象思维能力较强的学生可以选择第二个“脚手架”;前面两种路径都解决不了的学生就可以选择第三个“脚手架”，借助微视频中更充分的提示展开自主探究。

三、收集探究算理的过程

在问题情境和“脚手架”的引领下，学生便可自主探究算理，经历个性化的学习过程。对此，教师要给学生充足的探究时间，同时可以借助数字化学习平台，全面、高效地收集、理解学生的探究过程——如果没有数字化学习平台，教师通常就只能通过巡视，片面、低效地发现、了解学生的学习情况。

《两位数乘两位数的笔算》一课，学生探究算理时，教师要求学生借助平板电脑的录屏功能把探究过程记录下来并上传到数字化学习平台。由此，教师通过数字化学习平台对学生的探究过程进行收集和理解，将其分为如下三类：

（1）学生在数字化学习平台上拖动南瓜箱，分堆计算，具体的几种情况如下页表1所示。

表1学生分堆计算南瓜个数的具体情况

序号分堆计算1把12箱南瓜分成2堆，每堆6箱24×6×2=288（个）2把12箱南瓜分成3堆，每堆4箱24×4×3=288（个）3把12箱南瓜分成2堆，分别是10箱和2箱24×10+24×2=288（个）4把12箱南瓜分成2堆，分别是9箱和3箱24×9+24×3=288（个）5把12箱南瓜分成2堆，分别是8箱和4箱24×8+24×4=288（个）（2）学生在数字化学习平台上圈点子图计算，具体的几种情况如图3—图6所示。

（3）个别学生用竖式计算，如图7所示。

〖4〗24×12〖4〗48〖3〗240〖3〗288

四、交流探究算理的成果

全面、高效地收集、理解学生探究算理的过程后，教师便可对比呈现典型的探究成果，组织学生进行结构化交流，以扩展学生的视野，提升学生的认识。在数字化学习平台的帮助下，呈现的探究成果会具有更好的直观性和动态性，更加便于理解。在此之前，可让学生自由地查看和点评其他同学的探究成果，初步了解其他同学的想法，打开自己的思路。在数字化学习平台的帮助下，这样的学生自由交流既广泛、又便捷，能为后续教师呈现典型探究成果的交流奠定良好的基础。

《两位数乘两位数的笔算》一课，学生自主探究算理、初步交流成果后，教师便利用数字化学习平台，对比呈现几个典型的探究成果，组织两个层次的结构化交流：

首先，教师呈现表1第1行、表1第3行、图3、图5四个探究成果，引导学生比较它们的相同点和不同点。学生不仅发现了第一、第三个探究成果和第二、第四个探究成果分别具有相同的本质，而且感受到了从实物图到点子图再到算式这一不断抽象的数学建模过程。

其次，教师呈现图7（竖式）这个探究成果，引导学生思考这种做法与刚才几种做法的联系和区别。学生发现了表1第3行、图5和图7三个探究成果本质上是相同的，而形式上表现出从具体到抽象、从横式到竖式的变化，从而理解了两位数乘两位数笔算的算理，建构了相应的算法。

五、完成个性化的计算练习

应用练习可以帮助学生巩固所学内容、检验学习效果，是新知教学必不可少的环节。在班级授课制下，新知探究的过程受到教学任务的制约，即使借助数字化学习平台，也很难实现全面精准的个性化学习（只能实现分层粗略的个性化学习）。而应用练习的过程受到的制约比较少，选题的范围比较宽，借助数字化学习平台的题库出题、即时评价功能，可以实现全面精准的个性化学习。尤其是计算教学中，计算练习的设计和评价（以及基于评价的再设计）都相对比较简单，也就更容易借助数字化学习平台来完成。

一般来说，计算教学中，教师可以利用数字化学习平台，设计基础、变式和综合三个层级的应用练习，并在学生完成后即时评价反馈。对于基础练习，如果学生全做对了，就由平台自动呈现变式练习;如果学生出现错误，就由平台提醒学生改正，改正之后，再由平台根据错误的类型提供相应的跟进练习帮助学生强化，然后，也由平台自动呈现变式练习。对于变式练习，教师可以设计“小锦囊”，给有困难的学生一些提示。同样地，如果学生全做对了，就由平台自动呈现综合练习;如果学生出现错误，就由平台提醒学生改正，改正之后，也再由平台自动呈现综合练习。此外，学生在每个层级的应用练习中产生的错题，会由平台自动汇总到错题库中，每个学生都会形成自己的错题库，整个班级也会汇总得到一个更大的错题库。由此，后期每个学生都可以有针对性地进行练习，教师也可以有针对性地设计练习。整个过程如图8所示。

《两位数乘两位数的笔算》一课，笔者设计的三个层级的计算练习如下：

【基础练习】

计算：12×23、14×33、44×22。

【变式练习】

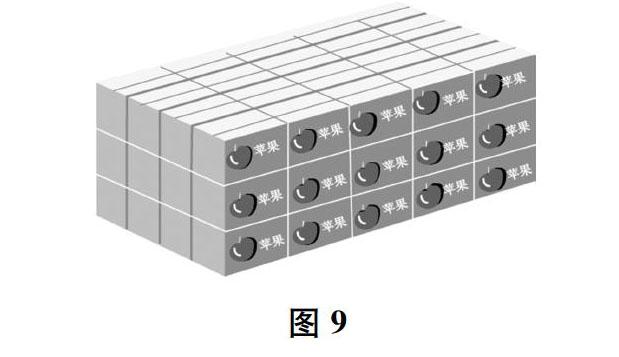
1.如图9所示，一共有多少箱苹果？

2.我们班四个组的同学分别是10人、11人、12人、12人。如果每个同学每天捡12个白色垃

圾，你能算一算自己所在组的同学每天一共捡多少个白色垃圾吗？

【综合练习】

通过观看微视频学习“铺地锦”的乘法计算方法，然后用竖式和“铺地锦”两种不同的方法计算：14×21、22×32、24×13。

三个层级的计算练习从无情境到有情境（分别是图形情境和生活情境），从用本课学习的方法到用拓展学习的方法，难度不断提升，让学生在变式中，巩固理解算理，熟练掌握算法。在完成基础练习的过程中，部分学生出现进位错误，所以，数字化学习平台提供了4×9+5、6×7+9、8×8+7、5×9+6这样一组口算题作为跟进练习，有针对性地帮助他们突破乘加进位的难点。

最后，需要指出的是，上述教學流程的架构和数字化学习平台的使用虽然相对来说更适合于计算教学，但是也可用于小学数学其他类型的新授教学，一般只需做些微调。

*本文系江苏省教育科学“十三五”规划重点自筹课题“小学数学教学中开展数字化学习的实践研究”（编号：Bb/2018/02/117）的阶段性研究成果。

参考文献：

[1] 潘小福.课型范式与实施策略：小学数学[M].南京：江苏教育出版社，2012.

[2] 潘小福，蒋敏杰.小学数学数字化学习的深度思考与实践推进[J].教育研究与评论（小学教育教学），2017（2）.

[3] 丁志根.基于校本实践的数字化学习实施策略[J].小学数学教育，2018（24）.