基于模糊PID的升降机层门联动装置建模与仿真研究*

赵秉鑫,卢 宁*,鹿开旭,张洪伟,刘雪岩

(1.北京建筑大学 机电与车辆工程学院,北京 100032;2.河北建设集团股份有限公司,河北 保定 071000;3.北京理工大学 机械与车辆学院,北京 100081)

0 引 言

升降机的联动装置是用于同步开启笼门与层门到达设定位置的装置,由一个三相异步电机驱动,通过传动机构完成开关门的动作。

在其联动装置的传动过程中,圆柱直齿轮、蜗轮蜗杆以及链轮、链条机构存在齿侧间隙和啮合误差等非线性因素,影响了其传动的平稳性和精度[1]。在工业控制领域中,对联动装置传动的控制常常用到常规PID控制方法,但这种方法在非线性系统控制方面难以达到满意的效果。为了保障被控对象达到控制目标,需要设计一种非线性控制器来控制联动装置[2]。

针对非线性系统难以建立准确数学模型的问题,蒋晨迪[3]采用了ADAMS与MATLAB联合仿真的方法,建立了虚拟仿真平台,实现了对新型扶梯制动器控制系统的仿真。冷华杰[4]利用机电联合仿真平台对火炮系统中齿轮传动存在的非线性因素进行了研究。

目前,发展较为成熟的非线性PID控制器的种类有神经网络PID、模糊PID、专家PID等[5]。周围[6]设计了一种模糊PID控制器,提高了对送杆机构非线性系统的控制效果。熊中刚[7]采用神经网络整定PID控制器,实现了对平地机非线性时变系统的精确控制。杨立秋[8]提出了一种专家PID控制器,在消除船用起重机的非线性摆动方面取得了良好效果。

部分学者提出的控制器,虽然可以实现对非线性系统的精确控制,但其数学模型与控制算法复杂,难以满足施工升降机联动装置的实际控制需求。因此,本文设计一种模糊PID控制器,利用机电联合仿真技术进行仿真分析,验证控制方案的合理性。

1 联动装置结构分析

1.1 机械结构

该联动装置包含:三相电机、蜗轮蜗杆减速器、圆柱直齿轮、传动轴、单排链轮、防脱链板、配重块、滚珠丝杠螺母、直线导轨、层门拨块、机架等,其联动装置传动简图如图1所示。

图1 联动装置传动简图

联动装置的工作原理为:由三相电机输出动力,电机轴带动蜗杆转动与蜗轮相啮合,将动力输出给传动轴,传动轴上布置大齿轮与两个单排链轮;大齿轮与小齿轮通过啮合传递动力,带动丝杠旋转,使螺母作直线运动,完成对层门的开关动作;两个单排链轮与链条啮合,完成笼门的开关动作。

笔者采用SolidWorks软件,对联动装置的各个零部件进行参数化建模,简化与本次研究无关的零部件。联动装置三维模型如图2所示。

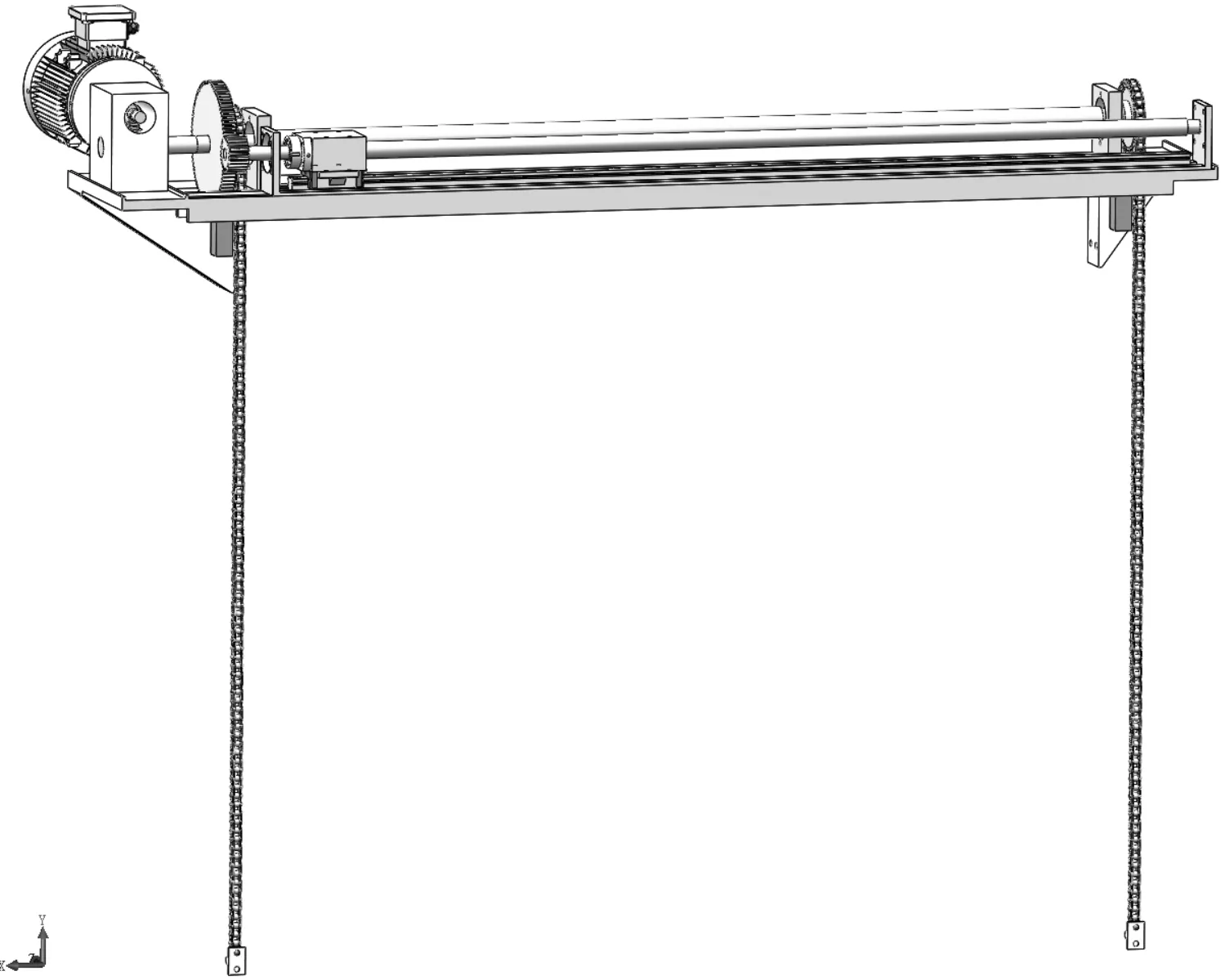
图2 联动装置三维模型

1.2 控制系统

根据联动装置的控制要求,确定控制系统硬件。控制系统硬件主要包括PLC、通用变频器和编码器。该控制系统以层门为控制对象,由PLC控制器控制。

联动装置控制系统原理框图如图3所示。

图3 联动装置控制系统原理框图

控制信号为层门运动的位移信号,编码器安装在丝杠末端,用于检测丝杠转速。通过公式推算得到层门的位移为:

(1)

式中:n—丝杠转速;Ph—丝杠导程。

笔者将误差与误差变化率作为模糊PID控制器的输入,通过查询嵌入在PLC中的模糊控制表整定KP、KI、KD参数,输出模拟量信号,调节通用变频器的输出频率和电压,控制电机转速,进而控制层门拨块的线位移,达到对层门运动的半闭环控制。

2 联动装置系统建模

2.1 通用变频器的数学模型

在工程实际中,通常将采用恒压频比控制方式的变频器的传递函数简化成为惯性环节[9],即:

f=Kfur

(2)

式中:f—变频器输出频率;Kf—变频器增益系数;ur—变频器输入模拟量电压。

电机额定输入电压UN为:

UN=KNfN

(3)

式中:fN—电机额定输入频率;KN—变频器增益系数。

Uc=K1f=KNKfur

(4)

故变频器的传递函数为:

(5)

式中:K1—电压频率转换系数;T1—时间常数(变频器频率变化时间)。

变频器参数如表1所示。

表1 变频器参数表

2.2 三相电机的数学模型

建立三相异步电机的数学模型通常需要忽略空间和时间谐波、磁路饱和以及铁心损耗的影响[10]。接下来讨论基于恒压频比控制方式的三相电机数学模型的建模过程。

根据电机正常工作状态下的近似等效电路,折算到定子侧的转子电流表达式为:

(6)

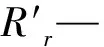
根据机电能量转换关系得到电机的电磁转矩为:

(7)

式中:Pm—电动机电磁功率;ωm—同步电磁角速度。

忽略励磁电流,即C1≈1,将简化后的式(6)代入到式(7)得:

(8)

式中:np—电机磁极对数。

(9)

根据电机的参数可得转子每相电阻为:

(10)

根据运动平衡方程,可得:

(11)

将式(9)代入式(11),得到转速与输入电压的微分方程为:

(12)

式中:J—负载折算到电机轴的转动惯量;B—粘滞阻尼系数;TL—负载转矩。

三相异步电机参数如表2所示。

表2 三相异步电机参数表

在MATLAB/Simulink模块中建立的变频电机仿真模型如图4所示。

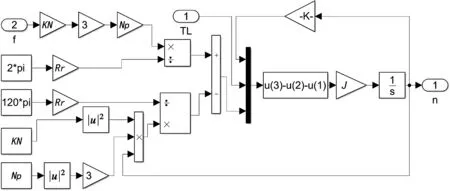
图4 变频电机仿真模型

2.3 联动装置的动力学模型

在蜗轮蜗杆、圆柱直齿轮与链轮链条的运动过程中,由于外界因素和自身结构的特点导致啮合不平稳,使得传动不均匀,很难建立准确的非线性动力学模型。因此,要在ADAMS中建立传动机构的虚拟样机,准确地模拟啮合接触的过程。

传动机构动力学模型的相关参数主要由其自身尺寸、材料属性、实际工况等决定,根据相关公式及推荐参数得到参数设定值。

动力学模型接触参数设定值如表3所示。

表3 动力学模型接触参数设定表

笔者采用ADAMS中Hertz接触理论的Impact模型确定接触点的法向接触力,其函数表达式为:

(13)

式中:K—接触刚度系数;δ—两物体接触渗透深度;e—刚度指数;dmax—最大阻尼完全作用距离;Cmax—最大阻尼。

根据Coulomb摩擦方法来计算接触点切向接触力,其函数表达式为:

Fs=-Fn·step(v1,-Vs,-1,Vs,1)·
step(|v1|,Vs,fs,Vd,fd)

(14)

式中:v1—相对滑移速度;Vs—最大静摩擦相对滑移速度;Vd—动摩擦相对滑移速度;fs—静摩擦系数;fd—动摩擦系数。

在各个零部件之间添加约束,联动装置动力学模型系统拓扑,如图5所示。

图5 联动装置动力学模型系统拓扑图

联动装置动力学模型如图6所示。

图6 联动装置动力学模型

2.4 联动装置的控制系统模型

机电联合仿真控制系统如图7所示。

图7 机电联合仿真控制系统

引入模糊PID控制策略对层门进行位置控制,层门位移的误差信号通过模糊PID控制器进行调节,设定通用变频器输入模拟量的饱和信号模块(即对模拟量输入限幅),模拟PLC通过D/A转换输出0～10 V的模拟量信号来控制变频器的输出电压,根据西门子PLC中PID的算法原理,在MATLAB/Simulink中建立离散PID模块[11]。设定变频电机输出转速的饱和信号模块(即对输出转速限幅)。在ADAMS中建立一个状态变量(即电机转速)作为输入;3个状态变量(即负载力矩、层门位移和层门直线运动速度)作为输出,完成对控制系统模型的建立。

3 模糊PID控制器

目前,因其控制性能和控制复杂性相对较好,二维模糊控制器得到了广泛应用[12]。在该控制系统中,以层门拨块的理论位移与实际位移的误差量E和误差变化率EC作为模糊控制器的输入,通过模糊控制器输出参数ΔKp、ΔKI、ΔKD,对传统PID控制器的参数进行整定,以适应复杂的控制模型。

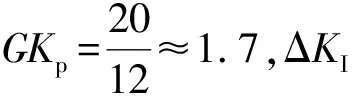
ΔKp的模糊规则如表4所示。

表4 ΔKp的模糊控制规则表

ΔKI的模糊规则如表5所示。

ΔKD的模糊规则如表6所示。

表5 ΔKI的模糊控制规则表

表6 ΔKD的模糊控制规则表

采用Mamdani模糊推理方法[15，16],得到各个输出参数的模糊控制规则曲面。

ΔKp模糊控制规则曲面如图8所示。

图8 ΔKp模糊控制规则曲面

ΔKI模糊控制规则曲面如图9所示。

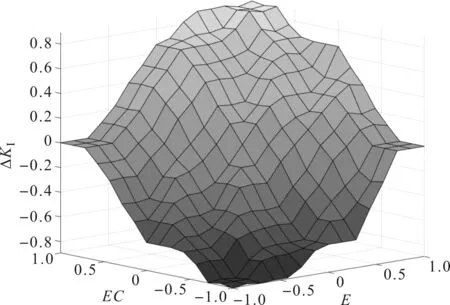
图9 ΔKI模糊控制规则曲面

ΔKD模糊控制规则曲面如图10所示。

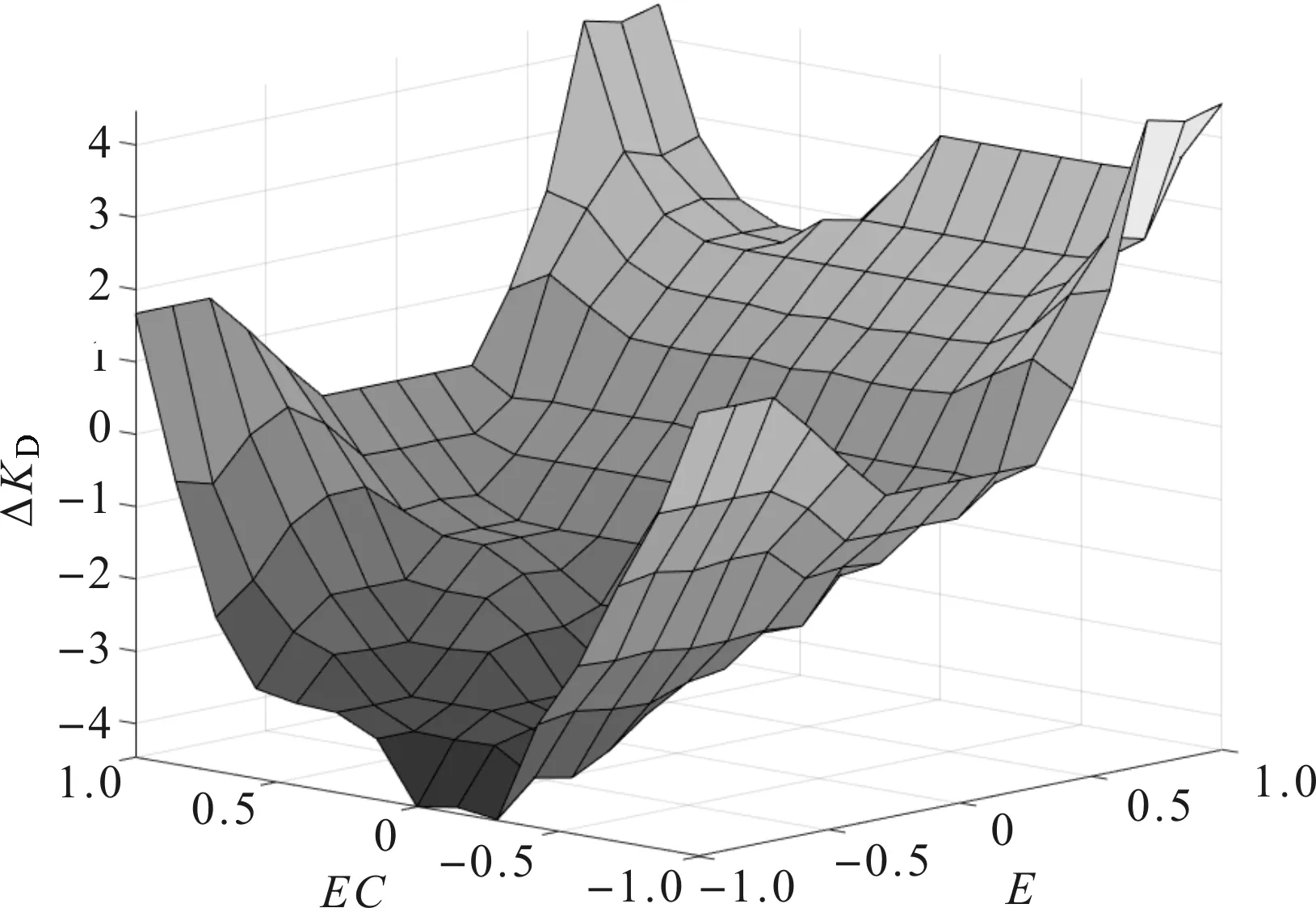
图10 ΔKD模糊控制规则曲面

4 控制系统仿真

笔者采用MATLAB/Simulink与ADAMS联合仿真的方法对升降机联动装置的控制系统进行仿真,采用工程上整定PID参数的方法对PID的KP、KI、KD进行初步确定。

控制系统仿真参数如表7所示。

表7 控制系统仿真参数表

在控制系统的两种工况下,分别对给定控制信号的响应进行仿真分析。

控制系统跟踪工况一位移信号的响应曲线如图11所示。

图11 控制系统跟踪工况一位移信号的响应曲线

图11中,设定层门的开度为1.3 m,层门的位移控制信号采用S-Function进行编写;设定层门在t=1 s时刻以0.32 m/s速度开始匀速运动,在t=5 s时刻运动停止,到达目标位置。

控制系统跟踪工况一位移信号的误差曲线如图12所示。

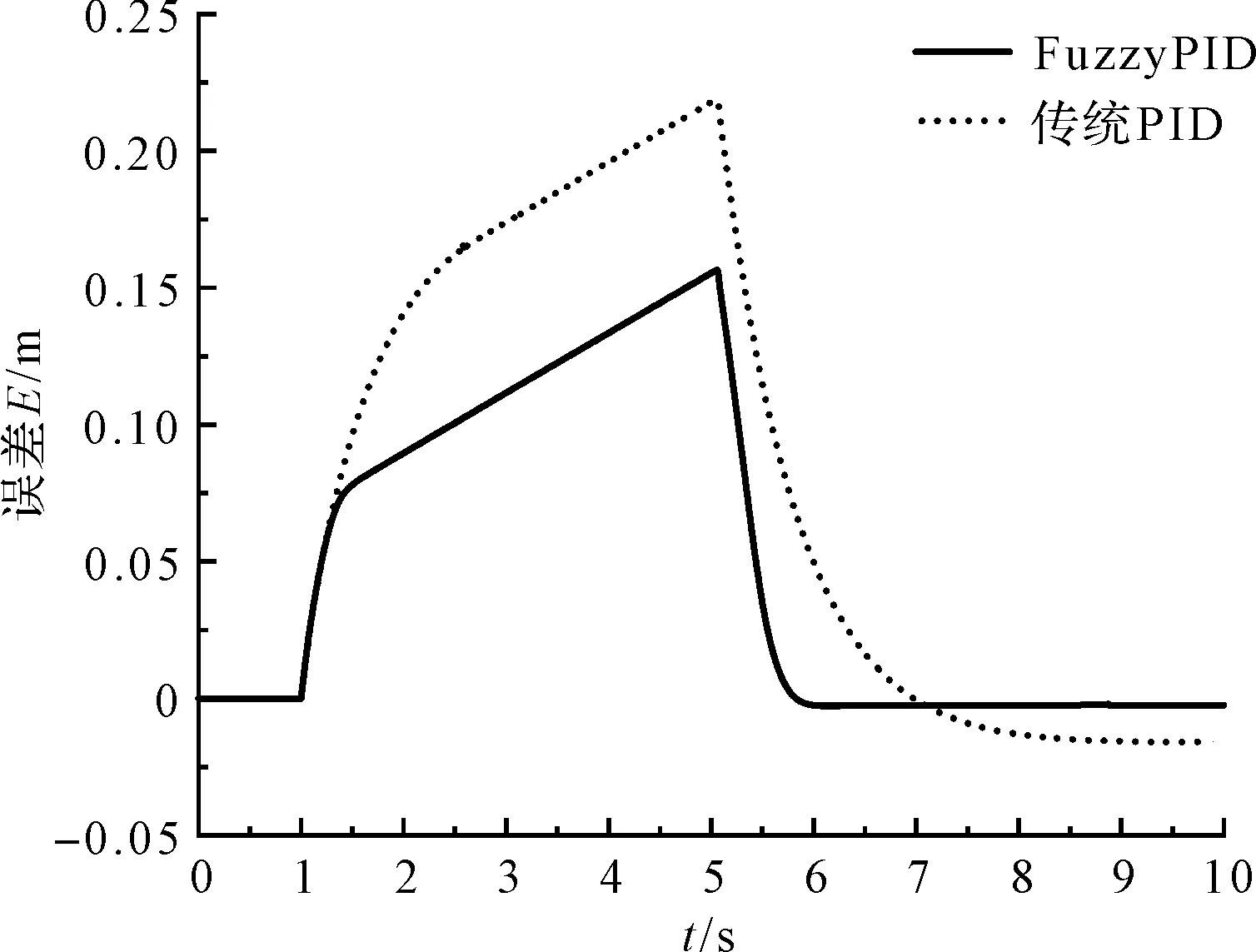
图12 控制系统跟踪工况一位移信号的误差曲线

图12中,在传统PID控制下,控制系统的最大误差为0.223 m,控制系统的稳态误差为0.016 m,采取模糊PID控制后,控制系统的最大误差为0.158 m,控制系统的稳态误差为0.002 m;系统的最大误差下降了29.2%,稳态误差下降了87.5%。

结合图11和图12可以看出,模糊PID对位移信号的跟随性优于传统PID,控制精度得到提高。

控制系统跟踪工况二位移信号的响应曲线如图13所示。

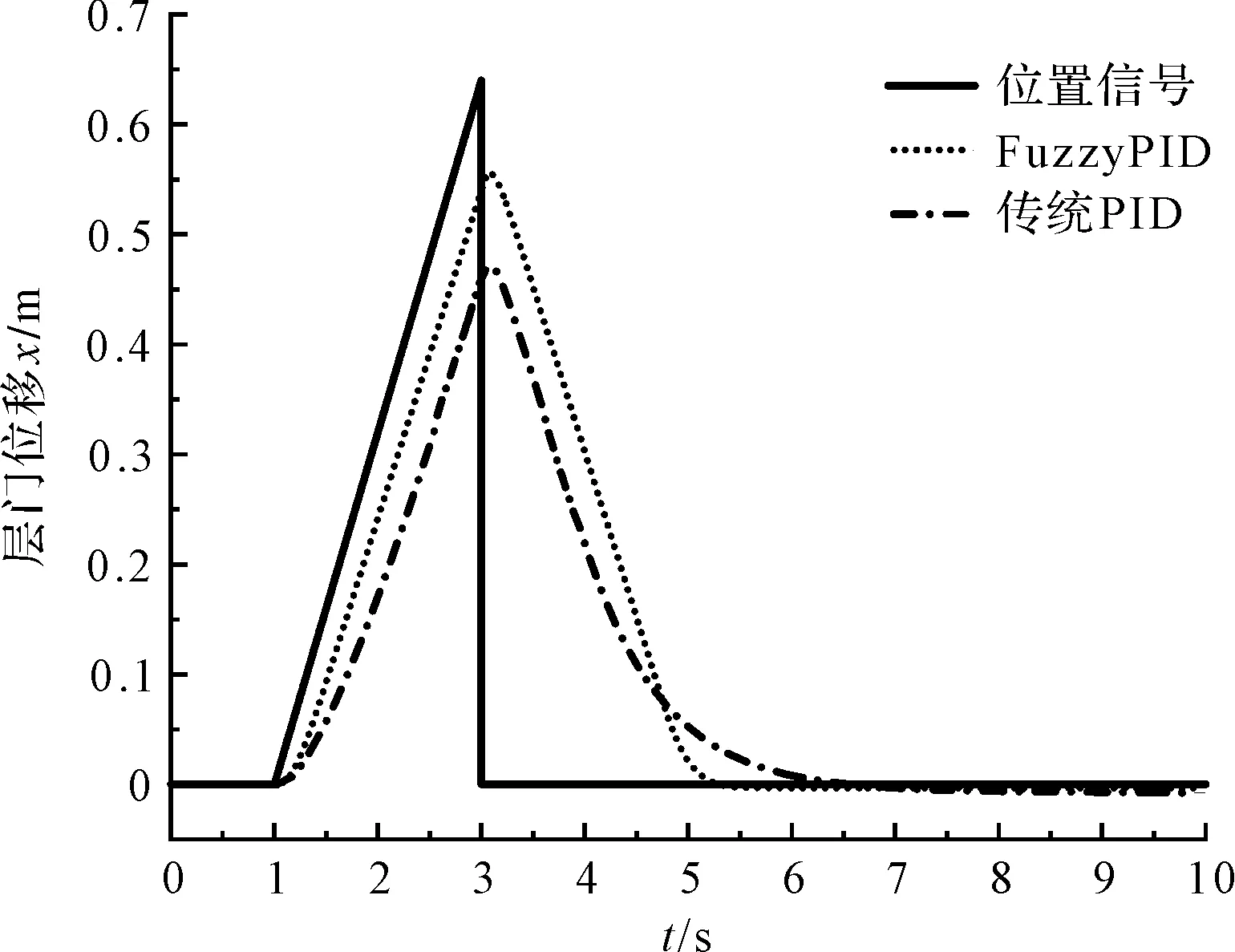
图13 控制系统跟踪工况二位移信号的响应曲线

图13中,出于安全考虑,在层门运行过程中发现危险情况时,需要对处于运行状态的层门发出立即归位的操作指令,设定层门在1 s

通过仿真结果可以看出:在传统PID控制下，跟踪阶跃信号的过程中,系统的调节时间为3.3 s;模糊PID控制下，跟踪阶跃信号的过程中,系统的调节时间则下降至2.1 s,系统的响应速度提升了36.4%。

因此,相比于使用传统PID控制器,模糊PID控制策略在跟踪系统突变信号方面的能力明显提升。

5 结束语

本文对升降机的联动装置的原理和结构进行了分析,建立了通用变频器与变频电机的数学模型,及传动机构的动力学模型和控制系统模型;采用MATLAB/Simulink与ADAMS机电联合仿真的方法,对升降机联动装置的控制系统进行了仿真分析。研究结果表明:

(1)在工况一下,相较于传统PID控制器,模糊PID控制器对给定信号的跟随性能更好,系统的最大误差下降29.2%,稳态误差下降87.5%;

(2)在工况二下,相较于传统PID控制器,模糊PID控制器对给定信号的响应速度更快,系统的响应速度提升36.4%;

(3)采用模糊PID控制策略提升了系统的控制精度,满足了联动装置的控制要求。

今后,笔者将在升降机联动装置物理样机上做进一步的研究,并对设备进行更好的现场调试。