局部近似平面V型沟槽减阻特性数值模拟研究*

徐 琰，张 臣，汪子轩

（南京航空航天大学，南京210016）

为了适应未来航空发展的需求，飞行器正向大推重比、高速、高续航能力等方向发展，然而随着全球环保意识的不断增强，对耗油率也提出更高要求。在民用客机飞行时，摩擦阻力和诱导阻力占总阻力的绝大部分。目前，减阻技术研究的重点都是致力于减小这两种阻力，民用客机注重燃油经济性，即使阻力降低1%也能给航空公司带来相关可观的经济效应[1]，因此减阻技术一直是整个航空界的研究焦点。

为了减少物体表面的摩擦阻力，许多湍流边界层控制方法被提出，根据是否需要额外能量介入，可以分成主动控制减阻和被动控制减阻两类。这两种方法又以不同的减阻理论为标准进行了分类，如图1所示。

图1 减阻技术分类Fig.1 Classification of drag reduction techniques

由于主动控制减阻技术需要外部输入能量才能实现减阻，在追求可持续化发展的今天，在实际工程应用中可行性较低，仍停留在试验研究阶段，多是为了探究湍流猝发的机理。而非光滑表面减阻技术因其具有不添加任何外部能量和装置，仅通过改变自身表面结构就能够实现减阻效果的特性，能够有效控制成本，满足未来可持续发展需求，一直是减阻领域的一个重要研究热点，具有重要的理论意义与工程实用价值[2]。

非光滑表面减阻技术是一种通过改变物体表面微尺度结构，达到减阻效果的被动控制手段。它首次由美国NASA 研究中心的Walsh 提出，通过对鲨鱼皮表面结构的研究，发现鲨鱼皮表面的顺流向微小肋条结构可以有效地降低壁面的摩擦阻力，该成果打破了光滑表面阻力小的传统思维。Huang 等[3]从湍流边界层角度对微织构进行了研究，并在机翼表面覆膜，降低了7%的阻力。Martin 等[4]对间断的纵向肋条进行研究，发现纵向肋条能有利于阻隔涡的横向发展，减小了剪切应力的产生，从而减小了阻力。Choi[5]在边界层减阻机理的探索过程中发现，沟槽表面可以减少近壁区边界层的速度脉动，在风洞试验中表明，在20～100Hz 的范围内，沟槽结构可以显著减小壁面脉动压力。Bixler 等[6]将微织构布置在封闭管道中，分别以流体流速、流体黏度和微织构的几何形状为变量进行试验，结果表明微织构结构可以减小流动过程中的压降，实现减阻。国内在非光滑表面减阻性能的研究起步较晚，南京航空航天大学潘家正[7]将不同尺寸及间距的沟槽结构横向布置于平板，并在风洞中进行试验，得到10.2%的减阻量，基于对流动状态及雷诺数的分析，提出了“微型空气轴承”理论，认为横置沟槽改变了流体流动状态，并在沟槽内部形成涡结构，充当“微型空气轴承”的作用，实现减阻。戎瑞等[8]采用数值计算方法，在NACA0018 翼型上布置脊状结构，分析了脊状结构对翼型边界层速度分布和尾迹速度分布的影响，发现在翼型前端布置脊状结构，可以提前边界层分离点，并提前结束分离区域，而在后段布置脊状结构，提前分离点的同时，还有效控制了边界层分离，增加了升力，减小了阻力。Zhang 等[9]利用有限元分析方法，提出了一种确定微织构布置位置的方法。在叶片表面布置微织构，与光滑叶片相比具有减阻效果，优化了叶片的气动性能。刘梅等[10]采用大涡模拟，探究沟槽结构引起的熵产变化规律，发现沟槽结构能够有效减小近壁区总熵产，为沟槽减阻优化提供理论依据。

经过多年的研究，减阻微织构的发展还存在一些问题： （1）部分学者们总结出一套采用将微织构尺寸无量纲化来进行微织构高度设计的方法，然而该方法只能针对平面，在曲面中的应用较少，对于曲面的适应性并未进行深入研究；（2）很多学者从边界层角度研究具有减阻效果的微织构高度问题，对于微织构的其他几何特征参数如位置、宽高、数量等多是通过试错法，得出减阻效果较好的结论，对设计原理未做过多分析，特征参数对微织构减阻效果的影响规律不明确。因此本文采用离散的方法，将复杂曲面分成局部小平面研究，探究微织构在局部小平面上的减阻特性，基于边界层理论提出一套微织构的高度和位置设计方法，并在小平面表面布置不同形状、深度、宽度、间距的V 型沟槽结构，利用计算流体力学方法模拟小平板表面的气流流动，探究各种特征参数对于V 型沟槽在小平面上的减阻效果影响。

1 减阻微织构设计

许多学者发现，微织构的减阻效应主要与边界层有关，因此本文的减阻微织构的设计主要基于边界层理论，通过外部流场的流速以及绕流物体的特征尺寸，并对尺寸进行无量纲化，确定近壁区边界层过渡层范围，从而确定特征高度和位置参数范围，利用仿真手段对结构参数进行优化，最终确定最优参数，如图2所示。

图2 减阻微织构设计流程Fig.2 Design flow of drag reduction microtexture

1.1 基于边界层的微织构设计方法

绕流流场可以划分为边界层和外流区两个部分，图3是流体在平壁上的流动情况，流体速度在壁面上为0，然后沿壁面法线方向y不断增加并最终达到来流速度u0。按普朗特的边界层概念，将速度从u=0 到u=0.99u0对应的流体层厚度为边界层厚度，用δ表示。而边界层内的横向流动也分为层流与湍流两种形态。如图4所示的平壁扰流流动中，在平壁的前部，边界层内的层流向后部的湍流过渡。

图3 边界层及边界层厚度Fig.3 Boundary layer and boundary layer thickness

图4 边界层内的流动形态Fig.4 Flow patterns in boundary layer

在湍流区域，自由流的动能被转化为湍流波动，然后通过黏性作用耗散为内能[11]。在壁面区域边界层中大部分湍流动能产生于黏性底层、缓冲层和对数律层，如图5所示。

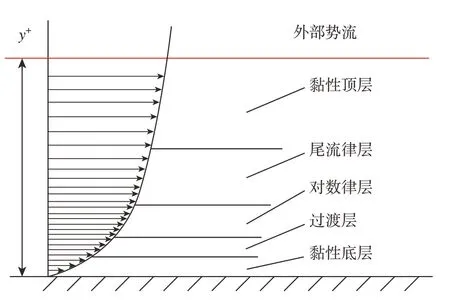
图5 湍流边界层的各层分布示意图Fig.5 Distribution diagram of each layer of turbulent boundary layer

边界层区域是根据壁面的无量纲距离y+确定的。其中，y是距离壁面的量纲距离；v为运动黏度；uτ为壁面应力剪切速度。

通常近壁区在y+≤100 的范围内，其中黏性底层0≤y+≤5，黏性切应力为主导，湍流切应力为0。过渡层5≤y+≤30，黏性切应力和湍流切应力同时存在。对数律层30≤y+≤100，湍流剪应力占主导[11]。

1.2 尺寸无量纲化

为了方便根据边界理论进行微织构设计，微织构几何形状尺寸通常采用无量纲化的参数。主要考虑微织构的高度h、宽度w和间距s，如图6所示。

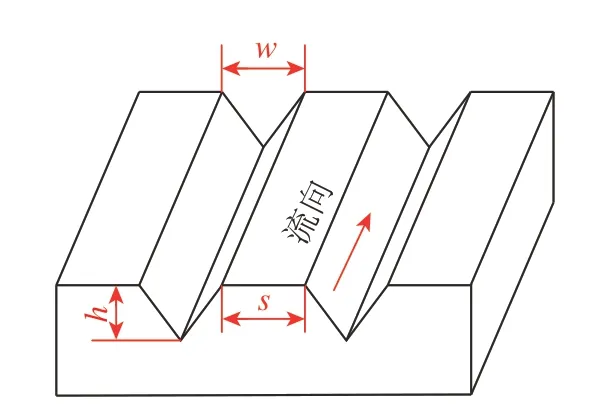
图6 微织构参数Fig.6 Parameters of microtexture

其中，s为微槽间距；h为沟槽高度；w为沟槽宽度；μ为动力黏度；v为运动黏度；u为管内平均流速；uτ为壁面应力剪切速度；τ0为壁面剪切应力；ρ为密度。

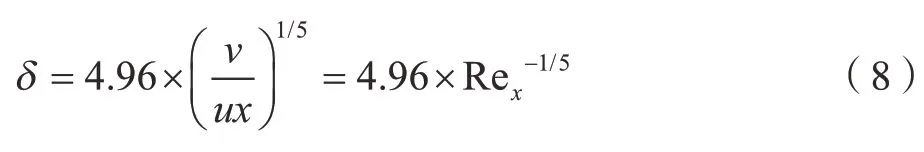
将式（9）带入式（7）得：

将式（10）带入式（5）得：

将式（11）带入式（2）～（4）得：

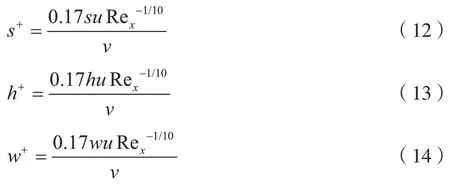
2 数值模拟方法及验证

2.1 曲面分区域分析数值模拟方法

本文对沟槽微织构进行仿真，并对其仿真结果进行对比分析，探究沟槽微织构的减阻特性。由于物体表面曲面各异，为使减阻效果最大化，单一的微织构无法适应全局，因此将曲面分成局部小平面讨论，由于曲面上流动情况复杂，将曲面分成几个局部平面单独考虑，前后的边界条件无法用简单的FLUENT 命令进行描述，针对这一问题使用FLUENT 中profile 命令来实现，如图7所示，将计算域1 进行计算，计算完成提取出口条件，并导入到计算域2 中作为入口边界条件，从而实现局部平面到完整曲面的过渡，可以有效降低计算成本，并使微织构减阻效果最大化。

图7 曲面到局部平面Fig.7 Surface to local plane

2.2 计算域模型建立及网格划分

为了同时对比具有微织构的表面和光滑表面的阻力，将两种平板放置在同一个计算域内进行仿真。以V槽为例，计算域如图8所示。光滑面在计算域顶部，沟槽面在底部，底部沟槽条数统一为10 条，为避免仿真过程中上下边界层相互干扰，计算域高度设置大于10 倍的沟槽深度，本次仿真中，最大沟槽深度为0.5mm，因此高度设为5mm。针对局部平面，选取小尺度计算域，本文中计算域长度设为5mm。

图8 计算域Fig.8 Computational domain

本文采用ANSYS 基于工作流的网格划分方法，划分的网格是非结构网格，截面为六边形，具有高质量，且在壁面具有边界层划分方式，能够使网格按一定比例增长。如图9所示，第一层网格根据边界层理论对应主y+=1，对应的高度为0.0124mm。以1.2 的比例递增，直至网格尺寸为0.5mm，以保证能够准确地捕捉壁面处的流动状况，提高计算精度。

图9 微织构网格划分模型Fig.9 Microtexture meshing model

2.3 湍流模型及边界条件

由于雷诺平均法具有较好的计算精度，同时计算成本较低，因此本文采用Realizablek–ε两方程湍流模型，结合Ehanced wall treatment 近壁面处理，在求解计算域中心的湍流区域的同时，也能很好地处理近壁面区域的低雷诺数的流体，选用二阶迎风格式对方程进行离散，采用simple 算法进行迭代计算。

计算域在流体流动方向上的边界条件为周期边界条件，采用流量入口，定义左右为对称边界，上下边界为无滑移壁面边界条件，流体为空气，空气密度ρ=1.225kg/m3，动力黏度μ=1.789×10–5N·s/m2，运动黏度v=1.46×10–5m2/s。若流速超过0.3Ma，气体性质则设为可压缩空气。

2.4 算例验证

为了验证本文仿真方法的合理性，取一段光滑平板进行计算，由于微织构尺度在近壁面的边界层内，因此验证工作是针对近壁区边界层的验证，将摩擦阻力系数理论值与仿真值进行对比（表1），以验证减阻性。

表1 摩擦阻力系数理论值与仿真值对比Table 1 Comparison between theoretical value and simulation value of friction resistance coefficient

取1m 长的平板，由于流速区间较大，流速设置为75m/s，理论上，平板上存在从层流到完全湍流的情况，根据局部雷诺数计算，在该流速下，从0.058m 开始层流就开始向湍流转捩，在0.58m 后处于完全湍流状态。

根据普朗特关于试验的总结，平板湍流边界层摩擦阻力系数遵循以下关系：

其中，Rex由通过平板的位置计算，即距平板前缘的距离。

在FLUENT 中，使用式（14）计算壁面摩擦系数：

其中，τw为平板中点的壁面剪切应力；ρ为流体的密度；ub为平板的平均速度。ρ和ub通过仿真结果后处理，从FLUENT 中获得。

在1m 的平板上取9 个点，均匀间隔0.1m，将这9个点的摩擦阻力系数理论值与仿真值进行对比，具体数据见表1，对比湍流边界层摩擦系数理论值和CFD 计算结果，可以看出，两者的符合程度较高，最大误差在2.5%左右，且在0.6m 开始误差很小，符合0.58m 开始形成完全湍流，因此所选择的CFD 方法满足计算要求的精度。

3 仿真结果及减阻机理研究

3.1 数值模拟计算结果

在物体绕流中，物体形状对物体的阻力影响很大，形状会影响物体表面的压力梯度从而造成压差阻力的改变，而在纵向微织构中，压差阻力不是主要阻力因素，最主要的是摩擦阻力，摩擦阻力与摩擦阻力系数和表面积有关，结构形状主要影响表面积和表面流速。下面选取图10 中的4 种结构进行分析，该形状的灵感主要源于鲨鱼皮表面的盾鳞结构。

图10 微织构沟槽形状Fig.10 Microtexture groove shape

由图11 可知，矩形和三角形的区别在于沟槽内部空间的大小，结果显示三角形的减阻率优于矩形，根据摩擦阻力的计算公式为：

图11 微织构沟槽形状对阻力的影响Fig.11 Influence of microtexture groove shape on drag

其中，Ff为摩擦阻力；Af为表面积。

摩擦阻力与表面积成正比，矩形表面积大于三角形，减阻率小于三角形。由三角形1（w=0.15）和三角形2（w=0.3）进行对比可以发现，宽度增加，摩擦阻力也随之增加，相对减阻率也增大。对比三角形2、梯形以及半圆，三角形的减阻效果比较好。图12 为4 种结构的速度云图，其高度一致，在微织构内部速度都处于低速区，对比矩形和三角形可以发现，在宽度一定的情况下，微织构内部空间并不是越大越好。而三角形和梯形减阻效果差距并不大，半圆形结构边界层相对于其他3 个结构较厚，因此中间高速流区域相对较少，黏滞作用较高。且相对于其他结构来说，半圆形对于气流的影响不大，相当于增加了结构的表面积，阻力系数增加。

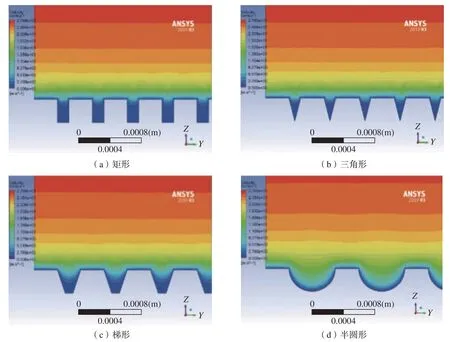
图12 微织构表面速度云图Fig.12 Surface velocity nephogram of microtexture

进一步对摩擦阻力系数进行分析，如图13 所示，在微织构底部，摩擦阻力系数较低，这与该区域流速较低有关，这也验证了摩擦阻力系数受雷诺数影响，由图13（a）可知，在矩形拐角处，摩擦阻力系数变化较大，在沟槽内部拐角，由于气流流速较小，因此摩擦阻力系数也较小，趋向于0。在沟槽表面的拐角，由于处于开放区域，气流流速较高，摩擦阻力系数较高。

从图14 可以看到，微织构表面的压力分布并不均匀，局部区域存在压力差，因此速度并不稳定，容易形成涡流。由图13（b）可以看到，三角形微织构的宽度对表面拐角的摩擦阻力系数有所影响。对于三角形宽度的影响因素将在下文进行详细分析。对比相同宽度和高度的三角形和梯形微织构，摩擦阻力系数分布基本一致，唯一不同点在于沟槽内拐角处。但从总的减阻率来看，沟槽内部拐角并不是越多越好。从结构来看三角形沟槽具有较好的减阻性能，因此对三角形微织构进行微织构的几何特征参数分析。

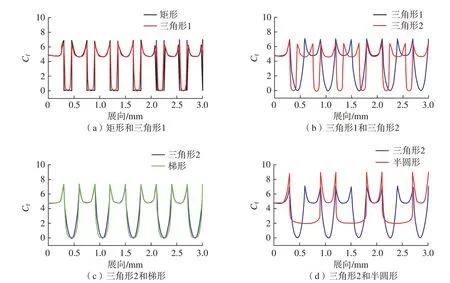
图13 微织构表面摩擦系数分布Fig.13 Friction coefficient distribution on microtexture surface

图14 微织构表面压力云图Fig.14 Surface pressure nephogram of microtexture

图15 为相同宽度、间距（W=S=0.3mm），不同深度的微沟槽对阻力的影响，分析可知：

图15 微织构沟槽深度对阻力的影响Fig.15 Influence of groove depth of microtexture on resistance

（1）在其他参数不变的情况下，随着微织构深度的增加，减阻率的影响呈先增大后减小的趋势，当高度为0.2mm 时具有最佳减阻率，达到2.04%；

（2）通过无量纲参数y+可以发现减阻最高的情况下y+=13.86，宽深比为1.5。

图16 为速度云图，沟槽底部速度较低，随着深度的增加，底部低速区域增加，但是沟槽表面的速度分布没有变化，不会随着深度的增加而增加，只会增加黏性底层的厚度，因此，减阻微织构的深度有一定限制。

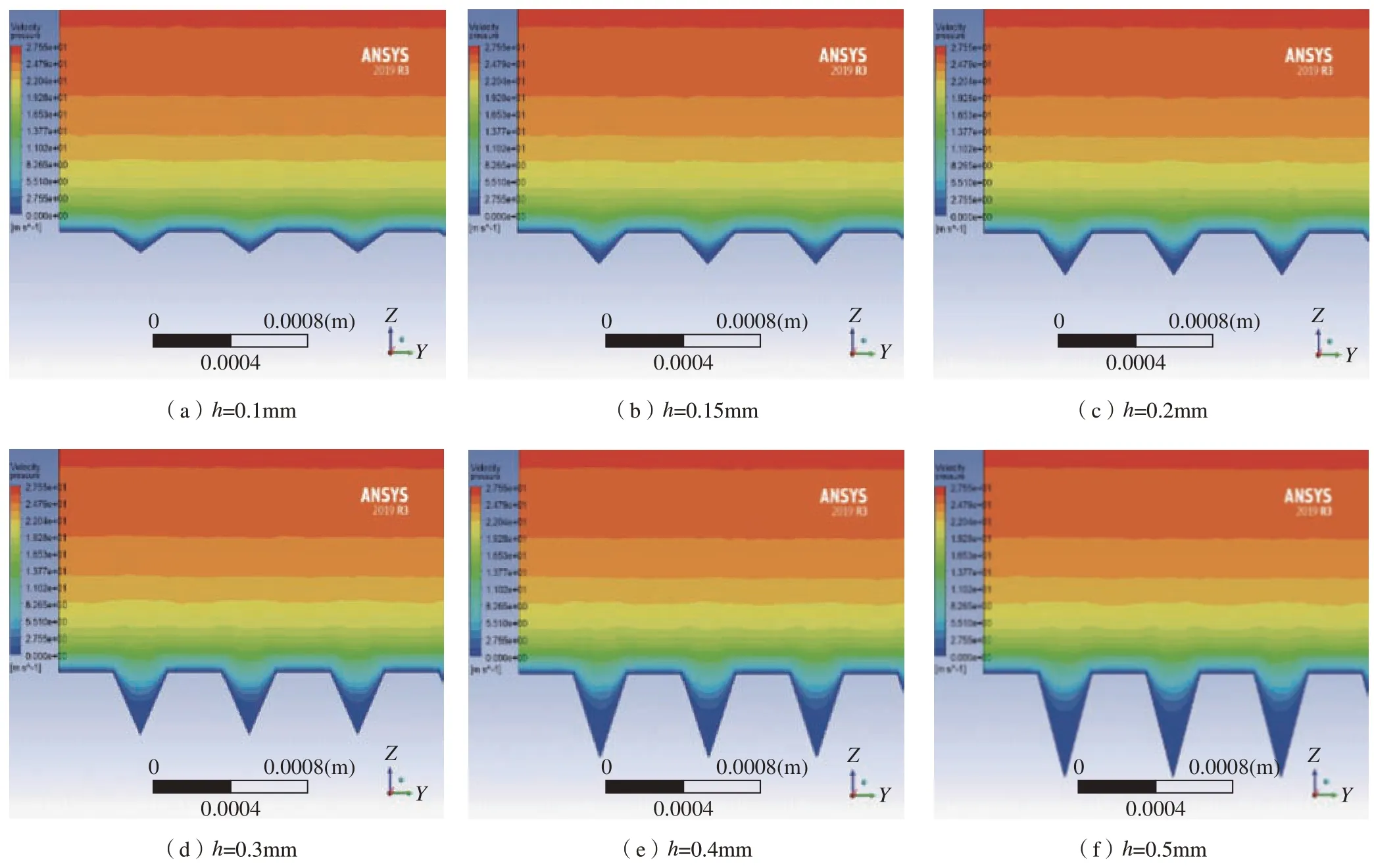
图16 不同深度微织构表面速度云图Fig.16 Surface velocity nephogram of microtexture at different depths

图17 为微织构表面湍动能分布，可以发现，微织构的深度增加可以减小表面湍动能的分布，但同样有深度限制，到一定程度局部湍动能分布就不再变化。当深度增加到0.3mm 时，局部湍动能分布就不再变化。湍动能主要是系统能量耗散的表现，因此可以发现，微织构能够减少系统的能量损失，对于抑制湍流产生具有一定效果。

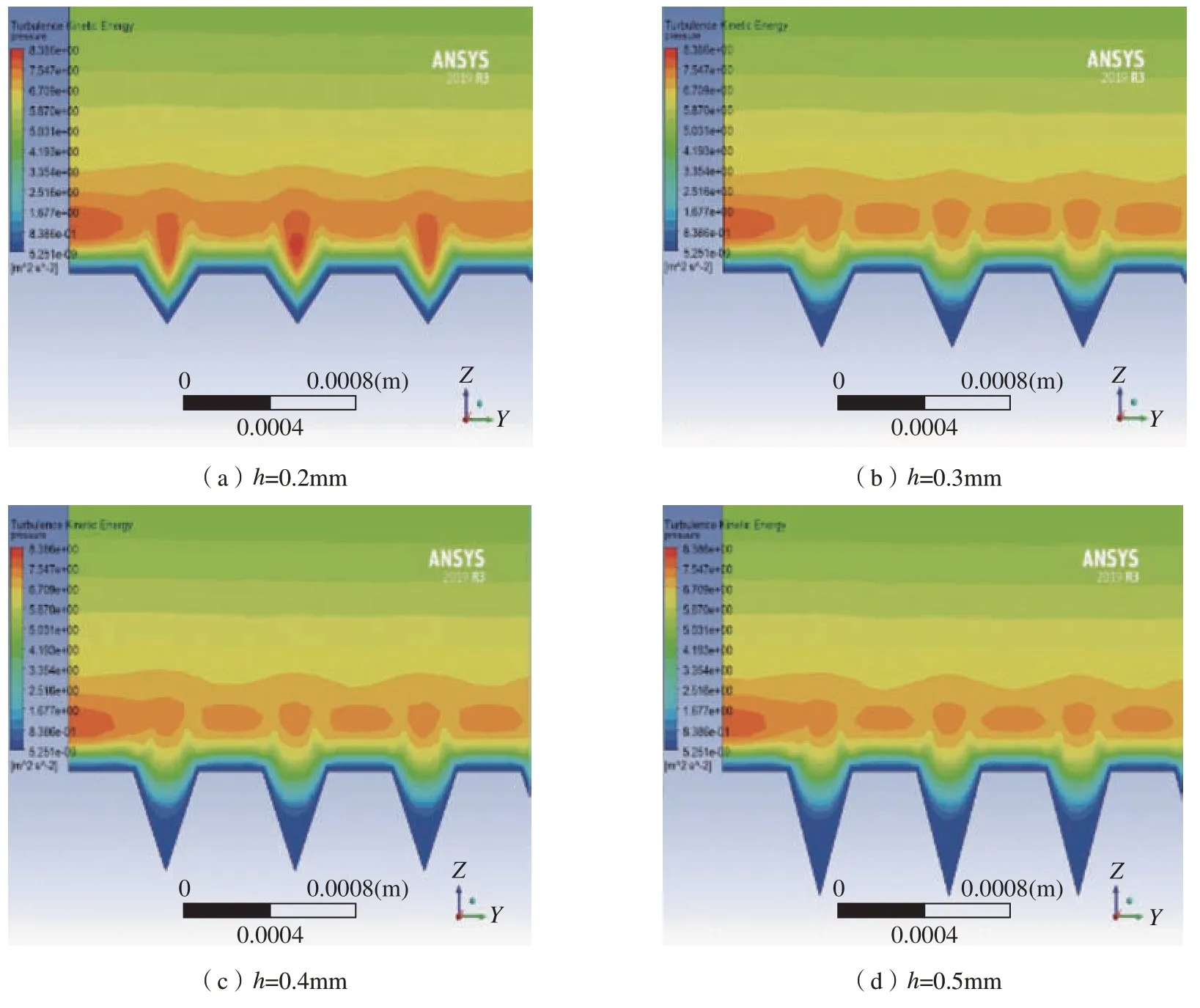
图17 微织构表面湍动能云图Fig.17 Turbulent kinetic energy nephogram of microtexture surface

3.2 减阻机理分析

为进一步研究微织构深度对摩擦阻力的影响，探究微织构的减阻机理，对微织构表面摩擦阻力系数分布进行分析，如图18 所示。微织构深度的增加，在沟槽底部的壁面摩擦系数有所降低，但是在沟槽上表面拐角的壁面摩擦系数会增加，平均摩擦系数随着深度增加而减少，但是表面摩擦阻力与表面积有关，因此深度增加也会造成表面积增加，因此总减阻率呈现先增大后减小的趋势，且随着深度的增加，减阻效果有所下降。

图18 不同深度微织构表面摩擦阻力系数分布Fig.18 Distribution of frictional resistance coefficient on microtexture surface at different depths

从数值模拟结果来看，V 型沟槽表面黏性底层厚度比光滑表面要厚，低流速区的存在，一方面隔离了壁面和高速流体，另一方面，低流速区流动较稳定，降低了边界层的湍动能，减小了近壁区的平均速度梯度，使得表面摩擦阻力减小。

4 各参数对微织构减阻效果的影响规律研究

为了研究V 型微织构设计方法，现对V 型沟槽的几何特征参数和流速进行研究，探究各参数对微织构减阻效果的影响规律。

4.1 宽度参数对减阻率的影响

表2为不同宽度微织构对阻力的影响，对其进行分析可以得到以下2 个结论：

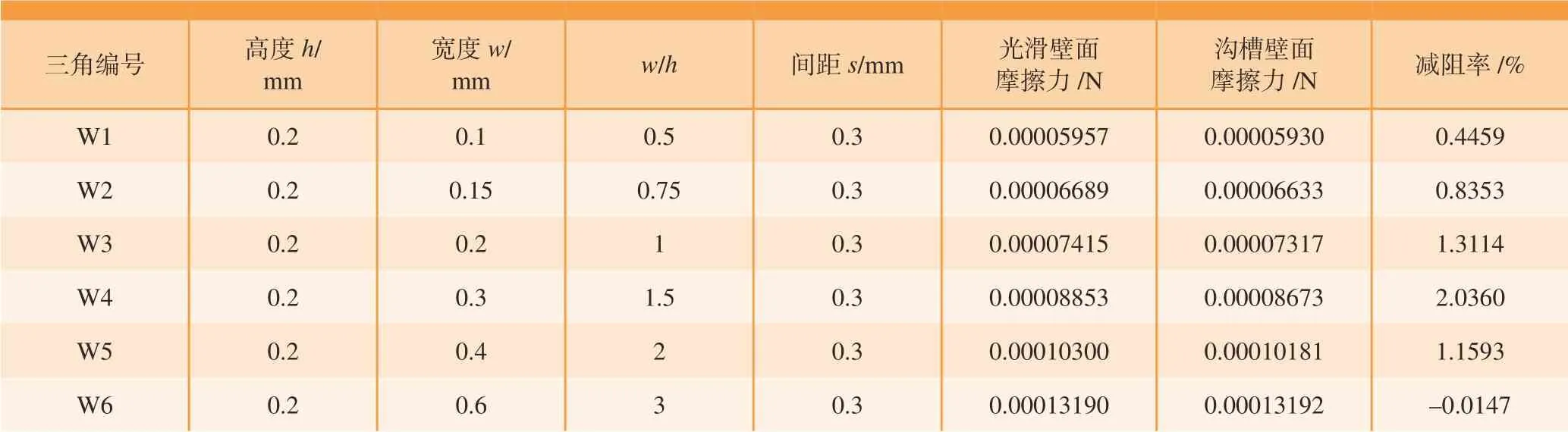
表2 微织构沟槽宽度对阻力的影响Table 2 Influence of groove width of microtexture on resistance

（1）当宽高比<3 时，具有减阻效果，最佳减阻率为2.04%，此时宽高比为1.5 : 1；

（2）随着宽度的增加，物体表面的摩擦阻力递增，与式（15）摩擦阻力系数计算公式相符合。

宽度的增加，增加了微织构表面积，因此摩擦阻力系数增大，总阻力增加。

对不同宽度微织构表面速度云图（图19）进行分析，可以得出，微织构表面的速度梯度分布随着宽度的增加越来越贴近光滑表面。当宽高比大于1.5 时，微织构沟槽内部基本不存在低速区，这种情况下，微织构可以看作是宏观的粗糙表面，粗糙度越大，所受阻力越大，不具有减阻效果。

图19 不同宽度微织构表面速度云图Fig.19 Surface velocity nephogram of microtextures of different widths

对不同宽度微织构表面湍动能云图（图20）进行分析，可以发现，在高度不变的情况下，随着微织构宽度的增加，微织构表面会出现湍动能高亮区域，这代表该区域微织构造成了湍流的形成，对于减阻不利，虽然表现在总阻力上，但是系统的能量损失增加。

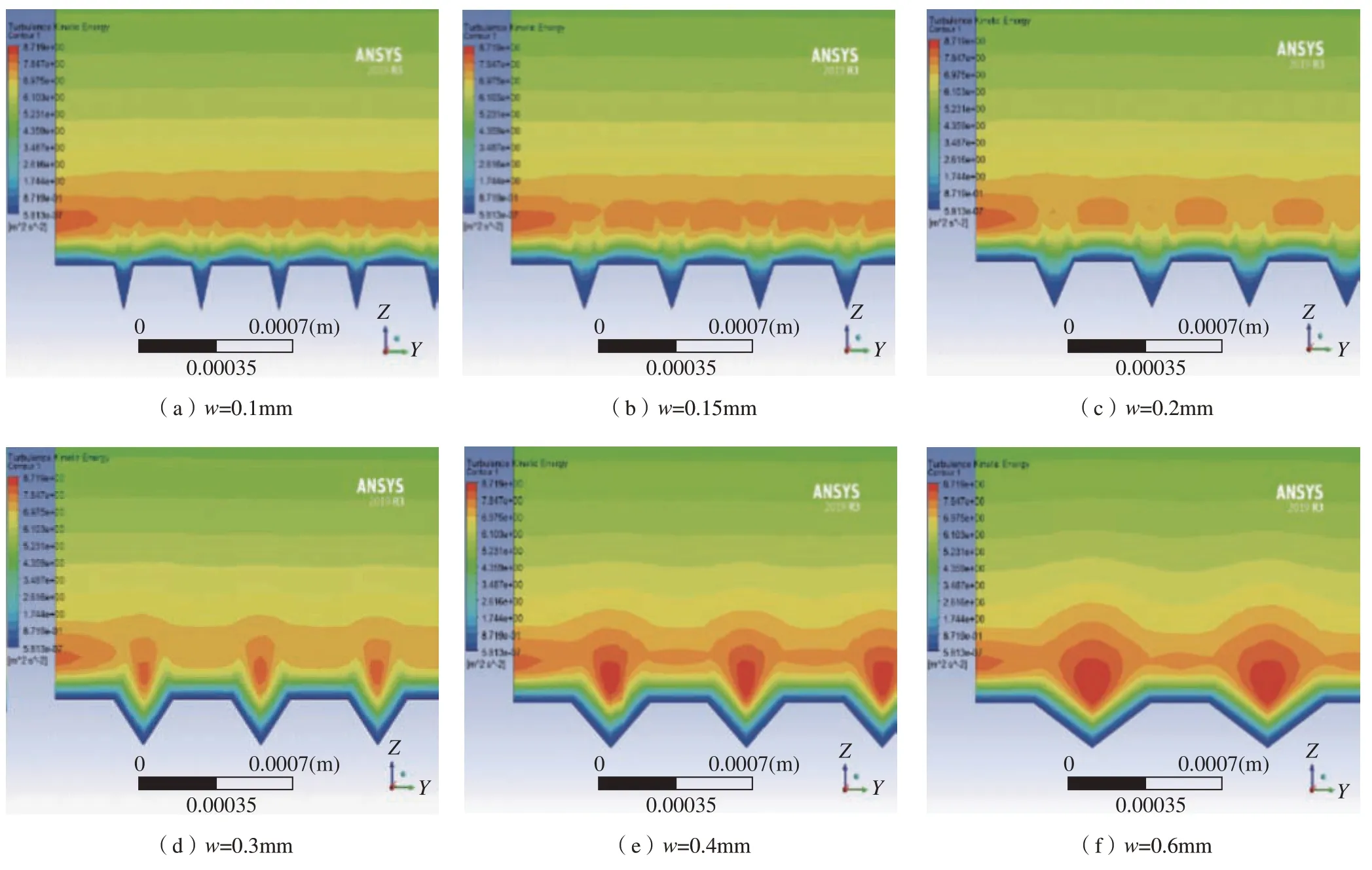
图20 不同宽度微织构表面湍动能云图Fig.20 Turbulent kinetic energy nephogram on microtexture surfaces of different widths

此效应的出现，主要跟三角形微织构的宽高比有关，当宽高比大于1.5 时，就会在沟槽间出现湍流集中区，分析图17 也能反映该结论。因此在设计减阻微织构时，宽高比不能大于1.5。

图21 为不同宽度微织构表面摩擦阻力系数分布，可以发现，沟槽底部最小摩擦阻力系数随着微织构宽度增加而增大，这是因为微织构宽度增加，微织构的微观作用减小，微织构逐渐趋近于宏观的粗糙表面，因此无限制地增加微织构的宽度不会对减阻有明显影响。而微织构沟槽上表面拐点部分的摩擦阻力系数随着宽度的增加先增加，后减少。当开始减小时，说明微织构的微观作用开始减弱，开始向平面化发展。

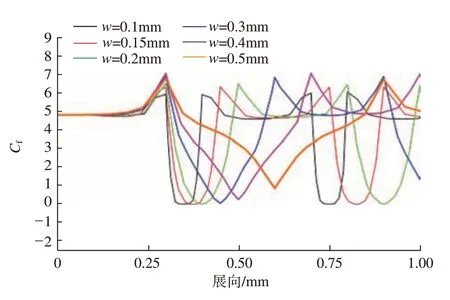
图21 不同宽度微织构表面摩擦阻力系数分布Fig.21 Distribution of frictional resistance coefficient on microtexture surfaces with different widths

4.2 间距参数对减阻率的影响

表3为固定沟槽深度、宽度和数量的情况下，改变沟槽间距的减阻效果表示，可知间距对阻力的影响成反比关系，间距越小，微织构减阻率越高，当间距为0 时最高减阻率达5.5%

图22 为不同间距微织构近壁面的速度分布，可以看到，当微织构的形状、深度、宽度确定时，沟槽内部的速度分布不随间距的变化而变化。因此间距对阻力的影响主要表现在微织构间距那一段区域。而从表3的结果结合式（15）摩擦阻力系数来看，微织构间距越大，表面积越大，导致摩擦系数增大，最终总阻力增加。

图22 不同间距微织构表面速度云图Fig.22 Surface velocity nephogram of microtexture with different spacing

表3 微织构沟槽间距对阻力的影响Table 3 Influence of groove spacing of microtexture on resistance

图23 为不同间距微织构近壁面的湍动能分布，直接结论表面，该宽高比下微织构内部会存在湍动能集中区，但是其强度会随着间距变化，当s/h>0.75 时，沟槽间的湍流区域开始连通起来，当s/h>2 时，间距位置处开始出现局部湍动能集中区，虽然总体仍然呈现减阻效果，但是减阻率降低，且系统能量消耗变大。

图23 不同间距微织构表面湍动能云图Fig.23 Turbulent kinetic energy nephogram on microtexture surfaces with different spacing

图24 为不同间距微织构表面摩擦系数分布，可以看到，微织构内部摩擦系数无差别，差距在间距处，当微织构间距为0 时，该点的摩擦阻力系数最高，但是由于只有一个点，因此总体影响不大，而间距处的摩擦阻力随着间距增大而减小，但减小程度有限，当s/h>2 时摩擦阻力系数已降至最低，扩大间距将对摩擦系数影响不大。虽然摩擦系数降低了，但是表面积增加了，综合来看，摩擦阻力系数增加，摩擦阻力增大。

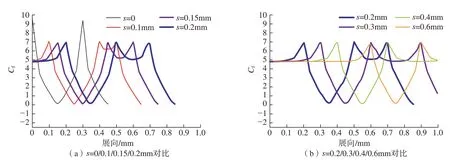
图24 不同间距微织构表面摩擦阻力系数分布Fig.24 Frictional resistance coefficient distribution on microtexture surface with different spacing

4.3 流速对减阻率的影响

表4为流速对于微织构摩擦阻力影响，可以看到，速度变量也是壁面阻力的决定性较大参数，表面摩擦阻力与无量纲高度参数成二次函数关系，如图25 所示。当气体为不可压缩气体时，微织构的减阻效果随着无量纲数增加而降低，但突破0.3Ma 后减阻率随着微织构的高度无量纲数增加而增加。

图25 无量纲高度参数与表面摩擦阻力关系Fig.25 Relationship between height dimensionless number and surface friction resistance

4.4 影响规律总结

（1）对比矩形、三角形、梯形、半圆形，相同深度、宽度、间距、数量情况下，三角形沟槽具有最佳的减阻效果，梯形沟槽其次，半圆形沟槽减阻效果最差。在进行减阻微织构设计时，尽量选择三角形微织构。

（2）在进行减阻微织构设计时，无量纲深度参数保持在14 左右具有最佳减阻效果。由于试验成本以及条件限制，未进行试验验证，但Bechert 等[13]曾对V 形槽平板表面做过风洞试验，结论为当y+=16 时，减阻效果最佳，减阻率为5.1%。试验结果与其试验结果吻合，也可以说明本文仿真手段的有效性。

（3）宽深比必须小于1.5，否则会造成局部高强度湍流区域，虽然总体表现仍然是减阻，但是系统能量损失会增加。

（4）间距对于宽深比为1.5 的沟槽来说，间距越小，其减阻效果越大，因此在布置微织构时，展向连续布置。

（5）速度对于微织构的减阻效果影响较大，速度越大，其边界层越薄，因此相同y+所对应的实际高度y，在高速情况下比低速情况下要小。

5 结论

本文基于边界层理论提出一套减阻微织构的高度和位置设计方法，并通过仿真手段，用离散的方法，对小平面的微织构减阻情况进行了研究，得出以下两点结论：

（1）在其他条件不变的情况下，三角形微织构的减阻效果更佳，在来流速度为25m/s 时，深度0.2mm、宽度0.3mm、间距0 的三角形微织构具有最佳减阻效果，达5.5138%，最佳无量纲参数y+=13.86。

（2）进行减阻微织构设计时，主要的因素为深度，保持在y+=14 左右具有较好的减阻效果。