双扩展卡尔曼滤波法估计锂电池组SOC与SOH
何锋,王文亮,蒋雪生,张小秋
(1.550025 贵州省 贵阳市 贵州大学 机械工程学院;2.550025 贵州省 贵阳市 贵州长江汽车有限公司)
0 引言
锂离子电池具有高能量密度、低自放电率、长循环寿命和环保等特点,在电动汽车电源和储能系统领域得到了广泛的应用。电池管理系统旨在提供监视、诊断和控制功能,以增强电池的运行性能。电池的状态估计是BMS 的基本功能,准确的在线状态估计有助于监测电池的充电状态(SOC)和健康状态(SOH),从而进行合理的充放电,保持电池的高效工作状态和使用寿命[1]。
BMS 主要是通过SOC 值和SOH 值来反映电池的实时状态,SOC 代表的是电池的剩余容量与其满充容量的比值,其准确实时预测关系到电池充放电控制和电动汽车的优化管理,常见的SOC估算方法有安时积分法、开路电压法、神经网络和卡尔曼滤波估算法[2]。安时积分法可以在短时间内实现SOC 的准确估算,但积分过程的累积误差无法消除,导致估计结果不可靠[3];开路电压法需要充放电结束静置一段时间后才能获得较准确的值,不能在线对SOC 进行测量,不适用于电动汽车行驶过程中;神经网络法需要大量的数据进行训练,训练数据和训练方法对估计精度影响较大[4]。基于等效电路模型的卡尔曼滤波算法由于计算复杂度低以及建模精确,已在SOC估计上广泛应用,并取得较好的预测效果。
SOH 代表蓄电池满充容量相对额定容量的百分比,是衡量电池老化程度的度量标准,其主要特征为电池容量的衰退及内阻的增加[5],本文选用内阻作为参数,通过估算内阻来计算得到电池的SOH 值。
国内外现有的估算电池SOH 值的方法主要分为基于耐久性模型的开环方法和基于电池模型的闭环方法[6]。前者主要包括耐久性机理法和耐久性外特性法,此类方法计算复杂且需要进行大量实验,不适用于在线检测;后者包括卡尔曼滤波法、模糊逻辑法和神经网络算法等,这些方法运算简单准确,可以对电池进行实时检测分析,更具有实用价值[7]。卡尔曼滤波法与其他方法相比,需要的数据量较少,相应地计算量也小,估算精度较高,更适用于电动汽车[8]。
本文对磷酸铁锂电池组SOC 与SOH 的精确估计方法进行深入研究,建立2 阶RC 等效电路模型,采用DEKF 算法对电池SOC 和模型参数进行同时估计,通过实时的内阻参数值进而得到相对应的SOH 值,并在DST 工况下验证DEKF算法的估算精度。
1 电池模型
1.1 电池模型建立
卡尔曼滤波器在SOC 与SOH 估计中的成功应用取决于电池的准确模型。许多研究表明,等效电路模型可以成功地用于SOC 与SOH 估计,它可以准确反映电池的物理和化学变化,并且计算成本低,符合BMS 的要求[9]。考虑到电池模型的准确性和计算复杂性,本文采用2 阶RC 等效电路模型,如图1 所示。

图1 2 阶RC 等效电路模型Fig.1 Second-order RC equivalent circuit model
图1 中:R0——欧姆内阻;Cc,Rc——电化学极化电容和电阻;Cd,Rd——浓度极化电容和电阻;Uocv,Uout——开路电压和端电压;I——电池工作电流。
根据模型结构,可推导出模型方程如下:

1.2 电池模型参数辨识
实验采用24 A·h/3.3 V 磷酸铁锂电池(16 个串联组成的电池组)为研究对象,使用IGBT-100V/200A-2 动力电池检测系统设备按12A电流对电池进行间歇恒流脉冲放电实验,根据实验数据对电池模型进行参数辨识。放电间歇周期为62 min,其中,放电12 min,静置50 min,使得开路电压恢复稳定值并记录下来,此时,开路电压约等于电池电动势。每次循环 SOC 减少10%,测试时间为13 h。间歇恒流脉冲工况如图2所示。

图2 恒流放电电流图Fig.2 Constant current discharge current diagram
图3为恒流放电实验中电池端电压的部分曲线。由图3可以看出,当电池开始放电和结束放电的瞬间,电压会有一个阶跃性突变,AB 段和CD 段的电压突变是由电池欧姆内阻引起的,而BC 段和DE 段电压缓慢变化则是由电池极化效应引起的。脉冲放电后E 点电压值要小于A 点的电压值,是因为电压随着电池的SOC 的变化而变化引起的。

图3 恒流放电电压波形图Fig.3 Constant current discharge voltage waveform
1.2.1 电池欧姆内阻辨识
由于电压的突变是由电池欧姆内阻引起的,如图3 所示,记AB 段放电开始电压差为ΔU1,CD 段放电结束电压差为ΔU2,通过这两段电压的变化值来求欧姆内阻值,如式2 所示 :
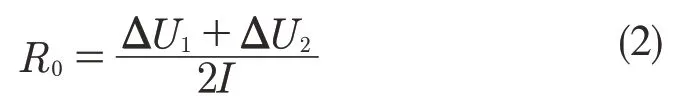
计算可得R0=0.0547 4 Ω。
1.2.2 电池极化电阻和极化电容辨识
图3 中,BC 段为零状态响应,DE 段为零输入响应。如图1 电路模型所示,用2 个RC 并联回路来模拟电压零输入响应,则DE 段端电压如式(3)所示。

式中:Δt——采样时间,利用MATLAB 的Curve Fitting 工具箱进行函数拟合,最终得到电池模型参数为Cc=9 073.18 F,Rc=0.038 64 Ω,Cd=20 487.16F,Rd=0.032 96 Ω。
1.3 OCV-SOC 曲线实验标定
通过进行间歇恒流脉冲放电实验,记录电池SOC 逐渐递减所对应的开路电压数据,采用六阶多项式对数据进行拟合,得到拟合式(4),拟合结果如图4 所示。


图4 OCV-SOC 曲线拟合图Fig.4 OCV-SOC curve fitting diagram
2 SOC 与SOH 估计
2.1 双扩展卡尔曼滤波法估计SOC 和电池模型参数
为实现电池SOC 和电池模型参数的同时在线估计,设计了2 个并行运行的扩展卡尔曼滤波器,第1 个滤波器用于SOC 估计,另一个用于预测电池模型参数。电池SOC 表达式如式(5):

式中:库伦效率γ=1;SOC0——初始值;采样时间t=1 s;Cn——电池实际容量。
对式(1)进行离散化并联合式(5),得到状态方程:

锂电池的动态变化可通过式(6)和式(7)表示,状态向量xi=[SOCi,U1,i,U2,i]T,时间常数τa=RcCc和τb=RdCd,开路电压Uocv可通过和SOC的关系拟合得出。用于估算SOC 的扩展卡尔曼滤波器,根据式(6)和式(7)分别得到电池SOC 的状态和观测方程。

式中:输出yi=Uout,i;控制变量ui=Ii;过程噪声~N(0,Qx);观测噪声~ N(0,Rx)。
完成SOC 估算后,SOC 便成已知输入量,另一个扩展卡尔曼滤波能够实现对电池模型参数θ的估计,在式(8)和式(9)基础上,得到θ的状态与观测方程。

式中:模型参数θi=[R0,Rc,Cc,Rd,Cd]T;过程噪声~N(0,Qθ);观测噪声~N(0,Rθ)。
双扩展卡尔曼滤波算法(DEKF)步骤如下:
步骤1:初始化X0,,Px;,Pθ。
步骤2:模型参数时间更新

步骤3:状态时间更新

步骤4:状态观测预测

步骤5:协方差匹配

步骤6:模型参数观测预测

通过式(12)—式(16)不断进行时间状态更新和状态观测更新,即可估算出实时的模型参数和状态变量SOC。
2.2 SOH 估计
内阻的变化是衡量电池SOH一个关键指标,根据DEKF 算法估计出的电池模型参数,本文取电池内阻作为SOH 的表征量,欧姆内阻和SOH的函数关系如式(17)和式(18)定义。
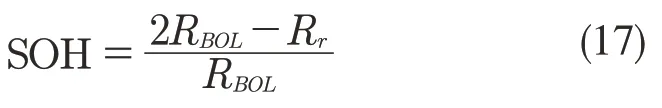

式中:RBOL——新电池内阻;REOL——电池寿命终止时内阻;Rr——电池当前真实内阻。
3 实验验证与分析
为验证DEKF 算法的估算精度,实验选取DST 工况进行验证,单个DST 工况循环测试的时间为 360 s。电流的工步设置如表1 所示,电流曲线如图5 所示。正电流表示充电过程,负电流表示放电过程。

表1 单个DST 循环测试工步电流Tab.1 Single DST cycle test step current

图5 单个DST 工况电流图Fig.5 Single DST working condition current diagram
图6 是在DST 工况下进行的SOC 对比,EKF 算法和DEKF 算法的SOC 初值设为0.7。从图6 可以看出,两种算法都能追踪真实SOC,并且DEKF 算法最快到达收敛阶段且适应性更好。EKF 算法和DEKF 算法的MRE 分别为4.59%、1.53%,它们的RMSE 则分别为5.12%,2.23%。体现了DEKF 算法在SOC 初始值不准确的条件下估计精度的优势。

图6 DST 工况SOC 估计结果Fig.6 SOC estimation results under DST conditions
图7 是在DST 工况下采用DEKF 算法进行的R0估计和SOH 估计,通过采集到的实验数据每隔10%SOC 计算得到真实电池内阻,由R0估计结果得知,电池在开始放电和放电结束时,内阻变化较大,而在放电过程中能较好地收敛于真实内阻值,说明算法对 R0可以完成较好的估算。根据估算得出的的内阻值,采用式(17)可以估计出电池的实时SOH 值,由SOH 估计结果得知,电池处于健康状态,验证了算法准确的预测性能。

图7 DST 工况R0 和SOH 估计结果Fig.7 R0 and SOH estimation results for DST conditions
4 结论
本文在2 阶RC 等效电路模型的基础上建立DEKF 算法。该算法可以同时估计锂电池组的SOC 和电池模型参数,并通过对电池内阻的估计转换为对SOH 的估计。在DST 工况下验证分析表明,在SOC 初始值存在误差的实验条件下,DEKF算法估计结果收敛更快,精度更高,估计出的内阻值能实时反映SOH 的变化状态,对实现电动汽车电池状态的实时检测和估算具有重要意义。

