商用车膜式空气弹簧刚度特性研究

黄华，何锋，杨洪江，王铭昭

（1.550025 贵州省 贵阳市 贵州大学 机械工程学院；2.550025 贵州省 贵阳市 贵州宏洋橡胶制品有限公司）

0 引言

橡胶空气弹簧具有静态和动态刚度及阻尼非线性调节功能，已广泛应用于车辆、机车、高铁等交通领域。针对车辆行驶过程中遇到外界干扰因素引起的相关振动所导致其舒适性差的问题，研究橡胶空气弹簧的刚度特性具有重要的意义。

国外研究学者提出了一系列空气弹簧刚度计算的定性分析方法[1-5]，而对橡胶空气弹簧刚度进行准确预估需要有限元法结合相关试验进行定量分析。此外，国内一些学者采用有限元解析空气弹簧静态刚度特性[6-8]，并从舒适性、安全性[9]和整车匹配的角度[10]对空气弹簧进行非线性特性分析，提出了空气弹簧的刚度工作曲线方程，并对其有效性进行了验证[11]。上述研究或运用理论计算，或理论结合仿真，而空气弹簧的实际工作过程是一个多变状态。

本文针对影响空气弹簧刚度特性的气囊有效承载面积、气囊直径和初始压力参数，并以理论为基础开展空气弹簧性能研究，搭建商用车空气弹簧非线性模型，分析其刚度特性并进行试验验证。

1 膜式空气弹簧结构及特点

橡胶空气弹簧如图1 所示的简图结构包括：橡胶气囊、上下盖板及缓冲块等部件。该结构特点是通过压缩空气单元内的气体实现弹簧功能。

图1 橡胶膜式空气弹簧基本结构简图Fig.1 Basic structure of rolling lobe air spring

空气弹簧的刚度随着有效支承面的增加而增加，并且它所承受的载荷越大，反之亦然。因此，橡胶空气弹簧气囊具有理想的非线性特性。

2 空气弹簧刚度理论

将该模型单元中的气体设定为理想气体，根据空气弹簧受力f 可用空气弹簧气囊内部压力和空气弹簧有效承载面积来表示：

式中：Pb——标准大气压；Pa——任意位置下该结构气囊里气体的压力；Aeff——该结构的负载有效面积。

橡胶空气弹簧内部气体是一个多变的过程，主要取决于气体多变指数γ，其内部气体与容积的变化的理想气体状态方程为

式中：P0——初始状态下橡胶空气弹簧气囊内气体的压力；V0——初始状态下橡胶空气弹簧的容积；Va——橡胶空气弹簧在任意位置的体积；γ——理想气体多变指数。

将式（2）变形代入式（1）中整理得出橡胶空气弹簧的载荷f 为

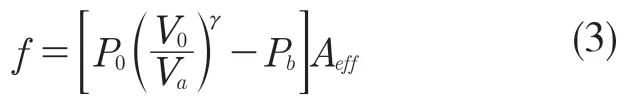
橡胶空气弹簧刚度可以用空气弹簧在一个加载周期载荷变化量与之相对应的位移变化量之比表示，即是橡胶空气弹簧所承受的力对其垂向位移 x 的微分即是刚度：

气体变化过程的流动速率决定了气体多变指数的值，绝热过程：γ=1.4；恒温过程：γ=1.0。根据车辆的行驶状态，确定多变指数，进而决定了空气弹簧所处的刚度为静态刚度或者动态刚度范围。

取γ=1，Va≈V0，因本文研究橡胶空气弹簧静特性问题，则简化后的橡胶空气弹簧刚度公式为：

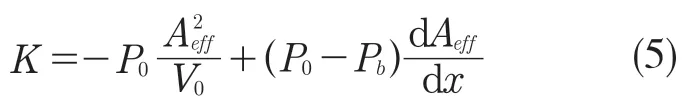
分析式（5）可得，橡胶空气弹簧的刚度与初始压力、空气弹簧有效受载面积、不断变化的有效受载面积变化率及空气弹簧容积有关。

3 空气弹簧模型

3.1 构建空气弹簧模型

采用UG 构建空气弹簧模型，经过HyperMesh 进行空气弹簧的模型预处理及网格划分，这样可提高划分网格质量，同时减少后期分析因网格而产生的错误，最后在ABAQUS 工具中设置相关参数，如图2所示为最终的有限元模型。

图2 空气弹簧有限元分析模型Fig.2 Finite element analysis model of air spring

在软件ABAQUS 中导入空气弹簧分析文件，设置相关参数，橡胶气囊选择超弹性能的Mooney—Rivlin 模型进行分析，根据实际情况进行的单轴试验、双轴试验、平面试验和体积试验获得相关橡胶材料参数和上下盖板材料属性，如表1 所示。

表1 橡胶和上下盖板材料参数Tab.1 Material parameters of rubber and upper and lower cover plates

同时,设置Rebar 帘线的相关弹性参数。加强筋Rebar 模型图如图3 所示。最后,对应指派相应的材料属性。

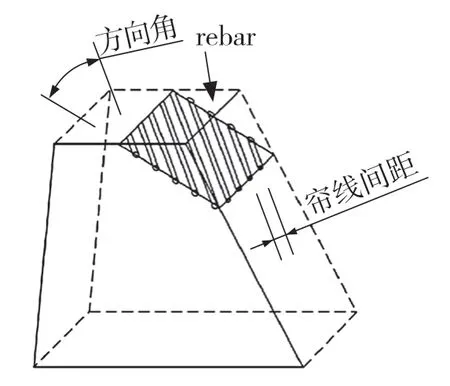
图3 帘线层rebar 模型图Fig.3 Rebar model diagram of cord layer

3.2 空气弹簧边界条件和约束

将上下盖板设置为刚体，用tie 分别模拟与橡胶气囊囊体的接触，橡胶气囊为主动接触面，盖板为从动接触面，同时设定为无滑移接触。采用fluid cavity 分析气囊内的气体单元，在橡胶气囊体中嵌入帘线平面，模拟囊体与帘线层的接触。

上盖板在Y 方向标定空气弹簧位移行程为±80 mm，其余方向完全约束，下盖板完全约束，在气囊腔内建立压力加载点，同时创建分析步step1，step2 及定义输出场，进行仿真分析。

4 空气弹簧刚度特性分析

针对前面内容对空气弹簧刚度的推导，在保证空气弹簧帘线间距、帘线角度及帘线层数及其材料相同的前提下，文中讨论了不同初始压力对影响空气弹簧刚度的影响。

将0.3，0.4，0.5 MPa 的初始压力分别充入橡胶气囊内，阐述该模型的载荷-位移曲线性能，如图4 所示，前提条件是在不改变其帘线间距和工作帘线层数等其他参数的情况下进行。

图4 不同初始压力的空气弹簧载荷—位移曲线图Fig.4 Load-displacement curve of air spring with different initial pressure

分析图4 可知，在该结构的压力承载能力区间，其工作负荷能力与其工作压力成非线性正相关变化。在空气弹簧实际工作条件下，如果压强一定，空气弹簧在一定工作高度范围内承受的载荷变化趋于平稳。

橡胶空气弹簧的刚度为载荷—位移曲线上任意一点的斜率，表达式为

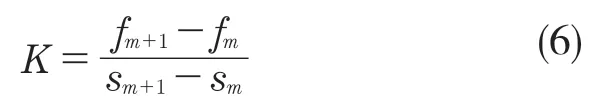
式中：K——刚度；f ——载荷；s ——位移。根据图4和式（6）剖析，获得如图5所示的变化曲线，即为该结构在相应工作压力的刚度数值。

图5 不同初始压力的空气弹簧刚度—位移曲线图Fig.5 Stiffness-displacement curves of air springs with different initial pressures

该模型在进行压缩和拉伸试验时，其刚度曲线呈现“U”型变化，在最大压缩处（-80 mm）达到最大值分别为115.0，161.5，180.0 N/mm，对应最大拉伸处的刚度值比压缩处的刚度略小，而在空气弹簧标准高度下的刚度几乎为零。意味着空气弹簧具有非常好的工作特性，为匹配车辆的悬架系统提供了适宜的刚度选择区间。

5 试验验证

为保证空气弹簧在不同初始压力下的承载能力准确性，对橡胶空气弹簧进行拉伸试验验证，如图6 所示。对影响空气弹簧刚度的有效面积参数进行试验分析，并进行试验数据拟合，得到如图7 所示的曲线图。

图6 橡胶空气弹簧试验测试平台Fig.6 Rubber air spring test platform

图7 空气弹簧有效面积—压力曲线图Fig.7 Air spring effective area-pressure curve

由图7 可得，当空气弹簧最初施加0.1 MPa的压力时，其有效面积出现下降趋势，由于空气弹簧的正常工作压力在0.3～0.8 MPa 之间，在0.3 MPa 之后，商用车空气弹簧有效面积与其工作压力成正相关关系，且呈现非线性的上升状态，即空气弹簧刚度随之增大。

对该结构的体积变化对其刚度特性影响进行分析，结果如图8 所示。

图8 空气弹簧直径—压力曲线图Fig.8 Air spring diameter-pressure curve

由图8 可知，主要决定空气弹簧容积参数的是其直径。同理，根据式（5）与图8 可得，该结构的工作直径随压力的变大进一步增大，即体积增加，由该模型承载能力增大，是其有效承载面积的变化结果。

从图9 分析可知，不同压力下的仿真数据与试验数据性能曲线比较吻合，通过计算得仿真拟合误差，如表2 所示。分析表中数据可知拟合误差较小，反映仿真分析曲线能够较好地预测实际橡胶空气弹簧的特性曲线，然后对有限元模型的精度进行了验证。

图9 空气弹簧试验性能曲线对比Fig.9 Comparison of air spring test performance curves

表2 仿真拟合误差Tab.2 Simulation fitting errors

6 结语

本文基于商用车用橡胶膜式空气弹簧，利用ABAQUS 对空气弹簧进行参数仿真，并分析其特性试验，总结出两条结论：

（1）通过对膜式空气弹簧进行仿真分析及其计算表明，在不同初始压力下，该结构的承载能力同工作压力增大而逐渐变大。

（2）通过对该模型的试验测试结果与仿真结果进行对比分析，同时验证并完善仿真模型，提高其准确性，给该模型后续的基础分析研究提供参考。