基于有限元模型的永磁同步电机定子模态分析

周宇，郭浩

（200093 上海市 上海理工大学 机械工程学院）

0 引言

电动汽车的使用越来越广泛，伴随着电动汽车的普及，对电动汽车的核心部件的需求也逐渐增大，因此，对它们的要求也越来越高。驱动电机是电动汽车的核心部件，对它的研究与开发受到了国内外工程师们的高度重视。永磁同步电动机（PMSM）具备了功率密度高、效率高以及体积小等优点，因此已成为电动汽车的首选驱动电机[1]。随着汽车轻量化的进程，在追求驱动电机轻量化的同时，也会伴随出现各种各样的问题。电机的结构设计以质量轻、体积小为主要目标，但是其刚度相对较差，工作时容易产生较大的振动和噪声问题，从而影响驾驶员的行驶以及电机的性能和可靠性。转子振动及其控制是电力工业机械面临的主要挑战之一。永磁同步电动机的振动和噪声主要来源于机械、空气动力和电磁；机械噪声主要是由轴承等机械因素引起的，一般频率相对较低，其源识别技术已趋于成熟；空气动力噪声主要来自冷却风扇，但电动汽车中的永磁同步电动机通常没有带风冷或水冷的风扇，因此，气动噪声可以忽略不计；电磁噪声主要是由作用在定子齿面和永磁体表面的法向电磁力引起的，这与电机的电磁参数和控制策略密切相关；定子的电磁噪声是大多数永磁同步电机的主要组成部分，因此，对定子的电磁振动与噪声的研究对于降低驱动电机的噪声具有重要意义。设计电动汽车永磁同步电动机时，需着重研究电机的振动特性以及对电机安排合理的振动测试。模态分析是结构动力分析和振动分析的基础。电机模态分析主要有3 种方法：分析法、有限元法和试验法[2]。其中，解析法仅适用于结构简单、易于分析的电机；有限元法可用于不规则电机结构的模态计算，且精度高，应用更为广泛，但该方法的计算精度取决于模型的材料属性参数和几何参数的精度。用模态试验方法得到的模态参数比较准确，但由于需要在电机表面放置大量的传感器，需要更多的测试通道，因此成本较高。国内外许多学者用有限元法和实验模态法对工业电机的模态和振动特性进行了大量的研究[3-8]，但对电机的模态和振动特性的研究文献相对较少[9-11]。

本文对一台额定功率为42 kW 的电动汽车驱动电机进行了模态分析，通过仿真得到了电机的固有频率和振型。此外，将用振动试验台对样机进行模态试验验证，同时，根据电机定子的模态参数，对定子结构进行了改进设计。

1 永磁同步电机定子模态分析

本文所研究的电动汽车驱动电机是一种强制水冷式永磁同步电动机，主要由前端盖、机壳、铜线定子转子和后端盖组成。有限元模态仿真计算的解域是电机的核心部件之一定子。

利用UG NX10.0 软件建立电机定子几何模型，如图1 所示，其几何参数见表1。由于端部绕组形状复杂，对网格的数量和质量影响较大，但对模型整体刚度的影响较小，因此，模态分析中没有建立端部绕组的实际模型，而是将相应的绕组质量转化为定子槽。

图1 定子及其绕组的三维模型Fig.1 Three dimensional model of stator and its winding

表1 定子和绕组几何参数的建模Tab.1 Modeling of stator and winding geometric parameters

定子和绕组组件中包含的材料类型通常为硅钢、铜和树脂。模型与Solid186 单元类型啮合。单元总数为834 178，节点总数为3 408 452。模型的总自由度为10 230 000，有限元模型如图2所示。

图2 定子的有限元模型Fig.2 Finite element model of stator

由于电机在自由状态下进行模态计算，因此不施加任何约束。利用有限元仿真软件WorkBench 计算了永磁同步电机定子的固有频率和模态。从自由状态下电机定子的模态计算中提取前7 阶固有频率及其对应的模态。仿真结果如表2 和图3 所示。本文研究的永磁同步电动机极数为4 对极，最大转速为10 000 r/min，即最大工作频率比电动机的第一固有频率630.7 Hz 高1 333.3 Hz，因此，根据仿真结果，电动机结构可能发生共振。

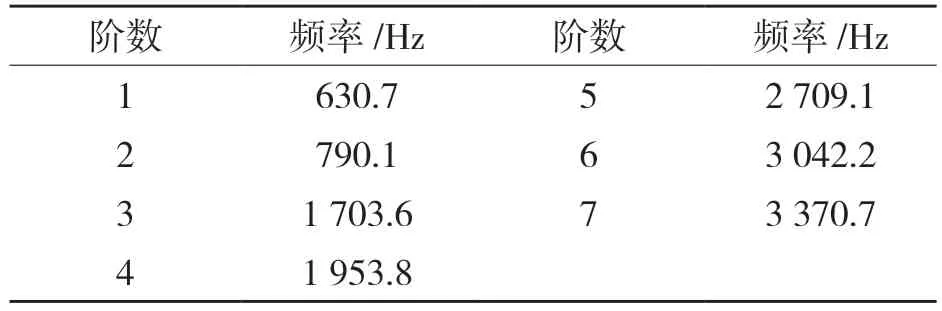
表2 电机定子模态参数仿真结果Tab.2 Simulation results of modal parameters of motor stator

图3 定子模态有限元仿真结果Fig.3 .Finite element simulation results of stator mode

2 电机定子模态试验分析

为了验证电机有限元模态计算的可靠性，对电机定子进行了模态试验分析。

电机定子质量为16.2 kg，采用DASP306 智能信号测试分析系统对振动特性进行测试。该系统包括数字采集仪、数据线、便携式计算机和三向加速度传感器等，并结合DASP 软件进行数据分析。传感器类型为BZ1102，灵敏度为0.55 PC/ms-2。该传感器的频率响应为1～25 000 Hz，质量为5 g，锤式力传感器为BZ1202，灵敏度为4.22 PC/N。模态试验装置和测量仪器如图4 和图5 所示。

图4 对电机定子进行模态试验Fig.4 Modal test of motor stator

图5 DASP 测量系统Fig.5 DASP measurement system

为了准确提取定子的模态参数，获得较好的模态动画效果，根据定子的形状和结构，在定子上布置了64 个测点，布置在定子外缸表面，沿母线分成4 条等距线。每条线沿定子铁心圆周有16 个点。以定子轴线的轴线方向为轴，定子铁心柱面的法向为径向，法向与轴向的正交为切向，建立定子坐标系。由于采集仪器的通道数、传感器和采样频率的限制，将64 个测量点分为3 组，第1 组和第2 组分别有22 个测点，第3 组有20个测点。定子测点模型图如图6 所示。

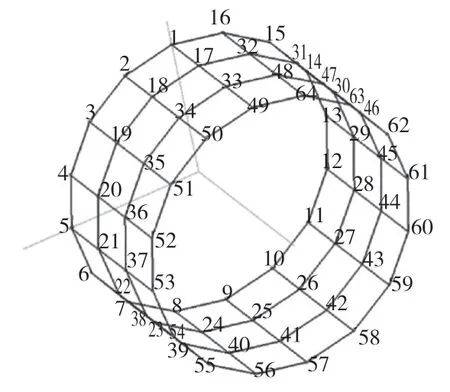
图6 定子测点Fig.6 Stator measuring points

3 结果与讨论

根据相干性分析结果，确定了冲击波在径向、轴向和切向3 个方向上的激发点。模态试验要求相干系数大于0.90。取ρ（径向）激发点为第10测点，取Z（轴向）激发点为第10 测点，取φ（切向）为第9 测点。由于定子外表面光滑，无突起，切向锤击困难。必须在第9 个测量点安装辅助液压锤轴承。辅助轴承由钢制成，其质量为38.2 g。滤波分析频率设为6 666.67 Hz，采样频率设为17.067 kHz。将固有频率仿真数据与实验数据进行比较，可以看出模拟与试验数据的误差在-0.33%～4.98%之间。实验结果与仿真结果基本一致，证明了所建立的定子有限元模态仿真模型的实用性。此外,由表3 可知，电机的径向电磁激振力可激发2 阶、4 阶和6 阶模态频率。

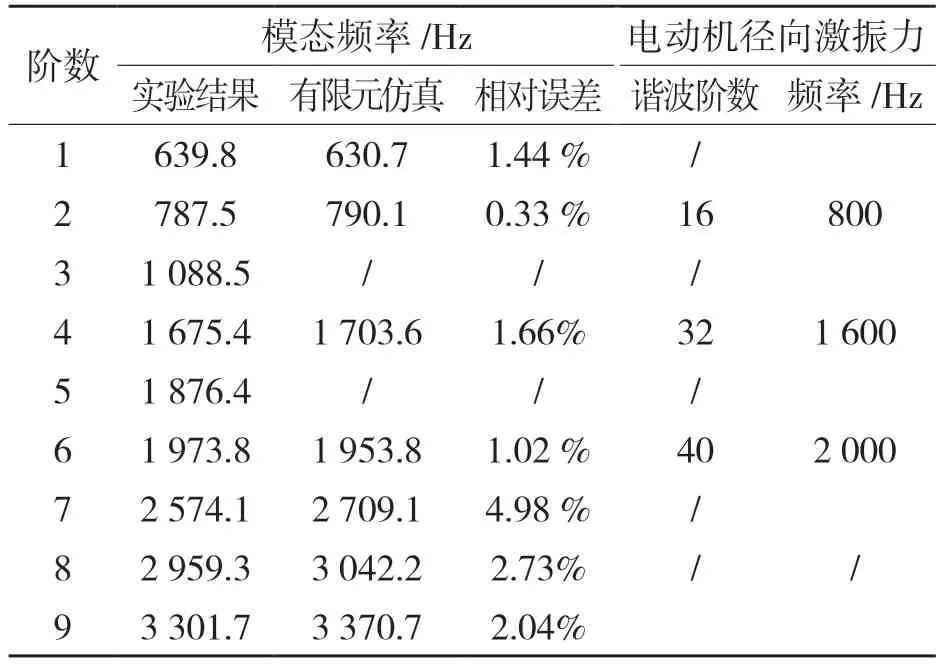
表3 定子模态参数有限元仿真与实验结果的比较Tab.3 Comparison between finite element simulation and experimental results of stator modal parameters

为了分析车辆用永磁同步电动机的振动特性，对额定功率为42 kW 的电机定子进行了模态分析。主要结论如下：

（1）对电机定子进行了有限元模态分析，计算出电机定子的2 阶、4 阶和6 阶固有频率分别为790.0，1 671.8，1 986.10 Hz。这些模态频率可由电动机的径向电磁激振力激发。通过对电机定子振动模态的分析，判断定子径向刚度较弱。本文建议适当加强定子的径向刚度。

（2）试验测得的电机定子固有频率与仿真计算值的误差分别为-1.44%和4.98%，验证了仿真的准确性。

4 结论

为了分析电动汽车永磁同步电机定子的振动特性，本文首先对额定功率为42 kW 的电机定子进行了模态分析，为了验证电机有限元模态计算的可靠性，对电机定子进行了模态试验分析。主要结论如下：

（1）对电机定子进行了有限元模态分析，计算出电机定子的2 阶、4 阶和6 阶固有频率分别为790.1，1 703.6，1 953.8 Hz。这些模态频率可由电动机的径向电磁激振力激发。通过对电机定子振动模态的分析，判断定子径向刚度较弱。建议适当加强定子的径向刚度。

（2）试验测得的电机定子固有频率与仿真计算值的误差分别为-1.44%和4.98%，验证了仿真的准确性，说明了对电机进行仿真分析途径的可行性。