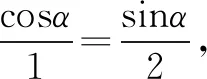高中数学辩证思维赏析
李莉莉
(四川师范大学附属中学 610066)
数学与哲学是两门独立的学科,同时又是两门联系紧密的学科.正如数学家Demollins所指出的那样:“没有数学,我们无法看透哲学的深度;没有哲学,人们也无法看透数学的深度;若没有二者,人们就什么也看不透.”恩格斯也指出:“数学中的转折点是笛卡儿的变数.有了变数,运动进入了数学,有了变数,辩证法进入了数学,……”.在《普通高中数学课程标准(2017年版)》修订的基本原则中也要求:“坚持正确的政治方向……充分体现马克思主义的指导地位和基本立场……”.课程标准全书的表述中也渗透了辩证法的很多观点,本文将结合高中数学代数课程教学现状中的相关教学内容,对基于辩证思维的高中数学题型讲解策略展开具体的分析和探究.
一、辩证思维中对立统一的规律
高中代数中蕴含了丰富的对立统一思想,从不同的角度看问题,有不同的解法,会让我们对问题的研究更深入.
例1(2014年全国新课标Ⅱ文科21第Ⅱ问)已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2.
(1)求a;(a=1,解略)
(2)证明:当k<1时,曲线y=f(x)与直线y=kx-2只有一个交点.
赏析一(2) (虚设零点法)原命题等价于函数g(x)=f(x)-kx+2=x3-3x2+(1-k)x+4与x轴只有一个交点,问题转为研究函数g(x)的图像性质.由g′(x)=3x2-6x+1-k,
①当Δ=36-12(1-k)=24+12k≤0,即k≤-2时,g(x)在R上单调递增,因为g(-1)=k-1<0,g(0)=4>0,所以存在唯一x0∈(-1,0),使得g(x0)=0,得证.
②当Δ>0,即-2 由单调性,易知g(x)的图象与x轴只有一个交点,只需要证得g(x2)>0即可. 所以,当-2 综上可知,命题得证. 此方法从整体出发,直译条件,思维简单,在计算中使用了“反代消参”的方法,用零点x2来表示参数k,降低了计算的难度. 赏析二(2) (放缩法)从局部入手,考虑到1-k>0,可以采用放缩法去掉参数,变动为静,简化问题. (1)当x≤0时,g′(x)=3x2-6x+1-k>0,g(x)单调递增,又因为g(-1)=k-1<0,g(0)=4,所以g(x)=0在(-∞,0]有唯一实根. (2)当x>0时,令h(x)=x3-3x2+4,则g(x)=h(x)+(1-k)x>h(x).h′(x)=3x2-6x=3x(x-2),h(x)在(0,2)单调递减,在(2,+∞)单调递增,所以g(x)>h(x)≥h(2)=0,所以g(x)=0在(0,+∞)没有实根,问题得证. 否定之否定规律表明事物自身发展的整个过程是由肯定、否定和否定之否定诸环节构成的,揭示了事物发展的全过程和总趋势.事物都有肯定方面和否定方面,当肯定方面居于主导地位时,事物保持现有的性质、特征和倾向,当事物内部的否定方面战胜肯定方面时,旧事物就需要转化为新事物.高中数学解题思想方法中的补集思想,反证法就是否定之否定规律的具体运用. 我们在高中数学课堂上解决一类关于函数、方程、不等式的双变量(或多变量)的问题时,常常会用到“变更主元”的思想.实时转变观察和思考问题的角度,合理选择恰当的“主元”来解决问题可能更迅速. 例3(2006年四川卷文科21题)已知函数f(x)=x3+3ax-1,g(x)=f'(x)-ax-5,其中f'(x)是f(x)的导函数.对满足-1≤a≤1的一切a的值,都有g(x)<0,若实数x的取值范围是____. 特殊与一般的关系反映了客观世界普遍联系的规律,因此数学解题中我们要充分利用二者的关系,将一般问题特殊化或者将特殊问题一般化来解决. 例4 已知(1-x)2(2x+1)5=a0+a1x+…+a7x7,则a0=____,a1+a3+a5+a7=____. 赏析由x∈R及式子结构特点,对x进行赋值. 令x=0,得a0=12×15=1. 常量与变量间的相等与不等关系是最常见的两种数量关系,它们在一定的条件下可以相互转化,既可以由相等关系得到不等结果,又可以由不等关系得到相等的结果. 赏析本题如果用纯用三角知识求解,过程较繁,认真观察式子的结构特点,引入柯西不等式,实现了从不等向相等的转化: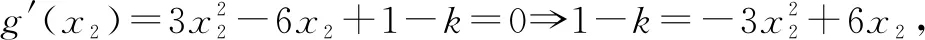
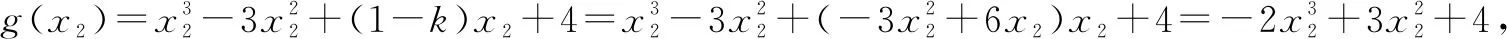
二、辩证思维中否定的否定在解题中的运用
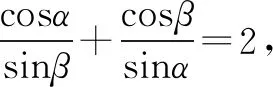


三、辩证思维中已知与未知的相互转化在解题中的运用
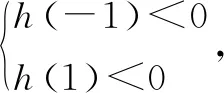
四、辩证思维中特殊与一般的转化

五、辩证思维中相等与不等的关系