构造法在抽象函数问题中的应用研究
刘建军
(新疆乌鲁木齐市第八中学 830002)
抽象函数尽管教材上没有提及,但是教辅资料上、高考试卷中出现了不少的关于抽象函数的题目.由于这类问题可以全面考查学生对函数概念和性质的理解,同时抽象函数问题又将函数的定义域、值域、单调性、奇偶性、周期性和图象集于一身,所以很受命题专家的青睐.尽管学生预学了,老师们也深入浅出地讲解了,但学生作业和测试时依然感觉困难,甚至无从下手.于是,我对此问题进行了深入思考和研究.事实上,解决有关抽象函数的问题,主要是依据题设进行恰当地构造,在此过程中,需要学生把握抽象函数的本质,并合理应用.下面我们一起来感悟构造法的魅力,体会抽象函数的“神秘莫测”.
一、抽象函数的概念
我们把没有给出具体解析式,只给出函数的特殊条件或特征的函数称为抽象函数.一般形式为y=f(x),有的还附有定义域、值域等,如:y=f(x),(x>0,y>0).
二、抽象函数的常见形式
2.正比例函数型:f(x+y)=f(x)+f(y);f(x-y)=f(x)-f(y).

5.周期函数型:f(x+T)=f(x)(T≠0).
三、构造法在抽象函数中的应用
1.构造方程
例1 定义在R上的函数f(x),对任意的x,y∈R,有f(x+y)=f(x)f(y),f(1)=2.求f(0)的值.
分析f(0)虽然是一个常数,但需要确定其具体值,因此我们可以将其看成一个未知数,依托题设“f(x+y)=f(x)f(y)”建立关于“f(0)”的方程.一个未知数只需一个方程,于是解法就确定了,令x=y=0即可求解.
解令x=y=0得,f(0+0)=f(0)f(0).
移项整理得,f(0)[1-f(0)]=0.解得,f(0)=0或f(0)=1.
下证f(0)≠0:
令y=0得,f(x)=f(x)f(0).若f(0)=0,则f(x)=0.此与f(1)=2矛盾.
所以f(0)=1.
评析本问题中应注意增根的甄别.学生可以从一次方程最多有一个根入手,但学生一般不具有这个理论高度.我们老师通常是在指数函数的性质“f(x+y)=f(x)f(y)”引导下注意到的.排除的过程也带有一定的经验主义,因此抽象函数教学应该遵循螺旋上升的原则.
2.构造特殊值
例2定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y∈R,有f(x+y)=f(x)f(y).求证:对任意x∈R,都有f(x)>0.
分析“当x>0时,f(x)>1”这个条件比结论范围更高,只能作为辅助条件使用,条件“f(x+y)=f(x)f(y)”的右端出现了乘积式,为构造平方式提供了机会,因此同一变量即可.进一步处理关键问题,排除平方式不为零,这需要精准构造.
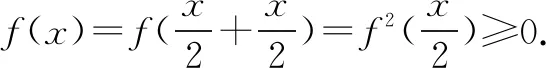
下面证明f(x)≠0:
假设存在x0∈R,使得f(x0)=0,则对任意x>0,有f(x)=f[(x-x0)+x0]=f(x-x0)f(x0)=0.这与已知当x>0时,f(x)>1矛盾.所以不存在f(x0)=0的情形.所以对任意x∈R,都有f(x)>0.
评析本问题难点是构造x0,并排除f(x0)=0,这需要深刻理解题设中的两个抽象等式,并合理运用.同时,构造不等式与排除特殊值要同时兼顾,否则都会陷入僵局.
3.构造单调性的定义式
例3定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y∈R,有f(x+y)=f(x)f(y),f(1)=2.解不等式f(3-2x)>4.
分析此不等式是由抽象函数构造出来的,必须利用函数的单调性解答.为此,要做两个准备.一是将右端的4等价变形为f(x0),这里的x0待定;二是证明本函数的单调性,这里务必紧扣单调性的定义.
解任取两个实数x1,x2,且x1
于是f(x2)=f((x2-x1)+x1)=f(x2-x1)f(x1)>f(x1).所以f(x)在R上递增.
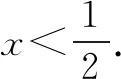
等价拆分x2.
评析本问题中对于初学者来说,不容易想到,必须深刻领会已知的“f(x+y)=f(x)f(y)”,构造出这种结构并恰当放缩才能得到定义所需要的f(x1),f(x2)的大小.
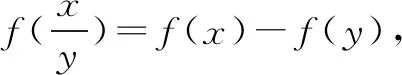
分析一般地,判断函数的单调性的方式是知道某区间内两变量x1,x2的大小的情况下,依据f(x1),f(x2)的大小,由定义判断而得.本题由于函数关系不明确,所以无法通过常规的方式解答,只能挖掘抽象关系,借助定义判断.
解f(x)在(0,+∞)上是单调递减函数.
下面证明之.

所以f(x2) 评析本问题中任取两正实数对于学生来说,很难想到,必须深刻领会已知的“当x>1时,f(x)<0”,并恰当构造“x>1”才能得到定义所需要的f(x1),f(x2)的大小. 4.构造奇偶性的定义式 例5 若定义在R上的函数f(x)满足:对任意的x,y∈R,恒有f(x+y)=f(x)+f(y)+1,求证:f(x)+1为奇函数. 分析本问题首先需要学生理清要证什么,其次才是怎么证明.将f(x)+1看作一个整体h(x),即h(x)=f(x)+1.要证h(-x)=-h(x),即证f(x)+1=-[f(-x)+1].解题过程就朝着这个目标前进. 证明令x=y=0,则f(0+0)=f(0)+f(0)+1,所以f(0)=-1. 令y=-x,则f(0)=f(x)+f(-x)+1,即-1=f(x)+f(-x)+1,所以f(x)+1=-f(-x)-1=-[f(-x)+1].所以f(x)+1为奇函数. 评析抽象函数奇偶性的判断,关键是探究f(x)与f(-x)的关系.往往需要通过赋值法扫除障碍,构造出所需关系式.分析法在解题中有重要作用.否则极易出现思路混乱,逻辑不清. 5.构造周期性的定义式 解因为f(x+6)=f((x+3)+3) (1) (2) 所以f(x)的周期T=6. 因为当1≤x≤3时,f(x)=x,所以f(1)=1,f(2)=2,f(3)=3. 所以f(1)+f(2)+f(3)+…+f(2020) 评析构造(1)式有一定的前瞻性.为了让抽象关系式中的负号消失,我们务必利用两次这个抽象关系式,可以理解为“负负得正”,进而构造出周期关系式.f(4),f(5),f(6)的计算也需要构造已知的抽象关系式. 6.构造中心对称 A.0 B.mC.2mD.4m 解由f(-x)=2-f(x)得f(x)-1=-[f(-x)-1],于是函数h(x)=f(x)-1是奇函数.而f(x)=h(x)+1的图象是由h(x)的图明向上平移1个单位而得. 所以f(x)关于(0,1)对称. 因此对于每一组对称点xi+xi′=0,yi+yi′=2, 故选B. 评析本题构造对称中心是关键,一个是已知函数,一个是抽象函数,依托已知函数去论证抽象函数,思路上是先猜后证.符合数学的研究规律.对学生的思维要求较高,不愧为是当年(2016)的高考把关小题. 7.构造轴对称 例8 已知函数f(x)(x∈R)满足f(x)=f(2-x),若函数y=|x2-2x-3|与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则所有横坐标和为( ). A.0 B.mC.2mD.4m 分析本题考查的知识点是二次函数的图象和性质,函数的对称性质.根据已知函数f(x)(x∈R)满足f(x)=f(2-x),分析函数的轴对称性,可得函数y=|x2-2x-3|与y=f(x)图象的交点关于直线x=1对称,进而得到答案. 评析y=|x2-2x-3|的对称性受翻折变换的掩饰,部分学生会“受骗”,不能很好地运用对称性化简问题.m的奇偶性对问题也有一定的干扰,使得f(x)=f(2-x)导出的对称轴难以发挥作用. 抽象函数问题本身比较复杂,我们在教学中应加强研究,研究学情,研究教法.本着螺旋上升的教育理念,我们可以在必修一第二章结束后安排这个内容.学生学完幂函数、指数函数、对数函数后,再学抽象函数,有助于学生对此概念理解,建议不在《函数及其表示》一节开展这方面教学.单元整体设计是突破这个难点的一种好办法,第二章的体例是先介绍函数的概念、定义域、值域、单调性、奇偶性、图象等函数通性,再通过三个重要初等函数:幂函数、指数函数、对数函数的学习加深对理论的理解,再从特殊到一般,研究抽象函数,教学效果应该不错.在这过程中,我们要注重数学思想与方法的渗透,如方程思想,消元法等.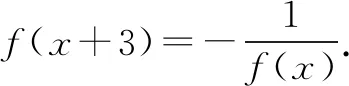


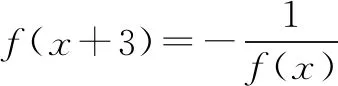
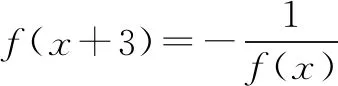
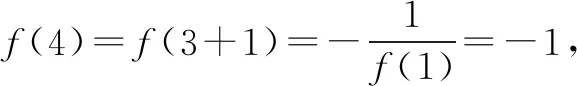
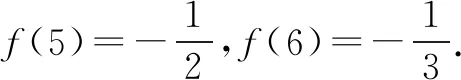
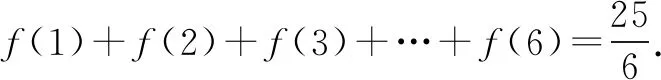

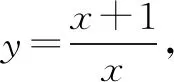
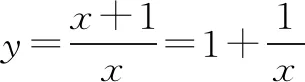
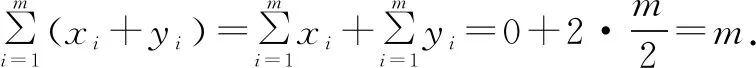
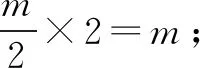
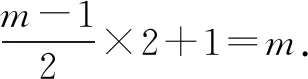
四、教学反思

