多思少算 追求高效——例谈高中数学多选题解题策略

蔡海涛

(福建省莆田第二中学 351131)

当前，数学高考在进行题型改革的创新，多选题即是其中一种新的题型.多选题突出了数学核心概念，强化了基础知识和基本技能的有效落实，考查了学生的理性思维.2020年高考山东、海南卷引入多选题，各有4道多选题，分值20分，情景新颖、思路开阔的多选题给高考试卷注入了生机和活力．解答多选题的基本思路是充分利用题目已知信息，排除干扰项，正确、合理、迅速地选出正确答案.多选题常见的解题技巧有直接法、排除法、特殊法、逆推验证法、数形结合法、构造法等，这些方法常常能够给解题提供“捷径”，达到事半功倍的效果.下面例谈多选择题的解题策略，旨在抛砖引玉.

一、直接法

直接从已知条件出发，通过推理、运算、验证得出正确选项的一种方法.

例1 (2020年高考山东卷·9)已知曲线C:mx2+ny2=1( ).

A.若m>n>0，则C是椭圆，其焦点在y轴上

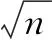
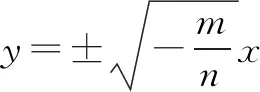
D.若m=0,n>0，则C是两条直线

点评本题的部分已知条件在四个选项中呈现，所以只能结合选项进行逐项分析求解，m>n>0时表示椭圆，m=n>0时表示圆，mn<0时表示双曲线，m=0,n>0时表示两条直线.

二、排除法

排除法是通过观察分析或推理运算选项信息，通过特例逐一剔除错误选项，从而获得正确的结论.

例2 (2020年高考山东卷·10)下图是函数y=sin(ωx+φ)的部分图象，则sin(ωx+φ)=( ).

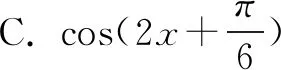
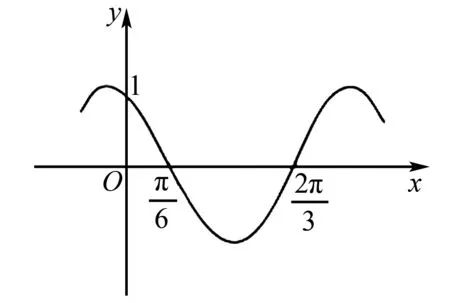
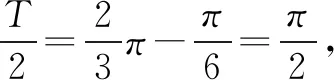
由于是多项选择题，故选BC.

点评多项选择题只须排除两个选项，即能得到正确答案.

三、特殊法

特殊法是借助特殊值或特殊图形、特殊位置替代已知的一般条件，得出结论，再进行验证，从而得出正确选项，实现“小题巧做”的解题策略.

例3 (2021年高三八省联考·10)设z1,z2,z3为复数，z1≠0.下列命题中正确的是( ).

A.若|z2|=|z3|，则z2=±z3

B.若z1z2=z1z3，则z2=z3

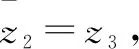
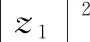
解析取z2=1+i,z3=1-i，满足|z2|=|z3|，但z2≠±z3，A错误；取z1=1+i,z2=1-i，满足z1z2=|z1|2，但z1≠z2，D错误.故选BC.

点评利用特殊法排除仅须找到一个反例即可，要判断一个结论成立还需要严谨的推理证明.特殊法常常与排除法结合起来使用.

四、逆推验证法

选择题的选项是已知条件呈现的另一种形式.通过对试题已知条件的分析，将各选择项逐个代入题干中，进行验证，以判断选择项正误的方法.

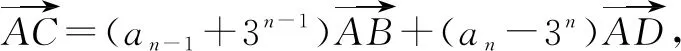
A.数列{an}为等比数列B.数列{an}为递增数列

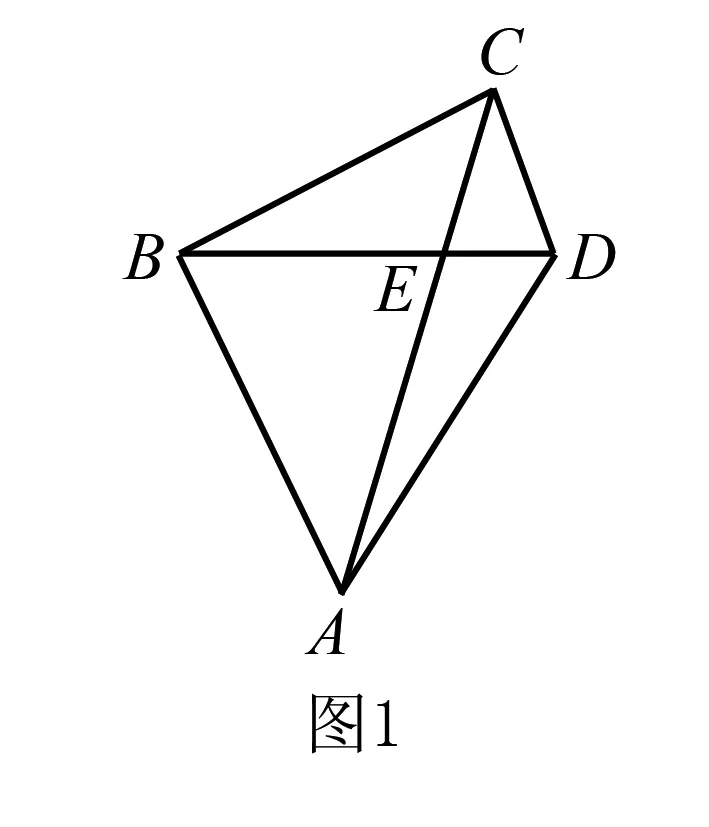
五、数形结合法

根据已知条件做出所研究问题的图形，借助几何图形的直观性作出正确的判断.

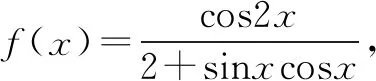
A.f(x)=f(x+π)

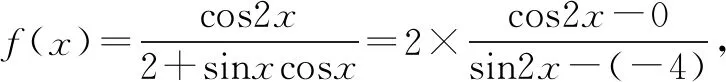
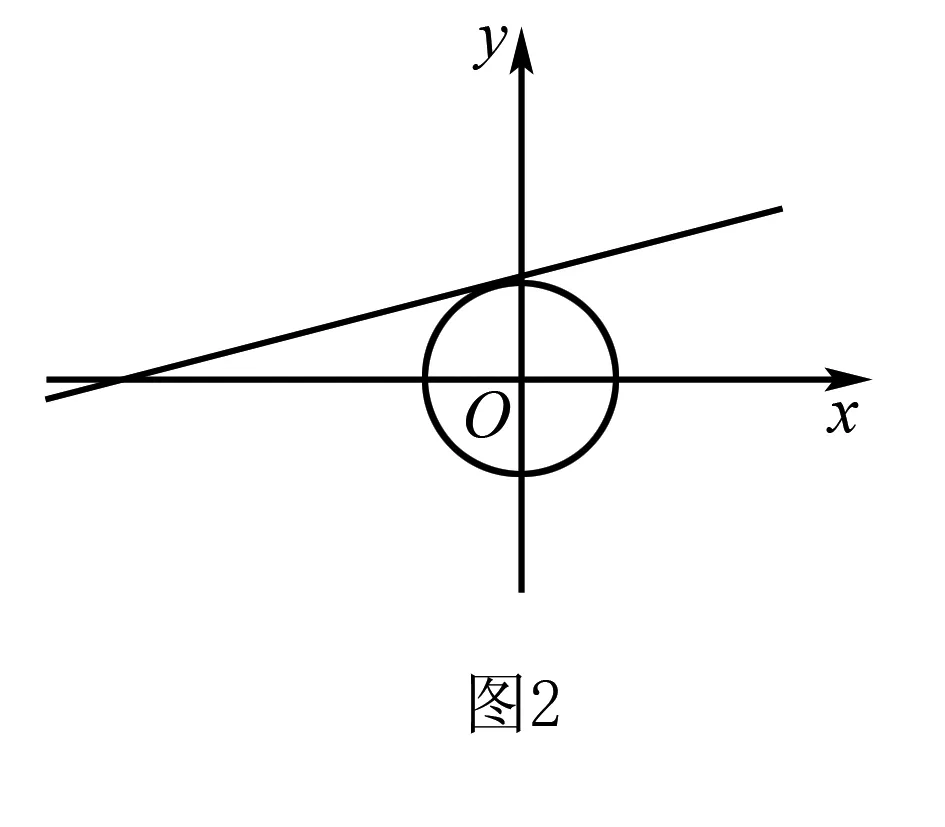
点评数形结合法是通过数与形的互相转化来解题，包含“以形助数”和“以数解形”两个方面.涉及函数、方程、不等式等问题，常考虑利用数形结合法.

六、构造法

构造法是根据问题已知条件给出的信息，将问题作适当处理，构造与问题相关的形式，揭示问题的本质，从而解题的方法.

例6 已知函数f(x)是奇函数，当x>0时，f′(x)-f(x)>1，f(1)=3，则( ).

A.f(4)>ef(3) B.f(-4)>e2f(-2)

C.f(4)>4e3-1 D.f(-4)<-4e2-1

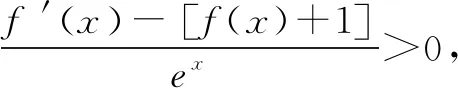
故选ACD.

点评解决本题中含有导函数的不等式，关键在于构造出某个函数的导函数，得出所构造的函数的单调性，从而比较函数值的大小关系.

总之，学生在解决多选题时需要多去思考已知条件的信息，抓住问题的本质，不要仅仅考虑问题表面直接解答，避免“小题大做”，要根据题意灵活多变地选择巧妙方法，随机应变地处理，从而达到“少算”甚至“不算”简单高效的目的.“多思少算”是数学活动经验的积累，并非是一种投机取巧，而是作为解题的“辅助手段”，但却不能作为解决问题的唯一路径，知识与方法才是基础，解题技巧以知识作为载体与依托，与基本知识及基本方法相辅相成，只有充分掌握双基，有意识地运用“多思少算”的策略去思考，多角度去探索，提高思维的广度和深度，让“多思少算”解题技巧发挥最大的成效.