关于高中生运用数形结合思想解题的实践

李小红

(福建省上杭县第一中学 364200)

运用数形结合思想解答数学习题，能达到简化计算，提高解题效率的目的.通过组织学生开展运用数形结合思想解题实践活动，使学生充分感受到了数形结合思想的好处，很好的提高了学生的应用能力.

一、运用数形结合解答向量习题

例1已知向量a、b满足|a|=1，|a·b|≥2，则|a-b|的最小值为( ).

A.4 B.3 C.2 D.1

解析∵|a|=1，不妨设a=(1，0)，b=(x，y)

∵|a·b|≥2，∴|a·b|=|x|≥2，则x≥2或x≤-2

又∵|a-b|表示向量对应点的距离，则如图1所示，由图可知，当a、b对应图中A、B两点，此时b=(2，0)时，向量对应点之间的距离最小，最小距离为1，选择D项.

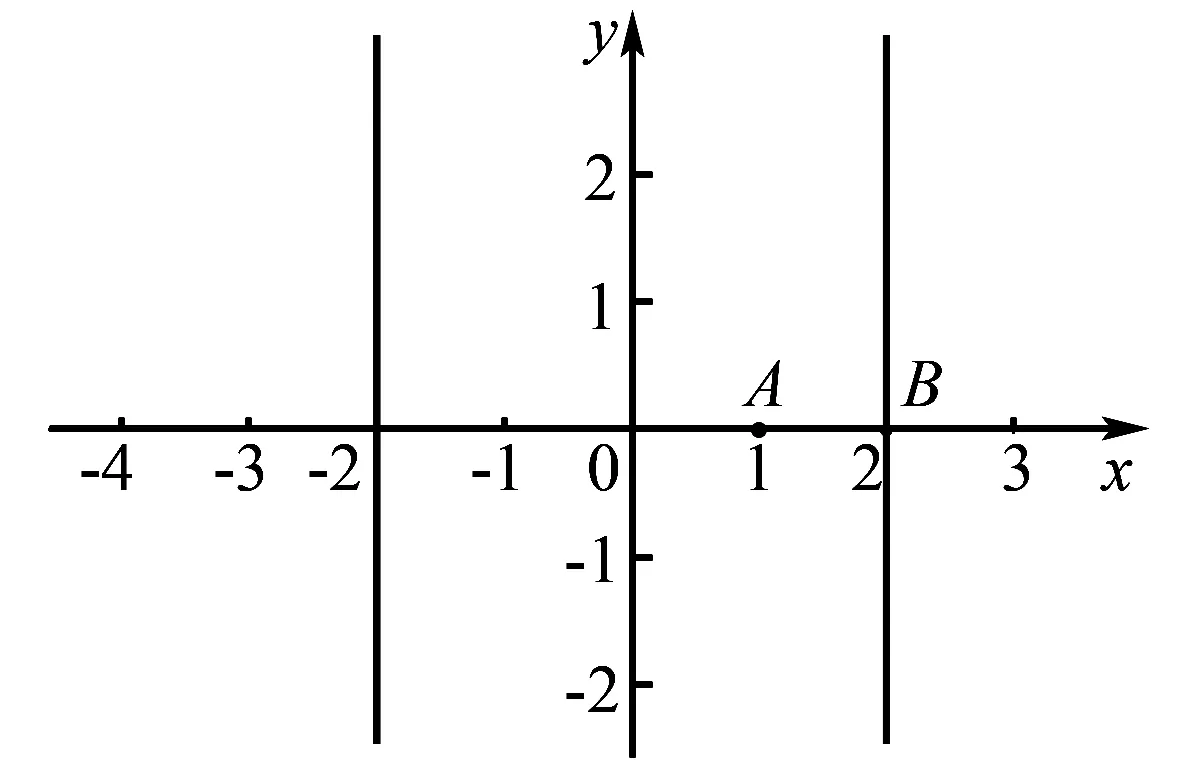
图1

实践感悟：运用数形结合思想将向量坐标转化为相关图形，可直观的看到相关参数之间的关系，降低了计算复杂度，提高了解题正确率.

二、运用数形结合解答函数习题

例2已知函数f(x)=lnx+(a-1)x+2-2a，若不等式f(x)>0的解集中整数的个数为3，则a的取值范围为( ).

A.(1-ln3，0] B.(1-ln3，2ln2]

C.(0，1-ln2] D.(1-ln3，1-ln2]

解析根据题意x>0，∵lnx+(a-1)x+2-2a>0，即，ax-2a>x-lnx-2，令g(x)=x-lnx-2，h(x)=ax-2a，下面研究函数g(x)的图象.

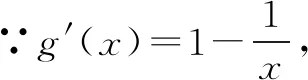
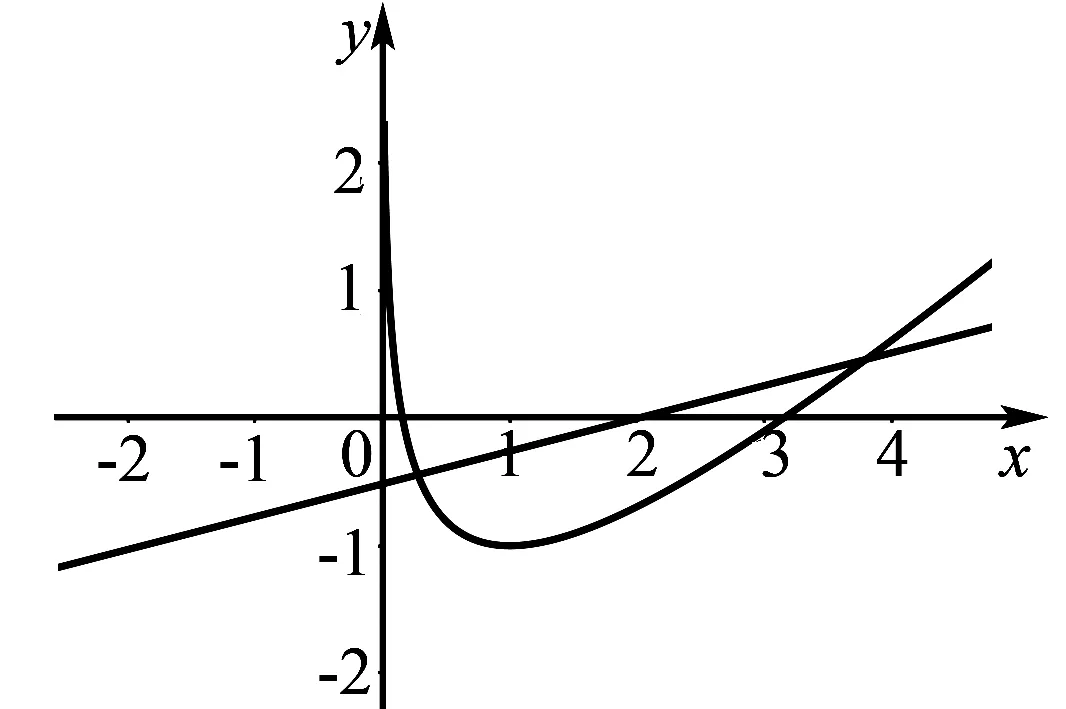
图2

实践感悟：运用数形结合思想分析、解答函数习题，可化抽象为具体，更容易寻找解题的突破口.

三、运用数形结合解答方程习题

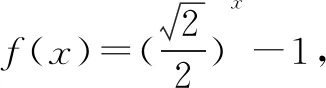
A.4 B.3 C.2 D.1

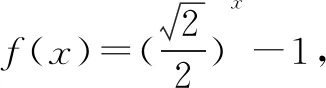
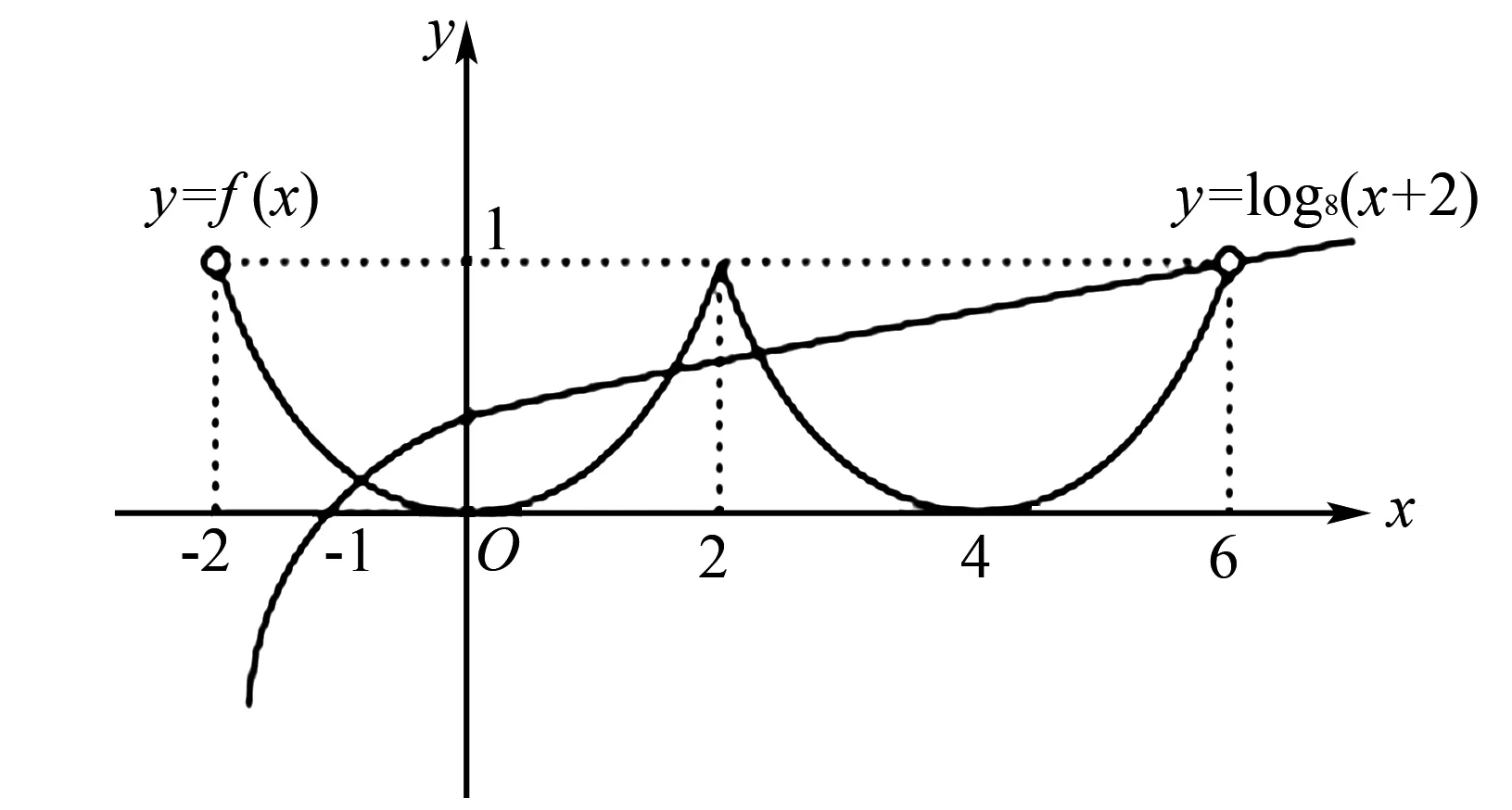
图3

由图可清晰的看到函数图象有3个交点，则方程根的个数为3，选择B项.

实践感悟：运用数形结合思想，将方程的根转化为对应函数图象的交点，方程根的个数一目了然.

四、运用数形结合解答几何习题

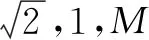
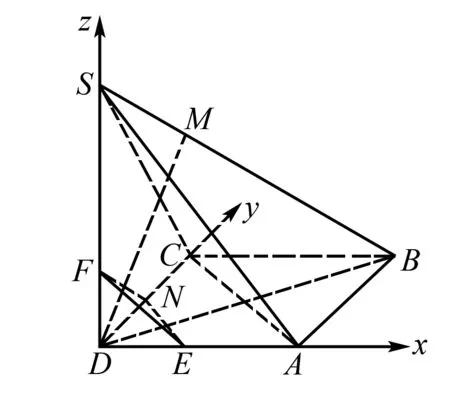
图4

又∵EN∩EF=E，∴DM⊥平面EFN，∴P点的轨迹，为△EFN.

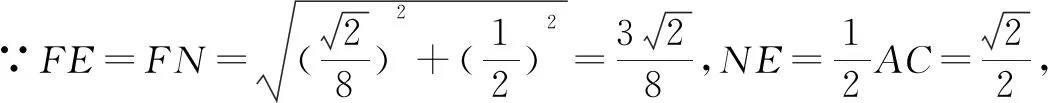
实践感悟：运用数形结合思想解答立体几何习题，可将复杂的空间关系转化为坐标运算，降低了解题的难度，提高了解题效率.

高中数学解题实践活动中，通过启发与引导，学生亲身体会运用数形结合思想解题的过程，认识到了数形结合思想的重要性，掌握了数形结合思想解答不同数学习题的思路，解题思维与能力得到了很好的锻炼.