巧借函数图像 解答数学难题

吴作成

(福建省石狮市第一中学 362700)

函数知识在高中数学中有着重要的地位，是学生学习中的重点和难点，也是高考中的必考内容.在高中数学解题中，传授学生解题技巧，灵活利用函数图像分析解题思路，提高学生解题效率.函数图像作为函数的重要表现方式，其价值和作用非常大，借助函数图像引导学生直观解题，节约学生解题时间，同时，利用函数图像分析问题，可以简化解题步骤，帮助学生更好的解题.因此，在高中数学解题教学中，让学生巧妙利用函数图像，体会数形结合思想，加强学生综合能力培养.

一、借助函数图像，掌握解题技巧

高中数学解题中，需要学生掌握一定的解题技巧，解决相应的数学难题.在函数知识学习中，函数图像解题是一种有效的解题方式和技巧，根据题目意思画出函数图像，通过对图像进行观察和分析，找出其中的数量关系，达到快速解题的目标.特别是在一些选择题和填空题.

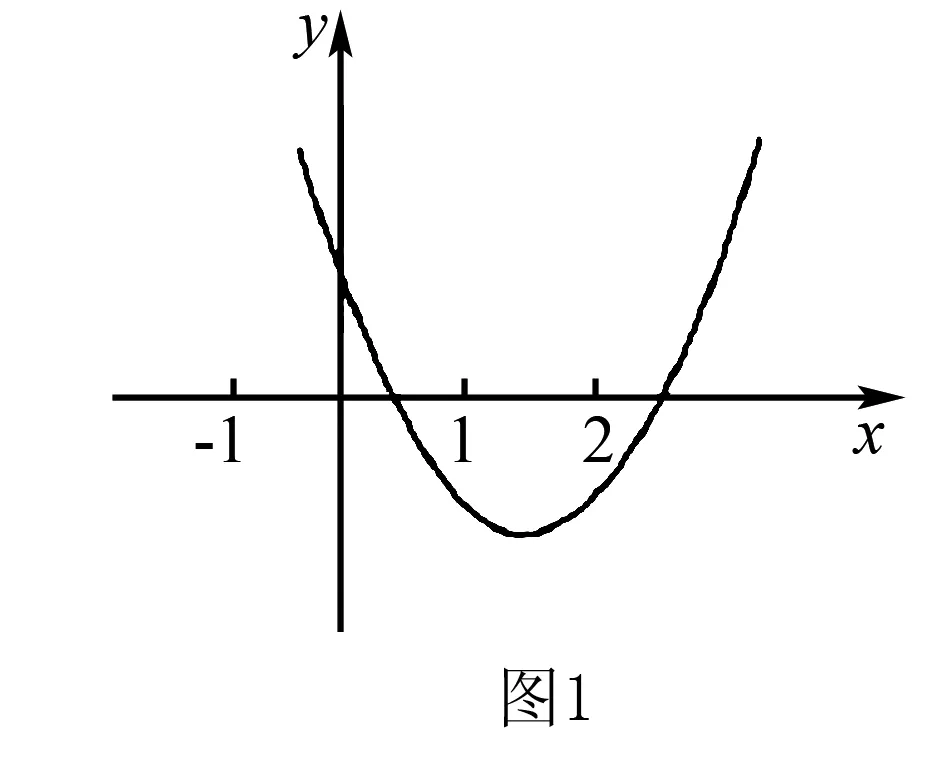
例题已知二次函数y=ax2+bx+c的图像如图1所示，判断下列代数式值的正负.①a+b+c②a-b+c.

在解题时，引导学生从函数图像入手，观察函数图像的开口方向、特殊交点，通过这样可以判断出a>0.在对两个代数式进行判断时，教师可以利用特殊值代入的的方式，帮助学生完成解题.当x=1时，那么y=a+b+c，，当x=-1时，那么y=a-b+c，根据这样可以找出其在函数图像中的坐标位置，如(1，a+b+c)、(-1，a-b+c).通过对图像进行观察，可以非常清晰的看到，x=1时，y<0，x=-1时，y>0，做出准确的判断.因此，高中数学教学中，教师需要利用函数图像解题，引导学生开展更多练习，找到更加有效的解题方式，提高学生的解题能力性，从而保证学生的解题效果和质量.

二、借助函数图像，加深数学思想体验

利用函数图像是高中数学解题中的重要方式，在数学问题中，其条件是通过数字和图形展示的，数与形之间有着密切的关系.高中数学解题教学中，培养学生函数图像应用思维，结合具体图像进行分析，完成数学难题解答.借助函数图像分析问题关键点，减少解题运算过程，为学生指明解题思路.同时，利用函数图像解题是数形结合思想的重要表现.

例题已知函数y=x2+x+a中，当x∈[-1,2]时，函数的最值之和是6，求解a的值.

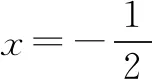
三、利用函数图像，开展分类讨论

高中数学解题中，利用函数图像对问题进行分析，找到题目中的障碍和迷惑点，准确把握解题关键点，完成数学问题思考和解答.在实际的解题中，要求学生根据函数表达式，准确画出函数图像，如果题目中存在多个函数表达式，需要采取分类讨论活动，讨论未知量的取值对函数结果的影响，进而完成数学题目的解答.

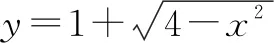
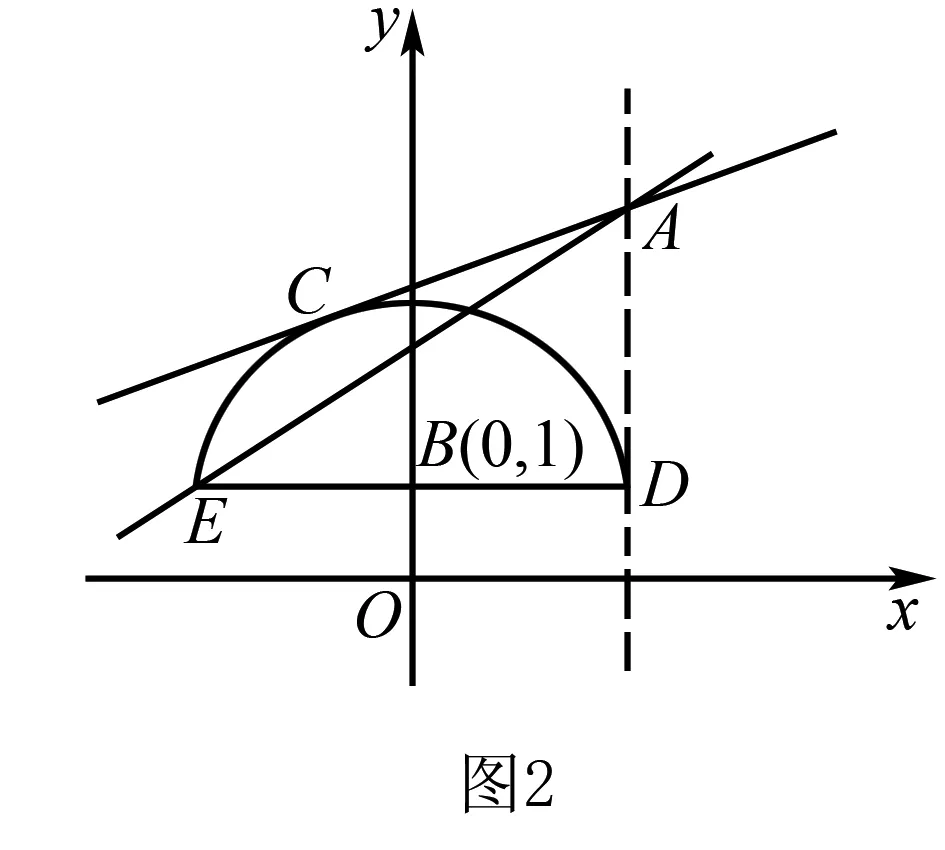
四、利用函数图像，优化解题方式

高中数学解题教学中，数学题目复杂多变，具有灵活性特点，面对相同的题目，学生可以采取不同的解题方式，虽然可以得到相同的答案和结论，但是，学生的计算量和计算步骤差异较大.利用函数图像解题，其本质就是借助数形结合思想进行解题，借助图像将问题展示出来，培养学生良好的作图习惯，利用函数图像寻找最佳的解题方式，保证学生数学解题质量.

例题求解满足不等式|x-5|-1<|2x-3|的x的取值范围.

在解题的过程中，在去绝对值时，常常会出现一些问题，使得学生解题结论不准确或者不全面等问题.为了帮助学生解题，教师可以将不等式左右两边分别转化成函数y=|x-5|-1和y=|2x-3|，然后画出相应的函数图像，通过对函数图像进行观察和分析，可以非常清晰地找到不等式成立的情况，即函数y=|x-5|-1的图象在函数y=|2x-3|的下方.通过这样的方式进行解题，可以简化学生解题步骤，提高学生的解题效率，优化学生的解题方式，提高学生的解题能力.

五、利用函数图像，转变解题方向

学生在初中数学学习时已经接触函数知识，了解一些初等的函数类型和知识，是学生高中函数知识学习基础.高中数学解题教学中，函数知识学习的最终目的是解决实际问题，根据问题构建相应的数学模型，将函数图像作为数学问题解题工具.作为高中数学教师，应当引导学生灵活利用函数图像，明确数学问题的解题方向，完成数学问题的思考和解答.

例题求解不等式|x+2|-|x|>-1.

一般来说，学生在解题时，常常会想到对不等式进行移项、平方，然后开根号进行处理，虽然可以解决题目，但是，随着不等式问题的复杂，此种解题方式使得解题过于复杂，影响学生解题效率.结合常规思路的思考，开展相应的讨论活动，引入相应的函数图像.在解题中，对不等式进行移项，转化成|x+2|>|x|-1，构建相应的函数，画出相应的函数图像，对其进行观察和分析，找出函数的交点，完成不等式问题的思考和解决.

高中数学教学中，不仅仅要求学生掌握数学知识，还需要学生掌握解题方法，结合相应的习题训练，不断归纳和总结解题技巧，更好的解决数学难题.