地铁紧急制动踏面热应力分析研究

应何蓉， 颜晓雨， 丁 宁， 朱凡宇， 连盛荣， 胡 艳

（江苏师范大学机电工程学院，江苏徐州221000）

0 引 言

列车制动能力的强弱是列车制动系统正常运行的一个重要衡量标准。目前，踏面制动仍是我国地铁列车主要制动方式之一，其制动的工作原理主要是通过车轮踏面与闸瓦之间的轮轨摩擦，将闸瓦与轮轨间的动能转化为热能。车轮踏面制动是现阶段国内地铁列车使用频次最高、效率最高的一种制动方式。以成都1号线一期为例，全长18.5 km，全部为地下线，设17座地下车站，平均每3 min实施一次制动停车。车轮踏面循环承受由制动产生的热量及其与列车轨道摩擦产生的摩擦热，导致车轮温度呈周期性急剧升高，引起制动车轮产生热应力裂纹。同时，车轮由于循环受热产生热疲劳导致其疲劳磨损加剧。严重的磨损不仅影响列车运行的平稳性及安全性，而且会给列车的后续维护、保养带来很大的困难。正确分析踏面制动装置的温度场和应力场分布，对于延长轮轨的使用寿命以及降低运输成本都有重要的意义。

国内外众多学者对列车踏面制动热效应进行了研究。Parker等［1］20世纪40年代已开始对制动时车轮踏面热斑演变的情况进行研究。20世纪下半叶此类研究逐渐多样化，Pigors［2］根据磨损的几种基本定义，分析了钢轨和轮毂元件所承受的应力。对塑性变形、运行表面和磨损特性进行了大量的研究。当车轮或轨道的外表面因材料与周围的大气接触而发生变形时，就会发生部分氧化。氧化后的金属颗粒就会被磨掉。磨损常常受到工艺本身的特性或蹄式制动器产生的马氏体层的影响。Barber［3-4］对滑动系统进行热弹性建模，分析确定了不稳定性的开始和临界滑动速度。文献［5-7］中利用有限元方法，将热弹性接触稳定问题归结为固定状态的特征值问题。文献［8-9］中对鼓形制动器和铁路盘式制动器进行了高能量滑动接触的轴对称有限元分析。Vernersson［10］建立了轮缘与闸瓦相互作用的理论和数值模型。Teimourimanesh等［11］主要针对地铁车轮的车轮温度及疲劳强度在不同辐板情况下进行了研究。张萍等［12］利用有限元分析的方法，研究了在移动热源和均布热源2种不同热流密度加载方式下，制动过程中车轮踏面沿径向的温度和应力变化。张野等［13］利用有限元方法建立车轮紧急制动的三维弹性模型，研究了表面换热系数和轴重等因素对紧急制动温度的影响。文献［14-15］中等则研究了不同硬度的闸瓦在连续2次紧急制动时踏面温度与热应力的变化。以上研究都为地铁紧急制动踏面热应力的分析研究奠定了基础。

地铁列车车轮踏面温度和应力分布对车轮寿命及制动性能有着极其重要的影响。本文将通过有限元分析软件Abaqus建立车轮-闸瓦摩擦耦合模型，模拟仿真地铁列车紧急制动过程中摩擦耦合系统温度变化。探讨车轮踏面温度和应力传递状况，为研究车轮踏面热磨损及热疲劳可靠性提供依据。

1 模型的建立

1.1 模型参数

地铁列车车轮主要使用840D车轮，闸瓦主要使用铸铁闸瓦、合成闸瓦。本文将使用840D车轮-高磨合成闸瓦进行建模分析。车轮直径为840 mm，轮辋厚度为65 mm。840D车轮具体尺寸参数见表1。车轮与闸瓦材料参数见表2。车轮-闸瓦三维耦合模型如图1所示。

表1 840D车轮基本尺寸 mm

表2 车轮与闸瓦材料参数

图1 车轮-闸瓦三维耦合模型

1.2 制动工况的确定

计算初始条件：制动车轮的半径为420 mm。本文计算制动初速度v为80 km/h时紧急制动车轮踏面的温度场；我国高速及快速列车的紧急制动减速度可定为0.08～0.10 g［16］，最大不宜超过0.12 g。普通旅客列车可取为0.08 g，货物列车可取为0.06～0.07 g。本文地铁列车紧急制动减速度取0.08 g，对应制动时间为28.34 s。

1.3 制动盘对流换热系数的确定

气流通风散热是列车车轮踏面制动散热的主要形式。车轮的散热系数受很多因素影响，主要是由换热界面的形状和气流状态。纵观整个制动过程，车速和踏面温度不断发生变化，它们的对流换热系数也随之改变。

根据高速列车轴盘制动的经验散热数据

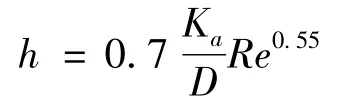
式中：Ka为空气导热系数，取26.24 mW/（m·K）；D为制动盘外径；Re=ωR2/ua为雷诺数；ω为制动盘角速度；R为制动盘半径；ua为空气动力黏度，取17.9 μPa·S。

当Re＞2.4×105时，气流形式将变成紊流，换热系数可表示为：

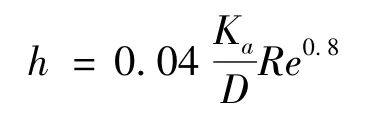
当速度大于20.27 m/s（即72.9 km/h）时，h=6.85·ω0.8W/（m2·K）；当速度小于20.27 m/s（即72.9 km/h）时，h=5.98·ω0.55W/（m2·K）。由于制动盘与轮廓连接处的热传导很小，于是假定其表面是绝热的；同时由于闸片的传热性能较差，其离摩擦表面较远的面（即压力的施加面）也认为是绝热表面，表3列举了模拟过程中选取的速度以及其对流换热系数。

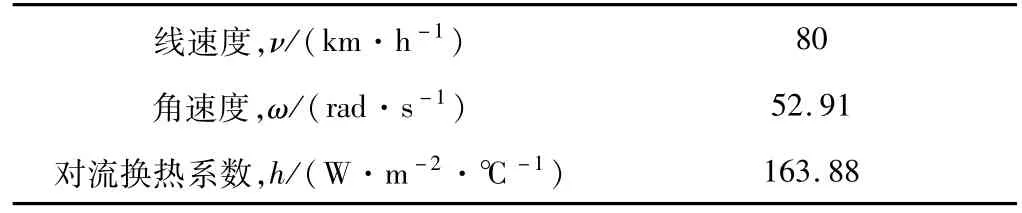
表3 数值模拟速度设置及其对流换热系数

2 仿真结果

2.1 紧急制动下车轮温度场分析

只有准确获得地铁列车在紧急制动工况下，车轮温度场随时间变化及分布规律，才能更有效地研究车轮踏面制动热应力耦合问题。

以地铁初速度为80 km/h制动距离为800 m的仿真作为研究对象，由图2可知，最高温度区域在车轮踏面上，随着制动时间的推移，制动结束后热量从踏面向其他连接制动辐板的区域传递。

图2 车轮踏面温度云图

在车轮踏面上沿径向选取如图3所示的9个节点，温度曲线如图4所示。在车轮踏面沿轮辋方向选取如图5所示的14个节点，其温度曲线如图6所示。

图3 踏面径向9个节点分布

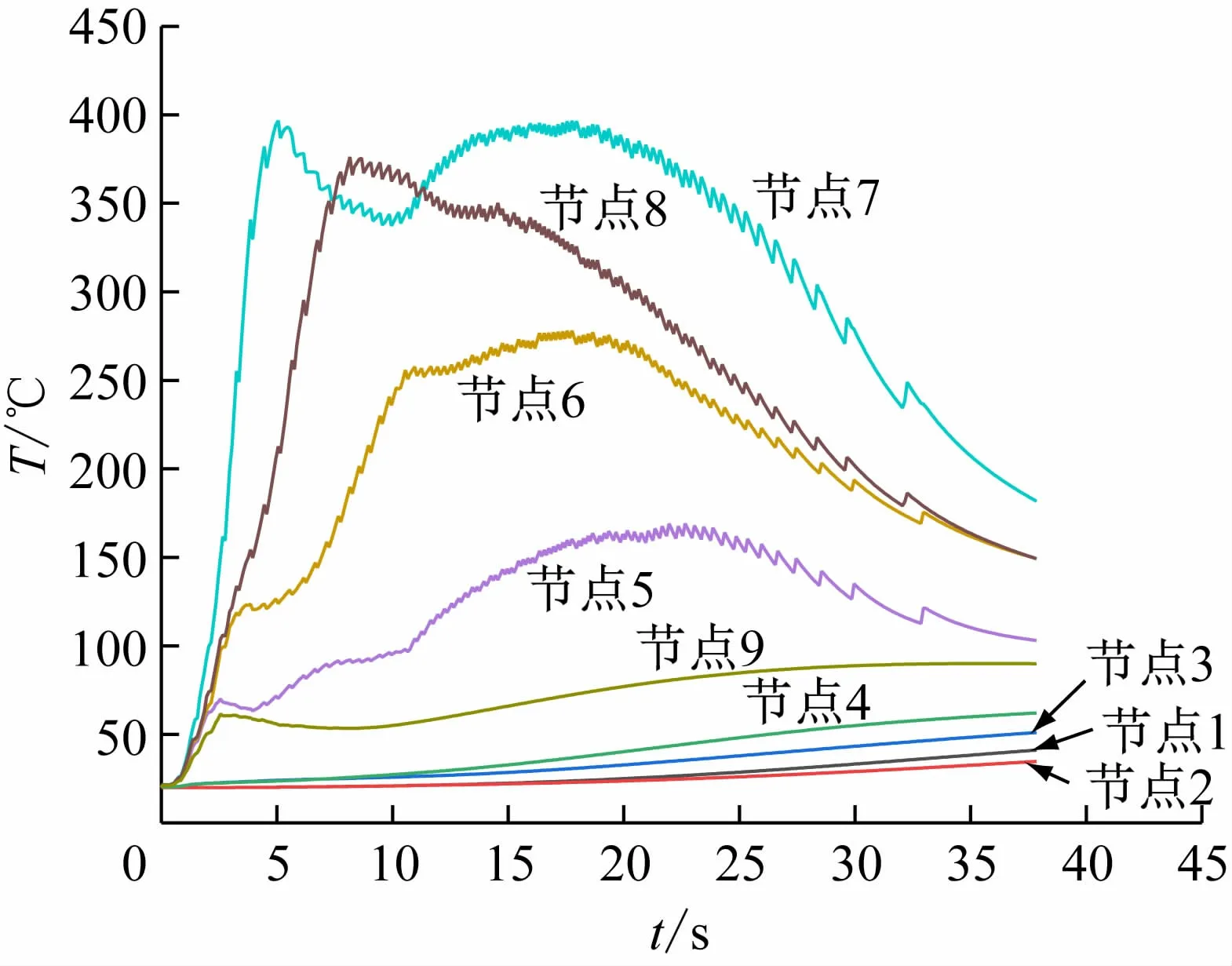
图4 车轮踏面不同节点温度曲线

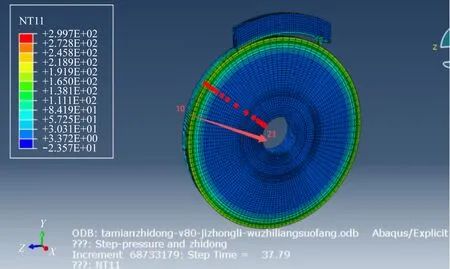
图5 沿轮辋方向14个节点分布

图6 沿车辋方向不同节点温度曲线

通过研究车轮踏面温度曲线可知，随着制动开始，车轮的温度从20℃的初始温度开始上升，在接近制动结束的时候，温度上升速度逐渐减缓且趋于稳定，热量传递过程是由踏面到其他连接部位且最高温度出现在踏面中心处。在踏面部分产生最高温度的原因除了其接触面积最小之外，还因该部分的热流最为密集，所以热量很容易累积，这也是温度降低速度缓慢的原因。

由图6可知，温度由车轮踏面位置处向轮辋方向传递，呈梯度分布。

2.2 紧急制动下车轮应力场分布

以上节点沿踏面方向的应力曲线如图7所示，沿轮辋方向的应力曲线如图8所示。由图7可见，应力有着与温度随时间变化一样的趋势，温度高则对应的应力大，但在接近辐板的节点处不满足此规律，主要是因为辐板属于车轮的强度薄弱部位，应力较为集中，越接近辐板位置的节点，其应力值越大。由于温度越高引起的热应力值越大，对车轮表面以及闸瓦表面的材料影响越大，所以闸瓦散热性能的优化设计在后续研究中应进行考虑。在制动初速度为80 km/h时，制动运行至5.3 s时，车轮踏面中心处出现最大热应力，为470 MPa。

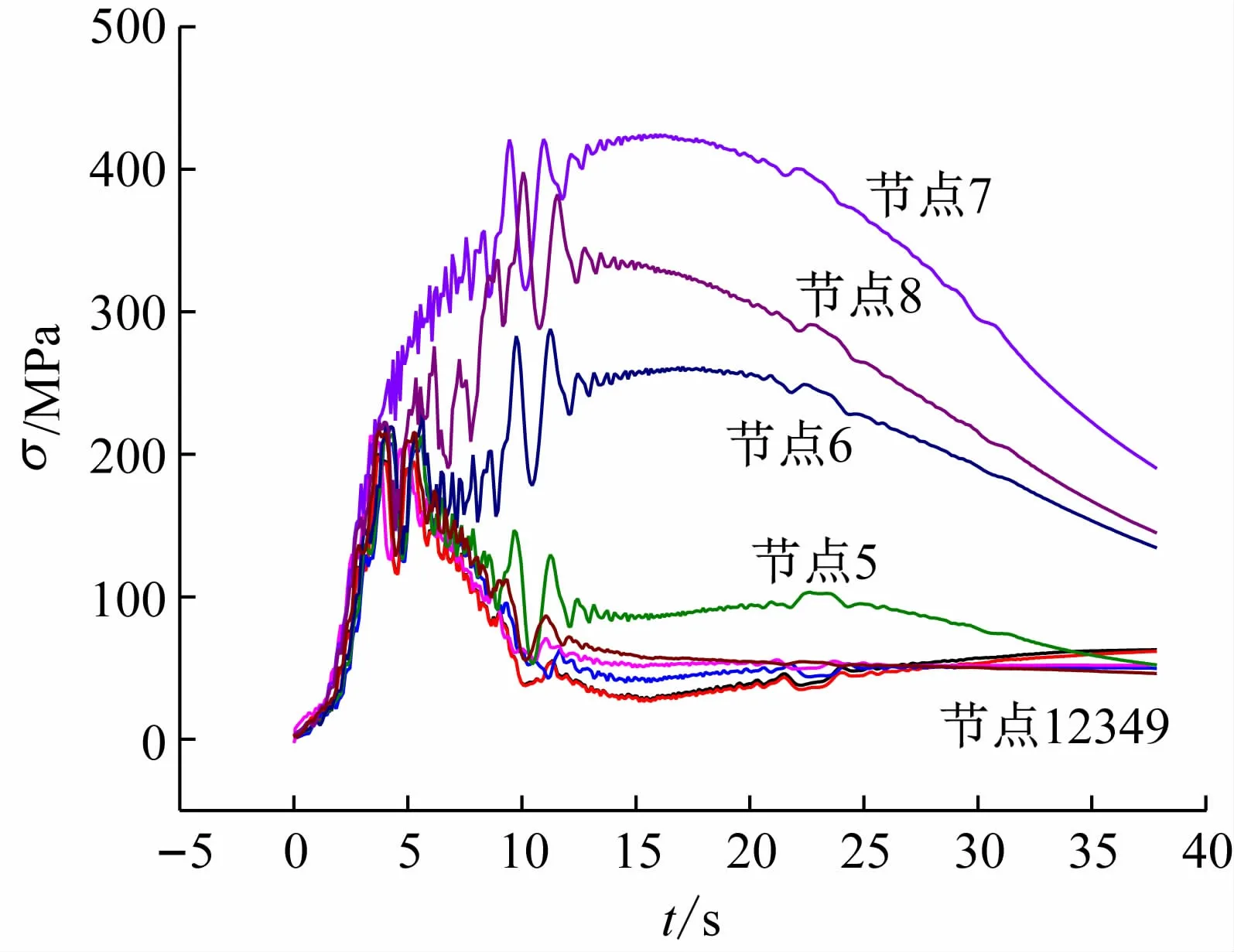
图7 踏面应力分布曲线

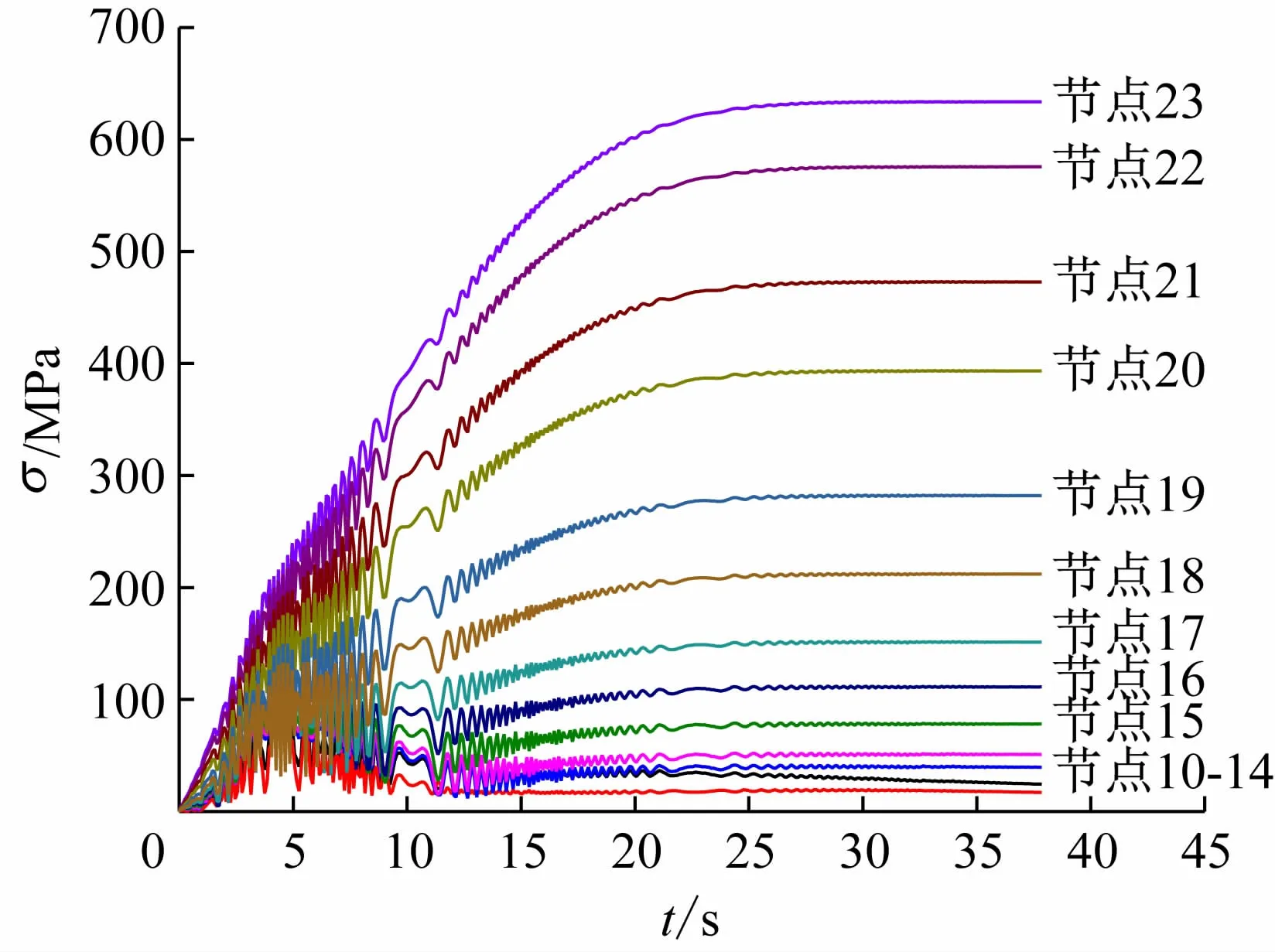
图8 径向应力（σ）分布曲线

由图8可见，应力值沿轮辋方向呈梯度分布，应力值不断增加。在制动刚开始时，越靠近轮辋处其应力值增长越快，接近制动结束时，应力值逐渐趋于平稳。由于在接近轮辋处存在形状改变，产生了应力集中现象，以及零件表面与介质之间换热面积大，换热量大，所以沿径向的应力值普遍高于踏面应力值。

由图5、6可知，在紧急制动过程中，动能损失的能量，将转化为车轮与轨道摩擦产生的热量，热量会一直在踏面累积，踏面传递到各个与其接触的部分。在该过程中，开始的时间段，接触面温度最高，随着时间推移，可以从图中发现，在制动逐渐接近结束的时候，最高温度的部分已经不再是接触的踏面了，而是逐渐趋于其他连接部位，但是整体的温度也会随之降低。制动完全停止之后，也就是制动到静止的时候，没有了外部能量的输入之后，所有的能量将会传递给周围的空气以及其他介质，研究对象的温度就会整体逐渐降低，其中因为温度上升引起的热膨胀也会随之减小，最大的热应力也迅速下降。

3 结 论

本文主要研究的是地铁列车踏面制动装置的制动热分析，建立踏面制动装置热应力耦合接触模型；利用Abaqus有限元分析软件在制动初速度为80 km/h时紧急制动工况下对车轮踏面的热分析、热负荷进行模拟，通过研究分析其温度场及热应力场，得到了如下结论：

（1）紧急制动过程中的车轮踏面处，是所有车轮部位中温度最高的区域，因为能量转化主要是由该部位进行，车轮的动能减少大部分都是转化为该部分的摩擦热能。该接触面的温度变化是先迅速上升，再缓慢趋于最大值，之后再缓慢冷却。在制动初速度为80 km/h，制动运行至5.5 s时，车轮踏面中心处出现最高温度为390℃。

（2）在进行紧急制动之后的一段时间内，温度在该时间内可以达到最高，而且平行对比不同位置的情况发现车轮踏面中部温度最高，两侧的温度较低。在达到温度最高值之后，车轮踏面中部温度缓慢降低，而车轮踏面两侧温度降低较快，这是因为中部热流最为密集且接触面积小，所以温度降低缓慢，两侧温度降低较快，越靠近两侧温度降得越快。

（3）制动刚开始的一段时间，最大的热应力一般也是出现在车轮踏面的位置。在制动初速度为80 km/h时，制动运行至5.3 s时，车轮踏面出现最大热应力为470 MPa。