测量不规则块体界面摩擦角的滚筒实验

汪 远， 邓检良， 黄凤荣

（1.上海交通大学船舶海洋与建筑工程学院，上海200240；2.上海勘察设计研究院（集团）有限公司，上海200093）

0 引 言

滚石是一种全球性的山地地质灾害，具有突发、快速、强致灾等特性，每年因滚石灾害引发的生命、财产安全事件数以万计。目前国内主流的对滚石的定义为：个别块石因某种原因从地质体表面失稳后经过一定的运动方式沿着坡面向下快速运动的岩体［1］。其运动方式主要包括滚动、滑动、碰撞、坠落、弹跳或以上几种的组合，主要以直接冲击和间接堆积的方式对其范围内的人与物构成损害和威胁。

目前，对滚石的研究主要涉及其运动特征以及其与结构物的冲击作用。如陈宇龙［2］分析了影响滚石运动轨迹和能量转换的诸多参数，认为界面摩擦角决定了滚石运动的轨迹和能量损失的大小。傅少君等［3］研究了滚石运动的影响因素，其主要包括边坡条件、块体条件以及滚石与坡面的相互作用（碰撞恢复系数、界面摩擦因数，入射角，入射速度等），并就滚石形状对运动加速度以及运动方式的影响进行了探讨，认为长条状滚石平均加速度最小，薄片状滚石平均加速度最大；块体形状越趋近球体，滚动能力越强。此外，代婧瑜［4］研究了滚石与边坡的界面摩擦角对滚石运动水平距离，滚石与防护结构碰撞时的能量的影响，结果表明对于坡角为70°，坡面为光滑且坚硬的基岩面的凹型边坡时，界面摩擦角与滚石水平运动距离、碰撞时的能量均呈负相关；且当坡角为40°时，界面摩擦角对滚石运动水平距离的影响最显著。胡厚田［5］总结了界面摩擦角取值的影响因素，其中包括坡面特征及滚石自身性质。

以上研究表明，滚石的运动复杂，其中滚石与坡面间界面摩擦角（界面摩擦因数）是表征滚石运动特征的重要参数，其取值与多个因素相关，但目前对不规则块体运动状态下的界面摩擦系数的系统的实验研究甚少。为此，本文以形状不规则的石英石块体为例，基于滚筒实验实测具有统计学意义的块体与滚筒底面之间的界面摩擦角［6］并分析其影响因素，最后采用DEM方法验证了实测的平均界面摩擦角可作为滑动摩擦因数用于数值模拟。

实验步骤主要包括：①摄影记录滚筒旋转过程中的块体运动情况；②数据处理阶段测量块体对应的圆心角。滚筒在竖直平面内以一定的转速（15、30、45或60 r/min）旋转一段时间后，筒内单个块体的运动达到稳定状态，摄影机记录下块体的运动情况。在数据处理阶段，基于AE软件的动态目标跟踪功能，确定块体在滚筒内运动轨迹的最高与最低点及其所对应的圆心角大小（见图2），以该圆心角为依据进行进一步的分析。

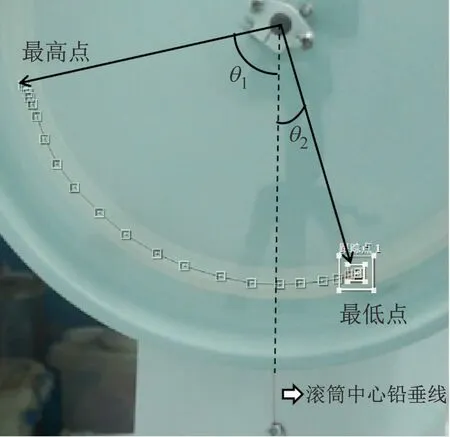
图2 块体滑动轨迹最高与最低点所对应的圆心角

1 滚筒实验方法与结果分析

1.1 实验装置与步骤

如前所述，滚石试验困难，其主要原因是滚石的速度等因素不受控制，本文通过采用滚筒试验，可以较好地控制滚石与底面之间的相对速度。本项目试验的主要思想是将野外的滚石的绝对运动转化为室内试验中的滚石与底面之间的相对运动，进而测定其界面摩擦角。

试验所采用的滚筒实验设备［7］（见图1）由三部分组成：滚筒、电动机及控制装置、摄影系统。其中旋转滚筒直径（内径）29 cm，筒宽6 cm，滚筒材质为有机玻璃。动力由电动机提供并由计算机控制，在块体稳定运动状态下，其相对速度v≈ωr（r为滚筒半径，ω为角速度）。摄影机的中心对准滚筒中心的铅垂线，摄影频率为50帧/s。

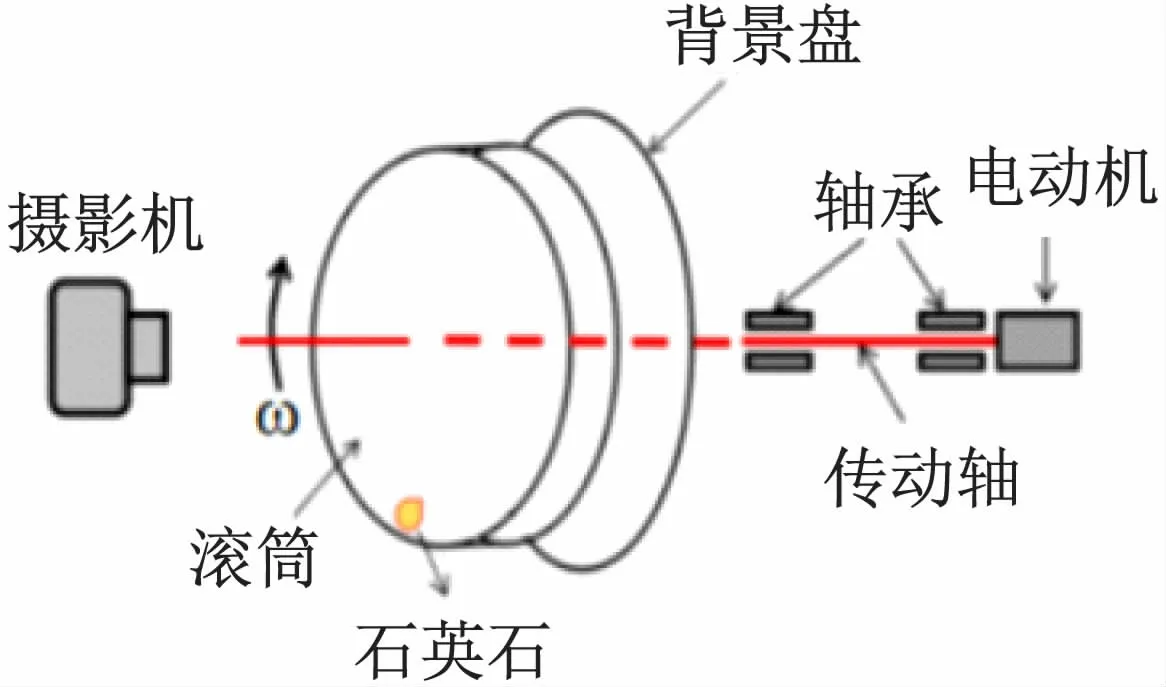
图1 实验设备示意图

1.2 实验物料

本实验选取的实验物料为6个不规则石英石块，为便于图像分析，石块表面着色。实验前后，用于着色的涂料无明显脱落现象。石块弹性模量为100 MPa［8］，泊松比为0.25［9］，密度为2 650 kg/m3。石英块的几何尺寸长为a，宽为b，高为c，且a≥b≥c，各石块的尺寸列于表1。所用石英块形状分别为薄片、方形、长条，如图3所示［9］。此外，为研究质量对平均界面摩擦角的影响，相似形状的石块选用两个质量悬殊的大块体和小块体，因此块体总数为6个。

图3 不规则石英石块样本

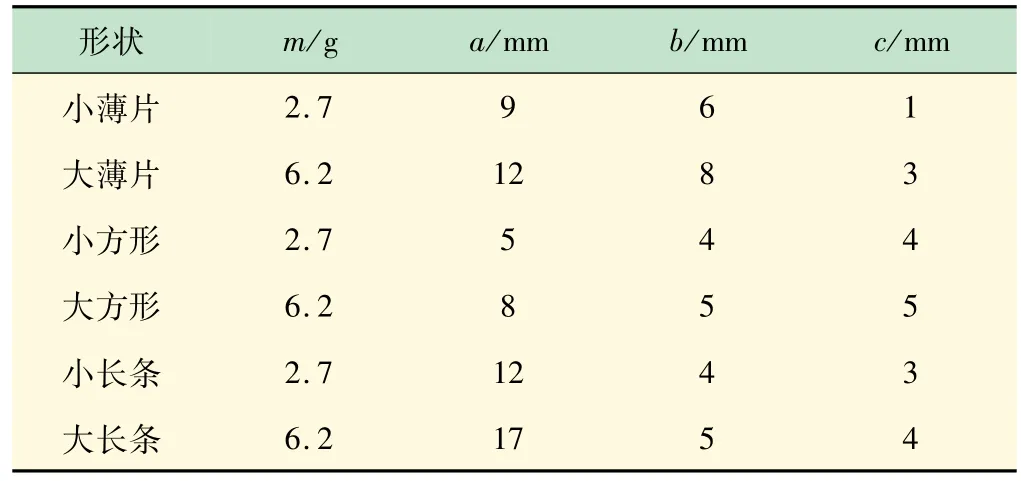
表1 不规则块体形状、质量及尺寸参数

1.3 实验结果

滚筒旋转一段时间后，筒内块体运动达到稳定状态，此时块体会在滚筒一定角度范围内往复振荡。在后处理阶段根据摄影记录采用AE软件跟踪块体运动，提取块体的位置坐标，测量块体往复振荡过程中的圆心角（见图4），以及最高与最低点所对应的圆心角（见图2）。实验结果表明，滚筒转速越大，最高与最低点所对应圆心角的幅度差也越大（见图5～7），即块体振荡幅度越大，而且幅度没有降低的趋势，因此取最高点峰值圆心角与最低点谷值圆心角的一半连续振荡20次所得的平均值作为平均界面摩擦角（见表2）。

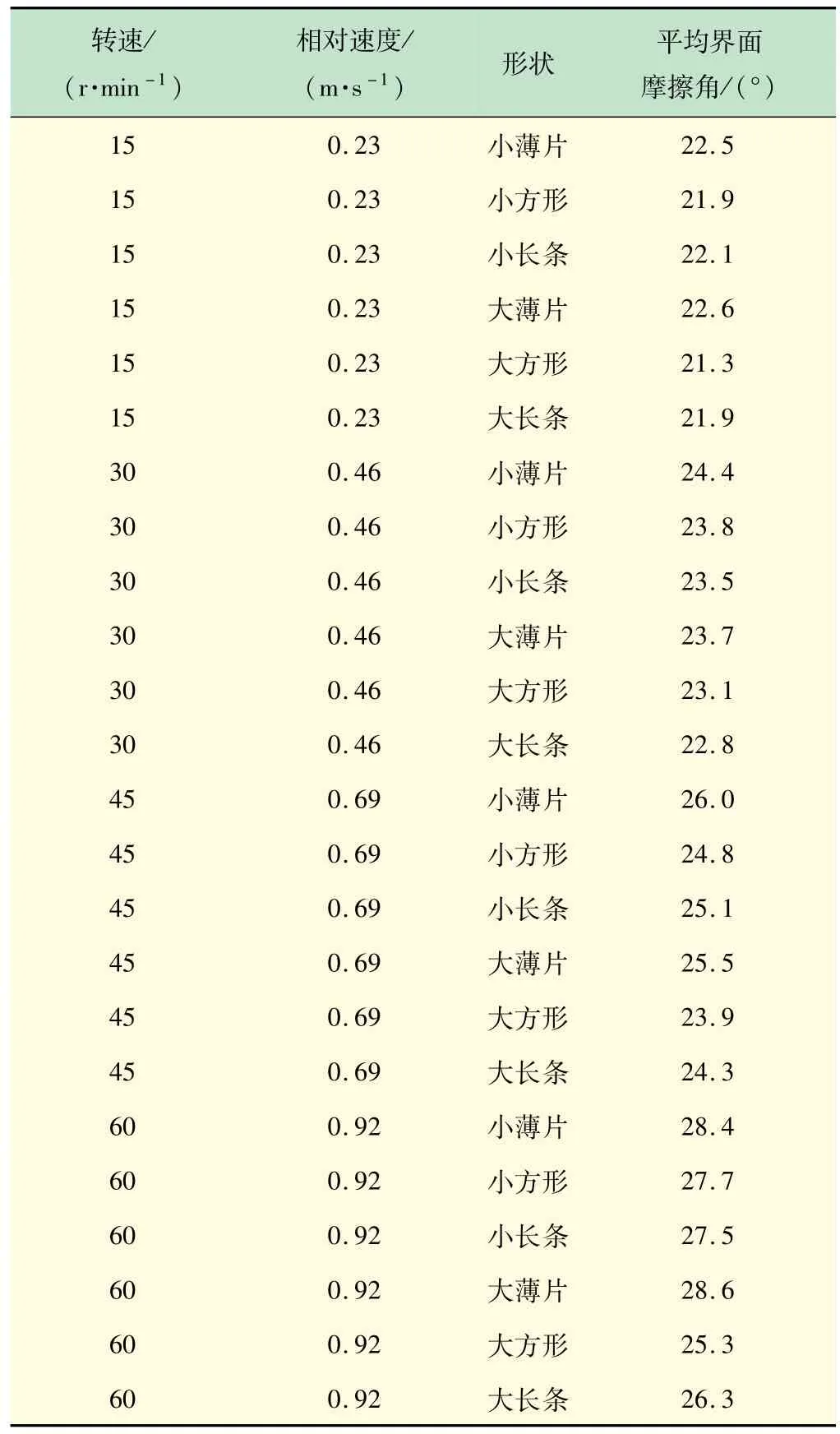
表2 平均界面摩擦角测试结果

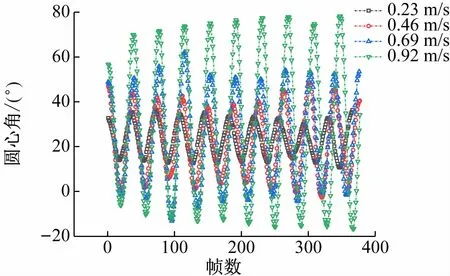
图4 典型的振荡运动（大薄片）

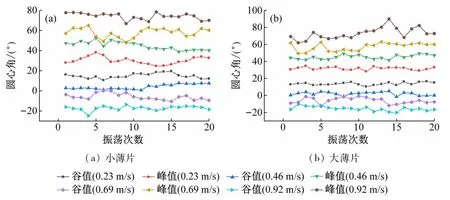
图5 薄片状石英块体的大小对圆心角的影响

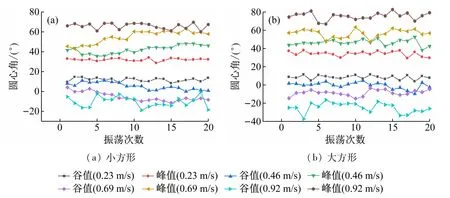
图6 方形石英块体的大小对圆心角的影响

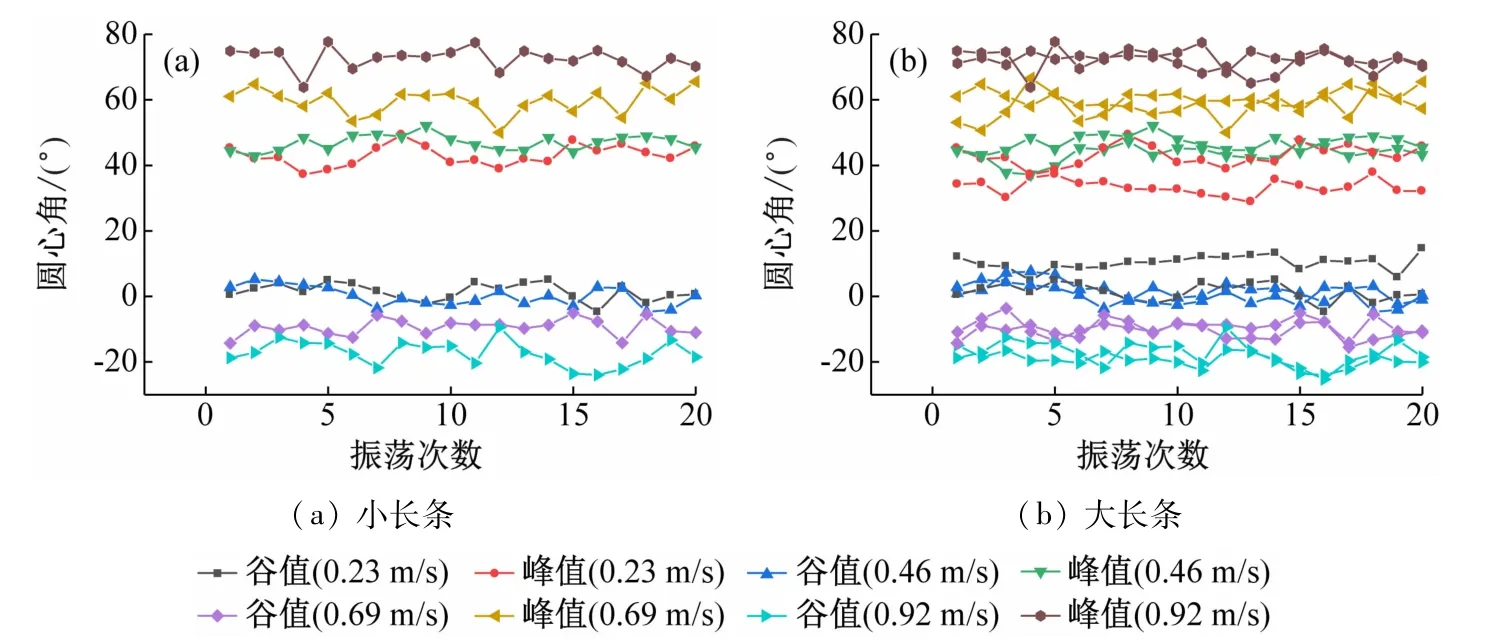
图7 长条形石英块体的大小对圆心角的影响

需要说明的是，对于方形块体来说，当相对速度较大时（如0.92 m/s），滑动状态会伴随间歇性的滚跳运动，即块体从最高点启动滑行到中间某位置处时开始出现向上弹跳现象，待弹跳结束会继续滑动。可能由于这种滚跳运动，测得的圆心角波动较大（见图5～7）。

1.4 实验结果分析

图5～7和表2中的实验结果表明：① 平均界面摩擦角为21°～29°；②在所有的实验中，振荡没有缩小的趋势。对于①，可以从块体质量、形状、速度等方面分析影响因素；对于②，需进一步分析界面摩擦的机理。

1.4.1 平均界面摩擦角影响因素分析

以表2所示的试验结果为基础，采用单因素方差分析法分析块体质量、形状、速度对平均界面摩擦角的影响。结果表明，转速的F统计量（均方比）为43.216，对应的P值远小于0.05，满足显著性水平要求；形状F的统计量为0.776，对应的P值为0.473，大于0.05；质量F的统计量为0.647，对应的P值为0.43，大于0.05。故只有转速对平均界面摩擦角有显著性影响，形状、质量的影响不大。考虑到各因素间的相互作用可能对平均界面摩擦角产生影响，因此采用相关系数法，控制2个因素，将另外一个因素对其影响进行偏相关性分析。分析结果如下：设定显著性水平为0.05，当形状与质量作为控制变量时，转速与平均界面摩擦角的偏相关系数为0.957，对应的P值为3×10-5，小于0.05，具有很强的正相关性，故平均界面摩擦角的速率效应明显（见图8）。

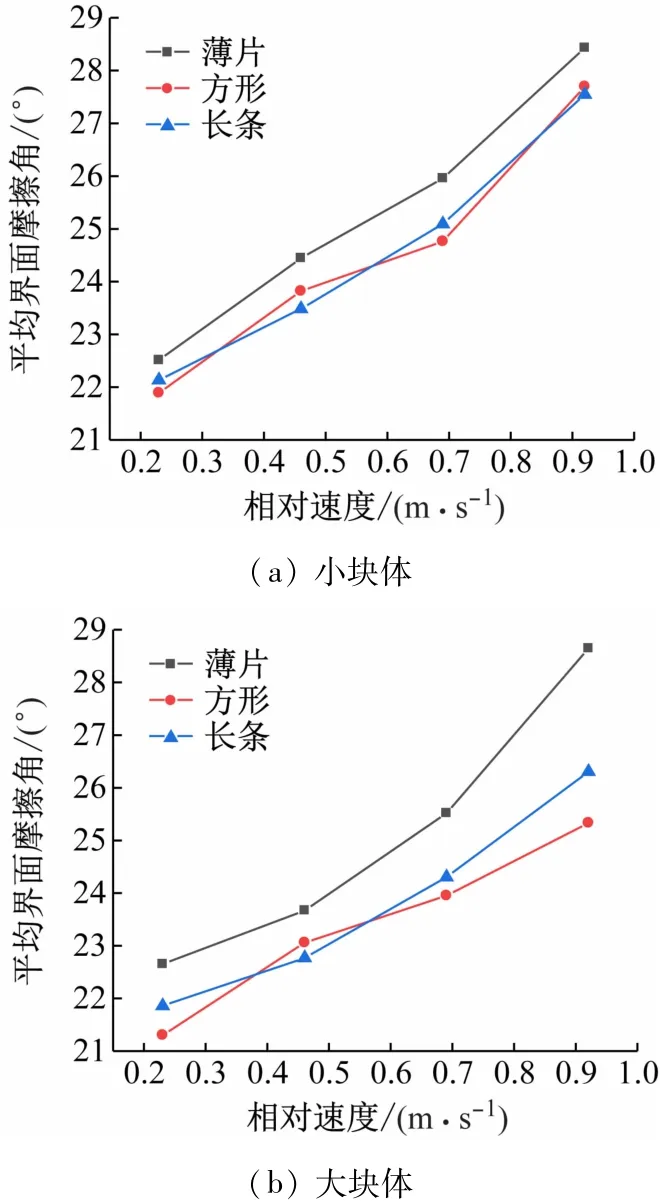
图8 块体相对速度对平均界面摩擦角的影响

1.4.2 振荡机理分析

图4～7表明，块体一直处于振荡运动中，且振荡幅度没有衰减的趋势。可能有两点原因导致了这种振荡运动：①块体的形状不规则，而滚筒的底表面严格来说也是凹凸不平的。这导致两者的相对运动不是稳定不变的，或者说相对运动速度总会受到干扰，从而出现振荡。②设备本身有一定的误差，例如滚筒的旋转总会有一定的偏心，从而导致块体相对于滚筒底表面的相对速度不稳定，引起振荡。为评价设备制造误差对振荡的影响，以大薄片试验结果为例，分析不同相对速度下连续10次往复振荡过程中的运动位置（见图4），发现不同相对速度下的块体振荡除了振幅不一致外，运动周期大致相当，这证明振荡的周期与设备运转的周期相关性不大，因此可以认为大幅度振荡的主要原因不是设备误差。大幅振荡的主要原因可能还是前述第1个原因，即块体的不规则形状和滚筒的不平整表面。这方面的机制调查还需要更多的研究。

2 实验结果的离散元法计算验证

2.1 离散元（DEM）介绍

为进一步验证实测的平均界面摩擦系数（平均界面摩擦角取正切值）可用于数值计算，采用离散单元法［10-11］（Discrete Element Method，DEM）模拟了薄片块体的滚筒实验。考虑到平均界面摩擦系数主要是石英石块体在滑动运动时测得的，因此将平均界面摩擦因数作为DEM的滑动摩擦因数。

在EDEM软件中构造的大薄片状块体多球模型［12］如图9所示，具有132球元、考虑到薄片较薄，因此球半径设为等厚度（1 mm）。计算软件为基于ubuntu系统的开源离散元软件LIGGGHTS。LIGGGHTS计算的理论方程如下，方程中各物理量的具体求解由赫兹接触模型［13］给出，因计算复杂这里不一一罗列。球元对（i，j）法向、切向间接触力及i、j球元受到的转动力矩分别为：

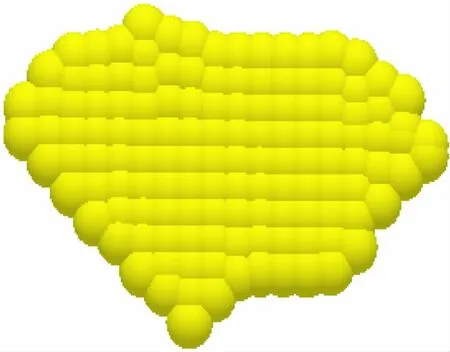
图9 132球元填充的薄片状块体

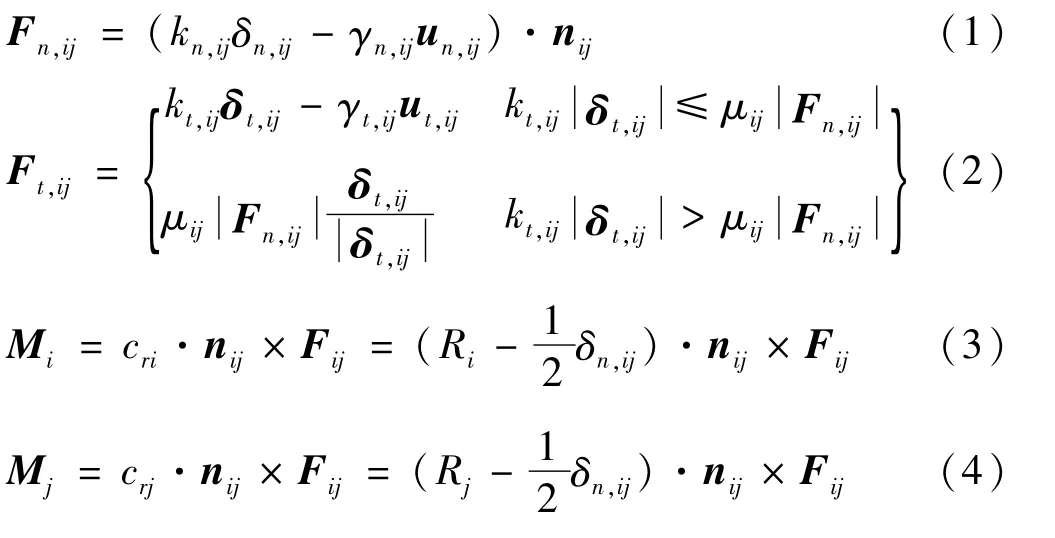
式中：kn，ij和kt，ij分别为球元对的法向、切向弹性系数；γn，ij和γt，ij为球元对法向、切向阻尼系数；δn，ij和un，ij分别为球元对法向重叠量及法向相对速度；δt，ij和ut，ij为球元对切向滑移量及切向相对速度；nij和μi，j为球元对间球心连线的单位法向量及滑动摩擦因数。

在接触模型中，碰撞恢复系数K是一个表征碰撞中能量损失的重要参数，其定义为碰撞后分离速度与碰撞前接近速度的比值［14］，其大小取决于材料物理性质（弹性模量、强度、硬度等）、块体质量、形状、碰撞入射角、入射速度等［15-16］。根据黄润秋等［17］的研究成果，认为对碰撞恢复系数影响最大的是斜坡覆盖层的地质情况，故这里以滚石的启动方式为滑移、坡面覆盖层为基岩裸露、滚石的形状为薄片的因素组合取K值为0.78，数值仿真详细参数如下：模拟域尺寸x∈［-0.03 m，0.03 m］，y∈［-0.145 m，0.145 m］，z∈［-0.145 m，0.145 m］，弹性模量100 MPa，泊松比0.25，碰撞恢复系数0.78，密度2 650 kg/m3，时间步长0.05 ms，模拟时长20 s，滑动摩擦因数：第1组0.439；第2组0.458；第3组0.477；第4组0.507。

2.2 数值计算结果分析与讨论

图10为DEM仿真计算得到的块体瞬时位置与切向速度逐帧统计图。与前述物理实验不同的是DEM块体运动并没有持续的大幅度振荡情况，振幅会随振荡次数的增加而减小，最后趋于零。即块体对应的圆心角趋于稳定，该圆心角可作为界面摩擦角的DEM计算输出结果，块体围绕该界面摩擦角位置做振荡运动直至趋于稳定，且该界面摩擦角附近瞬时切向速度有最大值。

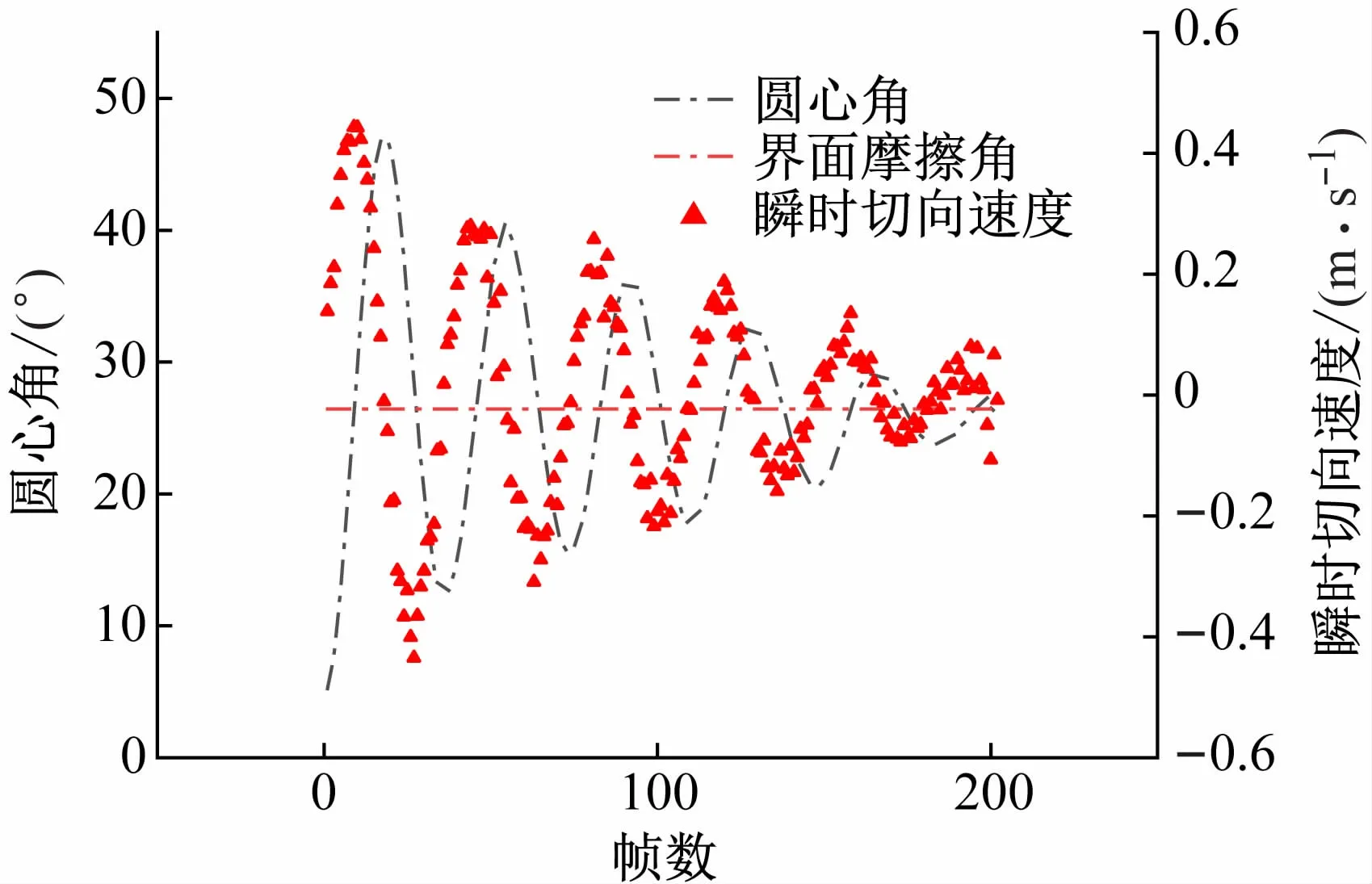
图10 块体瞬时位置与切向速度逐帧统计图

表3总结了所有DEM仿真实验结果得到的界面摩擦因数（DEM界面摩擦角取正切值）和滑动摩擦因数的输入值。两者的差别为1.4%～11.6%，印证了以往研究的结果［2-5］，即DEM计算中的滑动摩擦因数对块体运动的模拟结果具有重大影响。同时，DEM模拟计算结果得到的界面摩擦因数与滚筒实验得到的平均界面摩擦因数（实际是DEM模拟计算的滑动摩擦因数的输入值）接近，说明本研究中采用的DEM方法在模拟平均界面摩擦因数方面是合理的，也验证了滚筒实验实测的平均界面摩擦因数可作为滑动摩擦因数用于DEM模拟计算。

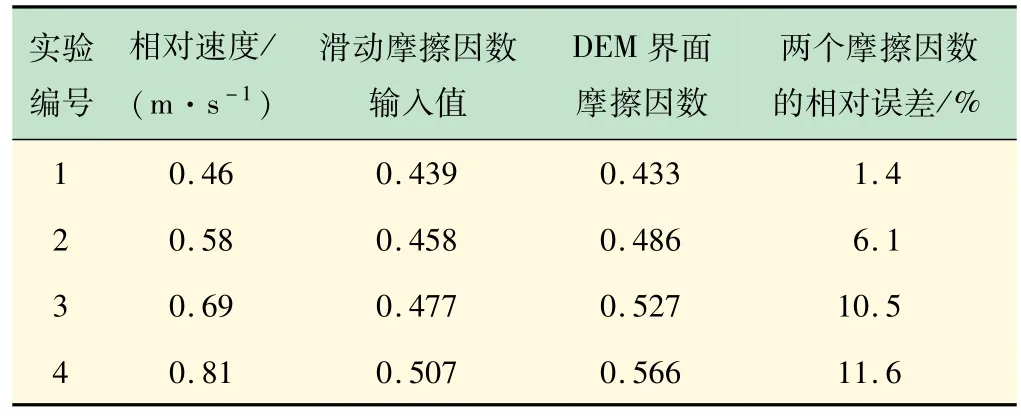
表3 DEM界面摩擦系数统计表（大薄片）

另一方面，图10所示逐帧统计的圆心角θ趋于稳定的运动特征与实际物理实验（见图4）有较大区别，其原因或与本文所用的DEM计算方法和几何模型有关。如前所述，DEM实验排除了设备制造误差带来的持续振荡的可能，因此持续的大幅度振荡或与实际块体底部界面不规则几何特征有关，而多球填充的DEM块体模型（见图9）很难完全模拟实际复杂的界面几何特征，因此持续的振荡不可避免（见图4～7）。本文采用的目前比较常用的DEM计算方法和几何模型在对振荡的仿真方面还不完善，还不能模拟这种持续的大幅度振荡运动。

3 结 语

采用滚筒实验的方法测定了不规则块体的界面摩擦因数。实验中采用动态目标跟踪技术，确定块体在滚筒内运动轨迹的最高与最低点及其所对应的圆心角并将最高点峰值圆心角与最低点谷值圆心角的一半连续振荡20次所得的平均值作为块体的平均界面摩擦角。由于块体底部界面的不规则几何特征等原因，在实验过程中块体出现持续大幅度振荡运动。

采用统计学的分析方法，分析了块体质量、形状、速度对平均界面摩擦角的影响。分析结果表明，质量和形状对平均界面摩擦角的影响不明显，运动速度的影响显著。

采用DEM的方法验证了滚筒实验实测的平均界面摩擦角可用于模拟计算。以物理实验确定的平均界面摩擦角作为数值模拟输入参数，采用开源离散元软件LIGGGHTS验证了实测的平均界面摩擦角可用于数值计算中，同时揭示了目前DEM方法在模拟持续的大振幅振荡现象中的局限性。