斜坡堤护面块体安放过程及稳定性数值模拟

李绍武，王家汉，柳 叶

(天津大学 水利工程仿真与安全国家重点实验室，天津 300350)

抛石防波堤为了抵御巨大的波浪荷载，堤心石外侧往往需要用混凝土块体进行防护，护面块体的稳定性直接决定整个防波堤的稳定性。目前常用的护面块体型式多种多样，例如透空方块、扭工字块体和扭王字块体等。护面块体的外形复杂，体积巨大，安放后各块体间咬合形式也千变万化，这大大增加了护面块体稳定性研究的难度。至今为止，抛石堤护面块体质量仍只能靠经验公式粗略估算，按经验公式确定的护面块体质量一般还需要通过物理模型水槽试验进行检验。在物理模型试验中，护面块体的稳定性与块体的摆放方式密切相关，目前基本靠经验完成，这使得试验结果存在一定主观性。再加上小尺度物理模型试验受比尺效应影响较大，小尺度物理模型的试验结果与实际往往存在偏差。

随着计算机能力的快速提升，数值模拟为块体稳定性研究提供了一种新方法。与物理模型相比，数值模拟方法具有不受比尺效应影响的优势，但目前成果较少。国内外进行护面块体稳定性研究的数值方法主要有网格法、离散单元法、粒子法以及这些方法的相互耦合，如Gotoh等[1]采用DEM-MPS耦合方法，Latham等[2]采用FEM-DEM耦合方法，Ren等[3]采用SPH-DEM耦合法。

目前，护面块体稳定质量的经验公式有Iribarren公式[4]、Iribarren-Hudson公式[5]、Van Der Meer[6]公式等。我国《防波堤设计与施工规范》(后文均简称为规范)[7]也给出了块体质量估算公式。为了揭示护面块体的受力机制，Losada等[8]基于Iribarren数研究了波浪周期和波高对抛石堤稳定性的影响；Jong等[9]考虑了防波堤堤前、堤顶及堤后不同位置处护面块体的稳定性；Leau[10]研究了波浪累积作用对块体稳定性的影响；Altomare等[11]模拟了带槽立方块护面块体的抛石堤在规则波作用下周围的流场变化。

不管是物理模型方法，还是数值模拟方法，亦或是理论分析方法，针对护面块体安放姿态对稳定性的影响，目前研究较少。拟基于DualSPHysics开源代码[12]，开发可模拟现场定点随机安放过程的程序模块；对安放块体进行波浪水槽试验，探讨块体在波浪作用下的稳定性和运动响应，并分析护面块体失稳的典型形式和失稳标准，通过系统化的参数分析，探讨波浪要素及块体安放等因素对块体稳定性的影响。

1 数值模型

1.1 控制方程

波浪运动的质量守恒方程和动量守恒方程的光滑粒子流体动力学(SPH)离散形式为：

(1)

(2)

式中：ρ为粒子密度；t为时间；N为粒子数目；i、j为粒子序号；m为粒子质量；v为粒子速度；W为核函数；P为压强；Γ代表耗散项；g是重力加速度。

DualSPHysics提供了不同的耗散项计算公式，分别用于计算人工黏度[13]、层流黏度[14]与亚粒子尺度(SPS)湍流[15]效应。

1.2 SPH方法

在SPH方法中，利用基于插值函数的积分方程将偏微分形式的连续介质力学质量守恒和动量守恒方程转化为代数方程的形式，从而给出在特定点上流场变量的数值估计。

在SPH中场函数f(x)的积分形式可以由式(3)近似定义：

(3)

式中：f(r)为任意物理量，本质上应该是空间位置矢量r的函数；r、r′为不同粒子的空间位置矢量；W(r-r′,h)称为光滑核函数，h是定义光滑核函数影响区域范围的光滑长度。光滑核函数是影响SPH模型性能的重要参数，这里选用5次样条函数来更好地求解自由表面[16]。

(4)

式中：q=r/h，r是两个给定粒子a和b之间的距离，二维情况下αD=7/4πh2，三维情况下αD=21/16πh3。

在DualSPHysics中，采用了流体弱可压缩假设，流体压力通过状态方程求得[17]，公式为:

P=b[(ρ/ρ0)β-1]

(5)

1.3 固—固接触模拟方法

护面块体间的相互作用属于固体接触问题，现有研究多采用离散单元法(DEM)进行模拟，如Canelas等[18]和Sarfaraz等[19]用SPH-DEM耦合方法模拟了溃坝流作用下立方块体的受力运动。该方法的最大问题是当固体粒子刚度太大时显式积分下，时间步长只能取很小值(通常低于10-8s，而SPH时间步长常为10-5s[18])，影响计算效率，且容易出现数值不稳定问题。Project Chrono法[20]应用时间步进方法，求解描述刚体碰撞、接触和摩擦情况下连续运动的微分变分弱解，大大减少了接触判断工作量，且模型更加稳定；采用完全库伦滑动、黏结及滚动模型，更贴近刚体实际运动过程，控制方程如下：

(6)

式中：r为粒子空间位置矢量;Γ(r)是用来将粒子速度向量表示为粒子坐标向量导数的转换函数;Φ(r)为接触函数，定义如式(7)；v为粒子速度向量；γ为刚度系数；μ为摩擦系数；p为粒子数目；下标n、v1、v2分别表示法向及与法向垂直平面的两个垂直切向方向；D为广义相对位移；fe(t,γ,v)为合外力作用。

(7)

2 块体安放

2.1 安放算法

在工程实际中，防波堤护面块体一般采用GPS定位技术进行定点随机安放。块体安放质量主要取决于吊机操作人员的操作熟练程度和经验。数学模型中块体的安放基本仿照现场施工方法进行块体安放模拟。

Anastasaki等[21]针对Core-Loc护面块体单元的安放开发了数值算法POSITIT/Y3D-R，此算法根据预先确定的块体位置、姿态和走向进行安放，块体的位置主要根据预设的安放密度排算。根据块体的走向，可能出现图1所示的4种安放姿态。

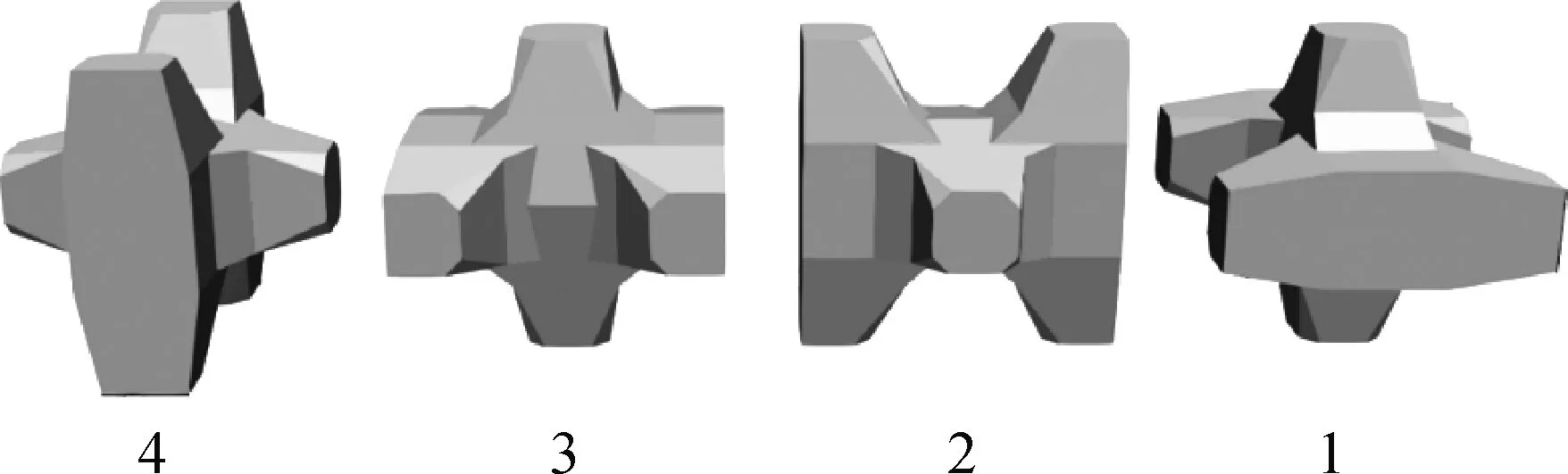
图1 护面块体单元初始安放姿态类型定义

要达到护面块体单元所需的互锁度，完全随机安放和相邻块体安放状态一致都不可取。安放状态既要按一定规则，又需要一定的不规则性。对于菱形布置(图2)，单个块体单元被周围6个块体单元包围，其中与上排及下排各两个块体形成单元互锁；同一行两个单元相邻，但不互锁，却必须具有不同的安放方向。因此，护面块体系统必须具有最少4种不同的单元安放方向(如图1)，才能保证相邻的护面块体单元具有不同的组合。

图2所示的护面块体安放编码系统中，块体单元的安放方向以图1所示4种安放方向类型1，2，3，4为一组，每行块体单元的方向从右往左按照1，2，3，4的序列重复编码。因此每行从左往右第一个块体单元的安放方向确定后，紧接其后连续的3个块体单元的安放方向也随即确定，偶数行第一个块体单元的姿态编号序列从下往上依次为3，2，1，4(如图2自右侧第1列)；奇数行第一个块体单元的姿态编号序列从下往上依次为2，1，4，3(如图2自右侧第2列)。图中同一行相邻块体的水平距离Dh和行与行之间沿坡面距离Dv需根据指定理论堆放密度计算，Anastasaki[22]建议Dh=2Dv。

护面块体安放模块的主要目的就是要保证护面块体按顺序和预定姿态逐个安放到指定初始位置。为此在DualSPHysics模型中加入两个控制变量来控制单个块体的运动。在块体释放之前的一段时间(实际取0.25 s)控制其总力矩为0，其下落速度控制在2 m/s左右(参照Anastasaki等[21]研究设置)；释放后块体按自由落体运动。

2.2 块体参数设置

采用规范[7]推荐的A型扭王字块体，体积为4 m3。根据《混凝土结构设计规范》(GB 50010—2010)[23]，混凝土的弹性模量取为2.80×104N/mm2，混凝土泊松比取0.2。按照Sarfaraz等[19]的研究，混凝土恢复系数取0.55。按照Anastasaki等[21]的研究，块体间摩擦系数取0.55。由于数值模拟中不能模拟实际工程中块体安放过程中的人工扶位，指定的块体安放密度是通过试算不同坡面摩擦系数实现的。坡面摩擦系数取不同的值，块体单元在释放后的自动锁位调整程度不同，具体可以参见Anastasaki等[22]的研究。

定义无量纲块体安放密度PD[22]：

(8)

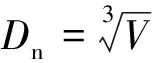
块体初始位置如图3，斜坡堤坡度取为1∶1.5。初始安放参数如表1，其中dx、dy、dz表示初始安放布局时块体中心间距(图3)。

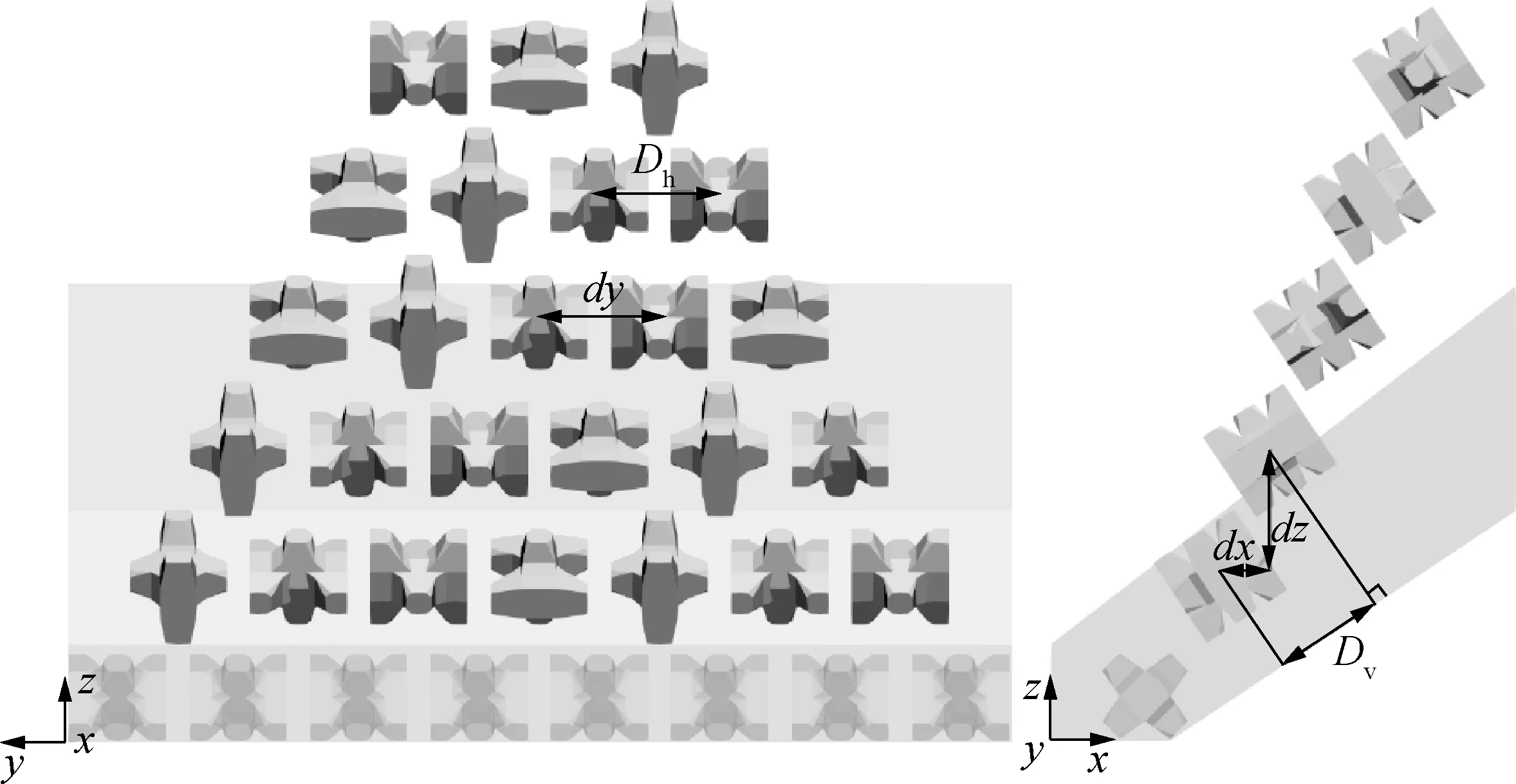
图3 块体初始安放布局

表1 安放参数设置

通过数值试验得到的块体安放密度随摩擦系数变化曲线如图4所示。当坡面摩擦系数等于0.245时，实际堆放密度PD为0.629，其与理论安放密度0.625最接近，误差为0.6%，满足实际堆放密度与理论密度偏差在±5%以内的规范[7]要求。故在块体安放过程中坡面摩擦系数取0.245，而在安放完成后的波浪水槽试验中坡面摩擦系数则仍按照实际取为0.55。

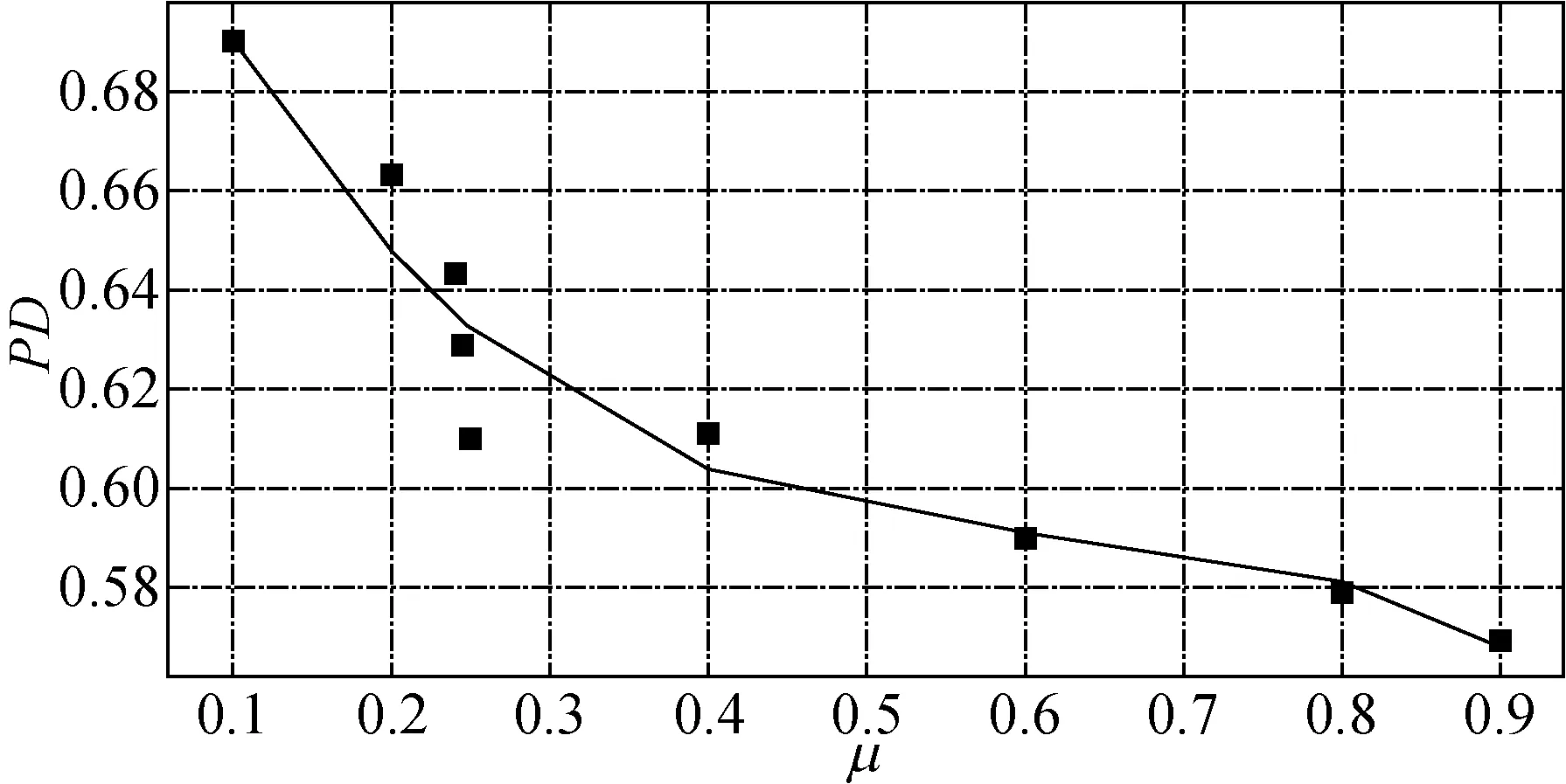
图4 平均无量纲堆放密度随坡面摩擦系数的变化

2.3 块体安放姿态

块体的初始安放姿态与排列次序是影响安放效果的主要因素。如图5所示，共有4种不同初始安放姿态，其中安放姿态O0的鼻轴方向(鼻轴方向定义为穿过两个相同鼻部和块体单元中心，并垂直于包含砧座的平面轴线方向)与全局坐标轴平行，而安放姿态O1、O2、O3，为安放姿态O0同时绕x、y、z轴均顺时针旋转10°，20°，45°的结果。不同初始安放排列如图6所示，其中安放排列次序O4是将初始安放序列中的安放方向类型1和2互换；安放排列次序O5是将初始安放序列中的安放方向类型3和4互换；安放次序O6是将初始安放序列中的安放方向类型1和2互换，安放方向类型3和4互换。

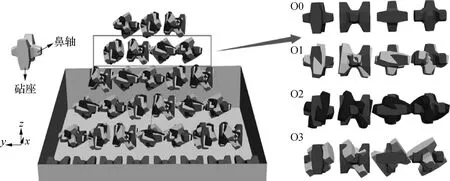
图5 护面块体初始安放姿态

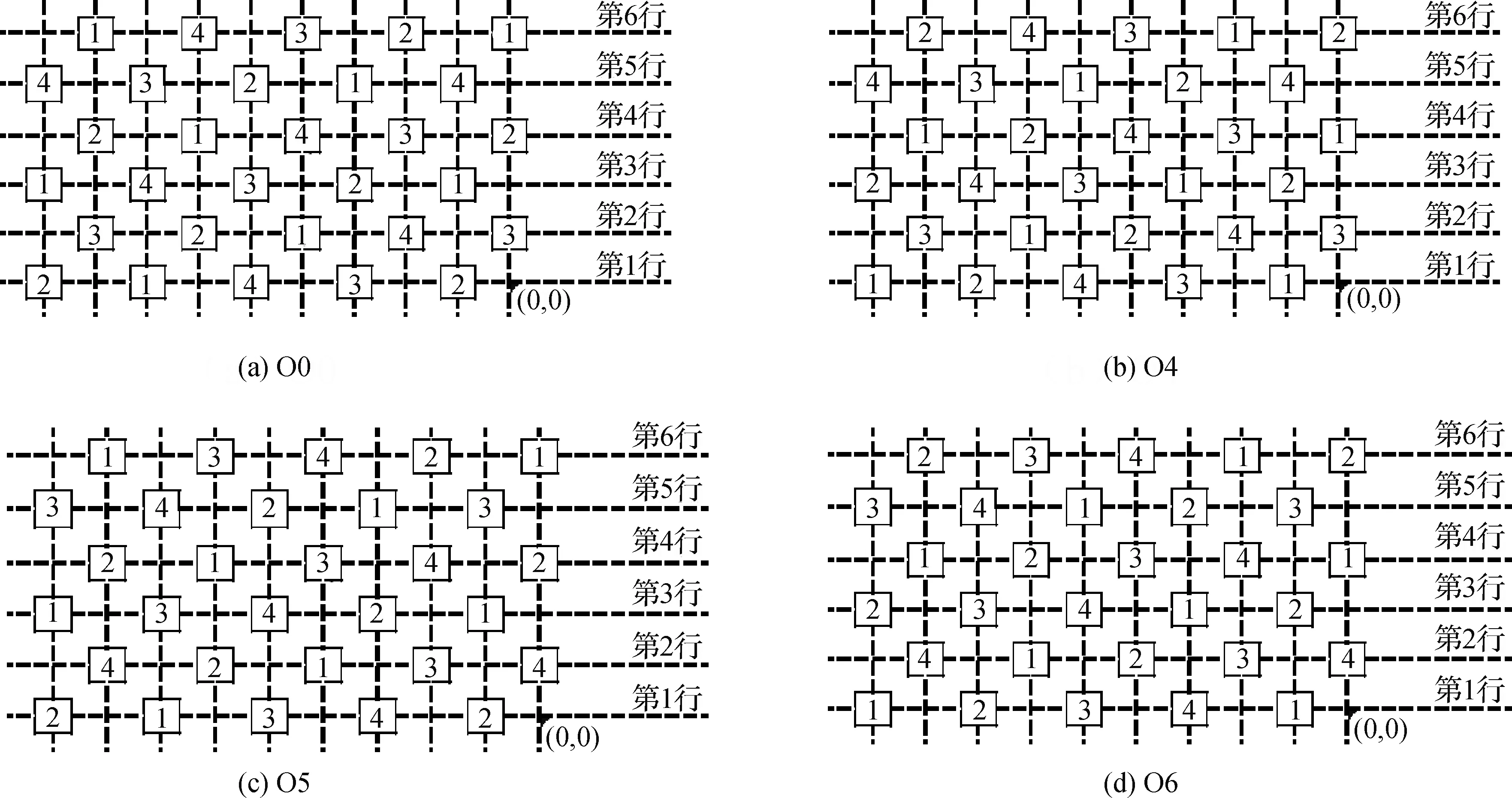
图6 块体初始安放方向排列次序

表2中的数值试验结果表明，不同安放姿态和排列次序对安放密度均有影响，但后者影响更为显著。检查护面块体轴线(鼻轴线)方向分布是否合理的方法是采用赤平投影法[25]，Latham等[26]将该方法运用于Core-Loc护面块体层。扭王字块体具有三轴对称的特点，可以唯一地绘制鼻轴方向，通过鼻轴方向的分布可以简单地表征块体安放方向的分布。用赤平投影图表示鼻轴方向的分布，将坡面设为鼻轴赤平投影图中赤道坐标系所在平面，同时将沿坡面上、下坡方向分别设为N-S(s轴方向)方向，沿防波堤堤干方向为W-E方向(y轴方向)。块体鼻轴方向的走向角和仰俯角可以从数值模拟结果提取。

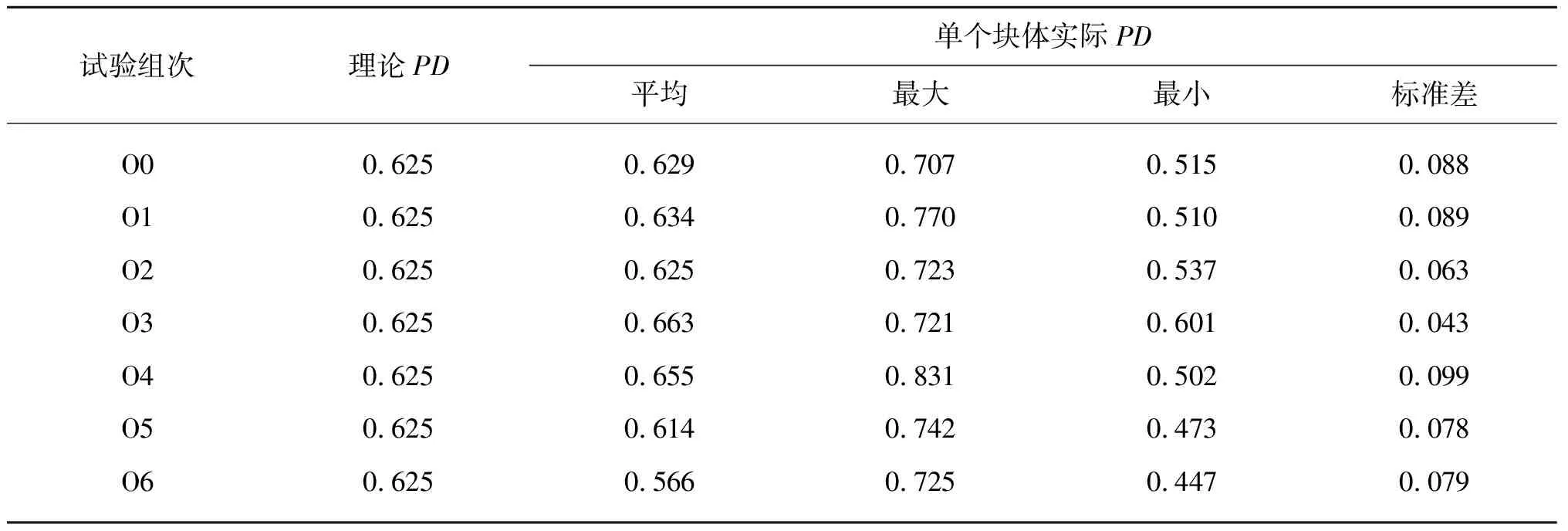
表2 单个块体无量纲安放密度

图7为不同安放姿态及次序下的块体鼻轴方向赤平投影分布，其中大黑点表征块体初始安放姿态时的鼻轴方向，小黑点表征块体安放完成后的鼻轴方向。由图7可知，安放完成后扭王字护面块体鼻轴方向的分布与初始安放姿态密切相关，而与初始排列次序关系不大，随着初始安放姿态鼻轴方向逐渐接近，安放完成后的鼻轴方向分布也逐渐集中。

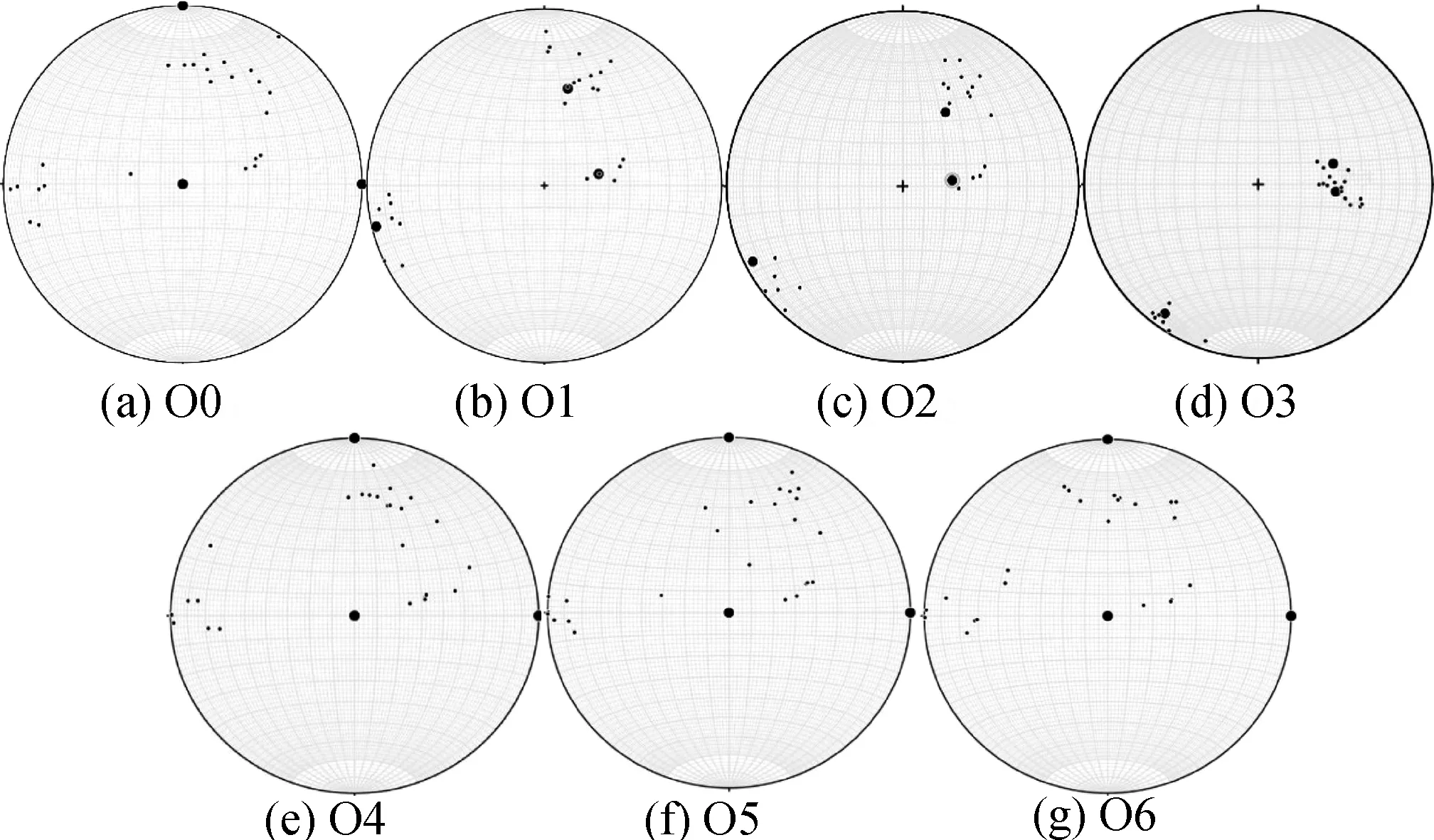
图7 块体鼻轴方向赤平投影

3 块体稳定性

护面块体失稳有滑移失稳、滚动失稳和上举脱出失稳3种形式[27]，影响其稳定性的因素也多种多样，并且失稳状况与采用的失稳标准有密切关系。因而研究不同失稳判别标准和不同影响因素下块体的失稳状况及失稳模式是必要的。

3.1 模型设置

模型试验的设置参照钟雄华等[28]的物理模型试验，按照块体尺寸比例还原为原型尺度，块体体积为4 m3。数值模型试验设置如图8所示，水槽宽度14.65 m。研究中波浪采用推板式主动吸收造波系统造出的二阶规则波。因水深较大，只在静水面一个波高范围内设置扭王字块体，高度范围6.75 m，理论安放密度为0.625，坡面中部设肩台用以支撑护面块体，肩台高度为13.928 m。

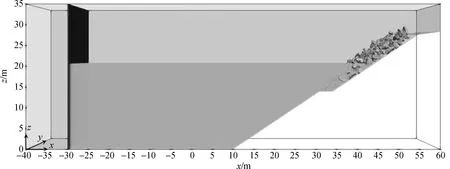
图8 三维数值水槽模型

以下针对波浪条件(波高H、波周期T)、块体安放姿态及排列次序(O)、坡面坡度(1∶m)以及块体缺位(S)的影响进行讨论。块体缺位如图9所示，块体初始安放姿态O7是将O0中所有块体安放方向均设置为方向类型2(如图1)的结果。坡面摩擦系数(μf)和块体摩擦系数(μ)均取为0.55，模型参数设置如表3，工况设置如表4，其中dp表示模型中粒子间距。

图9 块体缺失空位

表3 模型参数设定

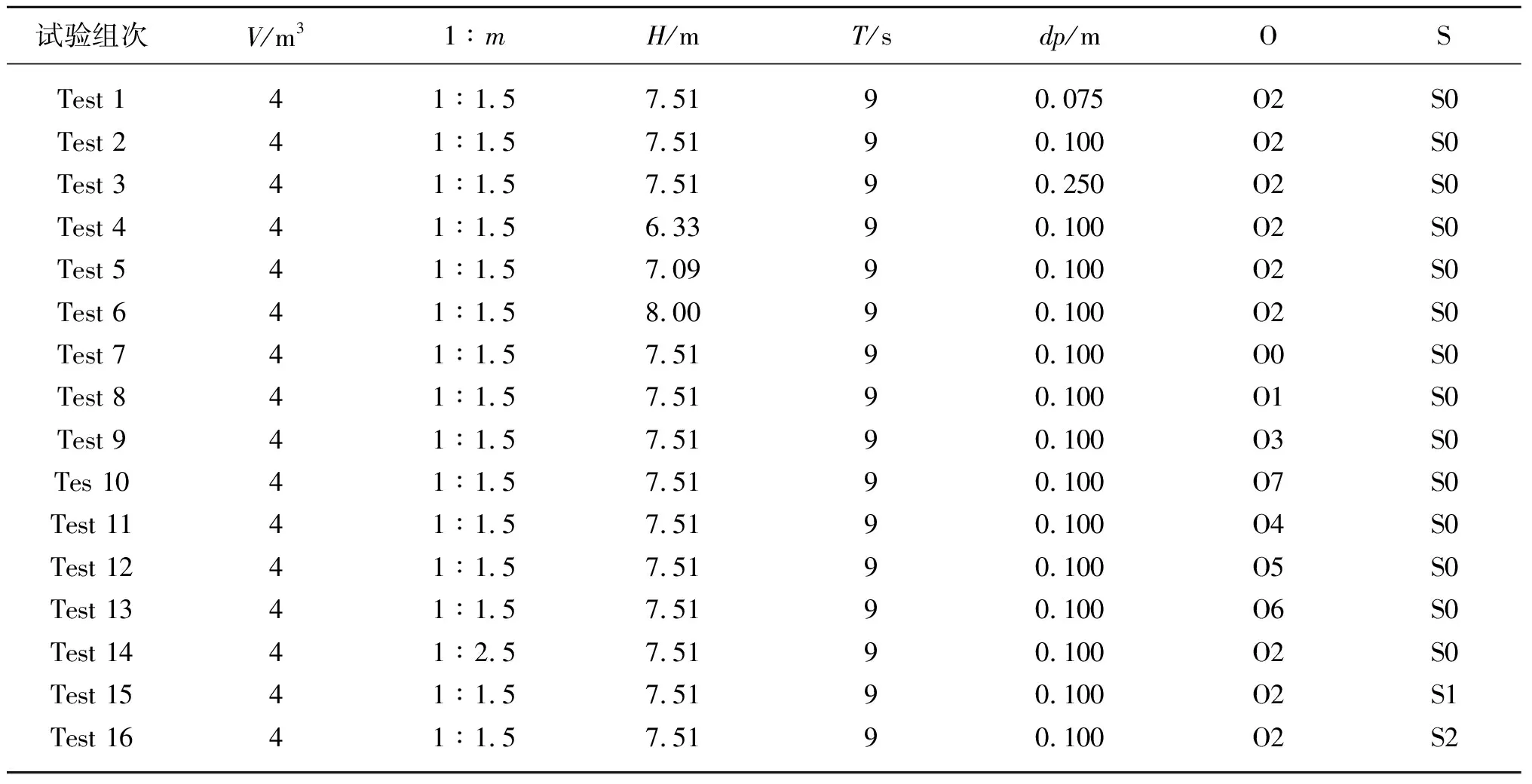
表4 数值模拟试验工况设置

3.2 稳定性参数

1)块体相对破坏水平Nod

工程上，块体失稳标准一般由指定宽度DB内超过限定位移量的块体个数Nod来判断[29]。

(9)

式中：Ndisplaced为块体失稳个数，B为水槽宽度，DB为单个块体水槽宽度方向的等效尺寸。

根据《波浪模型试验规程》(JTJ/T234—2001)[30]，块体中心位置累积位移超过块体最大几何尺度一半(0.5DH)时即认为失稳，即D/DH<0.5时块体稳定，其中D是护面块体单元中心位置在外力干扰下的位移,单位为m。

2)块体稳定数Ns

Hudson等[31]提出的经验稳定参数Ns定义为:

(10)

式中：Hs为有效波高；Δ=ρa/ρwater-1为块体相对密度，ρa为块体密度，ρwater为水体密度。

3)安全位移比SDP

Anastasaki等[21]提出安全位移比(safe displacement percentage，简称SDP)来衡量护面块体在外力作用下的稳定性。

(11)

式中：Nsafe为处于安全位移范围内的块体数目，N是护面块体总数目。Anastasaki等[21]在研究中以D/Dn<0.3为块体的安全位移范围标准，文中研究同样采用此判断标准。

4)稳定性系数KD

当采用Hudson公式或我国防波堤工程规范的块体稳定质量计算公式时，可以用稳定性系数KD来度量块体稳定性。KD值大小表示块体在护面层中稳定程度,一般由式(12)确定。

(12)

式中：Hs为入射波的有效波高。

KD值随稳定标准及失稳率取值不同也不同，破碎波情况下扭王字护面块体一般取10～12[32]，非破碎波情况下CLI[24]建议取15。

3.3 粒子尺度敏感性分析

粒子尺度既影响模型的分辨率和计算精度，又影响计算量。分别用0.075 m，0.100 m和0.250 m三种粒子尺度参数进行敏感性分析，结果如表5所示。可以看出，采用0.250 m的粒子尺度得到的块体失稳个数与另外两组相差较大，而采用0.100 m的粒子尺度得到的块体失稳个数与0.075 m的结果相差很小，说明0.100 m 的粒子尺度基本收敛，考虑计算时间，确定粒子尺度取0.100 m。

表5 不同粒子间距下块体稳定性参数统计

3.4 块体运动和受力分析

以Test 2为例，分析波浪作用下块体的运动响应及受力特性。图10为Test 2下护面块体层中位移最大的扭王字块体单元(记为块体A，位于护面块体层中部偏上位置)在波浪力作用下的中心位置三个坐标随时间变化。从13 s开始，第一个波浪作用后，块体A在波浪的冲击作用下先发生了沿坡面向上(x、z方向)运动，而后在波峰过去后随即发生了相当大的沿坡面向下的位移；与此同时，沿堤干方向(y方向)也发生了较大的位移运动，这说明在第一个波作用下块体即发生了失稳运动。第二到第四个波作用下位移相对较小，每个波作用后块体A的位移运动趋势与第一个波相同。可见在大波作用下，扭王字护面块体层在较短的时间内就发生了失稳。而在此工况下，护面块体层整体发生的是滑移失稳。

图10 波浪作用下块体单元中心位置坐标随时间变化

图11为一个波浪周期内块体单元所受流体力的变化。从图11中可以看出当波峰作用时(t=13 s、t=22 s)，护面块体层主要受波浪爬坡的冲击作用，护面块体层表面为受力集中区，此时护面块体层所受的波浪力最大，峰值为8 000 N左右，注意这里所受波浪力是指块体单元粒子化后单个粒子受力状况；当波谷作用时(t=16 s、t=19 s)，护面块体层主要受波浪回落的向下作用力，块体层底部为受力集中区且波浪力较小。护面块体单元空间受力不均匀导致块体内部出现应力集中区，是导致块体滑移、跳脱和翻滚的重要因素。

图11 一个波周期内块体所受波浪作用力

3.5 块体稳定性影响因素分析

首先计算各工况下块体最大位移，并据此判断块体是否失稳及统计失稳个数，进而对3.1节介绍的稳定性参数进行计算，结果如下。

1)由图12可知，随着波高的增大，块体整体下滑趋势逐渐增大，同时也出现了单个块体脱离护面块体层的趋势。由表6可以得出，块体失稳临界波高在7.09～7.51 m之间。由这个波高，根据式(12)可以反推出临界KD值的取值范围为21.64～26.20，而规范推荐值为15，规范推荐值一般会预留一定安全系数(一般取1.5[33])。进一步计算得到块体失稳的临界稳定性系数Ns在3.19～3.40之间，该值约为设计推荐值2.5的1.3倍。在波高7.09～7.51 m之间，块体层发生临界失稳(Nod=0)和整体失稳破坏(Nod>0.5[33])，对应稳定性系数Ns位于3.19～3.40之间。这意味着在大波高情况下，扭王字块是稳定的，但一旦稳定性破坏开始后，结构将逐渐失效，说明了安全参数取值的必要性。

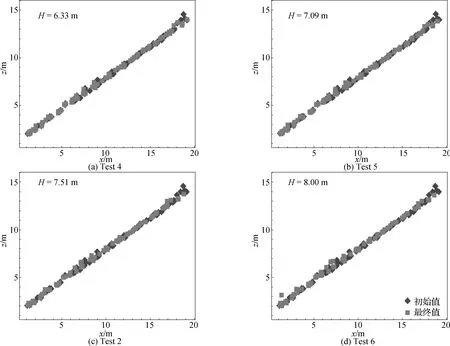
图12 不同波高作用下块体波浪作用前后中心位置变化

表6 不同波高作用下块体稳定性参数统计

2)对块体安放初始姿态及排列次序的试验结果(表7)表明，块体初始安放姿态和排列次序对稳定性均有较大影响。

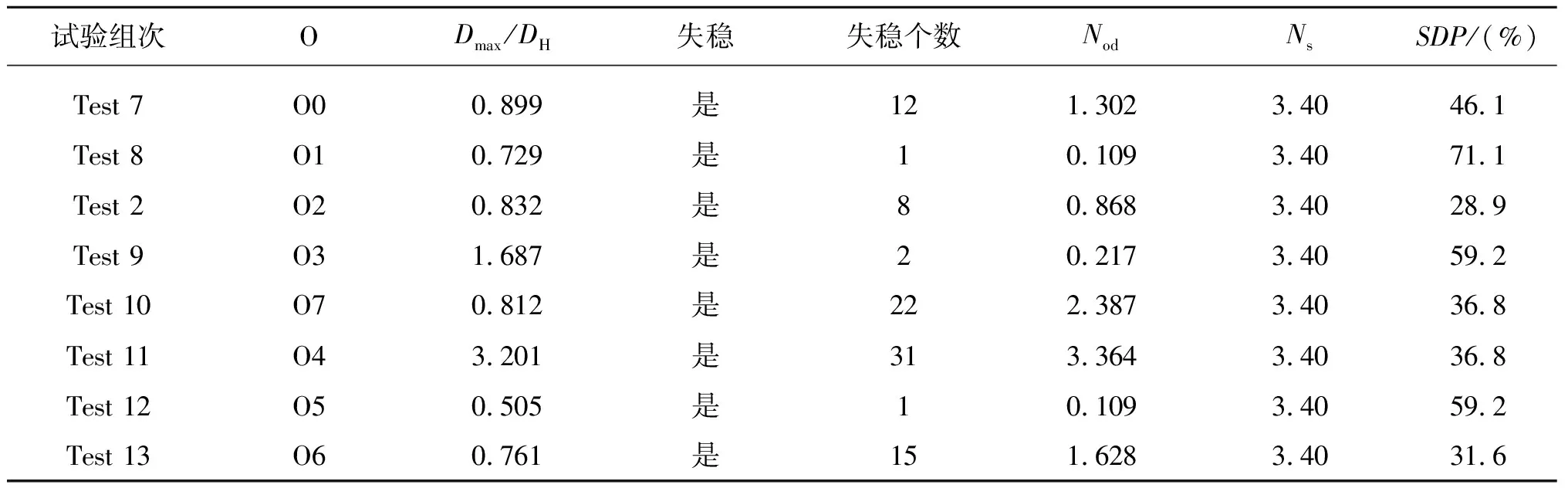
表7 不同初始安放布局下块体稳定性参数统计

由2.3节安放初始排列次序对块体安放完成后鼻轴方向的分布影响不大可知，块体安放完成后鼻轴方向的相对位置也对块体稳定性有所影响，且主要影响单个块体的上举脱出失稳(图13)。而从表7和图14可以看出，波浪作用前鼻轴方向赤平投影图越分散，块体在波浪作用下越稳定，这是因为扭王字护面块体的特点就是形状复杂，依靠块体之间的高度互锁来提高稳定性，而波浪作用前块体鼻轴方向赤平投影越分散，块体之间的互锁程度越高。

图13 不同初始安放次序下块体波浪作用前后中心位置变化

图14 不同初始安放姿态下块体波浪作用前鼻轴方向赤平投影

3)在坡度为1∶2.5下，并未出现护面块体层的整体下滑，仅顶部少量块体出现了下滑。相比坡度为1∶1.5而言，同等条件下，坡度为1∶2.5下护面块体层在波浪前进方向的投影面积更小，因此坡度为1∶2.5下，所受波浪力更小，故更为稳定。同时坡度变缓的情况下，护面块体之间的支撑作用减弱，坡面对块体的支撑作用增强，而块体之间互锁摩擦作用增强，坡面摩擦作用减弱。因此在波浪作用下不易出现整体下滑运动，但扭王字护面块体之间的互锁优势可能减弱，因为支撑作用的减弱会导致块体之间的接触力变小，护面块体更容易从护面块体层脱落(图15圆圈标示处块体)，从图15可以看出这种趋势，这与钟雄华等[28]的物模试验结果结论相近。

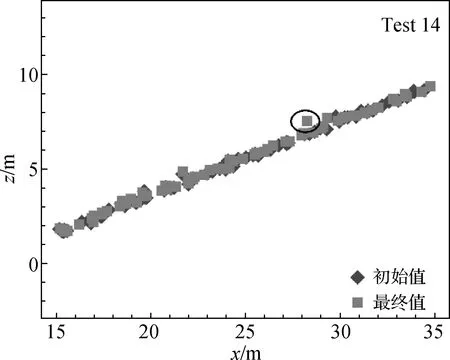
图15 坡度为1∶2.5下块体波浪作用前后中心位置变化

4)不同位置块体的缺失对护面块体层稳定性也有影响。试验表明在波浪作用下块体的缺位会得到其上侧块体的自动补位(图16)。但这种补位造成了周围块体互锁效果的减弱，从而容易导致缺位周围的块体上举脱出失稳(图17)。

图16 不同位置块体缺失下块体波浪作用前后中心位置坡面投影坐标

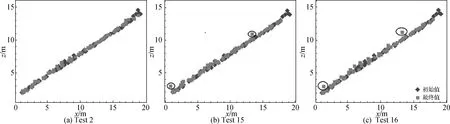
图17 不同位置块体缺失下块体波浪作用前后中心位置变化

4 结 语

基于DualSPHysics数值模型对斜坡式防波堤上扭王字护面块体的安放过程及波浪作用下的稳定性进行了三维数值模拟，主要结论如下：

1)在块体安放过程中，通过摩擦系数试算，可以实现按安放密度进行块体安放。

2)对块体安放姿态和安放排列次序对安放效果的影响研究表明，不同安放姿态和安放排列次序对实际安放密度的实现均有影响，但后者影响更为显著。

3)由不同波高的试验表明，扭王字块体KD值的取值范围为21.64～26.20，是规范推荐值的1.5倍左右，且块体临界破坏和完全失效时的Ns非常接近。

4)波浪作用前块体鼻轴方向在坡面上的赤平投影越分散，块体越稳定；鼻轴方向的相对位置主要影响单个块体的上举脱出失稳；坡面坡度变缓的情况下，护面块体层整体下滑趋势减弱，但更易发生上举脱出失稳；单个块体缺失情况下块体的缺失位置会导致缺失块体周围的块体上举失稳。