隧洞块体破坏过程及稳定评价的数值方法研究

陈世杰 ，肖明 †，陈俊涛

（1.武汉大学水资源与水电工程科学国家重点实验室，湖北武汉430072；2.武汉大学 水工岩石力学教育部重点实验室，湖北武汉430072）

在隧洞施工过程中，不可避免地遇到岩体内复杂的地质结构面，例如断层、裂隙、剪切带和节理等．这些结构面造成岩体内部的不连续性，易形成块体并发生局部塌方[1]．因此研究隧洞块体的破坏过程及稳定性对保证工程安全具有重要意义．

针对块体的稳定性分析，Goodman和Shi[2]提出了关键块体理论，并用刚体极限平衡法计算块体安全系数．基于块体理论的软件如GeneralBlock[3]和Unwedge[4]等广泛应用于地下结构的块体识别和稳定性评价中.这些方法把块体运动类型分为脱落、单面滑动及双面滑动，将块体看作脱离体，仅考虑块体自重和滑动面作用力下的极限平衡.在浅埋块体中，刚体极限平衡法是合理的.但对于深埋块体，其复杂围岩的开挖卸荷作用对块体稳定性有重要影响[5].王思敬等[6]、黄润秋等[7]研究了考虑地应力影响的块体稳定性，采用有限元方法计算块体所在部位的围岩应力状态并投影到块体滑移面上，进而求解块体安全系数.但其将围岩变形和块体稳定分开计算，不能较好反映实际情况下的围岩对块体的作用力.对于复杂围岩条件，块体在破坏过程中受到围岩变形和多个结构面应力的影响，如果忽视了围岩与块体的相互作用，将导致稳定性评估的偏差，并可能增加块体的支护代价[8].以上常用的块体稳定性分析方法忽视了围岩应力和变形的影响，更不能反映块体的破坏过程．

在数值方法上，巨能攀等[9-10]基于非连续分析方法，利用离散单元法计算块体之间的相互作用，分析块体的变形和破坏过程，并利用极限平衡理论计算块体安全系数.该方法较多应用在边坡块体稳定性问题，而基于连续介质的分析方法在地下工程中已经十分成熟，能有效考虑地应力、开挖卸荷和围岩变形特性.张雨霆等[11]提出单元重构的断层建模方法，可实现基于网格的块体识别，将连续介质数值分析方法引入到块体稳定问题.张雨霆等进一步引入界面单元，并基于FLAC3D提出岩石块体稳定性评价的一般性方法[12].虽然非连续分析方法可反映块体的破坏过程，但连续分析方法对块体的围岩计算效果更佳.现有块体稳定分析的数值方法还不能很好结合非连续和连续分析方法的优势.以上分析思路为本文研究提供了有益借鉴．

针对现有块体稳定分析中的不足，本文提出了一种基于连续介质力学的块体破坏数值分析方法，可同时模拟围岩的变形特性和块体的破坏过程.首先在已有的单元重构-节点分离的结构面建模方法基础上，介绍基于网格的块体识别方法.然后引入显式求解的接触力算法[13-14]，提出块体和围岩的接触分析方法.该数值方法在网格模型中考虑了点对、点面接触类型，可模拟块体与围岩发生粘结、滑移和分离3种接触状态.最后，基于结构面强度折减法，计算块体的安全系数.结合某一断层穿过的隧洞工程，分析块体和围岩的稳定性.研究结果可为复杂地质条件下的隧洞块体稳定性提供有效的分析思路．

1 基于网格的块体识别

隧洞开挖过程中，暴露在临空面上的失稳块体称为关键块体.其失稳破坏后，可能产生连锁反应并造成整个洞室塌方[2].发生连锁反应的块体为潜在危险块体，大方量的潜在危险块体增加了洞室的施工风险，因此，数值计算前的块体识别十分重要.它需要建立包含复杂地质结构面信息的网格模型，并通过搜索来标记可动块体.以一个简单的二维模型为例，基于网格的块体识别方法主要步骤如下：

1）建立不考虑地质结构面的网格模型.如图1（a）的初始网格有4个单元．

2）获取结构面的空间几何参数，包括产状、间距、长度等.采用单元重构的结构面建模技术对网格单元进行二次划分，通过局部调整和添加单元内辅助线来保证单元类型的规则化[11].如图1（b）中模型被两条结构面切割并重构成13个单元

3）采用节点分离技术[15]，将块体单元与围岩单元的共用节点进行分离，模拟结构面两侧的非连续特性，并得到初始接触对，如图1（c）所示．

4）检查单元的几何形态.通过计算雅克比矩阵和单元体积等剔除无效节点和单元．

5）标记可动块体.互相交叉的结构面将模型划分为多个区域，将同一区域的单元进行聚合形成块体，综合开挖面、模型边界等进一步识别危险的可动块体.如图1（d）中的模型标记出4个块体．

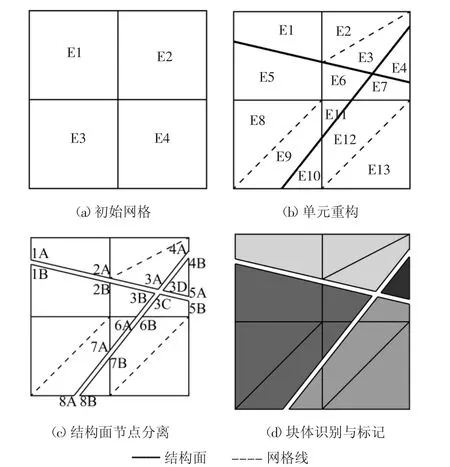
图1 块体识别简单示例Fig.1 Simple example of block identification

以上内容为数值分析的前处理部分，可通过自编程序实现对二维和三维的自动化处理，有效得到含标记块体的网格模型．该块体识别方法不同于传统块体理论，可有效标记洞周所有关键块体和潜在危险块体.而且由于标记的块体由单元组成，可将其引入数值计算来分析块体的破坏过程及稳定性．

2 块体和围岩的接触分析方法

块体在破坏过程中与围岩存在复杂的相互作用.由于开挖卸荷作用，块体可能发生脱开和滑移.关键块体的脱落也给潜在的危险块体提供新的临空面，引起局部塌方.本文基于显式积分算法，考虑块体与围岩的多种接触类型，建立块体与围岩的接触分析方法．

2.1 接触系统的显示有限元积分格式

块体不仅受到自身初始应力、其他各类点、线、面和体荷载，还受到惯性力、阻尼力以及接触力的作用.经过有限元离散后，块体和围岩在考虑接触力后的节点运动微分方程可表示为：

对节点的加速度采用中心差分法进行求解，即

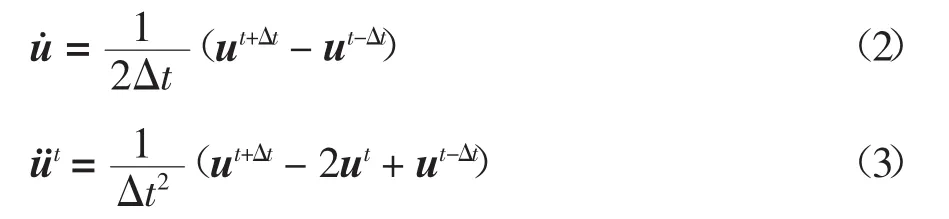
将式（2）（3）代入式（1），转换后可得到t+Δt时刻的节点位移表达式：

式中：t为时间；Δt为时间步长；ut+Δt为该时刻节点位移向量为不考虑接触力向量的节点位移向量；Δut+Δt为由接触力引起的附加位移场向量．

从上述有限元积分格式可看出，t+Δt时刻的块体运动状态可由t和t-Δt时刻的运动状态以及接触力求出．而只有接触力Rt是未知的，需要根据t～t+Δt时刻的接触状态进行判断并计算．

2.2 多种接触类型的接触力求解

在块体识别过程中已建立块体与围岩的初始接触对.在岩体未扰动之前，认为围岩与块体的接触面胶结良好，初始接触类型为点对接触.发生滑动之后，块体与围岩发生滑动和分离，此时，接触节点与其对应单元某一面接触，称为点面接触.图2分别为点对接触类型和点面接触类型的示意图.块体与围岩在其接触面上可发生粘结、滑动和分离3种接触状态.下面推导多种接触状态下的接触力计算方法.

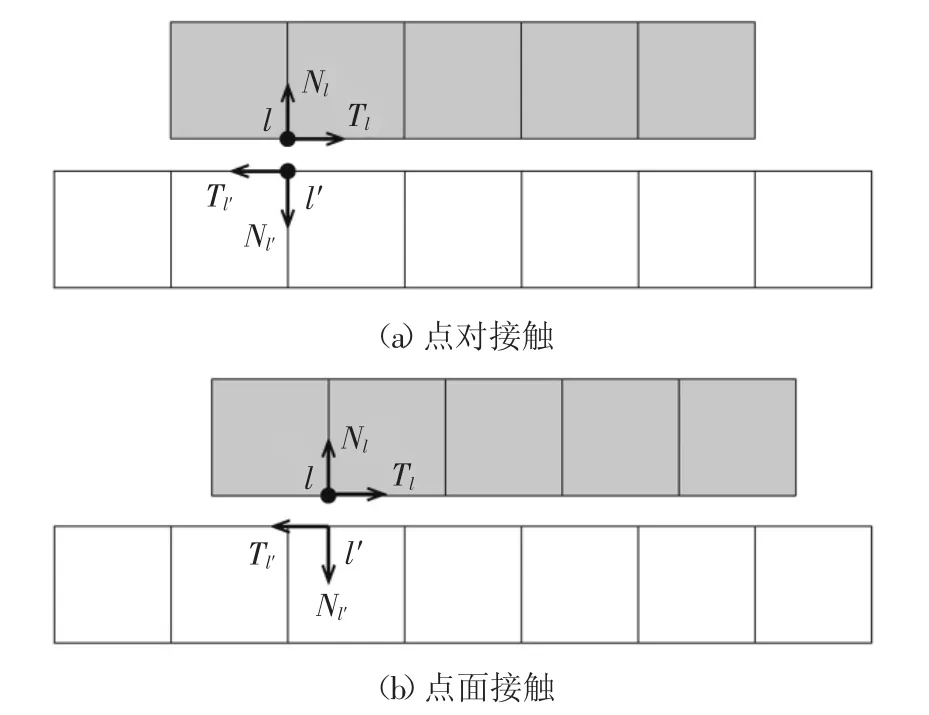
图2 块体与围岩的接触类型示意图Fig.2 Sketch of contact types between block and rock

2.2.1 点对接触类型

假设t+Δt时刻接触节点对l和l′处于粘结接触状态（图2（a）），则该接触点对需满足法向互不嵌入和切向无相对滑动条件，即：

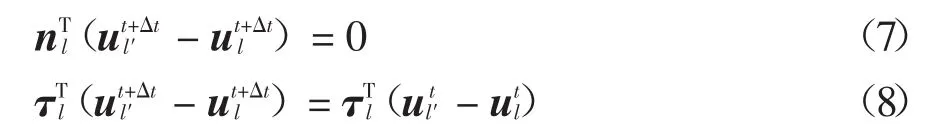
式中：nl为接触点对的单位法向矢量，从l′指向l；τl是对应的单位切向矢量.

联立式（4）～式（8），并根据 Rt=Nt+Tt和可得到：

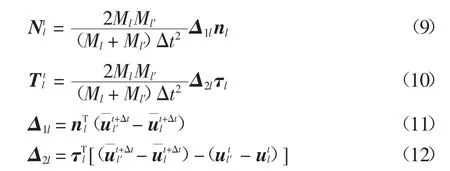
式中：Δ1l和Δ2l表示不考虑接触力向量下接触点对的相对法向和切向位移；Ml和Ml′分别为节点l和l′的集中质量.的法向和切向分量

以上接触力大小是在假定粘结接触状态下推导得到的.但在块体的破坏过程中，接触点对还可能发生滑动或分离.因此，每一时间步计算完成后，需对满足以下条件的接触点对的状态和接触力进行修正.

若Δ1l＞0，表明接触点对有互相嵌入的趋势，接触状态可能为粘结或滑动.进一步比较其切向接触力大小与结构面抗剪强度的关系，若+cA，说明接触点对发生滑动，此时的接触力修正如下：

若Δ1l＜0，表明接触点对有互相分开的趋势，接触状态可能为粘结或分离.进一步比较其接触力大小与粘聚力的关系,说明接触点对突破粘聚力，并发生分离，此时的接触力修正如下：

式中：μs、μd分别为静和动摩擦系数；A为计算接触点对的控制面积；c为接触面的粘聚力.若在t+Δt时刻之前接触节点未发生滑动或分离，则c＞0.若在t+Δt时刻之前接触节点已突破粘聚力，则c=0.

2.2.2 点面接触类型

块体在上一时间步中发生较大相对滑动，使接触节点l处于点面接触类型.假设t+Δt时刻节点l与某单元面处于粘结接触状态，记单元面上的接触点 l′与节点 l对应（图 2（b））.l′在 t时刻的位移、等效集中质量，可通过有限元形函数插值计算得到：

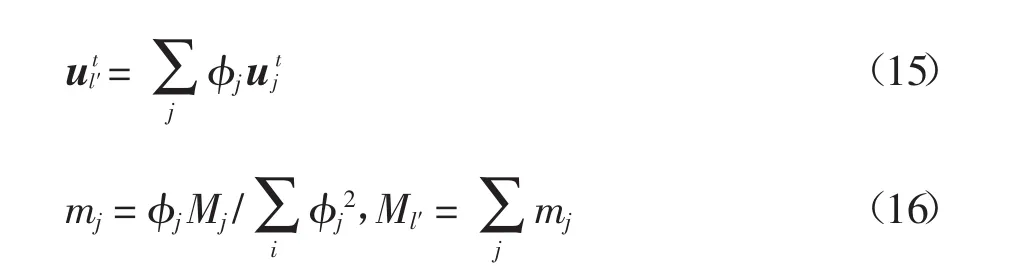
式中：j为l′所在单元的节点；φj为节点j的形函数在接触点l′处的值；Mj为节点j的集中质量；mj为节点j在接触点l′的质量贡献.

每一时步计算完之后同样需要对接触状态和接触力进行修正.点面接触类型下粘聚力c=0，因此其接触面上的抗拉力为零，抗剪强度为

2.3 接触分析方法的基本步骤

隧洞开挖之前，接触面上的节点均为粘结的点对接触.隧洞开挖之后，当块体的接触点对突破粘聚力发生滑动后，需要通过接触搜索确定接触类型，根据块体与围岩的接触分析方法计算每一时步的变形特性.该分析方法不需要确定弹簧刚度，且发挥了显式求解的高效率和稳定性优势，模拟了块体与围岩的非连续变形特性.对于t+Δt时刻块体与围岩变形状态的的计算流程如图3所示.

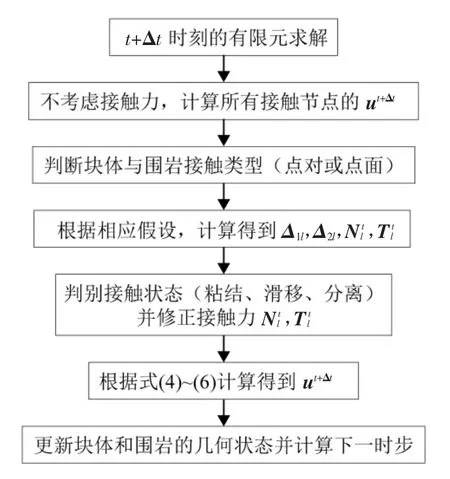
图3 计算流程Fig.3 Flow chart of contact analysis

3 块体安全系数求解方法

采用结构面强度折减法来定量评价块体的稳定性.结构面作为块体和围岩的非连续接触面，其力学性质对块体的抗滑稳定十分重要.由于结构面主要发生剪切破坏，主要考虑其粘聚力c和摩擦角φ的影响.不同的抗剪强度参数产生不同的接触力矢量R，并影响块体的稳定性.因此对结构面的强度参数进行同步折减可求出块体的临界失稳状态，即

式中：Fs为强度折减系数；c和c′分别为强度折减前后的粘聚力；φ和φ′分别为折减前后的内摩擦角．

首次计算时不考虑强度折减，即Fs=1．对于稳定块体，在有限步以内，块体和围岩完成变形协调，达到平衡状态，即认为折减系数Fs在[1，+∞]之间．否则，认为该块体不稳定，其折减系数在[0，1）之间．Fs在相应区间内，不断增大，直到发生临界失稳，此时的折减系数认为是块体的安全系数．计算中以特征点的位移突变作为临界状态的判据[16]．

对于顶拱冒落块体，其安全系数无限接近于零；对于倒楔形的不可动块体，其安全系数接近于无穷大．计算中认为Fs小于0.1即发生块体自由脱落，Fs大于100即为不可动块体．

4 算例验证

采用Fortran语言将上述块体和围岩接触分析方法嵌入自主研发的显式有限元计算框架中，形成块体破坏数值计算程序．

为验证块体和围岩接触算法以及安全系数求解方法的计算精度和合理性，选择一个块体沿双面滑动破坏的算例，并与解析解进行比较．如图4所示，一尺寸为2 m×2 m×2 m的方块被△ABC和△ADC两个面切割，形成可沿双面滑动的块体．滑块和斜坡均为线弹性体．两者的弹性模量为20 MPa，泊松比为0.3，密度为2 000 kg/m3．模型底部固定，块体受自重情况下自由沿双面滑动．块体在运动初期的理论位移可表示为[17]：

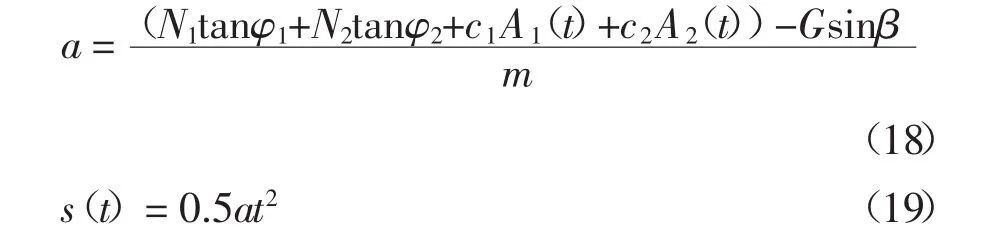
式中：a 为块体的加速度；s（t）为块体的位移；t为时间；N1、A1、φ1、c1分别为滑面△ABC 的法向力、接触面积、摩擦角和粘聚力；N2、A2、φ2、c2分别为滑面△ADC的法向力、接触面积、摩擦角和粘聚力；G为块体自重；m为块体质量；β为滑动方向的倾角；G=mg，取g=10 N/kg．

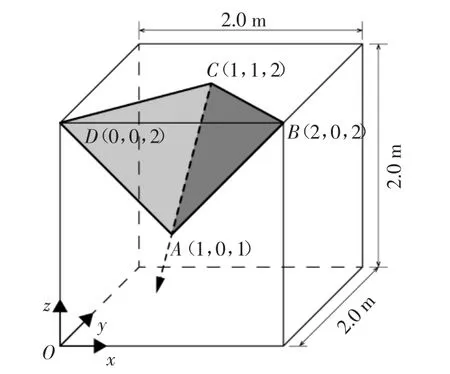
图4 块体双面滑动模型Fig.4 Model of double-plane sliding block

假设两个滑面的力学特性一致，且粘聚力均为零．滑面的摩擦角 φ 分别取为 25°、30°、35°．

首先通过块体识别程序标记可动块体，然后用本文的块体破坏数值计算程序进行计算．在每一时步都进行块体搜索，交替发生点面接触和点对接触，产生接触力．图5为计算得到的某一时刻块体变形图，块体沿滑面交线方向发生双面滑动．数值计算得到的块体位移时程与解析解比较如图6所示．可看出，数值解与解析解吻合较好，论证了该数值方法的可靠性和有效性．

采用刚体极限平衡法计算块体在双面滑动破坏下的安全系数K，可表示为[17]：

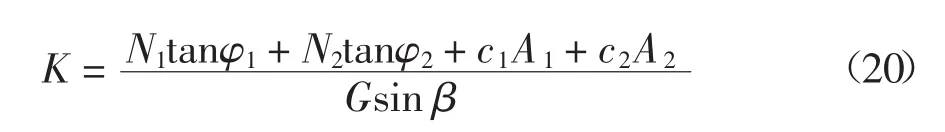
根据式（20）可求出摩擦角 φ 为 25°、30°、35°时，块体的理论安全系数分别为0.571、0.707、0.857．本数值方法采用折减滑动面强度参数求解滑块的安全系数．图7为强度折减系数与块体位移的关系曲线，可得到不同摩擦系数下块体安全系数分别为0.57、0.70和0.85．数值计算结果趋近于刚体极限平衡法结果，因此，该安全系数求解方法是可行的．

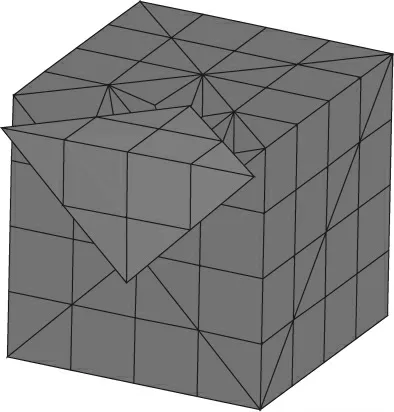
图 5 φ =25°，t=0.4 s下块体变形图Fig.5 Block deformation at t=0.4 s under φ =25°

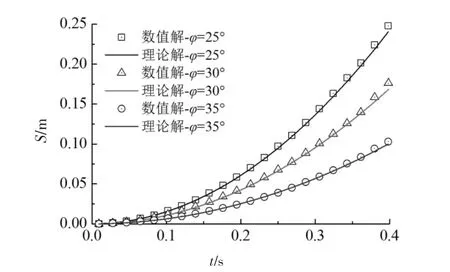
图6 滑块位移时程曲线Fig.6 Displacement time-history curves of the sliding block

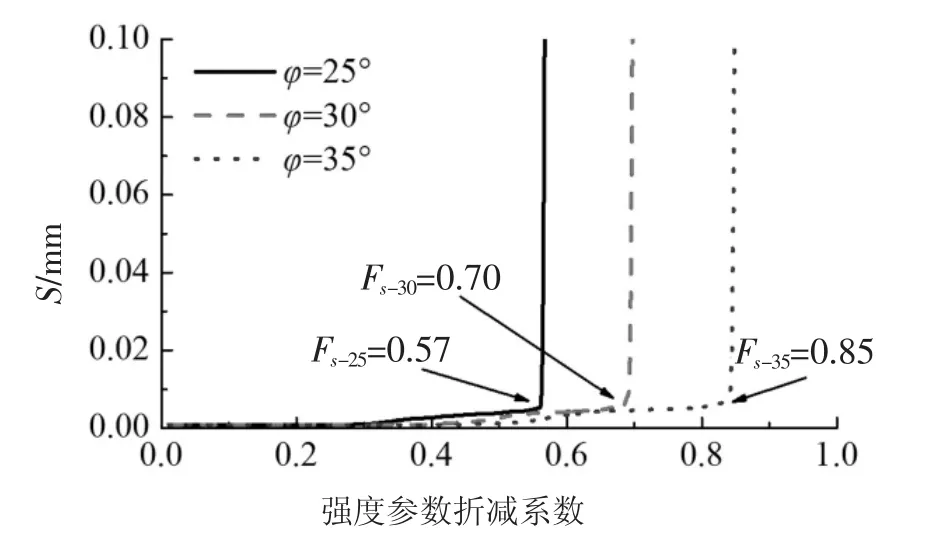
图7 强度折减系数与块体位移的关系曲线Fig.7 Displacement-reduction factor curve

5 工程实例

5.1 计算模型和计算参数

某隧洞埋深300 m．开挖断面为马蹄形，最大宽度为9.8 m，最大高度为11.2 m.隧洞附近岩体被一厚1.5 m的断层和3条较大的结构面裂隙切割.结构面位置以及计算模型的边界条件如图8所示.按照自编的块体识别程序，首先不考虑结构面，按常规方法建立网格模型；然后，采用单元重构-节点分离方法构建含结构面的网格模型；最后，通过搜索标记可动块体.如图9所示，在隧洞开挖洞周搜索到4个块体，分别标记为 B1、B2、B3、B4.可见，多组结构面互相切割后，在隧洞顶拱和左边墙容易发生块体破坏．

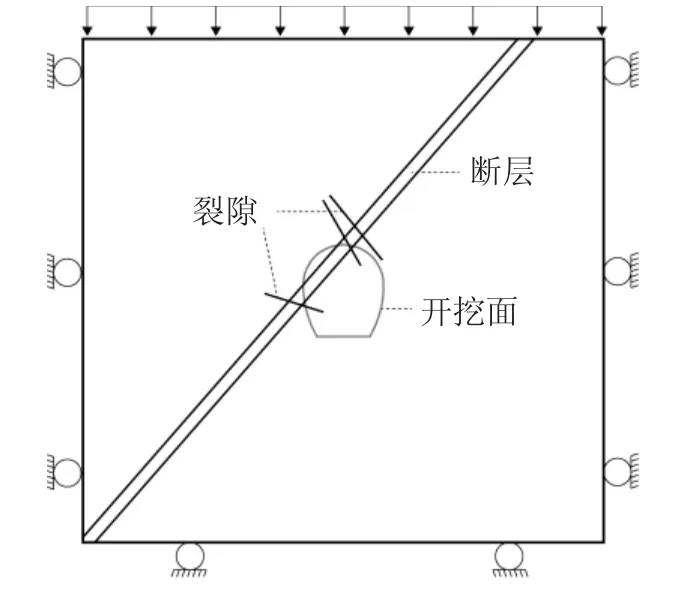
图8 计算模型示意图Fig.8 Skech of calculation model

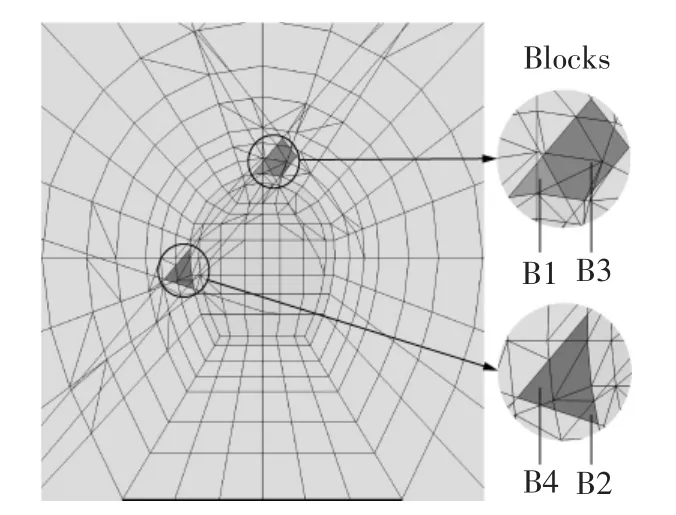
图9 重构后网格模型及标记块体Fig.9 Reconstructed FE model and marked blocks

综合分析地应力测试结果，取水平侧压力系数为1.10.隧洞区域的最大压应力在-8.5 MPa～-9.5 MPa之间.围岩以IV类为主，围岩、断层、结构面的物理力学参数取值见表1.围岩材料采用摩尔库伦准则，隧洞开挖方式为一次开挖.计算模型底部施加位移全约束，左右侧边为法向位移约束，顶部为自由边界，并施加上覆岩体产生的自重应力.得到标记块体的网格模型之后，采用本文的块体破坏数值计算程序进行计算，研究隧洞围岩和块体的变形特征，并分析块体稳定性．

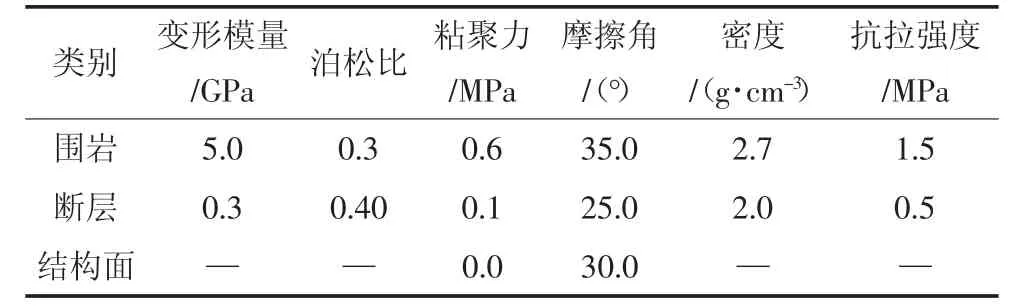
表1 物理力学参数Tab.1 Physico-mechanical parameters

5.2 结果分析

5.2.1 块体可动性和围岩位移

图10为稳定和不稳定块体的变形图，其变形量放大了5倍.图11为块体形心的位移变化过程.可看出，位于顶拱的B1块体从顶拱脱落，其位移不断增大.位于边墙的B2块体由于开挖卸荷作用，开挖后便从边墙滑落.B3、B4块体虽然是稳定块体，但在围岩和块体接触面上发生明显开裂和相对错动.从图12中的围岩变形图也可看出，断层附近岩体的变形明显较大，且断层两侧呈现非连续变形现象.左边墙断层处的相对错动距离约10 mm.块体B3、B4与围岩发生松动，是潜在的危险块体．

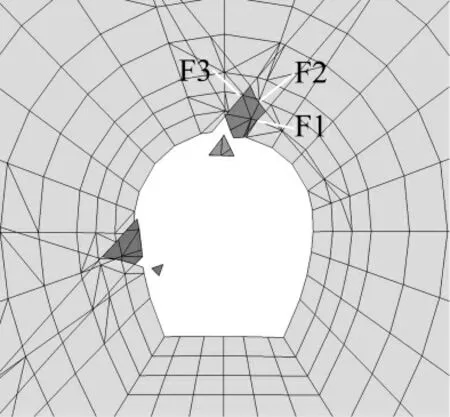
图10 稳定块体和不稳定块体（变形放大5倍）Fig.10 Unstable blocks and stable blocks（displacement amplified by 5 times）

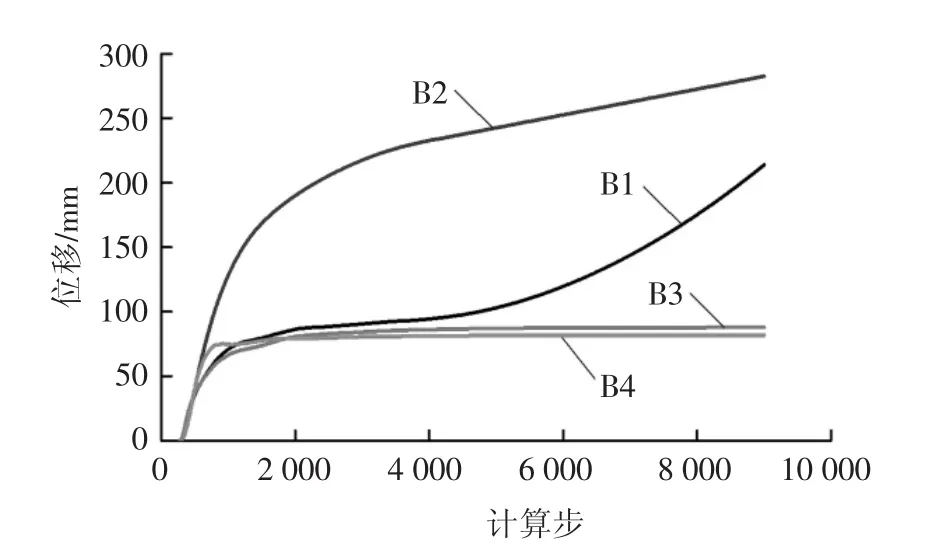
图11 块体位移曲线Fig.11 Monitored displacement of blocks

在关键块体理论中，仅能识别B1、B2块体，也无法得到围岩的位移分布特征.该数值分析方法不仅能识别关键块体，还能及时发现潜在的危险块体．

图12 围岩变形（单位：mm）Fig.12 Deformation of surrounding rock（unit：mm）

5.2.2 块体-围岩接触面的应力演化

在块体B3与围岩的3个接触面F1、F2、F3上布置3个监测点，如图10所示.提取3个监测点处的法向应力和切向应力，如图13所示.隧洞开挖后，接触面应力从4～8 MPa卸荷到0.5～1.2 MPa，并趋于某一稳定值.非滑动面F2对块体的作用力比滑动面F1更大.块体整体上受倾向于开挖面的应力作用.可见，块体在破坏过程中受来自围岩的多个结构面应力作用．

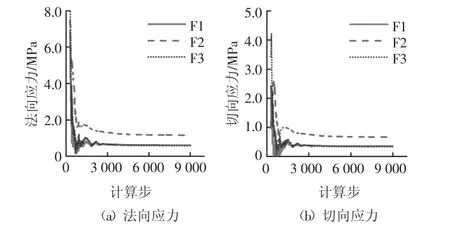
图13 块体B3与围岩接触面应力Fig.13 Stress evolution on the interfaces of Block B3

5.2.3 块体安全系数求解

对结构面参数进行折减，得到块体形心位移与强度参数折减系数的关系.当折减系数小于0.1时，块体B1、B2仍发生较大位移且计算不收敛，认为这两个块体在开挖后自由脱落.如图14所示，对于块体B3，当折减系数达到3.28时，监测点位移发生突变，故认为其安全系数为3.28.同样，块体B4的安全系数为1.79.可见，在施工中除了需要对关键块体B1、B2加强支护，还需要重点关注潜在危险块体，且该隧洞左边墙的潜在块体比顶拱的潜在块体更加危险．

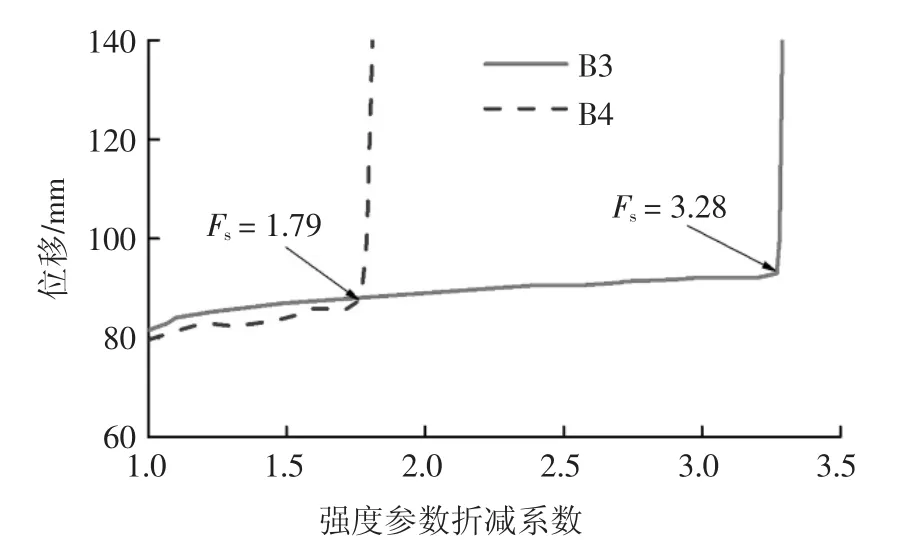
图14 块体位移与折减系数关系曲线Fig.14 Curve of block displacement and reduction factor

6 结论

1）本文提出了基于连续介质力学的块体破坏数值分析方法，考虑围岩和块体的接触作用，结合现有块体稳定分析中连续和非连续分析方法的优势，可实现同时模拟围岩的变形特性和块体的破坏过程.其在一定条件下可得到与刚体极限平衡法一致的结果.该数值方法的突出优势在于能够充分考虑开挖卸荷对块体稳定性的影响，并较好地模拟了块体和围岩发生粘结、滑移和分离多种接触状态.

2）通过对某隧洞工程的数值分析表明，受开挖卸荷的影响，关键块体发生破坏后，潜在危险块体也发生较大的变形，局部安全系数低，对隧洞施工有较大安全隐患.数值分析结果反映了围岩变形对块体稳定性的影响，模拟了复杂块体的多种破坏形态，基本规律与实际相符.该数值分析方法可为复杂地质条件下的隧洞块体稳定性提供有效的分析思路.